“不等式及其解法、线性规划、空间几何、解析几何”

■安徽省六安二中 陶兴红

一、选择题

1.若直线l1:x+(1+m)y=2-m,l2:2mx+4y+16=0互相垂直,则实数m的值为( )。

A.1或-2 B.-2

2.不等式(x-2)(2x-3)＜0的解集是( )。

A.a1a2=b1b2

B.a2b1=2a1b2

C.a1+a2=b1+b2

D.2a1+2a2=b1+b2

5.设正四面体A-BCD的棱长为2,E,F分别是BC,AD的中点,则的值为( )。

A.0≤a≤2

B.0＜a＜2

7.设x,y均为正数且2x+5y=20,则的最大值为( )。

A.1 B.2 C.10 D.20

8.如图1所示,E是正方体ABCD-A1B1C1D1的棱DD1的中点,点F,M分别在线段AC,BD1(不包含端点)上运动,则( )。

图1

A.在点F的运动过程中,存在EF∥BC1

B.在点M的运动过程中,不存在B1M⊥AE

C.四面体EMAC的体积为定值

D.四面体FA1C1B的体积不为定值

9.在平面直角坐标系中,一条双曲线经过旋转或平移所产生的一系列双曲线都具有相同的离心率和焦距,称它们为一组“共性双曲线”。例如,将等轴双曲线x2-y2=2绕原点逆时针转动45°,就会得到它的一条“共性双曲线”。根据以上材料可推理得出双曲线的焦距为( )。

10.如图2所示,已知在正方体ABCDA1B1C1D1中,F为线段BC1的中点,E为线段A1C1上的动点,则下列结论中正确的是( )。

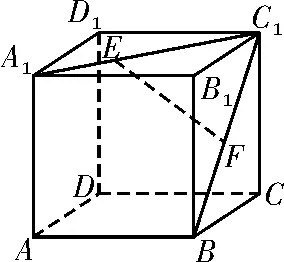
图2

A.存在点E,使EF∥BD

B.三棱锥B1-ACE的体积随动点E的变化而变化

C.直线EF与AD1所成的角不可能等于60°

D.存在点E,使EF⊥平面AB1C1D

11.某几何体的三视图如图3 所示,其中俯视图为扇形,则该几何体的体积为( )。

C.4π

D.8π

图3

12.已知正数x,y,z满足x2+y2+z2=1,则的最小值为( )。

A.3

C.4

13.(多选)已知a＞0,b＞0,a2+b2-ab=2,则下列不等式恒成立的是( )。

B.ab≤2

D.a2+b2≥4

14.(多选)已知抛物线y2=2px(p＞0)的焦点F到准线的距离为4,直线l过点F且与抛物线交于A,B两点,若M(m,2)是线段AB的中点,则( )。

A.m=1

B.p=4

C.直线l的方程为y=2x-4

D.|AB|=5

二、填空题

17.若不等式mx2+4mx-4＜0对任意实数x恒成立,则实数m的取值范围为____。

18.已知在四棱锥P-ABCD中,PA⊥平面ABCD,PA=2,底面ABCD是边长为2的正方形,用与直线PA、BD都平行的平面截此四棱锥,截面与AB、AD、PD、PC、PB分别交于F、G、H、M、E,则截面EFGHM面积的最大值为____。

19.已知直线l1:2x+y-6=0 和点A(1,-1),直线l2过点A且与直线l1相交于B,|AB|=5,则直线l2的方程为____。

20.已知关于x的不等式ax2+bx+c＞0(a,b,c∈R)的解集为{x|3＜x＜4},则的取值范围为____。

21.设M,N,P分别是棱长为2 的正方体ABCD-A1B1C1D1的棱CD,C1D1,A1B1的中点,R为BD上一点,且R不与D重合,且M,N,P,R在同一个表面积为S的球面上,记三棱锥N-MPR的体积为V,则的最小值是____。

22.如图4 所示,在正四棱锥P-ABCD中,,AB=2,从点A拉一条细绳绕过侧棱PB和PC到达D点,则细绳的最短长度为_____。

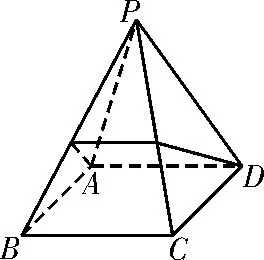
图4

23.下列命题正确的是_____。(写出所有正确命题的编号)

①命题“若a+b=0,则a=5且b=-5”的否定是“若a+b≠0,则a≠5且b≠-5”。

②已知函数f(x-1)的图像关于直线x=2对称,函数f(x)为奇函数,则4是f(x)一个周期。

③平面α⊥β,α∩β=l,过α内一点A作l的垂线m,则m⊥β。

④在△ABC中,内角A,B,C所对的边分别为a,b,c,若,则a,b,c成等差数列。

三、解答题

24.已知直线l:(2m-3)x+(m-1)y+4-2m=0(m∈R),圆C:x2+y2-6x+5=0。

(1)证明:直线l恒过定点。

(2)当直线l与圆C相切时,求m的值。

(1)求椭圆E的方程。

(2)若在椭圆E上的任一点N(x0,y0)处的切线方程是,求证:直线AB恒过定点C,并求出定点C的坐标。

(3)是否存在实数λ,使得|AC|+|BC|=λ|AC|·|BC|恒成立(C为直线AB恒过的定点)? 若存在,求出λ的值;若不存在,请说明理由。

26.如图5 所示,已知四棱锥P-ABCD的底面四边形ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=2,F为PC的中点。

图5

(1)证明:PA∥平面BDF;

(2)证明:平面PAC⊥平面BDF;

(3)求三棱锥P-BDF的体积。

27.已知不等式mx2-2x-m+1＜0。

(1)若对所有的实数x使得不等式恒成立,求m的取值范围;

(2)设不等式对于满足|m|≤2的一切m的值都成立,求x的取值范围。

28.如图6所示,在几何体ABCDEGF中,四边形ABCD为菱形,AG∥BF∥DE。

图6

(1)证明:GF∥平面EDC;

(2)若BF=DE=2AG=4,AB=4,,AG⊥平面ABCD,求二面角G-EF-C的余弦值。

29.在平面直角坐标系xOy中,P(x0,y0)(y0≠0)是椭圆C上的点,过点P的直线的方程为。

(1)求椭圆C的离心率;

(2)当λ=1时,设直线l与x轴,y轴分别交于A,B两点,求△OAB面积的最小值;

(3)设椭圆C的左焦点和右焦点分别为F1,F2,点Q与点F1关于直线l对称,求证:Q,P,F2三点共线。

30.如图7 所示,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD。

图7

(1)求证:PC⊥BD。

(2)过直线BD且垂直于直线PC的平面交PC于点E,当三棱锥EBCD的体积取到最大值时,求:

①PA的长度;

②二面角A-DE-B的余弦值的大小。

参考答案：

一、选择题

1.D 2.C 3.A 4.A 5.A 6.D

7.A 8.C 9.C 10.D 11.C 12.C

13.BC 14.BC

二、填空题

23.②④

三、解答题

24.(1)将直线l的方程整理得(2x+y-2)m+(-3x-y+4)=0。

(2)将圆C的一般方程化成标准方程为(x-3)2+y2=4,所以圆C的圆心为(3,0),半径为2。

因为直线l与圆C相切,所以圆心C到直线l的距离等于半径。

26.(1)如图8,连接AC交BD于点O,连接OF。因为F为PC的中点,所以OF为△PAC的中位线,所以OF∥PA。又因为OF⊂平面BDF,PA⊂平面BDF,所以PA∥平面BDF。

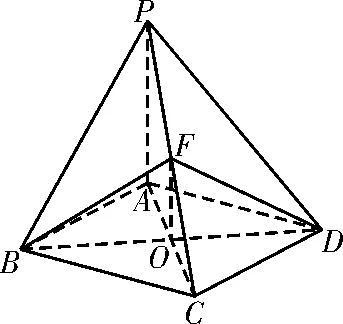
图8

(2)因为PA⊥平面ABCD,AC⊂平面ABCD,所以PA⊥AC。因为F为PC的中点,所以OF∥PA,所以OF⊥AC。因为底面ABCD是菱形,所以AC⊥BD。又OF∩BD=O,所以AC⊥平面BDF。因为AC⊂平面PAC,所以平面PAC⊥平面BDF。

27.(1)当m=0时,-2x+1＜0,对所有的x不恒成立。

当m≠0时,设f(x)=mx2-2x-m+1,若f(x)＜0对所有的实数x恒成立,则需二次函数y=f(x)的图像全在x轴的下方,所以m＜0,且Δ=4-4m(1-m)＜0,无解。

综上可得,不存在这样的m,使得不等式mx2-2x-m+1＜0恒成立。

28.(1)因为AG∥DE,AG⊄平面EDC,DE⊆平面EDC,所以AG∥平面EDC。因为四边形ABCD为菱形,所以AB∥DC。同理可得AB∥平面EDC。又因为AB∩AG=A,所以平面ABFG∥平面DCE。因为GF⊆平面ABFG,所以GF∥平面EDC。

(2)连接AC,BD相交于点О,以OA,OB分别为x轴,y轴,建立如图9所示的空间直角坐标系O-xyz。

图9

由图知二面角G-EF-C的平面角为钝角,所以其余弦值为。

①若x0=0,则P(0,λ),Q(-λ,2λ),此时kF2P=-1,kF2Q=-1,因为kF2Q=kF2P,所以Q,P,F2三点共线。

当点P的坐标为(0,-λ)时,也满足。

②若x0≠0,设Q(m,n),m≠-λ,F1Q的中点为M,则,代入直线l的方程得x0m+2y0n-x0λ-4λ2=0。

因为kF2Q=kF2P,所以Q,P,F2三点共线。

综上可得,Q,P,F2三点共线。

30.(1)连接AC,因为四边形ABCD是正方形,所以BD⊥AC。因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD。又AC∩PA=A,所以BD⊥平面PAC。又PC⊂平面PAC,所以PC⊥BD。

②以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图10所示的空间直角坐标系A-xyz,则A(0,0,0),C(1,1,0),D(0,1,0),)。

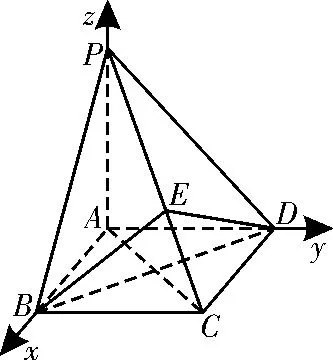
图10

因为二面角A-DE-B为锐角,所以二面角A-DE-B的余弦值的大小为。