似然函数形式对水稻物候期模型品种参数校正的影响

杨 华，姜海燕 ，赵空暖，钱峥远

（南京农业大学人工智能学院，南京 210095）

0 引言

作物生长模拟模型（以下简称“作物模型”）是作物精确栽培技术研究的重要工具，可以动态模拟不同品种在生长发育生理过程中与环境变量间的定量关系[1]。由于建模人员对作物生理生态过程认识不足，无法考虑全部的限制因子，导致模型存在一定的不确定性[2]，会使使用者对模型预测结果不信任并影响应用效果[3]。这一因素限制了作物模型的大规模推广，因此在应用时有必要进行不确定性优化。按照来源，作物模型的不确定性可分为结构不确定性、参数取值不确定性、数据不确定性以及主观的不确定性[4-5]。模型不确定性优化方法亦是围绕上述几个方面展开，主要分为参数不确定性优化、模型结构不确定性优化及综合的不确定性优化[6]。其中参数不确定性优化是作物生长模型应用的核心环节。作物模型参数主要是指品种参数，虽然模型自身提供了参数的参考值，但部分参数随生态点地理位置及作物品种等变化而变化[7]，因此，在应用模型时先要对这部分参数进行优化并验证，提升其在某一地区的适用性。

校正作物模型品种参数的常用方法是基于统计理论的，主要包括广义似然不确定性估计（generalized likelihood uncertainty estimation，GLUE）方法和马尔科夫链蒙特卡罗（Markov chain Monte Carlo，MCMC）方法[8-9]。GLUE 方法存在计算时消耗资源过大，运行周期较长的问题，而且只考虑了参数的先验分布，未将样本信息先验分布以似然函数（likelihood function，LF）形式化，这可能低估了模型的不确定性，导致参数校正结果及不确定度（uncertainty ratio，UR）分析时造成偏差[10]。而MCMC 方法充分利用了样本信息先验分布，并将其用LF 表示，结合参数先验信息，以概率密度核函数的形式来表示模型参数分布[11]，并能够量化参数不确定性，因此成为不确定条件下作物模型参数校正的主流方法。黄健熙等[12-13]利用MCMC 对WOFOST、ORYZA 系列等模型进行参数标定，均取得良好效果。WALLACH 等[14-17]采用MCMC 进行模型不确定性量化和分析，为模型本地化应用提供参考，TAN 等[18]初步比较了GLUE 和MCMC 方法对参数校正结果的影响，发现MCMC 方法一定程度上优于GLUE。

利用MCMC 方法对模型参数校正的关键是LF 形式设计，LF 代表了模型残差的分布特点，大部分作物模型研究中都是将LF 设为高斯正态似然函数（gaussian likelihood function，GLF）形式[19]，GLF 要求模型残差的方差恒定，然而作物模型残差具有异方差性，即模型在可控制变量条件下具有变化的方差，这种变化的方差是由观测数据的不确定性和模型本身的复杂性造成的[20]。有研究表明，在农业观测数据中，由于测量手段、测量人员主观性和环境因素影响，关键物候期和产量等测量值随年份变化而波动较大，会导致模型残差平稳性较差和离散程度较大，从而导致异方差性[21]。这会给参数校正的结果带来偏差，影响作物模型的应用。

本研究以RiceGrow 和Oryza2000 水稻物侯期模型为研究对象，以中国南方地区早、中、晚3 种不同熟性的水稻品种栽培试验数据为基础，通过引入变异系数（coefficient of variation，CV）变换的高斯似然函（GLF with CV transformation，GLF-CV）和引入BC（Box-Cox）变换的高斯似然函数（GLF with BC transformation，GLFBC）对观测数据和模型结构造成的异方差进行特征描述，并以参数后验分布UR 和模型预测UR 为评价标准进行不同LF 下参数校正结果比较，以期为利用MCMC 方法进行水稻生长模型参数校正的LF 选择提供参考，同时也为作物生长模型本地化应用提供指导。

1 材料与方法

1.1 站点数据

研究数据集选取中国广东省肇庆市高要区2004—2009 年、江苏省泰州市兴化市2001—2004 年、安徽省六安市1991—2004 年3 个南方地区水稻种植生态点的早熟（雪花粘）、中熟（武育粳3 号）、晚熟（汕优63 号）水稻品种各年份的田间试验资料，品种和栽培信息见表1。其中，雪花粘的播种期范围为3 月7—13 日，成熟期范围为7 月8—15 日左右；武育粳3 号播种期范围为5 月4—13 日左右，成熟期范围为10 月8—15 日左右；汕优63 号播种期范围为4 月18—25 日左右，成熟期范围为9 月3—15 日左右。

表1 不同熟性水稻品种种植地点和年份Table 1 Planting place and year of rice varieties with different maturity

气象数据来源：高要、兴化、六安3 个地点各年份气象数据均来源于国家气象局气象中心，基础气象数据包括日最高温度（℃）、日最低温度（℃），日照时数（h/d）和降雨量（mm）。

1.2 模型品种参数

研究采用2 个非线性程度不同的物侯期模拟模型，分别是由南京农业大学国家信息农业工程技术中心研制的RiceGrow 物候期模型[22]和由国际水稻研究所及荷兰瓦格宁根大学联合开发的Oryza2000 物候期模型[23-24]。各模型敏感性品种参数描述及范围如表2 所示。

1.3 模型参数校正方法

1.3.1 贝叶斯统计推断

对于水稻物侯期模型的驱动数据、模型品种参数和模型输出，公式描述为

其中yi代表模型第i个试验输出关键物候期（如拔节期、成熟期等）儒历天数（confucian calendar days，CCD）。为第i个驱动数据，如气象数据、土壤数据和田间管理数据等，θ为模型品种参数，εi为模型残差，根据贝叶斯公式，模型参数的后验分布为

式中p(yi|θ,xi)为模型残差εi先验分布。本研究中用实际关键物候期与模型模拟值CCD 之间差值的LF 表示，p(θ)为模型参数θ的先验分布。

1.3.2 MCMC 参数校正框架

在作物模型领域，MCMC 方法是基于贝叶斯推理的参数后验分布估计中最有效的方法。该方法进行模型参数估算的基本思想是产生1 个马尔科夫链，以目标分布为平稳分布，目标分布一般为p(yi|θ,xi)，根据马尔科夫理论，1 个马尔科夫链从任意初值出发，都会收敛到平稳分布。MCMC 方法的目的是在构造1 个马尔可夫链的基础上生成参数集的样本，通过参数集的平稳分布即可求出每个参数的后验分布[25]。框架见图1。首先设定品种参数先验分布、模型约束目标变量残差的LF 和MCMC采样算法，从参数先验分布中选择参数值进行初始化，初始化值确定依据具体的MCMC 采样算法而定。在田间管理数据、土壤数据和气象数据等驱动下，运行生长模型得到约束目标变量值，将此值与LF 进行符合程度比较，并依据符合程度构造参数的马尔科夫链，经过蒙特卡罗采样，获取新的参数值，重新代入模型运行，依次循环，当达到马尔科夫收敛条件或设置的指定马尔科夫链个数时，停止计算，此时获得参数的后验分布。

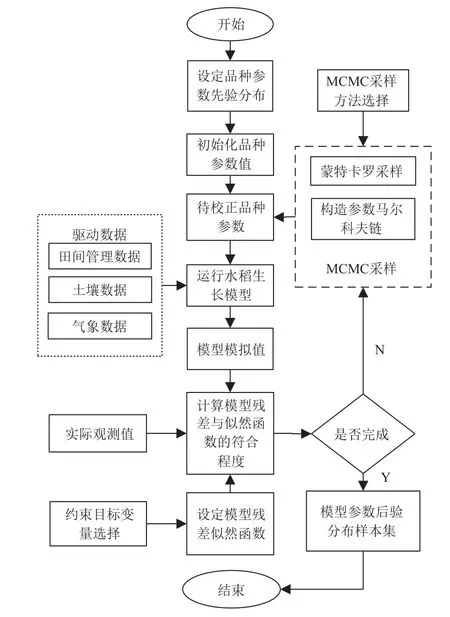
图1 基于MCMC 方法的作物模型参数校正框架Fig.1 Parameter correction framework of crop model based on Markov chain Monte Carlo (MCMC) method

1.3.3 品种参数先验分布

模型参数的先验分布对用MCMC 方法进行参数后验分布估计影响不大，一般设为均匀分布，参数先验均匀分布的范围见表2。

1.3.4 模型残差先验分布

模型残差是模型模拟值和实测值之间的差值，从统计学的角度来看其服从一定的先验分布。模型残差的先验分布可用概率密度函数来表示，概率密度函数是一种关于模型残差特征的假设，而LF 是以概率密度函数中各参数为变量的函数，MCMC 方法通过不断采样模型参数值，使模型残差的分布符合这个LF，因此LF 的形式对参数校正的结果影响较大，关于LF 形式的讨论具体见1.4。

1.3.5 约束目标变量

由于不同模型在物候期模拟上存在一定差异，且不同水稻品种的物候期试验数据在年份上不完全相同，因此，RiceGrow 物候期模型中，雪花粘品种选择出苗、拔节期、抽穗期和成熟期作为目标变量，武育粳3 号品种选择拔节期、抽穗期和成熟期作为目标变量，汕优63 号品种选择出苗、拔节期、抽穗期和成熟期作为目标变量；在Oryza2000 物候期模型中，3 个品种均选择孕穗期、抽穗期和成熟期作为目标变量。

1.3.6 MCMC 采样方法

研究采用仿射不变马尔科夫链蒙特卡洛集成采样算法（ensemble sampling for affine-invariant MCMC，EMCEE），该算法由GOODMAN 提出，并由FOREMAN等用python 工具实现[26]。它引入了仿射不变性采样器，相对于传统的MCMC 方法能产生更多的独立样本，自相关时间更短，且利用多个CPU 内核，提高了计算并行性。目前已经在Nature 和Science 等期刊上有关天体物理学文献中被使用[27-28]，但是还未被应用于作物模型中。源码见https://github.com/dfm/emcee。

在EMCEE 算法中，有以下参数需要设置：

1）参数维度。依据模型参数而定，本研究中RiceGrow 与Oryza2000 物候期模型带校正品种参数均为5 个，参数维度设置为5。

2）并行马尔科夫链初始条数。EMCEE 算法采用多条并行马尔科夫链进行采样，并行的马尔科夫链初始条数一般是参数维度的4～6 倍[27]，本研究中取6 倍，即30。

3）参数初始值。1 条马尔科夫链需要1 组参数值，品种参数初始值的维度等于初始马尔科夫链条数，依据步骤2），本研究中取30。每1 组的参数初始值由参数先验分布区间上均匀采样而来。

4）马尔科夫链长度。马尔科夫链长度为初始马尔科夫链达到稳定时的条数，在EMCEE 算法中作为收敛条件，一般依据经验设定，本研究中设为1 000。

1.4 LF 形式

1.4.1 GLF

GLF 不考虑模型残差的异方差性，其分布服从均值为0，方差为常数的正态高斯分布。并可用概率密度函数表示为

式中σ为标准差，各关键物候服从以观测日期CCD 为期望的高斯分布。为了使值稳定、函数形式简单、计算方便，所有概率密度的计算均通过取对数形式计算。模型残差εi为

各关键物候期观测值联合GLF 为

式中n为关键物侯期个数，是第i个关键物侯期儒历天数模型模拟值，Si是第i个关键物侯期儒历天数模型模拟值，Oi是第i个关键物侯期儒历天数观测值。本研究中标准差σ取Oi的1%。

1.4.2 GLF-CV

在实际物侯期观测中，即使观测方法和观测设备相同，不同水稻品种历年关键物候期观测值的方差也并不恒定，这是模型残差异方差性重要来源之一。

本研究中，汕优63 号品种成熟期的观测数据出现较多异常值，且中位数分布在上、下四分位数之外，说明该物候期观测数据离散程度较大。受不同年份季节气候的影响，同一水稻品种关键物侯期观测值的方差和均值随年份变化而变化，因此在使用GLF 时可能存在偏差。

平稳性和离散程度是数据异方差性是否存在的直接反映，一般用变异系数CV 表示，虽然水稻物候期观测数据的方差会随年份变化，但方差和均值的比值在理想情况下应该接近恒定的值[29]，本研究引入CV 来对模型残差的异方差性进行修正。CV 定义为方差和均值的比值，可得修正后的各关键物候期联合GLF-CV：

CV 根据每个关键物候期的历年观测值确定，将观测值变化的方差转为恒定的CV 值与均值的乘积，一定程度上达到修正模型残差异方差性的作用。

1.4.3 GLF-BC

水稻物候期模型的非线性、不连续、非凸的特点[6]也是模型残差异方差性的重要来源。为了同时考虑模型结构和观测数据带来的异方差性，本研究引入GLF-BC进行改善。

GLF-BC 的思想是BC 变换，它是统计学中一种通过数学变换手段改善数据异方差性的有效方法，主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，通过BC 变换可以将模型残差转化为独立相同分布的特性[30]。BC 变换的一般形式为

式中λ是变换参数，y是模型模拟或观察到的结果。经过BC 变换后，模型的残差表示为

将式（5）中的εi替换为式（9），可得各关键物候期观测值联合GLF-BC 为

当λ=1 时，BC 变换无效，即模型残差无变换，当λ=0 时，BC 变换为对数变换，而通过观测值确定时常常结果在接近边界（通常靠近1）[31]，因此为了使BC 变换有效同时方便计算，本研究中使用BC 变换中的平方根转换，即取λ=0.5。

1.5 试验环境与设计

1.5.1 试验环境

物侯期预测模型程序均为用Java 语言自主开发具有Restful 风格的web 服务，主体算法程序使用python 语言开发，采样算法使用EMCEE 工具包，试验运行环境是Intel（R）Xeon（R）Platinum8163CPU@2.50 GHz，内存16 GB，Windows10 64 位操作系统。

1.5.2 试验设计

设计了两组试验分析比较了不同LF 对用MCMC 方法进行模型参数校正的影响。数据源为3 个水稻品种历年站点数据（表1），模型包括RiceGrow 和Oryza2000物候期模型。LF 分别为GLF、GLF-CV 和GLF-BC，结果分别对校正后的模型参数后验分布、模型参数UR 和模型预测UR 进行比较。其中，GLF-CV 是在GLF 基础上改善了σ，使观测数据方差趋于稳定，GLF-BC 在GLF 基础上同时改善了σ和εi，从降低模型结构非线性造成的异方差进行修正。

1.5.3 试验评价指标

评价方法包括参数校正后验分布、参数UR 和模型预测UR 评价。

参数后验分布用概率密度核函数图表示，由多组参数向量通过曲线拟合而成。

参数属于无量纲的值，参数UR 是一种参数校正结果可信赖程度的量化指标，用均方根偏差（root mean square deviation，RMSD）和相对均方根偏差（relative root mean square deviation，RRMSD）表示[32]，

式中p为后验分布中参数集个数，θi表示第i个参数，为参数集均值。当θ服从高斯分布时，RMSD 可以作为总标准差的无偏估计。为了比较不同参数集的离散程度和稳定性，计算参数后验分布的RRMSD，计算式为

模型预测UR 用均方根误差（root mean square error，RMSE）、标准均方根误差（normalized root mean square error，NRMSE）来表示。

式中q为关键物侯期个数。

2 结果与分析

2.1 参数校正结果比较

2.1.1 RiceGrow 物候期模型参数后验分布与UR 比较

1）参数后验分布比较

GLF、GLF-BC 和GLF-CV 下RiceGrow 物侯期模型雪花粘、武育粳3 号、汕优63 号品种参数后验分布的概率密度核函数图见图2。可以看出参数后验分布收敛区间相对于先验分布均有缩小，3 种LF 在RiceGrow 物候期模型参数校正均有一定的效果。

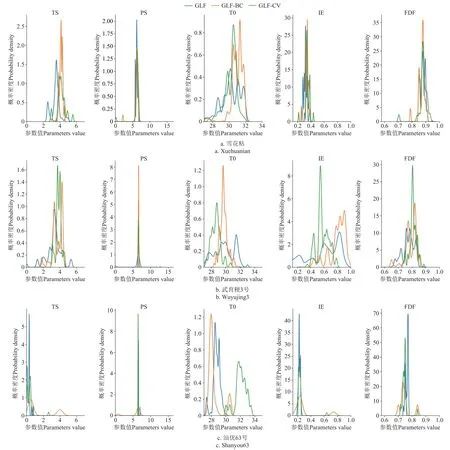
图2 不同似然函数下RiceGrow 物候期模型参数后验分布概率密度核函数图Fig.2 Posterior distribution probability density kernel function of RiceGrow phenological model parameters under different likelihood functions

品种参数TS、FDF、To、IE 与品种熟性无明显关系，PS 代表了水稻的感光性，PS 值越高代表感光性越强，一般来说早熟品种基本不感光或感光极弱，晚熟品种感光较强，而中熟品种感光性较复杂，雪花粘、武育粳3 号、汕优63 号分别对应早熟、中熟和晚熟品种。由图2 可以看出，3 种LF 下雪花粘PS 概率密度函数峰值对应的参数值均小于汕优63 号，这与实际较为吻合。在汕优63 号中，GLF-BC 下PS 概率密度函数的区间较GLF-CV 和GLF 更为收敛，表明GLF-BC 下得出的PS后验分布更为精确。

2）参数UR 比较

由表3 可以看出，GLF-BC 所得的各种参数RRMSD最小，其次是GLF-CV，GLF 表现最不理想。这是因为而GLF-CV 只考虑观测数据带来的异方差，未考虑模型结构带来的异方差，GLF-BC 同时考虑了这两种异方差的来源，因此GLF-BC 下的参数RRMSD 小于GLF-CV，GLF-CV 小于GLF，这表明了GLF-BC 和GLF-CV 在改善残差异方差性上具有一定的作用，也从反面证明了RiceGrow 物候期模型的异方差性与模型结构本身有关。

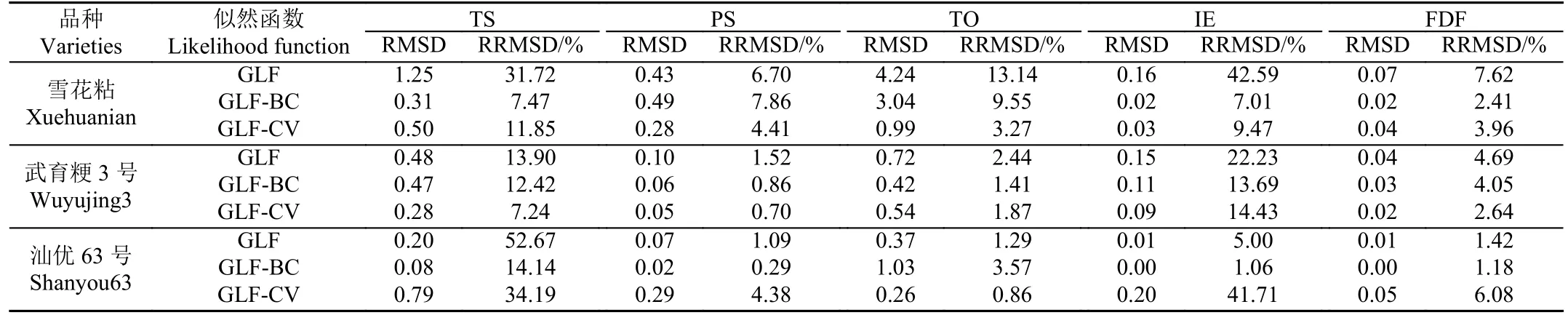
表3 不同似然函数下RiceGrow 物候期模型参数不确定度Table 3 Uncertainty ratio of RiceGrow phenological model parameters under different likelihood functions

2.1.2 Oryza2000 物候期模型参数后验分布与UR 比较

1）参数后验分布比较

3 种LF 下Oryza2000 物侯期模型参数后验概率密度核函数图见图3，品种参数DVRJ、DVRP、DVRR、PPSE与品种熟性无明显关系，DVRI 是水稻感光性的倒数，DVRI 值越小代表感光性越强，图中可以看出3 种LF 下雪花粘DVRI 概率密度函数峰值对应的参数值均大于汕优63 号，这与实际较为吻合。在汕优63 号中，GLFBC 下DVRI 概率密度函数的区间较GLF-CV 和GLF 更为收敛，且峰值对应的参数值更小，表明GLF-BC 下得出的DVRI 后验分布更为精确。

图3 不同似然函数下Oryza2000 物候期模型参数后验分布概率密度核函数图Fig.3 Posterior distribution probability density kernel function of Oryza2000 phenological model parameters under different likelihood functions

2）模型参数UR 比较

由表4 可知，GLF 所得的雪花粘品种参数RRMSD最小，GLF-BC 所得的汕优63 号品种参数RRMSD 最小；GLF-CV 所得的武育粳3 号品种参数RRMSD 最小，3 种LF 所得的各品种参数RRMSD 均有差别。这可能是因为汕优63 号品种的观测数据年份最长（见表1），根据统计学理论观点，观测数据越多，其数据特征越趋于稳定，GLF-CV 的假设即是观测数据具有固定的变异系数，这与观测数据具有稳定性是一致的。同时由于在RiceGrow物候期模型利用二次曲线函数来描述每日光周期效应，Beta 函数描述每日热效应，这两种函数均是非线性函数，而Oryza2000 物候期模型结构采用多个线性函数进行级联，其非线性较RiceGrow 弱。若其异方差大部分来源于模型结构，GLF-BC 好于GLF-CV 是有可能的。若观测数据的异方差性整体较小且Oryza2000 模型非线性较弱，GLF 好于GLF-CV、GLF-BC 也是有可能的。

2.2 模型预测UR 比较

将参数后验分布中的均值带入模型运行得到模拟结果与观测值进行比较分析。在RiceGrow 物侯期模型中，选取出苗期、拔节期、抽穗期、成熟期4 个关键物候期进行比较；在Oryza2000 物侯期模型中，选取孕穗期、抽穗期、成熟期3 个关键物候期进行比较。结果见表5。

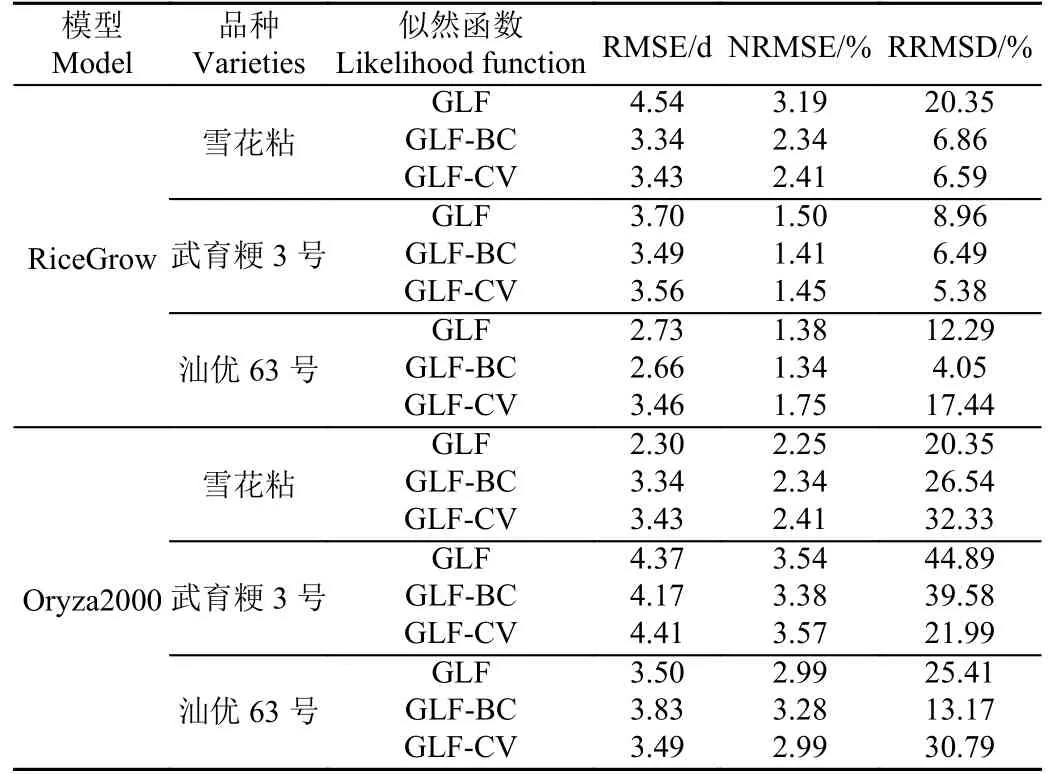
表5 不同似然函数下2 种物候期模型预测UR 及参数UR 比较Table 5 Comparison of two phenophase models for predicting uncertainty ratio and parameters uncertainty ratio under different likelihood functions

GLF-BC 下雪花粘、武育粳3 号、汕优63 号品种的RiceGrow 物候期模型预测RMSE 为3.34、3.49、2.66 d；整体上均小于GLF-CV 下的3.43、3.56、3.46 d 和GLF 下的4.54、3.70、2.73 d，这与前一节得出的参数UR 中GLFBC 小于GLF-CV 和GLF 对应，说明了在RiceGrow 物候期模型中，参数RRMSD 越小，模型预测RMSE 越小，整体上GLF-BC 表现最好，GLF-CV 其次，GLF 最后。

雪花粘、武育粳3 号、汕优63 号品种的Oryza2000物候期模型预测RMSE 最小的分别是GLF、GLF-BC、GLF-CV，并没有像RiceGrow 物候期模型中出现GLFBC 一直表现良好的现象，这是因为LF 可以看作是一种描述模型预测UR 的方法，而模型预测UR 来源包括模型结构UR、模型参数UR、观测数据UR 等，不同的LF 体现的各类UR 来源权重不同，对模型的匹配程度也不尽相同，相对于RiceGrow，Oryza2000 物候期模型的结构非线性程度和复杂性较低，对于参数校正而言，观测数据UR 对模型预测UR 的影响较大，而不同品种和年份的观测数据存在一定差异，因此在Oryza2000 物候期模型中，LF 对于不同品种参数校正的适应性不同。

取每个LF 下的所有品种的参数RRMSD 和模型预测RMSE 的值，得到参数整体UR 和模型预测UR 的量化关系，从表5 可以看出，在RiceGrow 物候期模型中，整体上，参数RRMSD 越小，模型预测RMSE 越小，这可能是因为其参数UR 是模型预测UR 的主要来源。而在Oryza2000 物候期模型中，GLF 的模型预测RMSE 最小，但其参数RRMSD 却最大，模型预测的UR 并未随着参数UR 同方向变化，这可能是因为其模型参数UR占据模型预测UR 的来源权重较小。

对比两种模型结构，在揭示水稻发育进程的规律中，Oryza2000 物候期模型对于光周期效应和热效应的描述均采用线性方程，相对于RiceGrow 更为简化，因此同样的观测数据，在Oryza2000 中对于参数校正结果的影响较大，因此其观测数据UR 可能占据模型预测UR 的来源权重较大。而参数UR 对模型预测UR 的影响，只有在参数UR 占据主要来源权重时，才会呈同趋势变化。

3 讨论

在RiceGrow 物候期模型中，用MCMC 方法进行参数校正时，GLF-BC 好于 GLF 和 GLF-CV，然而Oryza2000 物候期模型中不同LF 的效果更依赖于观测数据，从模型结构来看，这是由于Oryza2000 物候期模型的线性程度较RiceGrow 高。引入GLF-BC 和GLF-CV的目的是为了改善模型残差的方差特征，使模型残差符合正态高斯分布，这对非线性系统模型来说是有一定效果的，在线性系统模型中，模型残差一般均为随机误差，且符合正态高斯分布，一般不需要进行变换。因此将GLF-BC 和GLF-CV 用于MCMC 方法进行Oryza2000 物候期模型参数校正和不确定性分析效果可能不明显，这需要更多的试验进行验证。

在GLF-BC 中，本文假设的BC 变换系数值取值为1/2，这是参考一般的BC 均值变换，虽然在RiceGrow物候期模型中效果良好，但是若在MCMC 采样过程中能够结合观测数据动态调整，将进一步提高LF 的适用性，比如在Oryza2000 物候期模型中使用自适应的LF，这是下一步将要研究的问题。

模型结构UR、参数UR 和观测数据UR 是模型预测UR 的重要来源，本研究初步量化了参数UR 与预测UR 的关系，但并未对模型结构UR、观测数据UR 与模型预测UR 的关系进行量化，这是下一步的工作。

4 结论

本研究通过引入引入变异系数（coefficient of variation，CV）变换的高斯似然函数（Gaussian likelihood function with CV transformation，GLF-CV）和 BC（Box-Cox）变换的高斯似然函数（GLF with BC transformation，GLF-BC）对水稻物候期模型残差的异方差性进行修正，以RiceGrow 和Oryza2000 物候期模型为研究对象，通过试验对比了3 种似然函数（likelihood function，LF）下用马尔科夫链蒙特卡洛（Markov chain Monte Carlo，MCMC）算法进行雪花粘、武育粳3 号、汕优63 号水稻品种参数校正和不确定性量化分析结果。得出主要结论如下：

1）引入的GLF-BC 和GLF-CV 在用MCMC 方法进行水稻物候期模型参数校正时均有效果，得出的雪花粘、武育粳3 号、汕优63 号参数后验分布均值带入RiceGrow和Oryza2000 进行模型预测，均方根误差范围分别为2.66～4.54、2.30～4.41 d。

2）在RiceGrow 物候期模型中，3 个水稻品种参数相对均方根偏差RRMSD（relative root mean square deviation，RRMSD）和模型预测均方根误差（root mean square error，RMSE）均是GLF-BC 最小，在GLFBC 下模型预测 RMSE 比 GLF-CV 小 0.09、0.07、0.80 d，比GLF 小1.21、0.20、0.07 d，表明GLF-BC 对 RiceGrow物候期模型具有良好的适应性。在Oryza2000 物候期模型中，雪花粘、武育粳3 号、汕优63 号3 个水稻品种的模型预测RMSE 最小的是GLF、GLF-BC 和GLF-CV，分别为2.30、4.17、3.50 d，3 种LF 各有优势。

3）初步量化了不同LF 下模型预测不确定度（uncertainty ratio，UR）和参数UR 之间的关系。在RiceGrow 物候期模型中，参数UR 是模型预测UR 的主要来源，在Oryza2000 物候期模型中，观测数据UR 可能是模型预测UR 的主要来源。MCMC 通过对采样得到的参数进行统计分析，估计模型参数的后验分布，后验分布反映了参数UR。而LF 在参数校正中起到了关键的作用，参数后验分布的形状和位置受LF 的影响，因此LF 的选择和定义可能因具体问题而异，需要能够与模型和观测数据的特性相匹配。LF 的选择与模型残差异方差的主要来源有关，当主要来源为观测数据时，GLF-CV好于其他；当主要来源为模型结构本身时，GLF-BC 好于其他；当模型残差的异方差性较小时，可使用GLF。