颗粒体积浓度对半开式叶轮离心泵泄漏涡和磨损的影响

2023-11-26柳涵宇王李科卢金玲

农业工程学报 2023年16期

王凯，柳涵宇，王李科，卢金玲

（西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048）

0 引言

与闭式叶轮离心泵相比，半开式叶轮以其结构简单紧凑、维护方便、便于输送黏性较大流体等优点，在石油化工、水利工程等领域越来越受到青睐[1]。但是，叶片与泵体形成的叶顶间隙会导致在叶片压力面和吸力面压差的作用下产生流动分离、二次流和脱流等不稳定流动，使泵内流动损耗较高[2-4]。中国河流含沙量较大，离心泵长期运行于此类泥沙浓度较大的流体环境中时，水中的固体颗粒会对过流部件产生撞击和切削，使过流表面产生变形，发生磨损破坏，导致机组运行稳定性变差，效率降低[5-7]。

目前国内外研究学者对颗粒浓度对水力机械的磨损速率的影响进行了大量的研究。LEI 等[8]基于SST 湍流模型，结合欧拉-拉格朗日方法模拟泵内泥沙颗粒的运动轨迹和磨损机理，从而建立颗粒参数与泵性能及转轮叶片磨损情况的关联。SHEN 等[9]基于欧拉-拉格朗日的离散相模型，模拟了不同固相质量浓度工况下的螺杆离心泵内部流场，分析了固相颗粒的能量变化、轨迹特征及磨蚀规律。LAI 等[10]采用双向耦合欧拉-拉格朗日方法对离心泵进行磨蚀计算并预测磨蚀机制，得到了过流部件磨损严重的区域分布。张自超等[11-12]考虑相间阻力和泥沙扩散系数两方面的影响，基于改进的Euler-Euler 算法对双吸离心泵流场进行数值模拟，得出湍流强度和颗粒动态尺度对磨损严重的块状磨损区分布。张玉良等[13]基于代数滑移混合物模型对离心泵内部流场进行定常流动数值计算，发现在靠近隔舌的叶轮出口处的三种速度组合的双剪切层射流-尾流结构和固相体积分数对叶片表面的磨损程度影响。汪家琼等[14]基于Particle 模型和非均相模型，分析了离心泵过流部件壁面处固体颗粒体积浓度与磨损程度间的关系。周世杰等[15]基于相关试验改进了固相粒子动量方程，结合Alert 磨损经验公式对抽黄用泵进行数值模拟计算和分析，固相体积浓度递增加剧了叶轮进口回流现象和部件表面磨损程度。

半开式叶轮叶顶间隙泄漏流研究方面，张青扬等[16]对半开式叶轮离心泵进行全流道数值模拟，发现叶顶间隙影响叶轮流道中的压力分布，产生的回流、涡流、扰流等不稳定流动严重影响泵内部流场性能参数。AYAD等[17]通过数值模拟研究发现不同流速条件下，发现不同流量工况下离心泵扬程和效率的变化与叶顶间隙变化量近似为回归效应，增加叶顶间隙宽度，二次流产生的涡旋会阻碍核心流动。MOUSMOULIS 等[18]采用了一种齐次方法分别对半开式径向叶轮离心泵在两相条件下进行数值模拟，分析了叶顶间隙区域与叶轮回流和靠近叶片前缘的二次流间的关联性。贾晓奇等[19]对不同工况下半开式叶轮离心泵内部三维湍流流场进行数值模拟，揭示了不同流量工况下叶顶间隙泄漏涡的流动特性、叶顶间隙总压与相对速度分布规律。

现有针对半开式叶轮离心泵的研究多集中在单相流条件下的不稳定流动特性，关于固液两相流磨损规律的研究多为颗粒参数与叶片磨损速率的外在关联。但是，从动力学机理的内在角度来讲，泄漏涡对流道的阻碍作用会改变颗粒的运动趋势，包括颗粒运移方向和速度，同时颗粒穿过涡会破坏涡结构，因此颗粒撞击、泄漏涡变化和颗粒运动轨迹之间的相互作用加剧了磨损行为的复杂性和多变性。而对于固液两相流条件下半开式叶轮离心泵在不同颗粒体积浓度时泄漏流特性、颗粒运动特性和磨损特性之间内在关系的研究较为匮乏，尤其缺乏颗粒运移对流体扰动的影响。因此，本文采用双向耦合的欧拉-拉格朗日方法，考虑流体-颗粒间的相互作用，同时结合Finnie 磨损模型，通过数值模拟探究不同颗粒相体积浓度对半开式叶轮离心泵内固液两相流场及过流部件磨损规律的影响，深入分析颗粒运移、泄漏涡结构和过流表面磨损之间的交互作用机制，拟为固液两相流半开式叶轮离心泵优化设计和安全稳定运行提供理论参考。

1 数学模型

1.1 液相

本文中的颗粒浓度较小，将半开式叶轮离心泵内液相均视为三维不可压缩流体，连续性方程和动量方程分别如式（1）和式（2）所示，动量交换源项为式（3）[20]：

式中u为流体速度，m/s；p为静压，Pa；ρ为流体密度，kg/m3；μ为流体的动力黏度，N·s/m2；考虑固液两相的交互作用，通过增加一个固液两相动量交换的源项Fi（i=1,2,3）表示颗粒对流体的影响，FD为曳力，N；FB为浮力，N；FM为虚拟质量力，N；FP为压力梯度力，N；Vcell是一个计算单元体积。

1.2 固相

固体离散相模型粒子轨迹的计算是独立的，单个粒子在特定时间间隔内被追踪运动轨迹[21]。半开式叶轮离心泵中颗粒运动轨迹的改变受重力、曳力、虚拟质量力、Basset 力、Saffman 升力和Magnus 升力等主导，由于连续相为水相时Basset 力、Saffman 升力和Magnus 升力相对于曳力非常小，且Saffman 升力和Magnus 升力仅对直径处于1～10 μm 的颗粒有明显影响[22-23]。本文的颗粒粒径为0.5 mm，且连续相为水相，因此仅对曳力、重力、浮力、虚拟质量力和压力梯度力进行分析。控制方程为广义牛顿第二定律，可表示为[24-25]

式中mp为粒子质量，kg；up为粒子速度，m/s。

式中CD为曳力系数；Rep为颗粒雷诺数；ρp为颗粒密度，kg/m3；dp为颗粒直径，mm。

重力FG和浮力FB可表示为

虚拟质量力FM可表示为

其中，CM为虚拟质量系数0.5。

压力梯度力FP可表示为

1.3 磨损模型

颗粒对部件过流表面进行撞击和切割，导致部件变形，材料发生疲劳破坏。产生的磨损是与颗粒特性、冲击条件和壁材特性相关的函数。国内外学者常采用的磨损模型有：Finnie 模型，DNV 模型，Oka 模型以及Ahlert 磨损模型。DNV 模型、Oka 模型的模型修正数据均来自气固两相流动，与本文的液固两相流环境不同，其中DNV 模型未考虑不同角度下磨损机制的变化[26]，且Oka 模型参考的基准冲蚀速率为冲击角度90°时的工况，与离心泵常见的倾斜角度冲击机制不同[27]，而Ahlert 模型根据经验和大量试验数据进行拟合得出，并未从磨损过程中材料去除机制出发[26]。Finnie 模型从材料去除的颗粒位移和切削机制出发，并进行不同角度下磨损机制的区分，特别适用于离心泵等水力机械倾斜冲击角度下的磨损机制[28]，更符合本文的研究条件。因此，本文采用Finnie 磨损模型研究固液两相条件下半开式叶轮离心泵过流部件的磨损规律。

Finnie 提出的经典磨损模型如下[29]：

式中E为磨损量无量纲参数；k为获得无量纲冲蚀因子的常数；Vp为固相颗粒撞击速度，m/s；n为速度指数，与壁面材料属性相关，常用金属材料取值范围为2.3～2.5；f(θ)是关于颗粒冲击角的无量纲函数。

其中，θ=18.42°是区分滑动磨损和冲击磨损的临界值，θ＜18.42°，主要为滑动磨损，θ＞18.42°，则冲击磨损占主导地位[30]。

2 计算模型及网格划分

2.1 模型描述

研究对象为一台半开式叶轮离心泵，主要设计参数为：流量Qd=47 m3/h，扬程Hd=7 m，转速n=980 r/min。叶轮主要几何尺寸为：叶片进口安放角β1=16.6°，叶片出口安放角β2=18.6°，包角Φ=99.4°，叶轮进口直径D1=100 mm，叶轮出口直径D2=232 mm。计算域为进口管、叶轮和无叶扩压器（图1a）。

图1 半开式叶轮离心泵计算域和网格Fig.1 Calculation domain and mesh of semi-open centrifugal pump

2.2 网格划分及无关性验证

采用ANSYS ICEM 软件对半开式叶轮离心泵进口管、叶轮和无叶扩压器模型进行六面体结构化网格划分。为消除网格数量对计算结果的影响，采用美国机械工程协会（American Society of Mechanical Engineers，ASME）推荐的网格收敛指数GCI 进行网格离散误差的估计[31-33]，对网格进行无关性验证。该方法需要设置三套不同数目的网格，分别为粗糙网格、中等网格和细密网格。

本文选择叶片扭矩和叶轮出口总压作为关键变量，消除变量之间带来的运算误差。计算设计工况下GCI 网格离散误差的估计方法中的各参数，得到叶片扭矩的近似相对误差（中等-粗糙和细密-中等）分别为2.442%和0.436%；总压的近似相对误差分别为2.175%和0.199%；叶片扭矩的外推相对误差分别为0.512%和0.075%；总压的外推相对误差分别为0.213%和0.015%；叶片扭矩的不确定度分别为0.643%和0.093%；总压的不确定度分别为0.267%和0.019%，3 套网格以渐进形式收敛。综合考虑计算精度和效率，最终确定选取中等网格，各部分网格数为叶轮5 561 412，进口管427 276，无叶扩压器976 080，网格数共6 964 768。半开式叶轮离心泵网格如图1b 所示。

2.3 数学计算方法及边界条件设置

本文基于SSTk-ω两方程湍流模型，采用双向耦合欧拉-拉格朗日方法求解半开式叶轮离心泵内的固液两相流动，将液相视为连续相，固体颗粒视为离散相。叶轮设置为旋转域，进口管和无叶扩压器均设置为固定域，壁面处设置为无滑移壁面；流体介质为水，温度为25 ℃，密度为997.05 kg/m3；进口处给定总压，假定颗粒为球形，颗粒密度为2 650 kg/m3，进口处颗粒和流体速度相等，且颗粒在进口面上均匀分布；出口给定质量流量。

2.4 数值模拟的验证

2.4.1 试验设备及方法

试验测量工作在离心泵闭式试验台上进行，试验系统的详细描述可参考我们的前期工作[34]。转速通过变频器进行调节，流量通过在出口管路上安装的电磁流量计测量，压力通过在进出口管路上布置的压力传感器测量，扭矩通过安装在泵与电机之间的扭矩转速仪测量。试验测量时通过数据采集设备将测量参数（转速、流量、进口压力、出口压力、扭矩）转换为电流信号，经信号线传送至数据采集系统，数据采集系统将其转换为可识别的数字信号，进行数据采集，计算得到离心泵的扬程和效率，对比清水工况下半开式叶轮离心泵的扬程和效率的计算值和试验值，验证数值模拟的可靠性。

2.4.2 外特性验证

为了验证对半开式叶轮离心泵性能模拟的准确性，对清水工况下离心泵的扬程和效率的模拟和试验结果进行比较。如图2 所示，数值模拟结果与试验值分布一致，扬程最大相对误差7.52%，最小相对误差0.96%，平均相对误差3.77%；效率最大相对误差7.78%，最小相对误差5.61%，平均相对误差6.41%。数值模拟与试验结果具有相同的规律，相对误差在可接受范围内。

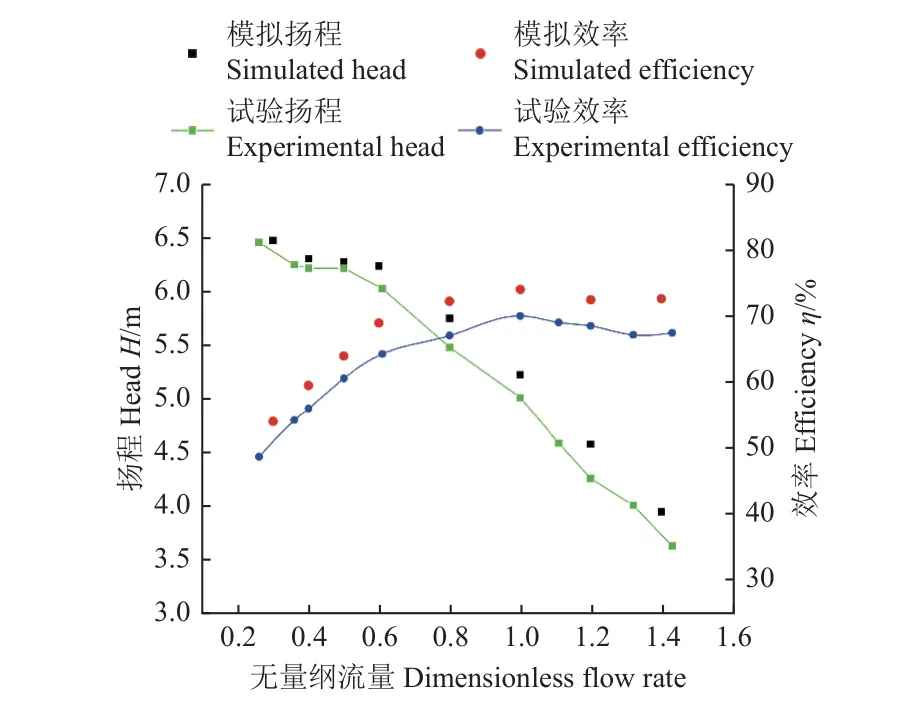
图2 试验与数值模拟外特性结果对比图Fig.2 Comparison of the head and efficiency between experimental and numerical results

2.5 试验设计及方法

根据中国泥沙问题严重的河流沿岸水力机械运行规律，平均固相体积浓度超过2%，最大固相体积浓度超过4%，同时参考了国内外众多学者[9,14,30]在研究不同固相浓度工况下离心泵的内部流场时所选择的固相浓度范围（多为1%～10%）。本文选择在设计转速980 r/min、设计流量1.0Qd、dp=0.5 mm 颗粒粒径的条件下，对比分析4种颗粒相体积浓度（Cv=1%、3%、5%、7%）对半开式叶轮离心泵泄漏涡特征和磨损特性的影响。

为了便于分析半开式叶轮离心泵内的固液两相特性、泄漏涡特性及磨损特性，采用ANSYS 软件对计算结果进行后处理，得到叶轮内部的的压力分布、泄漏涡结构、颗粒轨迹、颗粒平均体积分数分布及磨损分布。

采用Omega 准则捕捉阈值R为0.52 时各颗粒体积浓度下的泄漏涡结构，众多国内外学者证明阈值R为0.52 时具有阈值不敏感特性，并能同时有效识别强、中、弱多种涡结构[35]。为了定量识别涡结构，采用标准螺旋度Hn着色，Hn表示涡矢量与相对速度矢量夹角的余弦值，二者方向相同时Hn为1，正交时为0，相反时为-1[34]。为了能深入理解泄漏涡的运动机理，采用涡量输运方程对叶顶间隙区域的泄漏涡结构进行更详细的分析，涡量输运方程如下[36-38]：

式中 Ω为涡矢量；W为相对速度矢量；ω为旋转角速度，rad/s；ν为流体运动黏度，Pa·s。方程左边表示涡量的变化速率，右边第一项为相对涡量拉伸项（Relative vortex stretching，RVS），由相对速度梯度引起涡的拉伸和弯曲；第二项为涡膨胀项，反映流体可压缩性引起的涡量变化情况；第三项为科氏力项（Coriolis force，CORF），与旋转运动有关；第四项为斜压扭矩项，表示压力梯度与密度梯度对涡量的影响；最后一项黏性扩散项（Viscos diffusion，VISD）主要是由于流体的黏性引起的。对于不可压缩流体，忽略第二项和第四项。由于叶顶间隙的存在，叶轮内部尤其是靠近叶顶区域的不稳定流动复杂，已有工作对叶轮进出口环量进行了分析[2]，发现叶顶间隙对叶轮的影响主要体现在靠近叶顶侧，因此选取0.93 叶高（Span=0.93）（图3）对清水和固液两相工况的流场和涡系特征（RVS、CORF 和VISD）的分布规律进行分析。

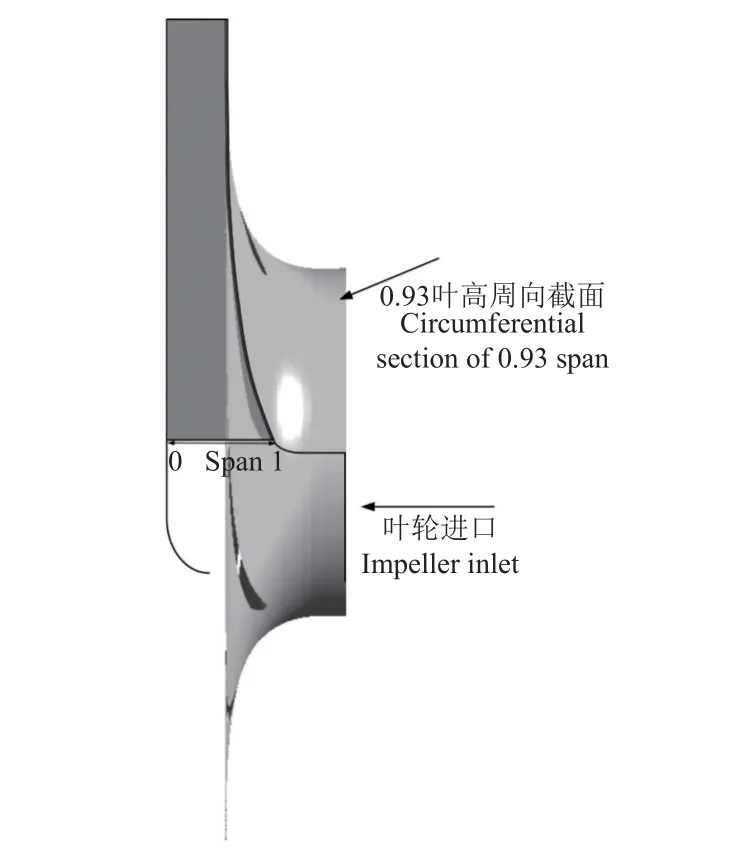
图3 叶高（Span）示意图Fig.3 Diagram of the blade height (Span)

3 结果与讨论

3.1 半开式叶轮离心泵固液两相流动特性

3.1.1 颗粒体积浓度对泵性能的影响

由图4 可知，由于固体颗粒密度远大于液体的密度，加入较小体积浓度的颗粒时，固液混合介质的密度增加，泵的有效功率增加，同时颗粒的存在抑制了边界的流动分离，减少了涡流脱落造成的损失，因此泵的扬程和效率相比于清水工况均增大。随着颗粒体积浓度的增大，颗粒之间相互干扰，发生更多的碰撞和摩擦，流体输送颗粒所需的能耗增加，因此泵的扬程和效率明显下降。

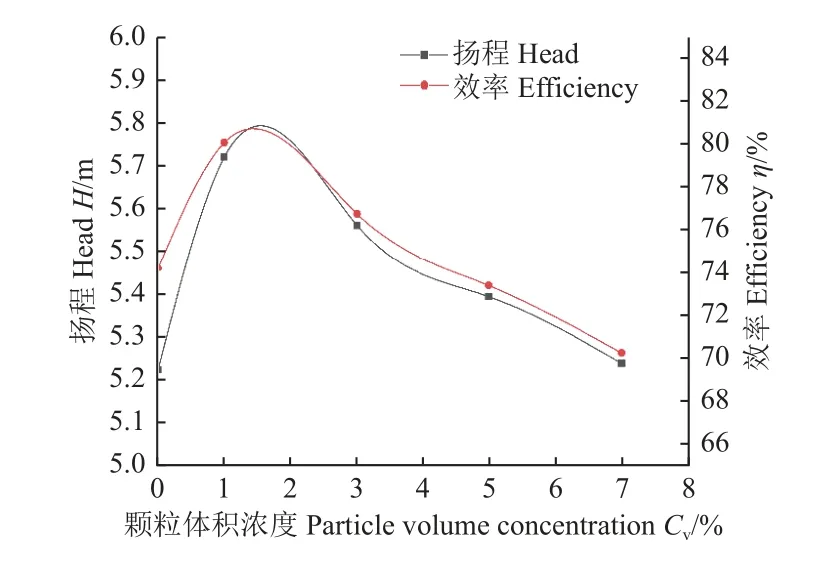
图4 不同颗粒体积浓度外特性变化曲线Fig.4 Head and efficiency curve with different particle volume concentration

3.1.2 叶轮内部流场特性

图5 为设计流量下0.93 叶高截面的压力分布图。由于叶片对吸入介质做功，流场压力沿着叶轮进口向出口方向逐渐增大。清水工况下，由于叶顶间隙的存在，相对液流角的增大造成叶轮进口形成较大的负冲角，结合叶片压力面与吸力面的压差，二者共同驱动形成泄漏流，导致叶片吸力面进水边出现面积较大的低压区。相比于清水工况，颗粒的堆积导致叶轮流道内的压力值普遍升高，最大压力上升4%。部分颗粒在叶轮进口处因流道变化和叶轮旋转的离心力，运动方向由轴向变为径向，与叶片前缘发生碰撞，抑制了边界层的不稳定流动，低压区面积减小，但颗粒碰撞后速度减小，流场内部分压能又转化为驱动颗粒继续运动的动能，产生低压，因此低压区面积仅轻微减小。

图5 不同颗粒体积浓度（Cv）0.93 叶高截面压力分布图Fig.5 Pressure distribution of 0.93 span with different particle volume concentration (Cv)

3.2 颗粒相体积浓度对泄漏涡特性的影响

3.2.1 泄漏涡结构特征

各颗粒体积浓度下的泄漏涡结构如图6 所示。颗粒体积浓度为1%时，少量颗粒的加入对泵内涡流结构的影响较弱，流道中泄漏涡、分离涡和通道涡与清水工况相似。随着颗粒体积浓度的增加，在曳力、离心力和惯性力的耦合作用下，颗粒对流体的撞击频率和跟随流体流入叶顶间隙的颗粒数量增加，流动的不均匀性增强，涡流的破碎程度逐渐加剧，破碎分离的涡流间通过周向运动进行融合。同时，流体旋转消耗的能量增大，抑制了泄漏涡、叶顶分离涡、通道涡的发展，其中二次泄漏涡与主流卷吸形成的二次泄漏流强度明显减弱。

3.2.2 泄漏涡系特征

图7 为叶顶间隙层的相对涡量拉伸项（RVS）分布，随着颗粒相体积浓度的增加，颗粒对叶片前缘的碰撞更加频繁，驱动叶片前缘的流动分离，因此叶片前缘的高RVS 区逐渐增大。颗粒相体积浓度的改变对高RVS 区域在叶片吸力面侧的带状分布趋势影响较小，但颗粒的冲击导致吸力面侧破碎分离出更多的漩涡。

科氏力项（CORF）分布如图8 所示，叶轮的旋转产生科氏力并导致在叶片压力面和吸力面形成压力梯度，泄漏流受到压力梯度的驱动而形成。当颗粒相体积浓度为1%时，固液两相工况下的CORF 分布与清水工况相似，说明较小颗粒浓度对叶轮旋转产生的压力梯度影响作用较小。随着颗粒相体积浓度的增大，叶片前缘受颗粒撞击脱落的涡旋强度增加，叶片吸力面侧的高CORF分布区波动均增大，面积减小，反映出流场不稳定性增强。当颗粒相体积浓度增至7%时，区域A 中吸力面中部的高CORF 区明显波动、分裂，这是由于颗粒的不断累积，在这一区域的流体驱动其偏转跟随运动消耗的能量增多，造成涡量出现一定程度的减少。

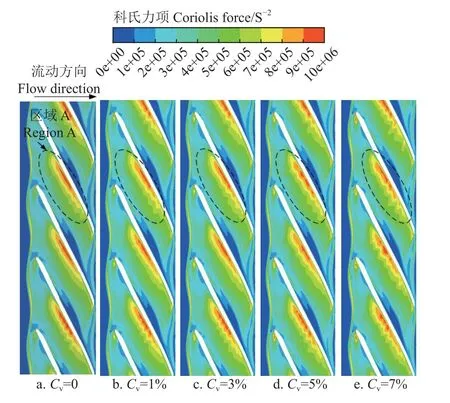
图8 不同颗粒体积浓度科氏力项分布Fig.8 Distribution of Coriolis force item with different particle volume concentration

黏性扩散项（VISD）分布如图9 所示，在叶顶间隙层，叶片压力面与吸力面的压差形成微射流，微射流的运动方向与叶片旋转方向相反，因此与主流和固定的前盖板形成相对运动，导致在壁面处产生涡量。随着颗粒体积浓度的增加，固液两相介质粘性作用的变化及颗粒的运动影响涡流向流体内部的扩散，涡旋难以稳定发展，因此高VISD 区的波动更加明显，同时伴随着剧烈的涡旋分离、融合。

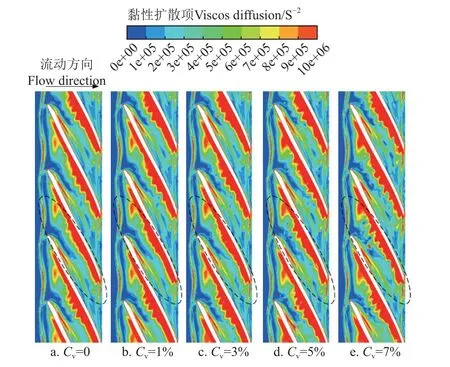
图9 不同颗粒体积浓度黏性扩散项分布Fig.9 Distribution of viscos diffusion item with different particle volume concentration

3.3 颗粒相体积浓度对磨损特性的影响

不同颗粒体积浓度下颗粒速度及轨迹如图10 所示。当Cv＜3%时，仅少量颗粒跟随流体进入叶顶间隙，受到叶顶泄漏涡的阻碍及压力梯度的作用，颗粒穿过叶顶间隙进入吸力面侧后跟随泄漏流运动发生偏转，运动方向由周向变为径向，并与叶片吸力面靠近叶顶处在出水边发生撞击；当Cv＞3%时，随着颗粒体积浓度的增加，流入叶顶间隙的颗粒数量增多，运动至叶片吸力面出水边靠近叶顶处堆积的颗粒增多。

图10 不同颗粒体积浓度下颗粒速度和轨迹Fig.10 Particle velocity and trajectories with different particle volume concentration

同时，颗粒体积浓度越大，颗粒间的排挤导致颗粒逐渐占据整个流道，在叶片吸力面出水边靠近叶根处堆积的颗粒数量增多，且明显多于在叶顶附近聚集的颗粒，说明大部分颗粒在流道中运动时靠近后盖板，叶顶间隙泄漏涡扩散到叶根处时对颗粒的运动已无明显影响。

不同颗粒体积浓度下叶片表面及后盖板的平均颗粒体积分数分布情况如图11 所示。当颗粒体积浓度增大，同等粒径下颗粒数量增多，由于颗粒本身粒径较大，则质量和惯性力较大。

在进入叶轮后颗粒保持原有的轴向运动趋势的能力较强，容易较早的偏转对后盖板进行冲击。同时，压力梯度力和曳力的耦合作用限制了颗粒跟随流线移动，驱使其产生明显的向叶片压力面侧运动的趋势，因此随着颗粒体积浓度增大，聚集在后盖板和叶片压力面侧进水边颗粒明显增多，且分布在后盖板的颗粒多于叶片。

图12 所示，随着颗粒相体积浓度的增大，固相颗粒与过流部件的接触和碰撞几率增加，过流部件的磨损情况逐渐加重。颗粒在流道中运动时，径向的惯性力不能抵消叶轮旋转的离心力，导致后盖板磨损严重区域发生在曲率最大处及叶片曲率最大处的交界处。粒径0.5 mm的颗粒属于粒径较大颗粒，自身质量大，惯性大，流体对颗粒的裹挟能力差，因此叶片压力面侧磨损区域主要集中于进水边至中部。

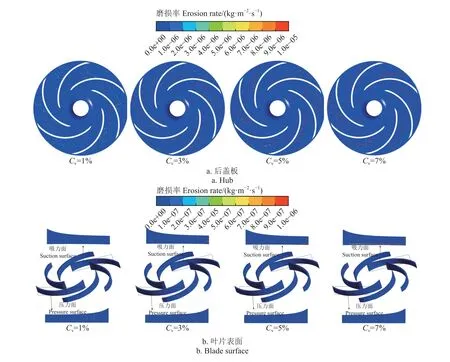
图12 不同颗粒体积浓度下磨损分布Fig.12 Erosion distribution with different particle volume concentration

当Cv＜3%时，受到叶轮旋转的离心力和叶顶间隙泄漏涡的曳力共同作用，颗粒转变为轴向运动进入流道并易在叶片前缘靠近叶根处与壁面发生撞击，诱发严重磨损；同时，颗粒通过叶顶间隙层的流道时受泄漏流的阻碍会迅速转向，绕过低速区偏向叶片吸力面侧运动，导致颗粒易在吸力面侧出水边与叶片发生撞击，撞击角较大，因此吸力面出水边靠近叶顶的区域磨损严重且呈现点状磨损。

当Cv＞3%时，颗粒相体积浓度增大，流入叶顶间隙的颗粒增多，吸力面出水边靠近叶顶的点状磨损加剧；流道内颗粒之间的排挤严重，部分颗粒偏离原有的运行轨迹，跟随流体偏向吸力面侧运动，对吸力面侧进行冲击，撞击角较小，因此吸力面侧出水边靠近后盖板的位置也出现严重磨损，磨损区域呈现线状磨损且向叶片进水边方向延伸。由图13 可知，颗粒相体积浓度的增大，叶片表面及后盖板磨损率均逐渐增大，但后盖板磨损率增速更快，当颗粒相体积浓度大于3%时，后盖板平均磨损率超过叶片平均磨损率。