一种基于幅度补偿的毫米波近场成像算法*

杨翠翠,宋家平,卓智海

(1.北京信息科技大学 信息与通信工程学院,北京 100101;2.中国船舶工业系统工程研究院,北京 100036)

0 引 言

毫米波具有较强的穿透能力,能获得目标的位置、尺寸和形状信息,实现高分辨率成像,在安全检测[1-2]、医疗诊断[3]及无损检测[4]等领域获得了广泛应用。

毫米波成像通常分为主动式和被动式两种:主动式通过接收发射信号回波,采用相关成像算法进行处理获得目标图像[5];被动式主要通过检测物体辐射的能量得到。因主动成像方式受环境影响较小而具有较大优势,常见算法包括反向投影算法和全息成像[6]等。全息成像主要利用中频信号的振幅和相位信息进行目标重建[7],因拥有较高成像质量获得众多学者的青睐。文献[8]提出了一种基于匹配滤波的重建方法,采用卷积操作,未引入平面波叠加的近似计算,但其忽视了幅度因子对成像质量的影响。文献[9]将全息成像应用到稀疏多站雷达成像系统中,在信号模型中加入幅度因子,考虑了路径传播损耗对成像质量的影响,但存在平面波叠加的近似问题。文献[10]提出了一种三维距离徙动算法,推导了信号频谱的精确表达式,未引入近似计算,但采用的插值操作影响了成像效率。

针对上述文献研究存在的问题,本文提出了一种基于幅度补偿的毫米波近场成像算法。该算法保留了幅度因子,在考虑幅度补偿对图像产生影响的同时采用卷积运算、空间傅里叶变换及降维等操进行目标重构,其中降维操作的引入能够降低算法处理复杂度。实验验证与图像质量评估指标客观分析表明,相较于全息成像,本文所提方法不仅可以改善图像重构质量,还能加快成像处理速度。

1 全息图像重建

本文采用二维合成孔径雷达成像系统来获取水平和垂直方向的高分辨率,系统中雷达通过滑轨的移动在水平和垂直方向上均匀采样,雷达会在每一采样点向目标发射毫米波信号,并采集被测目标的散射回波[11]。当完成预定平面的扫描后,对回波信号进行处理,即可获取与长阵列等效的空间分辨效果[12]。

距离天线的区域可分为近场和远场两种,两区域的分界线可取半径R=2L2/λ,L是阵列的最大孔径,λ是波长。当R<2L2/λ时,信号在近场场景下传播,接收信号为球面波模型;当R>2L2/λ时,为远场场景,接收信号为平面波模型。本文将在近场场景下开展雷达成像算法的研究。

建立雷达运动模型如图1所示,定义坐标系的xoy平面为雷达扫描平面,任意扫描点坐标为(x,y,0)。目标平面上的任意散射点为(x′,y′,z′),Δx和Δy分别为水平和垂直方向上的空间采样间隔。定义z轴方向为雷达扫描平面的深度方向。

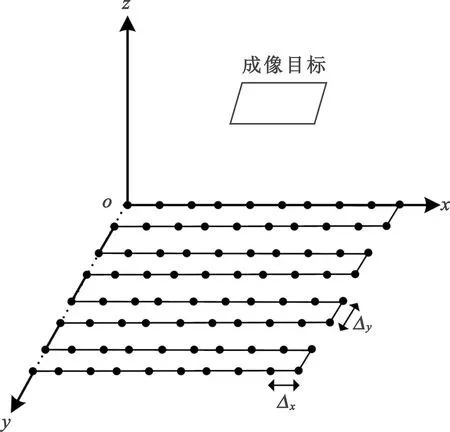
图1 成像系统模型示意

本文采用调频连续波作为发射信号模型,成像算法的主要目的是从雷达回波中恢复出目标的散射系数。回波数据s(x,y,k)可以认为是被测目标上各个散射点与该点往返相位的叠加,即

(1)

式中:目标散射系数为p(x′,y′);波数k=2πf/c,f为频率,c为光速。雷达扫描点与目标散射点的距离为

(2)

基于球面波展开的全息成像通常忽略幅度因子R-2[1],故接收到的信号可近似为

s(x,y,k)=∬p(x′,y′)ej2kRdx′dy′ 。

(3)

式(3)中指数项表示球面波。基于球面波可以分解成平面波叠加的思想[1],采用驻定相位定理将指数项进行近似计算,得

ej2kR≈∬ej(kx(x-x′)+ky(y-y′)+kzz′)dkxdky,

(4)

(5)

式中:kx,ky和kz分别为波数域的3个分量。将式(4)代入式(3)得

s(x,y,k)=∬∬p(x′,y′)×

ej(kx(x-x′)+ky(y-y′)+kzz′)dkxdkydx′dy′。

(6)

重排积分顺序,得

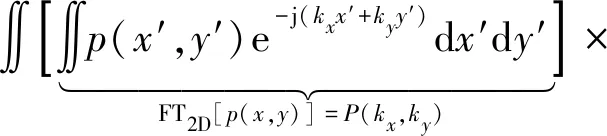
ejkzz′ej(kxx+kyy)dkxdky。

(7)

式中:p(x′,y′)的二维空间傅里叶变换为P(kx,ky)。所以重建图像的波数域形式为

s(x,y,k)=IFT2D[P(kx,ky)ejkzz′],

(8)

P(kx,ky)=S(kx,ky,k)e-jkzz′。

(9)

式中:s(x,y,k)的二维空间傅里叶变换为S(kx,ky,k)。对式(9)进行傅里叶逆变换,可得多个波数下的目标图像,最后在多个波数下进行相干叠加,重建目标图像为

(10)

因此,传统二维近场全息成像的处理过程描述如下:

1)对雷达获取的回波信号s(x,y,k)在水平和垂直方向上进行二维空间傅里叶变换,将其变换至波数域S(kx,ky,k);

2)将参考函数e-jkzz′与宽带回波信号的波数谱相乘,对整个成像区域回波数据的相位进行校正;

3)进行二维傅里叶逆变换,将波数域转换至空间域,得到不同波数下的目标散射系数;

4)将不同波数下的目标图像进行相干叠加,得到位于参考平面上完全聚焦的目标散射强度分布图。

2 基于幅度补偿的近场成像算法

二维全息成像忽略幅度因子影响成像质量且成像效率较低。针对以上问题,本文提出一种基于幅度补偿的近场成像算法。该算法采用幅度补偿和降维操作,以提高成像质量与效率。

将式(1)的回波信号模型展开,得

s(x,y,k)=∬p(x′,y′)×

(11)

不同于全息成像采用驻定相位定理进行球面波的近似计算,本文所提算法采用卷积运算,通过保留幅度因子,将式(11)改写成式(12)的形式:

(12)

式中:“*”表示进行二维卷积运算。

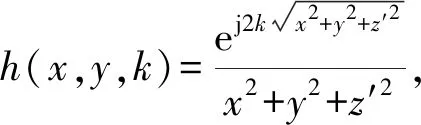
s(x,y,k)=p(x,y)*h(x,y,k) 。

(13)

将式(13)进行傅里叶变换可得

S(kx,ky,k)=P(kx,ky)·H(kx,ky,k) ,

(14)

H(kx,ky,k)=FT2D(h(x,y,k))=

exp(-j(kxx+kyy))dkxdky。

(15)

在近场场景与有限雷达孔径的约束下,对式(14)进行变换,得

P(kx,ky)=S(kx,ky,k)/H(kx,ky,k) 。

(16)

对式(16)进行二维傅里叶逆变换,可得到多个波数下的目标图像,最后在多个波数下进行相干叠加,重建目标图像为

(17)

式(17)中的积分只与k有关,傅里叶逆变换只与kx和ky有关[13]。为减少计算量,提高算法重构速度,可以交换积分运算和傅里叶逆变换的次序,先进行积分运算再进行傅里叶逆变换。通过这种降维操作,将原本进行傅里叶逆变换的三维数据降为二维进行处理。故将式(17)进行优化后可得

(18)

因此,基于幅度补偿的近场成像算法处理过程描述如下:

1)对雷达获取的回波信号s(x,y,k)及考虑幅度因子的参考函数h(x,y,k)分别在水平和垂直方向上进行二维空间傅里叶变换,将其从空间域变换至波数域,得到S(kx,ky,k)和H(kx,ky,k);

2)对S(kx,ky,k)和H(kx,ky,k)进行相除运算,采用降维操作在多个波数下相干叠加,得到聚焦图像的波数域形式;

3)执行二维傅里叶逆变换,得到最终的目标散射强度分布图。

由以上分析可知,该算法主要包括卷积运算、幅度补偿、傅里叶变换和降维操作等步骤,其中将回波信号进行卷积运算是经典匹配滤波方法[8]的重要环节。本文基于该方法,首先进行幅度补偿,考虑了幅度因子对成像质量的影响,其次加入降维操作提高成像效率。

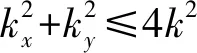
当目标与雷达孔径之间的距离满足R>2L2/λ或R≫L时,天线阵元到成像目标之间的距离近似为目标平面与雷达扫描平面之间的距离,算法中与参考函数相关的项对信号的校正效果减小[8]。所以可以根据不同的成像场景,选择合适的成像算法。

3 实测数据验证

本文搭建了一套二维合成孔径雷达成像系统,通过实测数据来对算法的有效性进行验证。整个成像系统主要由毫米波雷达板、两轴机械扫描滑轨和成像处理软件组成。其中,毫米波雷达板采用TI公司的IWR1443BOOST和DCA1000评估板,主要用于完成雷达信号的发射与接收,并将接收到的回波数据与计算机设备进行实时通信,如图2所示;两轴机械扫描滑轨提供雷达采样的移动平台,如图3所示;成像处理软件采用Matlab完成,主要用于回波信号的图像重建。

图2 毫米波雷达板

图3 两轴机械扫描滑轨及其控制模块

成像目标为一把剪刀,实物如图4所示,选取距离雷达310 mm的目标平面进行成像。在这种参数设置下,要获得约3 mm的成像分辨率,水平和垂直方向的扫描孔径大小约200 mm。为满足空间采样准则,产生无鬼影图像,空间采样间隔需小于半波长,故在水平方向和垂直方向上将空间采样间隔分别设为1.6 mm和2 mm。因成像系统采用单个发射与单个接收天线,收发天线相距很近,故可以近似为单站雷达成像系统。实验采用的参数与运动场景参数设置如表1所示。

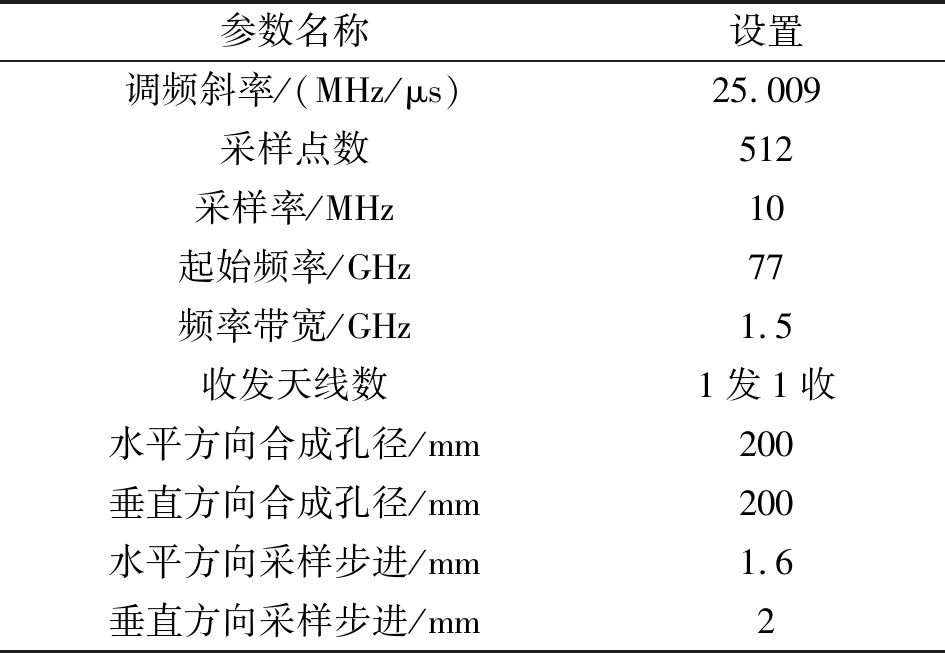
表1 参数设置

图4 剪刀实物

首先对单一目标平面进行成像质量与效率的分析。由图5和图6可以看出,在成像距离平面确定的情况下,全息成像和本文所提算法都可以较好地重构出剪刀的轮廓,而对于一些目标细节,本文所提算法的重构精度更高,具体表现在红色标注的部分。此外,采用图像熵进行客观评估,当f(i,j)表示重建后的图像像素时,图像熵的计算方法如式(19)所示,熵值越小,图像的聚焦质量越好[15]。因此,对于全息成像和本文所提算法的成像结果,其图像熵值也是合理的,本文所提算法的熵值为3.858 2,小于全息成像的熵值3.863 2,故本文所提算法聚焦质量更好,图像重构质量得到提高。在图像重构效率上,全息成像、经典匹配滤波方法、经幅度补偿的匹配滤波方法和本文所提算法图像重构时间分别为9.700 8 s,5.198 8 s,5.441 3 s和4.360 7 s,如表2所示。相对于经典匹配滤波方法,本文所提算法虽因进行幅度补偿而增加了时间消耗,但其经降维处理后花费更少的成像时间。故对于单一目标成像平面,本文所提算法不仅能够提高成像质量,而且还能减少成像处理时间。

表2 单目标成像处理所用时间对比

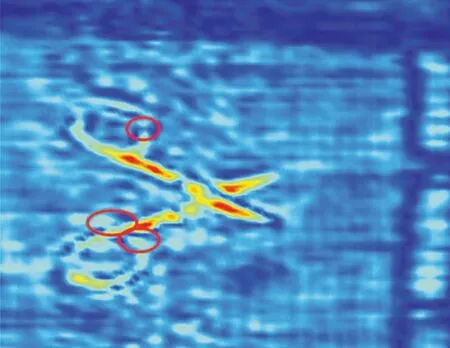
图5 全息成像结果

图6 本文所提算法成像结果

(19)

对于实际近场成像场景,为保证成像效果,通常预先测量成像距离。但对于立体目标或多目标来说,单一成像距离的确定难以保证囊括所有目标散射点。而通过多距离遍历,采用最大值投影的方式可以得到更多目标信息[16]。此次采用3DRIED[17]中的数据进行算法验证,目标实物图如图7所示,两个目标分别放在距离雷达扫描平面约60 cm和70 cm的位置。图8～10分别为相同成像距离范围内全息成像、经典匹配滤波方法及本文所提算法的最大值投影成像结果。对比图9与图10,两者以是否进行幅度补偿为变量,可以看出,图10中左侧较近目标的图像重构质量更好,这说明幅度因子会影响成像效果,进行幅度补偿能提高图像重构质量。对比图8与图10,两者分别为全息成像与本文所提算法的成像结果,在右侧目标红色标记处,图10的杂波较少,可得本文所提算法受杂波旁瓣的影响较小,抗杂波性能更好。在图像客观评价指标上,全息成像和本文所提算法的图像熵分别为3.944 2和3.883 4,故本文所提算法的图像聚焦质量更好。在成像效率上,不同处理过程的成像时间如表3所示,显然本文所提算法消耗时间最少。故对于多目标或非单一成像平面来说,本文所提算法不仅可以提高图像重构质量,还能加快成像处理速度。综合以上两种方案对比分析的结果可知,本文所提算法具有一定的优势。

表3 多目标成像处理所用时间对比

图7 多目标实物

图8 全息成像结果

图9 经典的匹配滤波方法成像结果

图10 本文所提算法成像结果

4 结束语

本文在考虑幅度因子对成像质量产生影响的基础上,提出了一种基于幅度补偿的毫米波近场成像算法。该算法首先保留幅度因子,对雷达回波信号进行幅度补偿,其次采用降维操作降低算法复杂度。通过进行单一平面与多平面成像实验,结果表明,相较于经典全息成像,本文所提算法具有一定的优越性,不仅能够提高图像重构质量,还可以加快成像处理速度。

当前成像系统的采样间隔大多满足采样准则,后期可考虑在欠采样状态下进行成像质量与成像效率的研究。