一道中考试题的解法探究与变式演练

冯文波

⦿河北省唐山市第四十九中学

“一次函数的图象与性质”是人教版八年级(下)第十九章的内容.本章既是函数部分的起始章,又是学生后续学习二次函数和反比例函数的基础,所以十分重要.近年来,一次函数成为各地中考的必考内容之一,题型多样,其中难度较大的是解答题中对一次函数的性质、图象与实际运用的考查.

1 真题再现

(2022年河北省中考数学第25题)如图1,在平面直角坐标系中,已知线段AB的端点为A(-8,19),B(6,5).

图1

(1)求AB所在直线的解析式.

(2)某同学设计了一个动画:在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,得到射线CD,其中C(c,0).当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.

①若有光点P弹出,试推算m,n应满足的数量关系;

②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.

2 解法探究

上述真题思路分析及解析如下.

思路分析：第(1)问运用待定系数法.设直线AB的解析式为y=kx+b(k≠0),把点A,B坐标代入求出k,b的值即可.第(2)问的第①小问,由题意知点C(2,0),把点C(2,0)代入y=mx+n,即可求解;对于第②问,由①得n=-2m,则y=(x-2)m,根据题意找到线段AB上的整点,再逐一代入,即可求解.

故AB所在直线的解析式为y=-x+11.

(2)①若有光点P弹出,则c=2,即点C(2,0).

把点C(2,0)代入y=mx+n(m≠0,y≥0),得2m+n=0.故有光点P弹出时,m,n满足n=-2m.

②由①得n=-2m,代入y=mx+n,得y=(x-2)m.

由(1)知AB所在直线的解析式为y=-x+11,所以,线段AB上的其他整点为(-7,18),(-6,17),(-5,16),(-4,15),(-3,14),(-2,13),(-1,12),(0,11),(1,10),(2,9),(3,8),(4,7),(5,6).

因为有光点P弹出,并击中线段AB上的整点,所以直线CD过整数点.

当击中线段AB上的整点(-7,18)时,18=(-7-2)m,即m=-2;

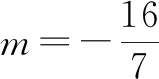
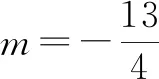
当击中线段AB上的整点(-1,12)时,12=(-1-2)m,即m=-4;

当击中线段AB上的整点(1,10)时,10=(1-2)m,即m=-10;

当击中线段AB上的整点(2,9)时,9=(2-2)m,不存在;

当击中线段AB上的整点(3,8)时,8=(3-2)m,即m=8;

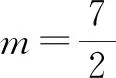
当击中线段AB上的整点(5,6)时,6=(5-2)m,即m=2;

综上所述,满足题意的整数m的个数为5.

总结反思：解答本题的关键是准确理解有光点P弹出,并击中线段AB上的整点,即直线CD过整数点.

3 变式演练

3.1 一次函数与反比例函数的综合题

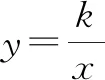
图2

(1)求这两个函数的表达式;

(2)试求上述两个函数图象的另一个交点B的坐标,并借助图象求出使反比例函数的值大于一次函数的值的x的取值范围.

思路分析：(1)将点A的坐标分别代入两个函数的表达式,即可求出b.(2)将两函数解析式联立,求方程组的解,再数形结合即可求解.

由一次函数y=x+b的图象经过点A(1,2),得2=1+b,即b=1.

由(x+2)(x-1)=0,解得x=-2或x=1.

因为点B在第三象限,所以其坐标为(-2,-1).

由图象可知,当反比例函数的值大于一次函数的值时,x的取值范围是x<-2,或0

总结反思：充分利用两函数图象的交点坐标是解决反比例函数与一次函数综合题的关键;在解答第(2)问时,要注意观察图象,同时不能忽视本问的解存在着两种情况.

3.2 与一次函数的图象有密切联系的题型

例2已知点A(6,0),点P(x,y)在第一象限,且x+y=8,设△OPA的面积为S.

(1)求S关于x的函数表达式;

(2)求x的取值范围;

(3)求S=12时,点P的坐标;

(4)画出函数S的图象.

思路分析：通过作垂线,即可求出S关于x的函数表达式;由点P在第一象限,可求出x的取值范围;再由S=12,可确定点P的坐标;最后,根据两个端点的坐标便可画出函数的图象.

(2)由x+y=8与点(x,y)在第一象限,可知x的取值范围为0

(3)当S=12时,x=4,y=4,所以点P的坐标为(4,4).

(4)函数S的图象为一条不包括两端点的线段MN,其中端点分别为M(0,24),N(8,0),如图3.

图3

总结反思：解函数图象信息题的关键在于看懂图象和熟悉实际情境中的数量关系,应用数形结合的思想方法来综合分析、推理.

4 结语

一次函数的性质与图象的综合类问题,具有“覆盖知识面广、涉及知识点多、思路开阔、解法灵活、便于设题”等特点,尤其适合对学生综合能力的全面考查,近年来已成为各地中考的压轴题型之一.因此,要想在数学中考中取得优异成绩,就需要研究压轴题的类型与解题方法[1],特别是在平时备考过程中,要多做中考真题,加强类题演练和变式演练,及时总结反思.“备”是为了“考”,有“备”才能无患.