相干控制的布洛赫表面波偏振转换*
2023-11-24韦进志王金浩陈俊学
韦进志 王金浩 陈俊学
(桂林理工大学理学院,桂林 541004)
光子结构在多光束的相干激发下,通过调控光束间的干涉效应可以对结构的光学响应进行实时的控制.本文研究了介质多层膜结构中相干控制的布洛赫表面波的偏振转换过程.通过在介质多层膜的顶层引入凹槽结构,可以促使布洛赫表面波进行偏振转换.当两束相干的布洛赫表面波分别从结构的左右两端入射到凹槽结构上时,通过设计结构偏振转换系数的相位差和入射相干光束间的相位延迟,不仅可以对布洛赫表面波的偏振转换效率进行动态调控,还可以对结构偏振转换的输出端口进行选择,从而可以实现可控端口传输的表面波偏振转换器件.本文通过改变凹槽的间距,实现了对结构偏振转换系数相位差的设计,通过严格的电磁场仿真验证了本文所设计结构中布洛赫表面波偏振转换的相干控制.本文结果丰富了布洛赫表面波相关器件的研究,在片上集成的光子回路中有着潜在的应用.
1 引言
偏振是光的基本属性之一,通过对光的偏振态进行操控,可以实现许多新颖的光学现象和新的应用[1,2].目前对光的偏振态进行调控是一个研究热点,研究人员通过在电磁超表面结构中引入电控材料(如可变电容、石墨烯等),可以通过外部偏压对自由空间入射光的偏振状态进行动态调控[3-5].另外近年来电磁结构中相干控制的能量转换引起了人们的广泛关注,典型的应用是相干完美吸收(coherent perfect absorber,CPA)[6].通过光场的干涉和耗散的相互作用,可以实现对电磁超表面结构[7-9]、石墨烯结构[10,11]的光吸收进行实时调控.除了吸收损耗外,研究人员还将CPA 效应推广到其他能量的转换形式,从而实现一种不需要非线性效应的全光控制方法,如偏振转换[12,13]、角动量转换[14]、衍射[15]、荧光辐射[16]等.
布洛赫表面波(Bloch surface waves,BSW)是一种存在于电介质多层膜和半无限大均匀介质界面的电磁表面波.BSW 主要利用多层膜中的光子禁带和均匀介质中的全内反射来实现表面波的传输[17].通过调节多层膜结构和均匀介质层可对BSW 的色散和传输特性进行调控.与存在于金属表面的表面等离激元(surface plasmon polaritons,SPPs)类似,BSW 具有对外界环境变化敏感、光学近场增强等特性.BSW 已用于实现高灵敏度的折射率传感[18,19]、增强荧光辐射[20]、增强光吸收[21,22]等领域.与SPPs 不同,由于结构不存在欧姆吸收,BSW 具有低的传输损耗,而且具有横电(transverse electric,TE)和横磁(transverse magnetic,TM)两种偏振模式.鉴于BSW 的优异特性,有望实现基于BSW 的集成光子回路.为了实现这一目标,研究人员在BSW 的波导[23-25]、波前控制[26]、方向性激发[27,28]、共振结构[29-31]、偏振转换[32,33]等方面进行了大量的研究工作.
在文献 [32,33]中,通过在电介质多层膜的顶层引入凹槽结构,可以促使TE 和TM 偏振的BSW进行相互转换,实现相应的功能器件.BSW 的偏振转换效率依赖于结构的几何参数和入射角度,当结构参数和入射角度确定后,BSW 的偏振转换效率一般不能进行改变,这限制了BSW 相关功能器件的开发.本文研究了相干控制的BSW 偏振转换过程.通过在凹槽结构的左右两端分别引入两束相干的TE-BSW,利用两束相干光相位延迟导致的干涉效应,不仅可以对BSW 的偏振转换效率进行调控,还可以对偏振转换的输出端口进行选择,从而可以实现可控端口传输的偏振转换器件.
2 理论模型
本文研究的电介质多层结构由交替的SiO2和Si3N4层组成,总层数为20 层.结构每一层的厚度见图1(a),其中结构顶部SiO2层的厚度为370 nm,其余9 层SiO2层的厚度为126 nm,介质Si3N4层的厚度都为80 nm,整个电介质多层结构被放置在玻璃基底上.根据周期性介质中的电磁理论[17],BSW 的电磁能量在多层膜介质中表现为沿界面指数衰减,其衰减深度由布洛赫波数决定.在结构中,由于TM-BSW 在多层膜中的衰减深度大于TE-BSW,多层膜的层数由TM-BSW 在多层膜的衰减深度决定.经过计算,当多层膜的层数大于20 层时,结构可以有效维持TM-BSW 和TE-BSW的传播.在结构中,顶层SiO2层中刻蚀有3 个相同几何尺寸的矩形凹槽.凹槽的宽度为wg,深度为hg,近邻凹槽间的间距表示为L.其中电介质SiO2,Si3N4和玻璃基底的折射率分别为1.48,2.65 和1.515.在这些结构参数下,电介质多层结构支持TE 和TM 偏振的BSW(表示为TE-BSW 和TMBSW).由于结构由有限层数的多层膜构成,在多层膜的z轴方向会有泄漏模式的能量辐射到基底中,需要用吸收边界层来吸收泄漏模式的辐射能量,从而可以用转移矩阵方法来计算结构中泄漏模式(包括布洛赫表面波)的传播常数[34].模拟中吸收边界层的厚度为1 μm.在波长633 nm 处,通过转移矩阵方法可以得到[35],TE-BSW 和TM-BSW的横向波数β (β=2π/(λ·neff),λ 为真空波长,neff是BSW 的有效折射率)分别为13.08 rad/μm 和10.79 rad/μm.

图1 (a)多层结构的示意图;(b) 结构对应的输入和输出端口示意图Fig.1.(a) Schematic diagram of the considered dielectric multilayer;(b) the schematic diagram of input and output ports in the structure.
当TE-BSW 以角度θi入射到凹槽结构表面时,由于凹槽内外模式有效折射率的变化,将引起入射BSW 的部分反射和透射.除此之外,TMBSW 也能被激发,从而形成BSW 的偏振转换.由于TE-BSW 和TM-BSW 传播常数的差异,激发的TM-BSW 具有与TE-BSW 不同的传播方向.利用导波横向动量匹配的关系,被激发的TMBSW 的出射角度表示为
其中,neff,TE和neff,TM分别是TE-BSW 和TMBSW 的模式有效折射率.由于BSW 的导波特性,模式的反射、透射和偏振转换系数可通过非周期的严格耦合波分析方法(aperiodic rigorous coupled wave analysis,ARCWA)求 得.在ARCWA 中,结构沿z轴方向周期性排列,在相邻周期处通过引入完美吸收边界(perfectly matched layer,PML)来抑制相邻周期的作用,这样ARCWA 能方便处理导波的衍射问题[36,37].在模拟中,为了保证结果的收敛性,ARCWA 中傅里叶展开阶数为160,PML层的厚度为1 μm.
这里忽略结构散射到空气和基底的能量损耗.如图1(b) 所示,对于TE-BSW 和TM-BSW 来说,结构具有4 个输入和输出端口.BSW 入射到结构凹槽上的传播过程可以通过如下的散射矩阵描述:
为了实现BSW 偏振转换的相干控制,两束相干的TE-BSW 分别从结构的左右两端以相同的角度入射到凹槽上.假定从凹槽左右两端入射TEBSW 的复振幅分别表示为=1,=αejψ,其中,α为从右端入射TE-BSW 的相对振幅,ψ 为两束相干光的相对相位延迟.那么在两束TEBSW 的照射下,由于偏振转换作用,在凹槽结构左右两端输出的TM-BSW 强度可以表示为
其中,θr,sp和θt,sp分别对应于偏振转换系数rsp和tsp的相位.这里定义一个方向性偏振转换量M:
从(4)—(6)式中,可以看出结构的方向性偏振转换量M除了与偏振转换系数的振幅有关外,还与入射光的相对相位延迟ψ 和偏振转换系数的相位差θr,sp-θt,sp相关,这些量都可以通过ARCWA 模拟得到.
3 分析与讨论
在研究相干控制的BSW 偏振转换之前,首先分析单束光照射到单个凹槽上的情况.当一束TEBSW 入射到单个凹槽上时,图2 给出了偏振转换系数rsp的幅度随TE-BSW 的入射角度和凹槽宽度的变化.由于TE-BSW 的模式有效折射率大于TM-BSW (neff,TE>neff,TM),当入射角大于55.5°时,偏振转换产生的TM-BSW 表现为倏逝波的形式,不再传播能量.从图2 可以看出,当TE-BSW的入射角在45°—55°范围变化时,结构具有较大的偏振转换系数.在综合考虑偏振转换系数的大小以及TM-BSW 的出射角度,选择TE-BSW 的入射角度 θi=49°,凹槽的宽度为wg=250 nm.

图2 单束TE-BSW 入射到单个凹槽上的情况,偏振转换系数rsp 的幅度随TE-BSW 的入射角度和凹槽宽度的变化Fig.2.Amplitude of polarization transformation coefficient rsp as a function of the incidence angle of TE-BSW and the width of groove.Here,a single TE-BSW beam is incident on a single groove.
分两种情况来讨论结构中相干控制TE-BSW方向性偏振转换的实现过程.首先,当相位差θr,sp-θt,sp=2mπ +π/2(m为整数)时,方向性偏振转换量M表示为
当α=1 时,左右两端入射的TE-BSW 具有相同幅度,M可进一步表示为
式中M正比于 sinψ.在这种情况下,可以通过控制相干光的相位延迟ψ,使得偏振转换产生的TMBSW 在凹槽的左端(M> 0)或右端(M< 0)产生,而结构另外一端的偏振转换被抑制.
在结 构中,BSW 的偏振转换系 数(rsp和tsp)和相应的相位差(θr,sp-θt,sp)主要由凹槽的结构参数决定.图3(a),(b)分别给出了偏振转换系数rsp和tsp的幅度和相位差(θr,sp-θt,sp)随凹槽间距L的变化.凹槽的间距变化主要影响TE-BSW 和TM-BSW 间的干涉效应,从图3 可以看出,当间距L在360—560 nm 范围变化时,结构具有较大的偏振转换系数和相位差变化范围.还可以看出,当间距L=530 nm 时,相位差θr,sp-θt,sp=π/2,符合设计要求.

图3 (a) 偏振转换系数 rsp和tsp 的幅度随凹槽间距L 的变化;(b)偏振转换系数的相位差 θr,sp-θt,sp 随凹槽间距L 的变化.凹槽的宽度和深度都为250 nm,TE-BSW 的入射角度θi=49°Fig.3.(a) Amplitude of polarization transformation coefficients rsp and tsp versus the separation distance L;(b) the phase difference of polarization transformation coefficients θr,sp-θt,sp versus the separation distance L.The width and depth of grooves are 250 nm,the incidence angle of TE-BSW is 49°.
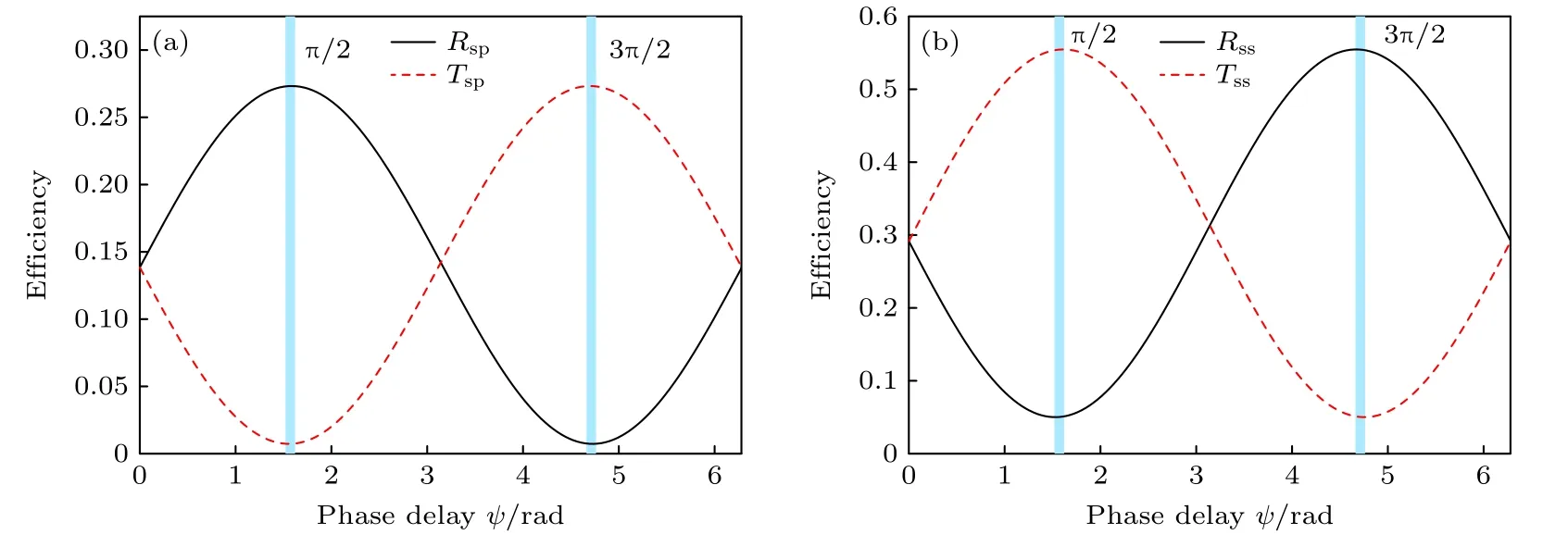
图4 (a)偏振转换强度(Rsp和Tsp)随入射TE-BSW 的延迟相位ψ 的变化;(b)反射率(Rss)和透射率(Tss)随入射TE-BSW 的延迟相位ψ 的变化.其中,凹槽的间距L=530 nm,入射角度 θi=49°Fig.4.(a) Polarization transformation intensities Rsp and Tsp versus the phase delay ψ of incident TE-BSWs;(b) the reflectance Rss and transmittance Tss of TE-BSW versus the phase delay ψ of incident TE-BSWs.The separation distance L=530 nm,the incidence angle θi=49°.
为了能更清晰了解结构中BSW 偏振转换的相干控制过程,采用两束高斯形状的TE-BSWs 光束以入射角49°分别从左右两端照射凹槽结构上,并观察结构的近场分布.高斯光束的半高全宽为10 μm,结构的场量在顶层SiO2界面的上方10 nm的位置采集(z=10 nm).高斯形状的导波通过傅里叶变换成平面波角谱,每个角谱分量通过ARCWA计算出相应的场量,最后叠加相应的角谱分量得到结构在高斯光束相干作用下的电场分布.图5(a)和图5(b)分别展示了在入射光相位延迟ψ=π/2和ψ=3π/2 时,结构在xy平面上的电场振幅分布.当相位延迟ψ=π/2 时,在两束TE-BSWs 的相干作用下,结构偏振转换产生的TM-BSW 主要集中在凹槽的左边端口,而凹槽的右边端口的TM-BSW 被抑制.当相位延迟变为 3π/2 时,凹槽左边端口的TM-BSW 被抑制,右边端口的TMBSW 得到增强,这与(8)式预言的结果一致.

图5 当相位延迟(a) ψ=π/2和(b) ψ=3π/2 时,结构的电场振幅分布.其中凹槽的间距L=530 nm,入射角度θi=49°,白色的点线表示凹槽所在的区域Fig.5.Electric field amplitude distribution of structure for different phase delay (a) ψ=π/2 and (b) ψ=3π/2.The separation distance L=530 nm and the incidence angle θi=49°,the dot lines denote the zone of grooves.
接下来讨论第2 种情况,当相位差θr,sp-θt,sp=2mπ +π(m为整数)时,方向性偏振转换量M表示为
当α=1 时,M=0.在这种情况下,在结构的左端和右端都能产生相同效率的偏振转换,总的偏振转换效率正比于 (|rsp|+|tsp|)2.从图3(b)可以看出,当L=453 nm 时,θr,sp-θt,sp=π,满足设计要求.
在两束TE-BSW 的相干作用下,图6(a)给出了结构偏振转换强度Rsp和Tsp随入射TE-BSW的延迟相位ψ 的变化.TE-BSW 的反射(Rss)和透射 (Tss) 强度随延迟相位ψ 的变化见图6(b).随着延迟相位ψ 的变化,偏振转换强度Rsp和Tsp具有相同的值,这与(9)式描述的结果一致.这种情况下入射的TE-BSW 在凹槽左右两端产生相同效率的偏振转换.当入射的TE-BSW 的延迟相位ψ=π时,TE-BSW 的反射(Rss)和透射(Tss)强度获得极小值,而偏振转换强度获得极大值,这与(4)式和(5)式描述的结果是一致的.另外,从图6(a)可以看出,在相干作用下结构的偏振转换效率可以从12%—34%之间进行动态调控,在相同凹槽数目情况下,这高于单一光束入射的情况(其转换效率约为17%)[32].

图6 (a) 偏振转换强度(Rsp和Tsp)随入射TE-BSW 的延迟相位的变化;(b)反射(Rss)和透射(Tss)强度随入射TE-BSW 的延迟相位的变化关系.其中,凹槽的间距L=453 nm,入射角度θi=49°Fig.6.(a) Polarization transformation intensity Rsp and Tsp versus the phase delay of the incident TE-BSWs;(b) the reflectance Rss and transmittance Tss versus the phase delay.The separation distance L=453 nm and the incidence angle θi=49°.
当两束半高全宽为10 μm 的高斯TE-BSW光束以入射角49°分别从左右两端照射凹槽结构上时,图7 显示了入射光相位延迟ψ=π 时,结构在xy平面内的电场振幅分布.从图7 可以看出,在两束TE-BSW 的相干作用下,经过偏振转换的作用,凹槽的左右两端产生了相同强度的TM-BSW 输出,而入射TE-BSW 的反射和透射被抑制,这样通过相干作用增强了结构的偏振转换效率.

图7 相位延迟 ψ=π 时,结构的电场振幅分布,其中凹槽的间距L=453 nm,入射角度θi=49°,白色的点线表示凹槽所在的区域Fig.7.Electric field amplitude distribution of structure for phase delay ψ=π,the separation distance L=453 nm and the incidence angle θi=49°.The dotted lines dente the zone of grooves.
4 结论
本文研究了介质多层膜结构中相干控制的BSW偏振转换过程.通过在介质多层膜的顶层引入凹槽结构,两束相干的TE-BSW 分别从凹槽结构的左右两端,以相同的角度入射到凹槽结构上.通过设计结构偏振转换系数的相位差以及入射光束间的相位延迟,可以对结构偏振转换效率以及偏振转换的输出端口进行调控.具体来说,当结构偏振转换系数的相位差为 π/2 时,通过调节入射光束间的延迟相位,可以实现结构的偏振转换在凹槽结构的左端或右端产生,相应的另一端口的偏振转换被抑制,实现了方向性的偏振转换;当结构偏振转换系数的相位差为 π 时,凹槽结构左右两端的偏振转换具有相同的效率,结构偏振转换的方向性消失,通过调节入射光束间的延迟相位,可以对结构的偏振转换效率进行控制.本文结果丰富了布洛赫表面波相关器件的研究,在片上集成的光子回路中有着潜在的应用.
