基于偏振动力学的全光储备池计算系统*

方捻 钱若兰 王帅

(上海大学,特种光纤与光接入网重点实验室,特种光纤与先进通信国际合作联合实验室,上海 200444)

在半导体光放大器光纤环形激光器的基础上,提出一种基于偏振动力学的全光储备池计算系统.实验分析了该激光器的偏振动力学状态响应的影响因素,且结合储备池基本属性确定了系统参数的选取范围.通过处理Santa Fe 时间序列预测任务和多波形识别任务来评估该储备池计算系统的网络性能.在合适的系统参数下,仅用30 个虚节点,时间序列预测任务的归一化均方误差可低至0.0058,识别任务的识别率可高达100%.实验结果表明,该偏振动力学储备池计算系统具有良好的预测性能和分类能力,且与已有的基于该环形激光器的强度动力学储备池计算系统的性能相当.该工作为光储备池计算神经网络的研究提供了新的思路.当其偏振动力学和强度动力学一起使用时,该系统有望实现两个任务的并行处理.

1 引言

储备池计算(reservoir computing,RC)是一种简化的递归神经网络新型计算模型[1,2].RC 中储备池的输入权值和内部连接权值都是随机生成且固定不变的,需要训练的只是输出权值[3,4],因此RC 适合于硬件实现.比较节省硬件资源的实现方案是使用单个非线性节点加延迟反馈环的延时型RC.2012 年,Duport等[5]基于半导体光放大器(semiconductor optical amplifier,SOA)实 现全光RC.随后,研究人员使用不同的非线性节点和反馈环结构等方法来提高延时型光子RC 的网络性能.利用半导体激光器(semiconductor laser,SL)的光反馈[6]、光电反馈[7]的RC 实现方案先后被报道.半导体饱和吸收镜[8]、微环谐振器[9]、相干驱动无源光纤腔[10]、半导体环形激光器[11]、圆面六方谐振腔微激光器[12]等作为非线性节点的报道也相继出现.2018 年,本课题组[13]提出基于多反馈环结构提高和控制硬件储备池记忆能力的思想,同年,Hou等[14]提出一种SL 双光反馈RC.2019 年,Chen等[15]提出双光电反馈RC.这些研究成果均利用系统丰富的强度动力学响应来实现储备池计算,属于强度动力学RC 系统.与前述研究不同,2012 年,Martinenghi等[16]报道了基于波长动力学的光电RC 系统的实验结果.2014 年,Nguimdo等[17]证明SL 的相位动力学比其强度动力学能更快地处理信息.

近几年,基于所谓偏振动力学的RC 逐渐成为新的研究热点.Vatin等[18,19]数值研究了利用垂直腔面发射激光器(vertical cavity surface-emitting laser,VCSEL)的偏振动力学增强RC 性能,并进行了实验验证.Guo等[20]利用基于VCSEL 双光反馈的RC 系统,有效地增强了系统的记忆能力.Zhong等[21]构建了基于级联耦合光泵浦自旋VCSELs的深度RC 系统.Jiang等[22]提出利用光电反馈VCSEL 的偏振动力学的RC 结构.Huang等[23]提出并对比研究了自注入和互注入VCSELs 的RC系统.尽管这些VCSEL-RCs 大都声称基于偏振动力学,但实际上利用的只是两个相互垂直的偏振模式的强度动力学,真正基于丰富的偏振动力学响应的RC 还没有看到.

光纤内部存在着双折射效应且随机分布,所以,光纤中传播的光束在不同的部位具有不同的偏振态.对于SOA 光纤环形激光器,光纤环中传输光的偏振态也在不断变化,加上SOA 的非线性效应,该环形激光器可以产生丰富的偏振动力学状态.基于此,王陆唐等[24,25]实验上成功地实现了偏振移位键控光学混沌保密通信;本课题组分析了该环形激光器的输出偏振混沌性[26]及其偏振输出状态[27],并将其成功应用于分布光纤传感[28].

为了进一步拓展SOA 光纤环形激光器的偏振动力学的应用,并为光RC 系统的研究开辟新的方向,本文基于该环形激光器的偏振动力学构建了全光RC 系统,实验分析了系统偏振动力学响应的影响因素,并结合储备池的基本属性确定系统参数的选取范围,最后通过Santa Fe 时间序列预测任务和多波形识别任务与基于该激光器的强度动力学的RC 进行了性能对比.

2 基于SOA 光纤环形激光器的偏振动力学储备池计算系统

2.1 实验系统

基于SOA 光纤环形激光器的偏振动力学储备池计算系统结构如图1 所示,是一个受外调制光注入的SOA 光纤环形激光器.系统使用的非线性节点为SOA,这里采用的是CIP 公司的SOA 模块(SOA-S-C-14-FCA).输入信号经由Tektronix 公司的任意波形发生器AWG(AWG520)产生,再通过Oclaro 公司的2.5 Gbit/s 强度调制器IM(2F014D07)对超辐射发光二极管SLED 产生的宽带连续激光进行强度调制.强度调制光通过光纤耦合器FC1注入储备池中.光纤环形激光器由偏振控制器PC、光隔离器ISO、SOA、延迟光纤和可调光衰减器VOA 组成.其中,PC 采用General Photonics公司的光纤挤压器(PLC-001),用于调整光纤环中光的偏振态.ISO 用来控制光纤环中的光单向传输.延迟光纤为标准单模光纤,其长度决定系统的反馈时延.VOA 为上海瀚宇光纤通信技术有限公司的可调光纤衰减器,用来控制光纤环中光的功率,从而控制系统的反馈光强度.储备池通过光纤耦合器FC2 分出一束光进行输出.这束光经过检偏器和光电探测器PD(OPEAK 公司的InGaAs光电探测器,带宽为150 MHz)转换成电信号.最终使用示波器(PICO 公司的PicoScope 5203 数字示波器)采集电信号,即系统的偏振动力学状态响应,作为储备池内部状态.如果不使用检偏器,直接用PD 探测输出光功率,则得到的是强度动力学状态响应.

图1 基于SOA 光纤环形激光器的偏振动力学储备池计算系统.AWG,任意波形发生器;SLED,超辐射发光二极管;IM,强度调制器;FC,光纤耦合器;PC,偏振控制器;ISO,隔离器;SOA,半导体光放大器;VOA,可调光衰减器;PD,光电探测器Fig.1.Polarization dynamics reservoir computing system based on a SOA fiber ring laser.AWG,arbitrary waveform generator;SLED,superluminescent light emitting diode;IM,intensity modulator;FC,fiber coupler;PC,polarization controller;ISO,isolator;SOA,semiconductor optical amplifier;VOA,variable optical attenuator;PD,photodetector.

延迟光纤长度为1 km.通过计算偏振动力学储备池计算系统输出信号的自相关函数获得系统的反馈时延,即τR=5.088 μs.示波器采样率设置为500 MS/s.

2.2 偏振动力学储备池计算系统模型

偏振动力学储备池计算系统模型如图2 所示.系统包括三个部分: 输入层、储备池和输出层.

图2 偏振动力学储备池计算系统模型Fig.2.Schematic diagram of polarization dynamics reservoir computing system.

在输入层,首先对输入的连续时间信号进行采样得到离散时间序列,在每个采样点保持T时间,其中T为掩码(mask)信号的周期,等于光纤环路的反馈时延τR,然后得到采样保持后的输入信号,再乘以掩码信号和缩放因子γ,得到掩码后的输入信号u(n).掩码信号相当于输入层到储备池的连接权值,一般来说,可以采用二进制掩码、六值掩码、随机掩码或混沌掩码等[29].在本研究中,不同任务根据实际情况选择适宜的掩码信号.预处理后的输入信号经过光强度调制后注入到储备池中.

在储备池层,输入信号以虚节点的形式映射到SOA 光纤环中,SOA 光纤环在输入信号作用下,产生丰富的偏振动力学响应.系统的偏振动力学响应状态可用以下演化方程来描述:

其中N为内部虚节点数;Aij表示虚节点状态xi和xj之间的互连权值;mi表示输入掩码信号的第i个值;β和α分别为输入增益和反馈增益,用于调节注入储备池内的信号强度和储备池内反馈信号的强度,以找到最佳的工作点参数;FNL为非线性函数.研究发现,半导体光放大器具有类似双曲正切函数的非线性特性[30],并具有更加丰富的状态响应.

在输出层,通过输出连接权值Wi与储备池内部虚节点状态xi的加权求和得到储备池计算的输出信号y(n),即:

由N个Wi构成的输出连接权值矩阵Wout在训练过程中通过伪逆算法计算获得

式中,X和Y分别为训练输入信号的虚节点状态矩阵和目标输出信号矩阵,其大小分别为M×N和M×1,M为训练样本的数据点数.

3 系统参数的选择

3.1 系统参数对偏振动力学特性的影响

固定宽带激光器的输出功率为4mW,VOA的衰减量为-0.54 dB.断开偏振动力学储备池计算系统实验装置的FC2 输出端与检偏器的连接,将其接入偏振分析仪(Santec 公司的PAM-10 偏振分析模块),观察不同SOA 工作电流下系统的输出功率和偏振度(degree of polarization,DOP),结果如图3 所示.从图3 可以看出,随着SOA 工作电流的增加,输出功率逐渐增加并趋于饱和,而输出光的DOP 先增加,后下降,近似在0—90%的范围内变化.这是由于随着SOA 电流增大,环形激光器由自发辐射过渡到了受激辐射,DOP 逐渐增加到最大;但随着SOA 电流持续增大,系统进入非线性状态,输出光的偏振态经历不同范围的快速波动,呈现在慢速的偏振分析仪上即为DOP 数值的减小[26];SOA 电流越大,光的瞬时偏振变化越剧烈,检测到的DOP 越小.不同输出偏振度对应的输出波形不同[27],也即储备池状态变量的不同.因此,不同电流下,SOA 光纤环形激光器储备池的偏振动力学响应的丰富程度不同.文献 [5]表明,SOA 工作在线性区时,基于SOA 光纤环形激光器的强度动力学RC 具有更好的任务处理性能.本研究证实,对于基于该环形激光器偏振动力学的RC,同样如此,故在后续实验中始终设置SOA 电流为67 mA,以使其工作在线性区.

图3 系统输出功率与偏振度随SOA 工作电流的变化Fig.3.Output power and DOP of the system vs.current of SOA.

除了SOA 工作电流,宽带激光器输出功率(对应于外部注入光功率)以及光纤环中VOA 的衰减量(对应于反馈增益)也对系统的输出光偏振度有影响,在本文实验所使用的硬件条件下测得的实验结果如图4 所示.尽管DOP 随着系统参数的改变而连续变化,但图4 中只采集了部分参数值下的DOP.由图4 可以看出,在宽带激光器输出功率较小情况下,随着光纤环中的衰减量逐渐增大,系统输出光的偏振度逐渐减小,这是由于光纤环中传输的光功率随着VOA 衰减量增大而减小,此时环形激光器处于SOA 的自发辐射状态.而随着宽带激光器输出功率的增加,反馈入SOA 的光功率也增加,环形激光器开始进入受激辐射状态,系统输出光的偏振度逐渐增大.不同宽带激光器输出功率和VOA 衰减量下,输出光偏振度不同,即SOA 光纤环形激光器储备池的工作状态不同,其偏振动力学响应的丰富程度也不同.因此,偏振动力学储备池计算系统工作点的选取,需着重考虑宽带激光器输出功率和光纤环中VOA 的衰减量的选择.结合图4中输出光偏振度随VOA衰减量的变化情况,本文主要选择VOA衰减量为-0.54,-1.74,-7.78dB进行分析,分别作为偏振度较大、适中和较小的情形,通过调整SLED 输出光功率,可使系统输出光DOP 在最大范围内变化.

图4 系统输出偏振度随宽带激光器输出功率及VOA 衰减量的变化Fig.4.Output DOP of the system vs.output power of SLED and attenuation of VOA.

3.2 系统参数对偏振动力学储备池属性的影响

储备池一般具备以下几个关键特性,才能有效地处理信息[31].首先是高维和非线性,即能把输入信号非线性映射到高维状态空间,将分类任务中不可线性分离的输入信号转换为可线性分离的输入信号,并有效地提取预测任务中输入信号的时空依赖性和非线性依赖性;其次是渐衰记忆(也被称为回声状态属性[1,2]),即储备池的节点状态是由当前输入信号和过去输入信号共同决定的,过去时间越久,对当前信号状态影响越小,这种对过去输入信号的衰落记忆对于处理具有短期依赖关系的时间序列是至关重要的;最后是可重复性和分离性,即RC 对相似的输入信号应该具有相近的储备池状态,以便将其分类到同一类中,不同类别的输入信号应该表现出足够不同的动力学响应,以便将其划分为不同类别.

接下来,对偏振动力学储备池计算系统的基本属性进行实验分析.将宽带激光器输出功率设置为4mW,VOA衰减量设置为-1.74dB,使用信号发生器产生一个周期为1 MHz、幅度为1 Vpp(峰峰值电压,voltage peak-peak)的正弦信号加载到强度调制器,观察系统的输出,可以直观地展示偏振动力学和强度动力学储备池计算系统的渐衰记忆和非线性响应,如图5 所示.图5(a)为系统的偏振动力学响应,图5(b)为系统的强度动力学响应.由图5 可见,除强度调制直接引起的响应变化之外,每隔一个反馈时延会出现一个幅度明显减小的响应变化,这是系统渐衰记忆的表现.强度调制直接引起的响应变化中,高电平引起的响应变化小于低电平引起的响应变化(参见图5 插图),且两种系统的高低电平输出响应具有相同的不对称性,这是由于系统的非线性都是由SOA 的饱和效应[5]引起的.

图5 系统的渐衰记忆和非线性响应 (a) 偏振动力学响应;(b) 强度动力学响应Fig.5.Fading memory and nonlinear response of the system: (a) Polarization dynamic response;(b) intensity dynamic response.

实验发现,偏振动力学RC 的渐衰记忆与光纤环中VOA 衰减量相关联.使用信号发生器产生一个脉宽为1 μs 的脉冲信号加载到强度调制器,固定宽带激光器输出功率为4 mW,研究了不同VOA 衰减量情况下,偏振动力学储备池计算系统的渐衰记忆(回声状态波形)的变化情况,并与系统的强度动力学状态输出作对比,实验结果如图6 所示.其中,图6(a)为系统的偏振动力学响应,图6(b)为系统的强度动力学响应.从图6 可看出,随着光纤环中VOA 衰减量的增大,偏振动力学储备池和强度动力学储备池的渐衰记忆先增强后减弱.这是因为VOA 衰减量较小时,环中光强较大,激光器主要受光反馈作用影响,外部输入光信号对激光器的影响较弱,输入信号在环中环行若干次后逐渐减小,显示记忆能力较弱;随着VOA衰减量增大,环中光强逐渐减小,光反馈作用减弱,输入光信号对激光器的影响逐渐增强,外部输入信号在环中环行多次才逐渐减弱,显示记忆能力较强;VOA 衰减量再增大,环中光强变得更弱,环形激光器中光注入效果远大于光反馈作用,输入信号环行1 次就衰减到很小了,显示记忆能力较弱.记忆能力的变化是光注入和光反馈作用博弈的结果.当VOA衰减量为-1.74dB时,两种动力学储备池计算系统都明显地具有更长久的渐衰记忆,处理对记忆能力有较高要求的任务将具有更好的性能.所以,可以根据所处理任务对记忆能力的要求,相应地调整VOA 衰减量,即调整反馈增益的大小.但在相同的宽带激光器输出功率和VOA 衰减量下,偏振动力学储备池和强度动力学储备池的渐衰记忆有差异,这将直接导致二者网络性能的差异.特别是,当VOA衰减量为-1.74dB时,两种动力学储备池计算系统的回声状态波形幅值变化趋势有明显差异,这表示两种系统呈现不同的回声状态属性,将在后续任务的处理中得以体现.

图6 系统的渐衰记忆随VOA 衰减量的变化 (a) 偏振动力学响应;(b) 强度动力学响应Fig.6.Fading memory of the system vs.attenuation of VOA: (a) Polarization dynamic response;(b) intensity dynamic response.

本文采用一致性评估偏振动力学储备池的可重复性,并通过调制光注入下两次不同时间采集的系统输出信号的互相关值来量化表示.以0.5 作为判别的阈值,如果两次输出信号的互相关值大于0.5,则该系统具有一致性,否则没有获得一致性.分离性通过相同系统参数下两组不同类型输入信号下采集的系统输出信号的互相关值来量化表示.同样以0.5 作为阈值,但当两次输出信号的互相关值小于0.5 时,判别该系统具有分离性,否则没有获得分离性.互相关值的计算公式[32]为

式中,Ci,j为两次输出信号的互相关值;Ii和Ij分别为两次输出信号;和分别为两次输出信号的平均值;σi和σj分别为两次输出信号的标准差;〈·〉表示计算平均值.

调整宽带激光器的输出功率和VOA 衰减量,观察两种动力学储备池计算系统一致性的互相关值和分离性的互相关值随系统参数的变化情况,结果如图7 所示.图7(a)显示了系统一致性随宽带激光器输出功率和VOA 衰减量的变化情况.两种动力学储备池计算系统的一致性随两个参数的变化趋势区别不大.VOA 衰减量较大时,系统获得较好的一致性,互相关值在0.9 以上;此时,反馈的光功率相对较小,减少了反馈的不稳定性,使系统的一致性较好.在相同VOA 衰减量情况下,系统一致性基本保持稳定,反映了外部光注入功率的变化对系统工作状态的影响较小.图7(b)显示了系统分离性随宽带激光器输出功率和VOA 衰减量的变化情况.两种动力学储备池计算系统的分离性实验结果相差不大.在不同VOA 衰减量下,两种动力学储备池计算系统的分离性一直保持在较好水平.

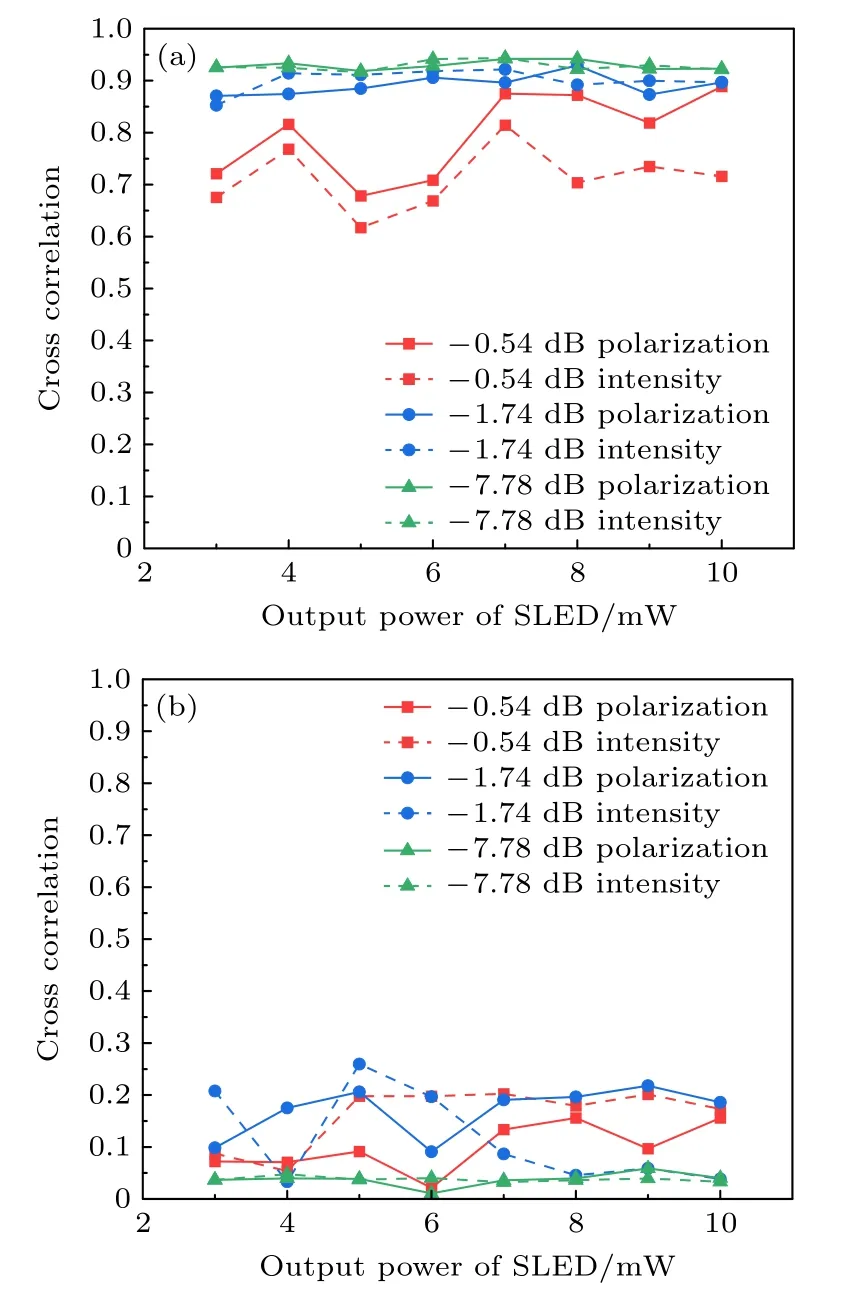
图7 系统的一致性和分离性随宽带激光器输出功率和VOA 衰减量的变化 (a) 一致性的互相关值;(b) 分离性的互相关值Fig.7.Consistency and separation of the system vs.output power of SLED and attenuation of VOA: (a) Cross correlation of the consistency;(b) cross correlation of the separation.

结合系统一致性和分离性分析,VOA衰减量为-7.78 dB时,系统的一致性和分离性较好并保持平稳,此时外部注入光功率作用明显大于环内光反馈作用.系统较好的一致性和分离性来源于强外部光注入的效果,表现在图6 中为渐衰记忆的降低.这种情况下,虽然没有较长的渐衰记忆,但处理记忆能力要求较低的任务依然可以获得很好的性能.

综上所述,当VOA 衰减量较大(≥-1.74 dB)时,宽带激光器输出功率对偏振动力学储备池基本属性影响不大,此时,偏振动力学储备池具有更长的渐衰记忆,能很好地处理对记忆能力有较高要求的任务;并且储备池具有更好的一致性和分离性,处理识别任务能够获得较好的性能.VOA衰减量增大到一定数值(如-7.78dB)后,偏振动力学储备池的渐衰记忆下降,此时,偏振动力学储备池只适用于处理对记忆能力要求不高的任务.但VOA衰减量设置为-7.78dB时,偏振动力学储备池的一致性和分离性最好,所以,处理对记忆能力要求不高的任务时,VOA衰减量设置为-7.78dB比较合适.另外,两种动力学储备池的基本属性相近,预示着两种动力学储备池的性能相当.

4 预测与分类任务的处理结果

4.1 Santa Fe 时间序列预测任务

使用Santa Fe 时间序列预测任务来评估系统的预测性能.Santa Fe 时间序列预测任务的目的是对混沌时间序列的提前一步预测.Santa Fe 时间序列包含9000 个数据点,是由在混沌状态下工作的远红外激光器产生的[33].在本研究中,使用前3000 点数据进行训练,接下来的1000 点数据进行测 试.使用归一化均方误差(normalized mean square error,NMSE)来量化预测性能,NMSE 被定义为

式中,L为测试样本的数据长度,y(n)为储备池计算系统的实际输出,(n) 为目标输出;var()为目标输出的方差.当NMSE 的值小于0.1 时,表示储备池计算系统有好的预测性能.

图8 展示了在宽带激光器输出功率为10mW和V OA 衰减量为-7.78dB下获得的偏振动力学储备池计算系统处理该任务的结果.储备池中虚节点数设置为30,缩放因子设置为1,掩码信号采用[0,1]内均匀分布的随机信号.图8(a)展示了掩码后的测试输入信号及系统的偏振动力学响应.偏振动力学RC 系统的预测结果如图8(b)所示,其中,上面板为目标信号(即原始信号)和预测结果,下面板为目标信号和预测信号之间的误差.由图8(b)可见,预测信号与目标信号相似度很高,NMSE 为0.0058.

图8 Santa Fe 时间序列预测任务的信号波形 (a) 掩码后的输入信号和偏振动力学响应;(b) 预测结果Fig.8.Signal waveforms of Santa Fe time series prediction task: (a) Masked input signal and polarization dynamic response;(b) prediction results.

为了研究外部注入光功率对偏振动力学RC系统预测性能的影响,并将其与强度动力学RC 系统进行比较,在不同的VOA 衰减量下,改变宽带激光器输出功率,分别考察了两种动力学RC 对Santa Fe 时间序列的预测性能,结果如图9 所示.从图9 可以看出,在各组参数下两种储备池计算系统处理该任务的网络性能都相当,且NMSE 均处于0.1 以下,表明偏振动力学RC 同强度动力学RC一样具有良好的预测性能.但VOA 衰减量较小时,预测性能受宽带激光器输出功率的影响较大,因为此时系统的一致性和分离性受宽带激光器输出功率的影响就比较大,参见图7.

图9 预测性能随宽带激光器输出功率的变化 (a) 偏振动力学RC 测试结果;(b) 强度动力学RC 测试结果Fig.9.Prediction performance vs.output power of SLED: (a) Polarization dynamics RC testing results;(b) intensity dynamics RC testing results.

进一步探究缩放因子γ和虚节点数N对偏振动力学RC 系统预测性能的影响,并与强度动力学RC 的进行对比,实验结果如图10 所示.两种动力学RC的预测性能变化趋势基本一致.在SLED输出光功率为4mW,VOA衰减量为-7.78dB情况下,当N=30 时测得两种动力学RC 的预测性能随缩放因子γ的变化情况,如图10(a)所示;当γ=1 时测得两种动力学RC 的预测性能随虚节点数N的变化情况,如图10(b)所示.由图10(a)可见,NMSE 始终处于0.1 以下,即不同的γ情况下,两种动力学RC 均具有良好的预测性能;另外,NMSE 随着γ的增大呈现先减小后增大的趋势,γ处于1.2 附近时,系统可以获得更好的任务处理性能.图10(b)显示,N≤ 90 时,系统始终具有良好的预测性能;N＞90 时,由于虚节点数过多导致过拟合,此时系统处理Santa Fe 时间序列预测任务的性能迅速下降.

图10 预测性能随缩放因子(a)和虚节点数(b)的变化Fig.10.Prediction performance vs.scaling factor (a) and number of virtual nodes (b).

4.2 多波形识别任务

使用一个多波形识别任务来评估偏振动力学RC 系统对不同信号进行分类的性能.该任务目标是正确地分类随机连接的波形,包括正弦波、方波、三角波,如图11(a)所示.在输入层中,首先将每周期波形离散为25 个点,这25 点数据构成的向量乘以维数为25×N的掩码矩阵(N为虚节点数)得到1×N的掩码后输入信号(如图11(b)所示).再将输入信号以T为周期连续输入到储备池中.在输出层中,使用1 个线性分类器.分别将正弦波、方波和三角波信号的类别标签对应于“0”,“1”和“2”,即它们的目标输出,如图11(c)所示.在本研究中,使用2000 个周期的波形进行训练,1000 个周期的波形进行测试.通过识别率(identification rate,IR)对其识别性能进行定量评价.IR 被定义为:

图11 多波形识别任务的信号波形 (a) 原始信号;(b) 掩码后的输入信号;(c) 目标输出信号的局部放大;(d) 目标输出信号;(e) 实际输出信号Fig.11.Signal waveforms of multi-waveform recognition task: (a) Original signal;(b) masked input signal;(c) locally amplified target output signal;(d) target output signal;(e) actual output signal.

式中,Nt为测试波形样本的总数;Nc为正确识别的波形样本数.

图11(d)和图11(e)展示了在宽带激光器输出功率为3mW和VOA 衰减量为-7.78dB 下获得的偏振动力学RC 处理该任务的结果.储备池中虚节点数也设置为30,缩放因子为1,但掩码信号采用[-1,1]内均匀分布的随机信号.图11(d)为目标输出信号,图11(e)为储备池计算系统的实际输出信号,在这种参数情况下,系统可100%正确识别出三种波形.

图12(a)和图12(b)分别为使用偏振动力学RC和强度动力学RC 处理多波形识别任务的性能随宽带激光器输出功率的变化情况.从图12 可以看出,在相同参数情况下,两种动力学储备池计算系统的识别性能也相当.值得注意的是,当光纤环中VOA衰减量为-1.74dB时,偏振动力学RC的识别性能优于强度动力学RC 的,这是因为此时偏振动力学储备池的渐衰记忆比强度动力学储备池的衰减得更快,参见图6,这对分类任务是有利的,且偏振动力学储备池不易受系统强度噪声的影响.

图12 识别性能随宽带激光器输出功率的变化 (a) 偏振动力学RC 实验结果;(b) 强度动力学RC 实验结果Fig.12.Recognition performance vs.output power of SLED: (a) Polarization dynamics RC experiment results;(b) intensity dynamics RC experiment results.

图13 呈现了缩放因子γ和虚节点数N对偏振动力学RC 系统分类能力的影响,并与强度动力学RC 的进行对比.两种动力学RC 的分类能力变化趋势基本一致.在SLED输出光功率为4 mW,VOA衰减量为-7.78dB情况下,当N=30 时测得两种动力学RC 的分类能力随缩放因子γ的变化情况,如图13(a)所示;当γ=1 时测得两种动力学RC 的分类能力随虚节点数N的变化情况,如图13(b)所示.由图13(a)可见,γ＜ 1 时,IR 随着γ增大而增大,γ≥ 1 时,IR 始终高达100%.图13(b)显示,N≤ 90 时,系统始终具有良好的分类能力;N＞ 90 时,由于虚节点数过多导致过拟合,此时系统处理多波形识别任务的性能迅速下降.

图13 分类能力随缩放因子(a)和虚节点数(b)的变化Fig.13.Classification capability vs.scaling factor (a) and number of virtual nodes (b).

5 结论

本文提出了一种基于偏振动力学的储备池计算系统.其主要结构为SOA 光纤环形激光器,输入信号通过强度调制方式注入储备池中.该系统以SOA 作为非线性节点,以系统的偏振动力学状态响应作为储备池内部变量.通过实验分析了偏振动力学状态响应的影响因素,并结合储备池的渐衰记忆、非线性、一致性和分离性,指出了系统参数的选取范围.偏振动力学RC 系统在Santa Fe 时间序列预测任务和多波形识别任务中取得了较好的实验结果;与强度动力学RC 相比,两种动力学RC 系统处理任务的性能相当,但基于偏振动力学的RC 系统不易受系统中SOA 自发辐射噪声的影响.非线性系统的偏振动力学作为储备池状态响应具有较大的发展潜力.

另外,若同时利用半导体光纤环形激光器的强度动力学响应和偏振动力学响应作为储备池状态变量,则有望实现并行任务处理,我们已开展了进一步的研究[34].