基于频谱Sevcik维数的目标运动速度估计*

赵晓静 高大治 孙 凯 李玉征 郭豆豆

(中国海洋大学信息科学与工程学部 青岛 266100)

0 引言

线谱具有能量高、传播距离远等特点[1]，被广泛应用于目标运动参数估计。线谱多普勒频移包含着目标的运动速度、到达最近点时间、最近距离等运动参数信息。1994年，Ferguson 等[2]提出了利用线谱多普勒频移估计目标运动参数的方法，该方法利用时频分析获取瞬时频率，与多普勒频移模型进行拟合，获取目标的运动参数。而后，Quinn[3]推导了接收器和运动声源运动方向不共线时多普勒频移表达式。邹红星等[4]提出了Dopplerlet 变换，该变换可将多普勒频移去除。吴国清等[5]利用邹红星等提出的Dopplerlet 变换和匹配投影算法，提取线谱多普勒中包含的目标速度和最近距离等运动信息，而后又提出了一种利用多线谱的多普勒频移估计运动目标最近距离的方法[6]，先用Wigner-Ville分布提取瞬时频率，再定义多普勒频移的基函数，实现目标的运动参数估计。该方法的缺点是需要大量的先验知识。高伟等[7]提出了一种基于目标噪声辐射强度和线谱多普勒频移估计目标最近距离的方法，该方法不需要大量的先验知识，且搜索范围易确定。徐灵基[8]针对水下目标线谱多普勒进行深入研究，通过引入了一种时频变换–匹配Wigner变换，获取多普勒频移，从而实现目标运动参数估计。Liang[9]等提出了Doppler-Chirplet 变换，该变换直接利用观测到的瞬时频率与源速度的关系作为Chirplet 变换的核心，可直接估测运动目标的速度。同时，还有多尺度Chirplet 路径追踪方法[10]等。刘凯悦等[11]提出了一种基于线谱多普勒的水下对空中声源的运动参数获取方法。这些算法不仅提高了计算精度，也缩短了计算时间。现有的基于多普勒频移获取运动参数大都基于瞬时频率。高德洋等[12]提出了一种不需要提取瞬时频率的线谱目标运动参数获取方法，他首先提出Doppler-warping变换，将warping 变换的思想运用到多普勒频移的去除上，又利用频谱求熵的方法获取目标的运动参数，相较于Ferguson 等的算法，不需要提取瞬时频率，因此适用性更高，计算精度也更高。

分形维数与熵一样，都是表征系统复杂程度的物理量。因此，分形维数在信号处理方面有广泛的应用。现阶段，分形维数被广泛应用于图像分类[13-14]、故障诊断[15]、地形分析[16]、频谱感知[17-18]等方面。截至目前，鲜有学者将分形维数应用于线谱信号目标运动参数估计中。本文将频谱分形维数应用到目标运动速度获取中。首先利用Doppler-warping变换对接收信号重采样，然后通过计算频谱的分形维数作为衡量多普勒频移消除程度的代价函数，最后通过获取代价函数最小值对应的速度值获取目标的运动速度。

1 理论

1.1 多普勒频移及Doppler-warping变换

当声源沿不经过接收器的路径做匀速直线运动时，接收器接收信号存在多普勒频移，其运动示意图如图1 所示。其中v为目标声源的运动速度，t0为到达最近点时间，r0为最近距离，接收信号瞬时频率由Quinn[3]推导的表达式得出，如式(1) 所示：

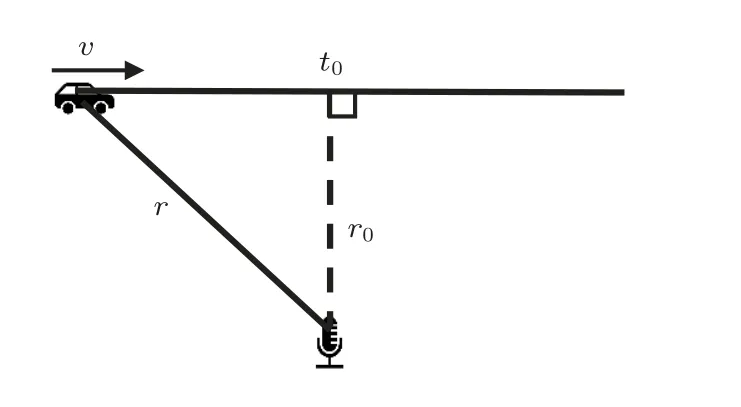
图1 声源与接收器运动示意图Fig.1 Geometrical model of the wayside acoustic testing model

其中，f0为目标声源发射信号的频率。本文中，设置t0、r0已知，搜索目标匀速直线运动速度v。由式(1)可以看出，由于多普勒效应的存在，接收信号的频率不再为单频，而是随时间变化的。

Doppler-warping 变换由中国海洋大学水声研究团队[12]提出，warping 算子的表达式如式(2)所示：

使用式(2)对接收信号进行重采样，即将式(2)代入式(1)的t中，经整理后f(t)=f0，具体推导过程见文献[12]。此时多普勒频移被消除，原始信号的单频特性恢复。接收信号经过Doppler-warping 变换前后，LOFAR图如图2所示。

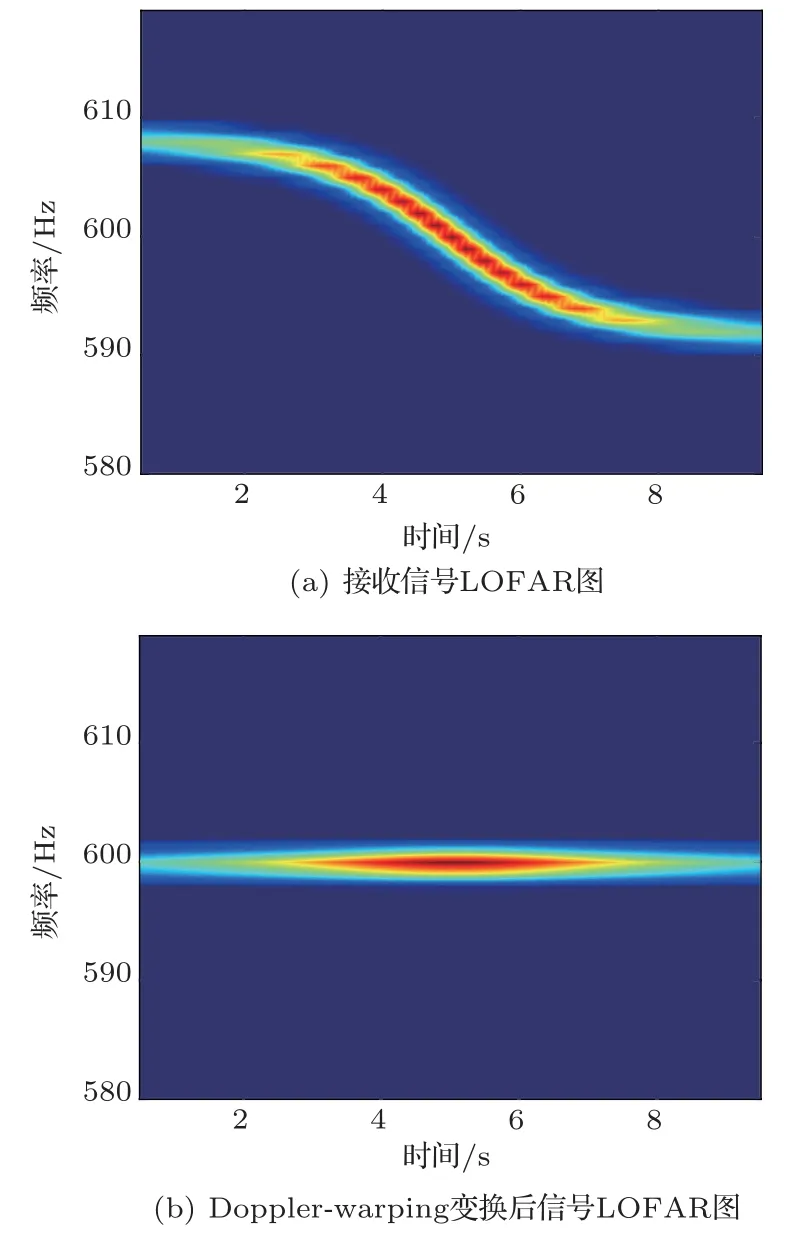
图2 接收信号Doppler-warping 变换前后Fig.2 LOFAR figure of single-frequency signal and LOFAR figure after Doppler-warping transform

1.2 Sevcik维数

分形维数是衡量事物分形特性的一种度量参数，也是衡量事物复杂程度的物理量。分形维数主要可分为Katz 分形维数、Hausdorff维数、计盒维数、Sevcik 分形维数和自相似分形维数等几种。其中，Sevcik 维数多用于衡量信号的波形的分形特性，且计算过程较简单，计算时间短。因此，本文采用Sevcik 维数来衡量信号频谱的分形特性。Sevcik 维数的表达式如式(3)所示：

其中，N为信号点个数，L为信号波形长度，其表达式如式(4)所示：

对于一个时域信号s(t)，若其时长为T，采样率为fs，信号点个数为N，则其经过快速傅里叶变换(Fast Fourier transform,FFT)后，频谱S(f)的xk对应信号频率点fk。此时其信号波形长度L的表达式经整理后如式(6)所示：

1.3 算法步骤

由于多普勒的存在，线谱信号的频谱能量不再集中在原始频率上，而是在中心频率周围有一定的展宽，此时，信号频谱的分形维数会比不存在多普勒时明显升高，通过Doppler-warping 变换后，可将多普勒频移去除，此时信号恢复单频特性，其频谱的分形维数会明显降低。Doppler-warping 算子中包含最近点时间、最近距离、速度等运动参数，因此，Doppler-warping算子中运动参数的准确性影响多普勒的去除程度。可通过线谱和连续谱结合的方式，估计目标到达最近点的时间和最近距离，本文假设以上两参数已知，利用Doppler-warping 变换结合频谱Sevcik 维数单独进行速度估计，其步骤可概括为以下几步：

(1)设置速度搜索网格[v1,v2,···,vk]。应用时，可根据需要设置速度搜索步长，在常见目标速度估计应用中可将搜索步长设为0.1 m/s。

(2) 最近点时间和最近距离两参数由其他方法估计，设为已知，计算每个速度值下的Dopplerwarping算子。

(3) 将不同算子代入接收时域信号s(t)，对接收信号进行重采样，获得信号s′(t)。

(4) 对s′(t)进行傅里叶变换后获得频谱S′(f)，取模并计算每一个S′(f)的Sevcik分形维数D(vk)。

(5) 找到D(vk)取值最小时对应的速度v，即为速度估计值。

算法流程图如图3所示。

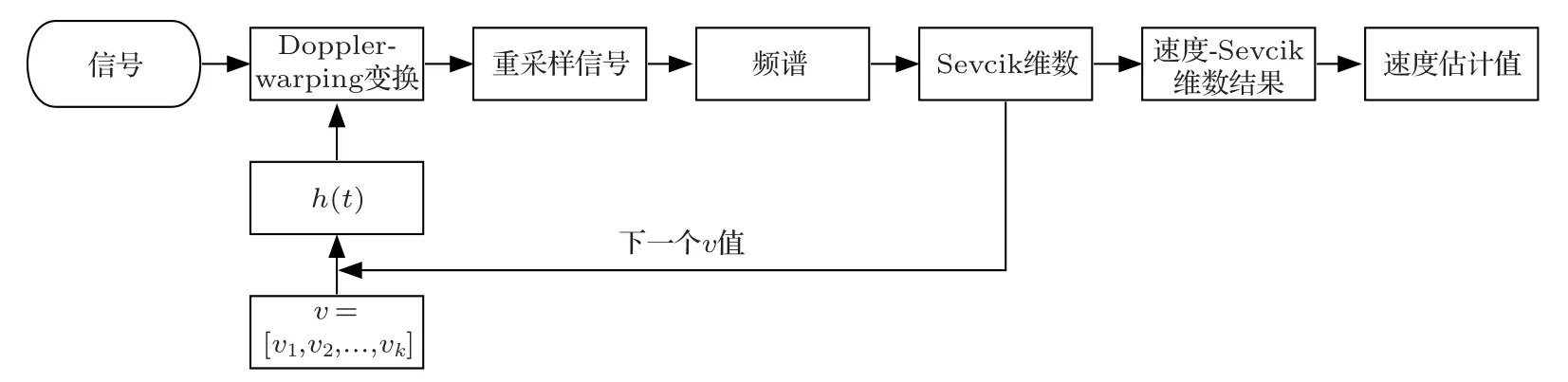
图3 算法流程Fig.3 Flow chart of the algorithm

2 仿真及算法性能

2.1 仿真及结果

基于以上理论，进行仿真验证，本文算法对空气中目标和水中目标同样适用，这里以空气中目标为例。声源信号为600 Hz 单频信号，采样率为10000 Hz，信号时长10 s。声源运动速度为10 m/s，最近距离为10 m，最近点时间为5 s。声速为340 m/s。接收信号及处理结果如图4所示。

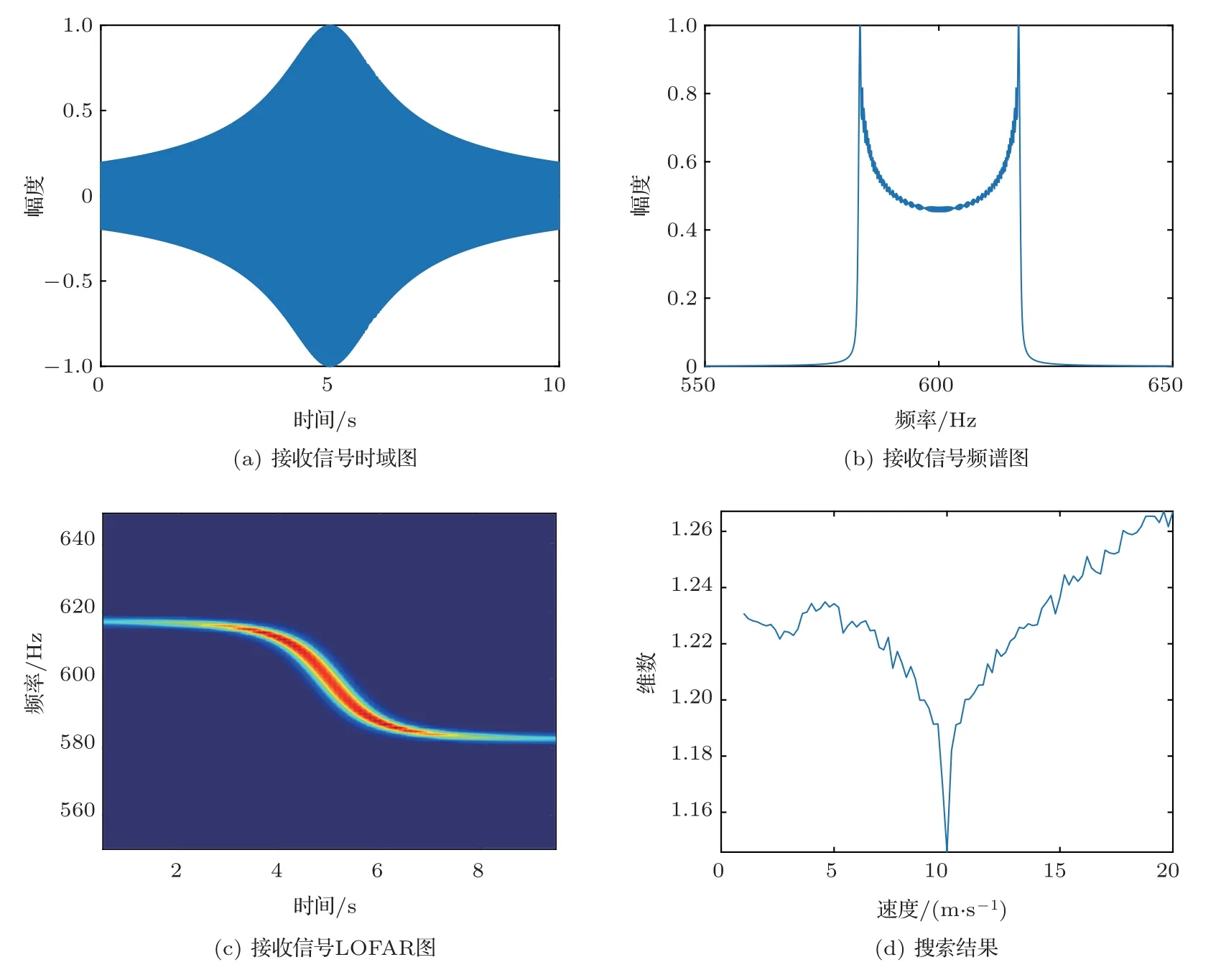
图4 仿真结果Fig.4 Simulation results

设置速度搜索网格为[1 : 0.2 : 20]，搜索速度v，结果如图4(d)所示。

利用本文方法进行搜索速度，从图4(d)可以看出，在真实速度值10 m/s 处，Sevcik 维数明显低于错误值处，因此能准确搜索出速度结果，证明本文提出的方法有效。

2.2 算法性能

为了体现本文提出算法的性能，与用熵作为代价函数的搜索结果进行比较。在相同的仿真条件下，分别用熵作为代价函数和Sevcik 维数作为代价函数，进行速度估计。估计结果如图5所示。

图5 熵和Sevcik 搜索结果对比Fig.5 Comparision of estimation result of entropy and Sevcik

由于本文算法是寻找代价函数最小值，因此定义最小代价函数值为0 dB，定义3 dB 处对应的两速度值的差为主瓣宽度。根据以上定义，用Sevcik维数作为代价函数时，主瓣宽度为0.76 m/s，而用熵作为代价函数，主瓣宽度为3.81 m/s。可见用Sevcik维数和熵作为代价函数时，虽然都可以搜索出正确速度值，但是本文提出的算法，搜索结果在正确值位置处起伏更明显，瓣更窄，性能更好。

在实际应用中，往往接收信号存在噪声，有时甚至信噪比(Signal to noise ratio,SNR) 很低，因此，本文利用仿真分析不同SNR下两种算法的性能对比。仿真条件为：信号时长20 s，声源运动速度为10 m/s，最近距离为10 m，最近点时间为10 s。分别在仿真的接收信号中加入高斯白噪声，SNR计算方法采用谱SNR。两种算法搜索结果对比如图6 和表1所示。

表1 典型SNR 下两方法速度估计误差对比Table 1 Comparison of speed estimation errors between the two methods under typical SNR

图6 SNR 对两种算法搜索结果的影响Fig.6 Influence of SNR on the two algorithms

从图6 和表1 中可以看出，在仿真条件相同的情况下，SNR 过低时，Sevcik 维数和熵作为代价函数效果均不佳，这是因为当SNR 较低时，噪声对信号频谱有较大影响，因此两种方法均会失效。但是，从图6 可以看出，Sevcik 维数作为代价函数抗噪性提高5 dB 左右。主要原因是两种算法都基于频谱的混乱程度，即使在SNR 低于-5 dB 的情况下，多普勒的存在与否也会对频谱的Sevcik 维数产生较大影响，即存在多普勒时频谱的Sevcik 维数明显大于不存在时，因此本文算法可行。而只有在SNR大于-5 dB 以后，用熵值作为代价函数时，多普勒的存在与否对频谱的影响较大，熵值作为代价函数的算法才会有效。SNR 对多普勒是否存在时两种不同代价函数的影响如图7(a)、图7(b)所示。在相同SNR下，多普勒的存在对频谱Sevcik维数的影响明显大于频谱熵(如图7(c)所示)。

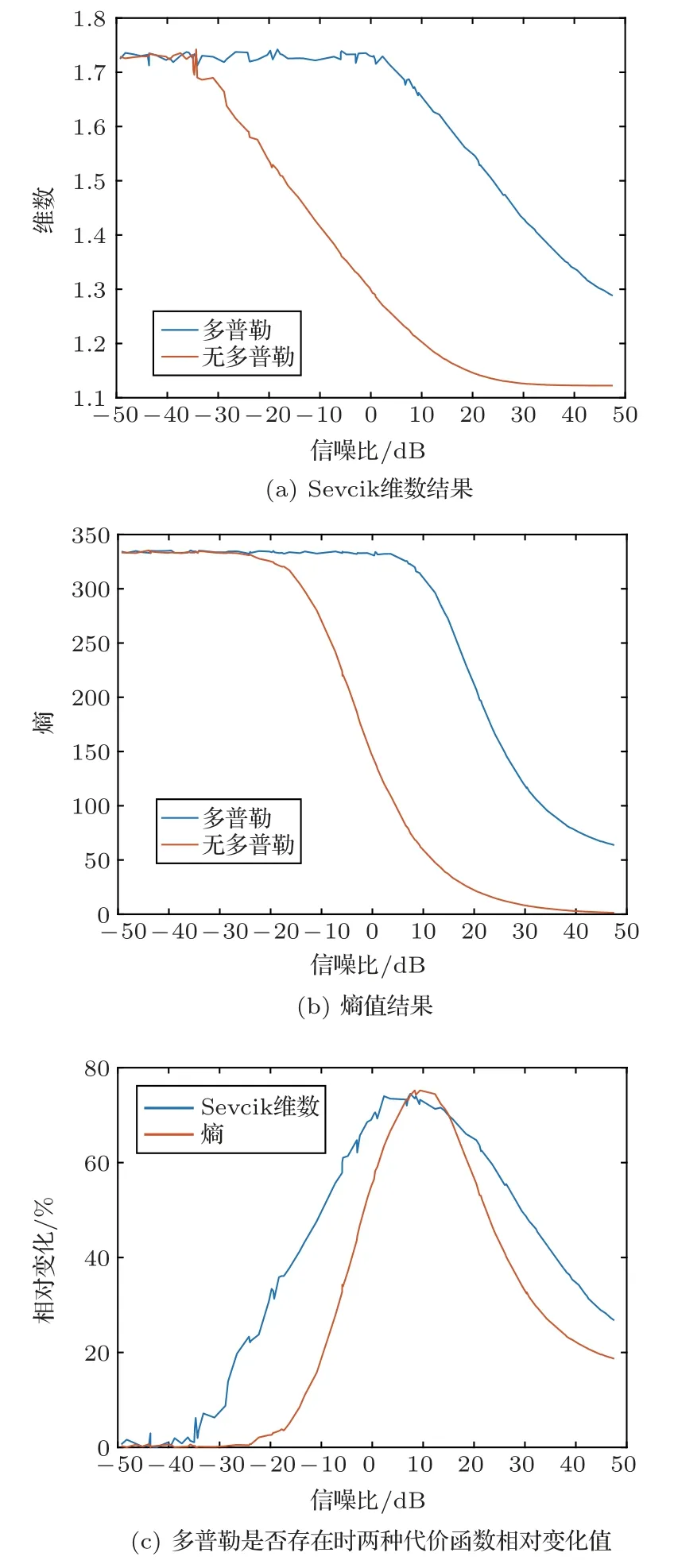
图7 SNR 对多普勒是否存在时两种代价函数的影响Fig.7 The effect of the SNR on the presence or absence of Doppler on the two cost functions

3 实验及结果

3.1 实验

针对上述理论和仿真结果，进行实验。陆面目标采用某卡车运动过程中辐射的线谱噪声，数据来源为acousticstoday.org。该信号时长30 s，采样频率为12000 Hz。声速为347 m/s。最近距离为35 m，速度为20 km/h。其到达最近点时间为15.2 s，本文在处理过程中将其设为已知量。接收信号LOFAR图以及搜索结果如图8所示。

图8 卡车实验结果Fig.8 Truck experiment results

图8(a)为接收器接收信号LOFAR 图，该图中线谱多普勒十分明显。设置速度网格为[1:0.1:15]，单独搜索速度的结果如图8(b)所示，结果为5.8 m/s，相对误差仅为4.4%，该结果证明了本文算法的有效性。本文方法与熵值方法搜索结果对比如图8(c)所示。计算两种算法速度搜索结果的主瓣宽度，熵值算法的主瓣宽度为3.15 m/s，本文算法的主瓣宽度仅为0.74 m/s，结果表明本文算法主瓣宽度明显更窄。

为了进一步证明本文算法的有效性，选取2022年6 月在青岛近海进行的海试实验数据，实验声源为航道上经过的货轮，该目标为非合作目标，货轮的运动轨迹经接收船船载AIS(船舶自动识别系统)记录如图9(a)所示，距离变换如图9(b)所示。接收信号为货轮在运动过程中辐射线谱噪声。实验地声速为1510 m/s，选取的信号时长为1200 s，信号采样频率为80000 Hz。由于信号采样率过高，而处理信号所选线谱频段仅为980～1000 Hz 左右，因此对接收信号进行降采样以减少计算量。接收信号频谱图和LOFAR 图如图9(c)、图9(d) 所示。货轮运动平均速度为5.3 m/s，到达水听器最近距离为2010 m，选取的信号中，目标到达最近点的时间为49 s。利用本文提出方法进行运动速度搜索，搜索结果如图9(e)所示。设置速度网格为[1:0.1:10]，速度搜索结果为5.1 m/s，相对误差仅为3.8%。本文算法和熵值算法速度搜索对比结果如图9(f)所示。计算两种算法的主瓣宽度，熵值算法的主瓣宽度为1.31 m/s，而本文算法的主瓣宽度仅为0.28 m/s，因此本文算法的性能较熵值算法有明显提高。

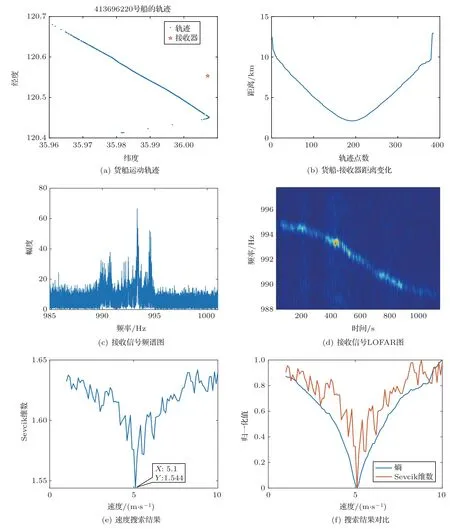
图9 海试实验结果Fig.9 Marine experiment results

以上两组实验结果误差分别为4.4%和3.8%，均能较为准确估计目标运动速度值，速度搜索相对误差均小于5%。两组实验结果均证明了本文提出算法的有效性。

4 结论

本文提出了Doppler-warping 变换结合频谱分形维数的方法来获取目标的运动速度。传统方法通过迭代算法提取接收信号的瞬时频率，计算时间较长，本文提出的算法过程简单，计算时间较短。相对于用熵作为衡量频谱复杂度的代价函数，本文利用Sevcik维数作为代价函数，经仿真检验，抗噪能力较熵值方法提高5 dB。经仿真和实验检验，本文算法代价函数主瓣宽度更窄，具有更好的性能。空气和水中声目标实验均可准确搜索出目标运动速度，两实验误差均小于5%，证明了本文所提算法的有效性。下一步拟将本文方法用于宽带噪声目标和双目标的运动参数获取中，实现算法应用的扩展。