非均匀流体介质内部散射声场重建的逐层计算方法*

唐少杰 向 宇 石梓玉

(1 广西科技大学 广西汽车零部件与整车技术重点实验室 柳州 545006)

(2 广西科技大学机械与汽车工程学院 柳州 545006)

0 引言

超声层析成像广泛应用于生物医学、无损检测、地球物理等领域[1-5]，其基本原理是利用超声波照射物体，由外部超声散射场求解物体内部结构，亦可称为逆散射问题。对于流体介质内部的散射声场的求解，即已知介质内部结构，由对比度函数求解介质内部散射声场分布，以往采用矩量法(Method of moment,MoM)求解上述问题。MoM 的相关研究最早可追溯至20 世纪60年代，Richmond[6-7]采用MoM 精确描述了微波通过二维介质时的散射场。随后，Johnson 等[8]将MoM 应用于超声前向散射问题中。自此MoM 在超声技术中获得广泛应用[9-12]。但在超声问题中，为获得较高分辨率，入射声波频率常取200 kHz 以上，且为得到良好的计算精度，需在一个波长内划分3～10个单元，由此所得网格密度极大，若此时采用MoM 离散整个求解域将形成大规模矩阵，普通计算机算力难以求解，限制了其在实际中的应用。

国内外学者为使MoM 适用于大规模问题提出了一系列改进方法，通常分为两类。第一类以快速多极子算法及多层快速多级子算法为代表[13-16]，该类算法将MoM中“点对点”的直接运算通过中间变换和传递分解划分为“块对块”的间接计算，并采用迭代求解器求解线性方程组以避免显式生成系数矩阵，以此降低内存使用量与计算复杂度。第二类以亚全域基函数法[17]、特征基函数法[18]为代表，该类算法使用高阶基本函数离散向量积分方程，产生一个高度压缩的线性标量矩阵方程，大幅度减少了矩阵方程中的变量个数。

针对MoM 计算非均匀流体介质内部散射声场形成矩阵规模大进而对算力要求高的问题，本文结合声散射基本理论与近场声全息技术推导出逐层离散、逐层计算非均匀介质内部散射声场的理论公式，并给出对应的几何离散模型。在相同模型、条件下应用MoM 与逐层算法进行数值仿真，结果表明逐层算法可以有效重建流体介质内部散射声场并减小矩阵求解规模。

1 基本理论

当超声波入射非均匀流体介质时，由于散射作用，该介质成为次级声源，向四周辐射散射波。此时，空间任意点r的全场声压可由式(1)描述：

其中，p(r)、pin(r)和ps(r)分别为r处的全场声压、入射声压和散射声压。

式(1)满足非齐次亥姆霍兹方程[5]，可用Lippmann-Schwinger积分方程表示：

其中，S为非均匀流体介质存在区域；G(r,r′)是自由空间Green 函数，在二维问题中为(kd)[19-20]，其中的(kd)表示0 阶第2类Hankel 函数，d=‖r-r′‖，k为波数；o(r′)为像函数，是描述物体内部介质声学特性参数的函数，o(r′)=k2(n2(r′)-1)，n2(r′)-1 为对比度函数，n(r′)=c0(r′)/c(r′)，c0(r′)为背景介质声速，c(r′)为介质声速；散射场ps(r)表示为

以往使用MoM 离散计算区域简化求解过程。MoM 采用脉冲基和点匹配，将式(3)转化为代数方程组的形式，若介质内部结构已知，即各离散单元的像函数o(r′)已知，可求出空间任意点的全场与散射场。MoM 计算思路简单，易于编程实现，但更适用于低激励频率、单元大且少的问题，随着激励频率增高，网格划分逐渐密集，离散整个求解域S将形成极大规模的复数满秩矩阵，普通计算机已无法满足算力要求，不利于实际应用。

2 逐层算法

为克服MoM 上述缺陷，提出一种结合声散射基本理论与近场声全息技术逐层求解流体介质内部声场的计算方法。为便于计算，将介质存在区域拓展为规则形状(Region of interest,ROI)，若对该区域逐层离散、逐层求解，可逐步得到整个ROI 区域的声场分布。通过这种逐层计算方法，对比于MoM的矩阵求解规模明显减小。

假设ROI 区域可划分N层单元，由第1 节理论可知，计算第n层(n=1,2,···,N)任意单元处的全场，应由入射声源、前n-1 层已离散计算得到声场分布的单元声源、第n层所有单元声源及第n+1～N层暂未离散区域声源共同作用得到，求解计算层声场的关键在于表示未离散区域声源对计算层单元处的声场。因近场声全息技术可以匹配检测面上的信息重建声源外部声场，且无论是边界元法(Boundary element method,BEM)还是波叠加法(Wave superposition method,WSM)均可将全部已知量和待求量集中在边界或虚拟边界上，达到降维、简化计算的效果[19,21]，所以近场声全息技术可以应用于求解未离散区域声源对第n层单元处的声场计算问题。又因WSM 具有算法简单、计算效率高的优点，在近场声全息中得到了广泛应用，所以本文采用WSM求解上述问题。

2.1 WSM及其离散形式

WSM 基本思想是：在计算声源外部散射场时，次级声源向外散射的声场可由连续分布于其内部的虚拟源的声场叠加替代，虚拟源强可以通过匹配检测面的相关信息获取。如图1 所示，O为坐标原点；S0为散射声源真实边界；S′为置于散射声源内部的虚拟边界；Ωout为散射声源外部散射域；r′为虚拟边界上虚拟源的位置向量；r为Ωout区域内任意场点的位置向量。

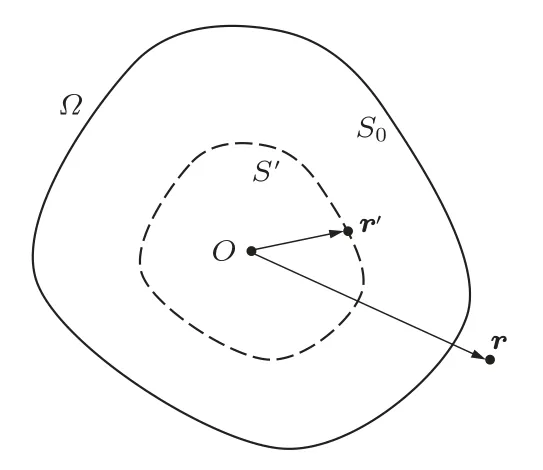
图1 WSM 示意图Fig.1 Diagram of WSM

声源外任意一点的全场为

其中，Q(r′)为虚拟源强；G(r,r′)为关于虚拟源和场点位置矢量的传递矩阵；散射场为

2.2 离散模型描述

逐层算法采用声全息的声场重构原理，为保证声场重建的稳定性，应将虚拟边界S′、声源边界S0与检测边界设置H为共形，又因检测边界常为圆形，所以本文将ROI区域、虚拟边界与检测边界均设置为圆形，如2 图所示。ROI 区域等宽划分N层，前N-1 层每一层划分M个矩形单元，第N层为1 个圆形单元。

如图2所示，将ROI区域划分为3个部分，S2与S1边界之间的区域为前n-1 层声源(已通过逐层缩进计算得到声场分布的区域)，记为A区域；S1与S0边界之间为第n层声源，记为B区域；S0边界以内为未离散区域，记为C区域，该区域声源对S0边界以外场点的散射声场可用式(5)表示；在ROI 区域外的圆形边界为声压检测边界。

图2 逐层算法几何离散模型示意图Fig.2 Diagram of layer-by-layer geometric discrete model

2.3 逐层计算算法

场点r处的全场应由A、B、C区域所有散射声源以及入射声源共同作用得到，式(6)可重写为

其中，pA(r)、pB(r)、pC(r)分别为A、B、C三个区域散射声源作用在C区域外任意点r处的声压。

A区域包含M×(n-1)个单元，在场点r处的声压为

B区域包含M个单元，在场点r处的声压为

为简化计算，将C区域中虚拟边界S′同样离散为M个单元，在场点r处的声压为

oA=diag(o())，表示由A区域单元像函数形成的(M×(n-1))× (M×(n-1))维对角阵；oB=diag(o())，表示由B区域单元像函数形成的M×M维对角阵；

整理式(11)可得C区域虚拟源的源强列向量QC表达式为

QC为仅关于pB的函数，其他参数均为已知。为得到pB，需将场点配于B区域每个单元中心：

联立式(12)、式(13)，整理得到pB表达式：

式(14)中，E为M×M维单位矩阵。

由此便得到了B区域所有单元的全场声压，计算出B区域声压分布后纳入区域A作为已知量，随着n增大。逐层内缩，重复上述过程即可得到声源内部即ROI区域所有单元的声场分布情况。需注意因WSM计算时声源边界S0内部存在虚拟面S′，因此计算层最大值nmax不能取到ROI 区域最内层，nmax大小为当虚拟面取到ROI 区域最内层时的计算层n。此时还未求解的总规模相比整个ROI区域规模非常小，可直接使用MoM 计算，具体计算过程不加以赘述。

特殊的，当n=1 时，ROI 区域仅由B、C区域组成，此时在检测面H上配点可得pH为

对B区域(第n层)单元中心配点得到全场声压pB为

联立式(15)、式(16)解得：

逐层算法优势不仅在于可以减小矩阵规模，而且能减小数据检测规模。在MoM 中，声源外部散射方程组通常表示发射器从某一个方向上发射超声波所对应的方程组，一般情况下检测阵列点数H小于ROI 区域总单元数M×(N-1)+1，此时式为关于像函数o的欠定方程组，为使其可解，需从Φ个方向上发射超声波，得到Φ×H个散射方程，使[Φ×H]≥M×(N-1)+1，此时方程组虽然可解，但也极大地扩充了矩阵规模与检测规模；逐层算法则不需通过上述方案补全不充分的检测阵列数据，因一次仅计算一层单元，轻易满足H≥M。

3 仿真

为验证“逐层算法”是否能够正确重建流体介质内部声场分布，本文对8 种模型进行仿真，将“逐层算法”与MoM得到的计算结果进行对比。在仿真时，仿真软件采用MATLAB R2021a；计算机处理器为Intel(R) Core(TM) i7-10700 CPU@2.90 GHz，运行内存为16 GB。为得到更直观的结果，直接对比ROI区域的散射场分布。因逐层算法需获取检测面信息作为已知量用于求解，检测面上测点的散射场由MoM得到。

入射声压、ROI区域相关参数如表1所示。

表1 入射声压、ROI 区域相关参数Table 1 Relevant parameters of incident sound pressure and ROI area

表1 中所给ROI 区域单元划分基于极坐标系，第n层任意单元节点周向坐标为r=a-nl，n=1,2,3,···；第n层中第m个单元节点径向坐标为θ=2mπa/l,m=1,2,3,···；结合上述ROI区域划分方法及表1 给出的入射声压相关参数，任意场点处入射声压可表示为

式(18)中，r为场点的位置向量，θ为r与x轴正方向的夹角。

对上述8 种模型设置不同的介质分布进行仿真，绘制ROI区域散射声压云图，如图3所示。

图3 ROI 区域散射声压云图Fig.3 Scattered Sound Pressure Cloud Chart in ROI Area

相较于MoM 一次性求解全部单元的未知量，逐层算法的优势主要在于将求解域分层后逐次计算，进而可减小计算机内存消耗，并降低对计算机的算力要求。如表2 所示，以模型7、模型8 为例，给出了逐层算法计算一层占用内存与MoM 计算占用内存。

表2 MoM 与逐层算法求解一层时所形成矩阵规模与内存占用情况Table 2 Matrix size and memory occupation of moment method and layer by layer algorithm when solving one layer

在模型7 中，ROI 区域内包含2395 个单元，每层单元数有126个单元，共划分20层。当使用MoM求解时，一次需要计算的矩阵规模为2395×2395，即需存储及处理5,736,025个元素，生成并处理矩阵占用了577 MB 内存；而采用逐层算法求解时，求解域划分为20 层，除最内层包含一个圆形单元外，其余每层均仅包含126 个矩形单元，一次运算时形成的矩阵规模为126×126，仅需存储及处理15,876个元素，生成并处理矩阵仅占用20 MB 内存，相较于MoM 大幅度减小。同理，在模型8 中，使用MoM 求解，生成并处理矩阵占用了424 MB 内存；采用逐层算法求解，生成并处理矩阵仅占用17 MB内存。

需要说明的是，文中为了采用MoM 的计算结果作为对比，因而将模型的规模设置得较小。在实际应用中，求解域的尺寸和入射波的频率可能会比算例中大得多。例如，若求解域的半径为0.5 m，入射波频率为1 MHz，同样在一个波长λ内划分5 个单元，那么总共就需要划分1668 层，每层10,472 个单元。此时，若采用逐层算法，每一层的矩阵规模均为10,472×10,472，经计算发现，在不考虑系统及软件需消耗的基础内存情况下，内存占用已经达到8.15 GB；而若采用MoM，其生成矩阵的规模为17,456,824×17,456,824，远远超过逐层算法，按照逐层算法一层计算所占内存与层数相乘估计，需消耗运行内存8.15 GB×1668=13,586 GB，远超普通计算机算力限额。由此可见，所需求解问题的规模越大，逐层算法相对于MoM的优势就越明显。

4 结论

针对超声散射求解非均匀流体介质内部散射声场的问题，本文提出了一种计算方案——逐层算法，结合近场声全息理论与声散射理论，实现逐层对非均匀流体介质内部散射声场求解。在数值仿真上以MoM 计算结果为参考，仿真结果表明，本文提出的逐层算法可以有效地重建非均匀流体介质内部散射声场，且由于一次仅计算一层单元，大幅度减小了矩阵的运算规模。

虽然本文中“逐层算法”只给出了在非均匀流体介质内部散射声场重建问题上的应用，但当介质对比度未知时，通过在式(11)、式(13)之间反复迭代，即首先给出介质对比度的初始估计，将其带入式(13)中求得较近似的全场，再将求得的全场带入式(11)中求解像函数，如此反复迭代便可逼近每一层单元像函数的真值。因此使用“逐层算法”重建非均匀流体介质内部散射声场问题是超声层析成像的第一步，本文提出并验证了“逐层算法”的可行性，为“逐层算法”在超声层析成像中的应用奠定了基础。