奥氏体不锈钢焊缝中的声学仿真模型与全聚焦成像检测

姜柏涛 阎守国 张碧星

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

奥氏体不锈钢具有优良的抗腐蚀性、抗氧化性、低温韧性等特点，在石油化工、机械、核电等领域应用广泛。奥氏体不锈钢在焊接过程中，受焊接设备、材料、工艺等因素影响，易产生不同程度的焊接缺陷。为了确保工业结构的安全性，对奥氏体不锈钢焊缝进行缺陷检测是十分必要的。由于奥氏体不锈钢的导热性较差，焊接过程中在焊缝内部会形成沿温度梯度方向的柱状晶粒，其尺寸与超声波长相当，从而对声波产生强烈的散射和能量衰减效应，并且柱状晶粒的取向分布使得焊缝内部呈现明显的非均匀性和各向异性，造成声束传播时的扭曲和变形。目前基于均匀介质模型的超声成像方法在奥氏体不锈钢焊缝缺陷检测时存在定位精度和成像分辨率的不足，无法满足奥氏体不锈钢焊缝检测的实际要求。

为了提高超声检测应用于奥氏体不锈钢焊缝的检测精度，首先需要采用合适的物理模型描述焊缝的晶向分布，以描述焊缝内部声波的传播特性。基于对奥氏体不锈钢焊缝实际晶粒取向分布特征的研究，国内外学者建立了多种不同的焊缝模型。Silk[1]基于射线追踪方法建立了焊缝模型，将焊缝及周围介质划分为晶粒取向相近的区域；Ogilvy[2-3]建立了描述V 形焊缝晶向结构的函数模型，将焊缝作为晶粒方向连续的非均匀介质进行处理，并以此为基础开发了RAYTRAIM 工具，用于计算超声能量的传播路径；Moysan 等[4]开发了MINA模型，能够结合显微观察结果，运用晶体生长机理、电子背散射衍射(EBSD)、X 射线分析等多种技术对晶粒取向做出预测，而无需建立完整物理模型；Spies[5]通过高斯声束模型计算了非均匀各向异性介质中单个换能器产生的超声声场，通过多层均匀介质和界面反射/折射来模拟各向异性。

基于焊缝的物理模型，可以对焊缝中的声波动力学行为进行模拟计算，对焊缝中的声波传播及其与缺陷的相互作用关系进行研究。1995 年，Fellinger 等[6]将电磁学领域中的弹性动力学有限积分技术(Elastodynamic finite integration technique,EFIT)应用于无损检测领域，对二维各向同性和各向异性场景进行了讨论并给出了数值结果。Halkjær 等[7]结合Ogilvy 焊缝模型和EFIT 方法，将不同焊缝参数下的A 扫描数值模拟结果与实验数据进行了对比，从而确定最佳焊缝参数，并与真实焊缝的显微图像进行比较。Hannemann 等[8]基于简化的竖直晶向V 型焊缝模型，将EFIT 模拟和实际检测取得的B 扫描图像进行了对比，结果显示二者具有良好的一致性，且在实验成像中观察到了理论和模拟中预测到的耦合SV波。另一方面，可以采用射线追踪、高斯声束等半解析算法对波束的传播路径进行计算和预测。Zhao 等[9]通过射线追踪模拟，对各向异性堆焊层中的声传播路径进行了计算，并通过实验进行了验证。Nowers 等[10]将计算机领域的Dijkstra 算法和A*算法应用于焊缝声传播路径追踪，对算法的最佳参数和计算精度、计算时间进行了研究和比较。杨敬等[11]对不同晶粒取向的多层焊缝模型进行了仿真，并基于步进法进行了全聚焦方法(Total focusing method,TFM)成像模拟。Guo 等[12]结合Ogilvy 焊缝模型、等效点源高斯声束模型和Dijkstra 算法，对钢-奥氏体焊缝-钢三层结构的辐射声场进行了计算，实现了声波在焊缝中的偏转和聚焦。半解析算法的优势在于能够对任意介质中的声传播进行追踪，因此尤其适用于复杂的各向异性介质场景，且能够对各种检查要求(例如不同的换能器类型)进行建模，快速计算出声波的传播路径。

本文基于Ogilvy 模型，建立非均匀各向异性焊缝的物理模型，通过Dijkstra 路径搜索算法，对该模型下的声波特性进行数值模拟和分析，预测声波在焊缝中的传播路径和传播时间，在此基础上结合TFM 成像方法对焊缝缺陷进行成像检测实验。本文的方法能够修正基于均匀介质模型的焊缝缺陷定位精度和成像分辨率问题，为奥氏体不锈钢钢焊缝成像检测提供一种新的可行方法。

1 基本理论

1.1 Ogilvy焊缝模型

Ogilvy 通过对V 型焊缝宏观金相图的研究，得出焊缝晶向分布的以下特征：

(1) 沿焊缝中心的长晶粒轴接近垂直；

(2) 对于两个倾斜边界平面处于相等且相反角度的焊缝，在穿过焊缝中心的“垂直”平面中存在近似反射对称性；

(3) 晶粒轴线斜率随着距焊缝中心距离的增加而减小；

(4) 沿焊接边缘倾斜面的晶粒轴斜率整个表面上近似恒定；

(5) 晶粒轴方向的变化率随着距焊接中心距离的增加而减小。

综合以上特征，Ogilvy[2]提出了近似描述V 型焊缝(图1)内各点晶粒取向的分布函数：

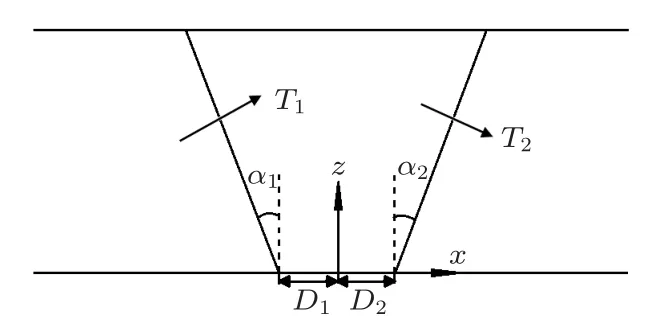
图1 V 型焊缝示意图Fig.1 The V-shaped weld

其中，θ表示焊缝区域内各点(x,z)处晶粒取向与x方向的夹角；D1和D2为焊缝底部原点到倾斜边界面的距离；α1和α2为焊缝坡口与z轴的夹角；η表示晶粒取向在x方向上变化的快慢程度；T1和T2与晶轴取向在左右两边界面(坡口面)上的斜率成正比。对于形状和参数确定的焊缝，通过式(1) 可给出焊缝区域内每一点处的晶粒取向。

1.2 各向异性介质中声速的计算

对于各向异性介质，由声波方程和简谐波解可得到Christopher方程：

其中，Γik=Cijklnjnl为Christopher 声张量，Cijkl为弹性张量，uk为k方向偏振位移，ρ为密度，c为波速，δil为Kroneckerδ函数，

若式(2)有非平凡解，则系数矩阵行列式必须为0，则有

即

对于某个特定的波矢方向n=(n1,n2,n3)，将其代入式(5)，求解得到特征值λi和特征向量vi：

其中，i=1,2,3，mi=ki/ω为慢度m的分量，pi为极化矢量的分量。相速度和群速度的分量可分别表示为

其中，i=1,2,3。

根据Ogilvy焊缝模型，可以得到焊缝区域内每一点的晶粒取向与x方向的夹角θ。将弹性常数变换到晶轴坐标系中，即可计算出各点处的相速度和群速度。群速度代表了能量的传播，根据Fermat能量最小作用原理，能量总是沿着时间最小的路径传播。当群速度分布被确定，就可以使用路径追踪方法确定基于群速度分布的时间最短路径，也就是声能量的传播路径。

1.3 Dijkstra路径搜索算法

通过射线追踪方法对声传播路径以及传播时间进行预测，能够得到更加接近于实际的聚焦延时，从而得到相对准确的成像结果。出于对成像实时性和准确性的要求，射线追踪算法需要具有尽可能高的计算效率。Dijkstra 算法是计算机领域常用的路径搜索算法之一，由荷兰科学家Dijkstra 在1959 年提出，用于解决有权图中两节点间的最短路径问题。Dijkstra 算法围绕两个列表进行，两个列表分别存放已知最短路径的节点和剩余所有节点，每个节点记录和更新自身与选定起点的最短路径长度值。算法的每一步以剩余节点列表中拥有最短路径的节点为操作对象，进行松弛操作——即比较路径长度，寻找并更新可能的更短路径长度。在每一步操作之后，都有一个节点由剩余节点列表移入已知最短路径节点列表，直至剩余节点列表为空，即所有节点到源点的最短路径均得到确定。

算法的具体操作如下[13]：

(1) 起始时，全部节点位于剩余节点列表(列表II)。选取一个节点作为起点，将其移入已知最短路径的节点列表(列表I)，其最短路径长度值为0。此时，列表II中节点的最短路径长度值均为无穷大，表示其到起点的最短路径未知。

(2) 找到与起点直接相连的节点，更新这些节点的最短路径长度值，其值为与起点之间的距离。

(3) 将列表II 中具有最小路径长度值的节点(下文称节点A)移入列表I。

(4) 考察与节点A直接相连，且仍在列表II 中的节点。若这些节点与节点A的距离加上节点A最短路径长度值的和小于这些节点中已记录的最短路径长度值，则更新这个最短路径长度，否则不做改变。

(5) 重复步骤(3)、步骤(4)，直至列表II 为空。此时所有节点中记录了到起点的最短路径长度值。

1.4 各向异性介质中的TFM成像方法

根据TFM 成像原理，成像点(x,z)的幅值计算式为

其中，tij为发射-接收对i-j对应场点(x,z)的传播时间。对于各向同性介质，声沿直线传播，有

其中，xi和xj分别为发射和接收阵元的横轴坐标。

对于各向异性介质，不同位置的声速并不相同，声传播路径并非直线，直接使用式(11)来计算声传播时间确定每个成像点的聚焦延时，所得到的结果是不准确的。对于确定晶粒取向分布的计算区域，将区域进行离散化，使用Bond 矩阵变换将弹性常数变换到晶轴坐标系中，由2.2 节，可计算出各离散点的群速度分布。基于路径搜索算法，计算换能器阵元的各个发射-接收对到各离散点的传播路径，结合群速度分布，即可求得传播时间τij(x,z)(i,j=1,2,···,n，n为换能器阵元数)。用τij替换各向同性介质中的传播时间tij，即可得到各向异性介质中TFM幅值的计算式：

2 数值仿真

2.1 焊缝仿真模型建立

按照如图2 所示的试块模型设置相关参数，建立焊缝仿真模型，计算焊缝晶粒取向分布。空间内各介质均为奥氏体钢(304 钢)，纵波声速5640 m/s，焊缝顶部长19.63 mm，底部长2 mm，焊缝两侧界面与底面夹角均为80°。焊缝区域内中心线上15 mm、25 mm、35 mm处分别有3个圆形通孔缺陷，直径为2 mm。图3 为根据仿真模型所生成的晶粒取向分布，其中的线条代表着焊缝内的柱状晶。可以看到采用Ogilvy 模型很好地模拟了堆焊条件下的焊缝内部结构特点。

图2 试块模型示意图Fig.2 The test block model

图3 焊缝仿真模型Fig.3 Simulation model of weld

2.2 声传播路径和传播时间计算

基于Ogilvy焊缝模型，可以计算得到焊缝区域内每一点的晶粒取向与x方向的夹角θ。在实际进行计算时，首先在需要计算的成像区域内分布大量节点，根据式(8)和式(9)计算出各节点处的相速度和群速度分布。

相邻两节点的传播时间t可表示为

其中，d为两节点距离，vg为两点间的群速度平均值。由于计算时相邻节点间距一般比较小，可以使用两端节点处的群速度值代替平均值vg。算法运行完成后，得到区域内所有节点到指定起点的最短传播时间。对每一个节点，通过逐级追踪父节点的方式可以得到源点到节点的传播路径。

图4 为位于(-20 mm,50 mm)处的点声源从一侧介质穿过焊缝区域，到达另一侧介质的传播路径计算结果。可以看到，在进入焊缝区域前，介质为各向同性，声传播路径为直线；进入各向异性焊缝区域后，声线发生扭曲和弯折，靠近焊缝中间区域弯折最为明显；穿过焊缝区域后，恢复直线传播。

图4 声传播路径计算结果Fig.4 Calculation result of sound propagation path

设置和计算节点分布时，需要考虑节点分布密度等相关参数的选取。如节点分布过密，则会显著影响计算速度；如节点分布过疏，则无法得到准确的计算结果。为方便比较，分别选取两组平均节点间距d：取d=2 mm、d=1 mm、d=0.5 mm 和d=0.2 mm、d=0.1 mm、d=0.05 mm，计算焊缝试块上表面(-20 mm,50 mm)穿过焊缝区域到达试块另一侧下表面(10 mm,0)(25 mm,0) (40 mm,0)三个终点的声传播路径，计算结果如图5所示。可以看到前一组设置的平均节点间距较大，导致计算精度不足，计算得到的声传播路径具有较大的差异；后一组设置的平均节点间距较小，所得到的声传播路径基本重合，表示计算精度已满足要求。结合计算资源情况，本文使用平均节点间距d=0.2 mm对声传播路径进行计算。

图5 不同节点平均间距d 下的声传播路径Fig.5 Sound propagation path under different node average spacing d

另外一个影响声传播路径计算结果的因素是路径搜索算法中的最大步进距离。以选定节点为圆心，最大步进距离为半径，范围内的所有节点即看作与选定节点直接相连。最大步进距离影响了算法每一步中需要计算、比较和更新的节点数量，进而同样影响计算效率。以节点平均间距d=0.2 mm为单位，选取n=2d、n=5d、n=8d和n=15d，计算与图5同样的声传播路径，结果如图6所示。可以看出，n=2d时的计算结果与其他路径差异较大，表明最大步进距离过小，每一步计算中未能考虑足够的相邻节点，导致计算出现偏差。n=5d、n=8d和n=15d时的计算路径大致重合，表明此时最大步进距离已满足精度要求。综合以上结果，采用d=0.2 mm，n=5d对声传播路径进行计算。

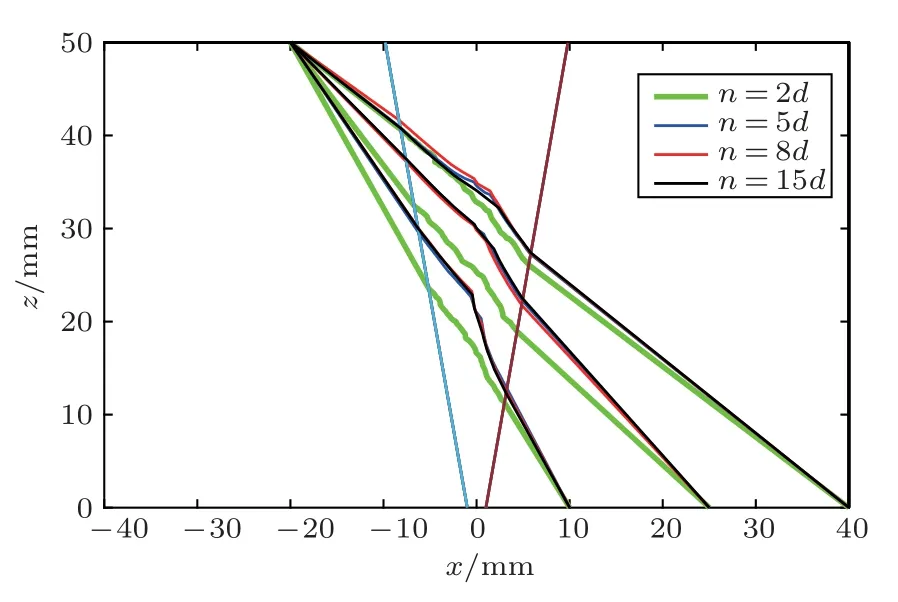
图6 不同最大步进距离n 的声传播路径Fig.6 Sound propagation path for different maximum step distance n

3 实验采集回波数据的修正

使用实验室超声相控阵系统(图7)进行实验检测并采集回波数据，焊缝试块(图8)的规格与图2相一致。

图7 实验室超声相控阵系统Fig.7 Ultrasonic phased array system

图8 焊缝试块实物图Fig.8 The weld test block

检测使用32 阵元探头，探头中心频率5 MHz，阵元宽度0.5 mm，阵元中心间距0.6 mm，使用单发全收模式，接收并存储基于全矩阵捕捉(Full matrix capture,FMC)的回波数据。基于实验设备的原始成像结果如图9 所示。为方便与下文修正后结果的比较，将图9 的原始成像结果使用计算机进行后处理，结果如图10 所示，缺陷的实际位置在图中由黑圈标出。

图9 原始成像结果Fig.9 The original imaging result

图10 处理后的原始成像结果Fig.10 The original imaging result after processing

选定计算范围为缺陷大致所在区域(-5 mm＜x ＜5 mm，10 mm＜z ＜40 mm)，按照平均节点间距d=0.2 mm、最大步进距离n=5d进行随机节点分布。基于Dijkstra 算法，首先计算以各阵元为起点、缺陷区域各离散点为终点的声传播时间，组合得到全部32阵元的各个发射-接收对到每个离散点的传播时间。根据各向异性下的TFM 成像原理(2.4 节)，使用计算得到的各发射-接收阵元对在各向异性情况下的传播时间，替换原始全矩阵回波数据的对应采样值，从而对成像结果进行修正，修正后的成像结果如图11所示，缺陷的实际位置在图中由黑圈标出。

图11 修正后的成像结果Fig.11 The corrected imaging result

对比图10和图11，(0,25 mm)和(0,35 mm)附近的缺陷分布范围和定位误差均减小，纵向中心和横向中心与仪器采集时记录的实际缺陷位置一致，修正效果较好。(0,15 mm)处缺陷的分辨率较低，无法看出明显的修正效果，可能与所在位置与声束主轴夹角过大、未能采集到清晰图像等因素有关。

4 结论

本文基于Ogilvy焊缝模型，建立了各向异性奥氏体不锈钢焊缝仿真模型，使用Dijkstra 路径搜索算法对各向异性焊缝中的声传播路径和传播时间进行了计算和理论分析。基于实验室超声相控阵系统，采集了焊缝试块的全矩阵回波数据。之后，根据各向异性下的TFM 成像原理，使用各向异性下的TFM 传播时间计算结果替换原始回波数据中的传播时间，从而对原始数据进行修正并重新成像。结果表明，这一方法能够有效修正基于均匀介质模型的传统TFM 成像所产生的缺陷定位精度和分辨率问题，为各向异性奥氏体不锈钢的超声检测提供了一种新的思路和方法。