横向各向同性地层快速各向异性反演方法*

2023-11-23宋云红赵妙颖

应用声学 2023年6期

关键词：通利横波插值

宋云红陈浩李超赵妙颖

(1 北华航天工业学院廊坊 065000)

(2 北京市海洋深部钻探测量工程技术研究中心北京 100190)

(3 中国科学院声学研究所北京 100190)

(4 中国科学院大学北京 100049)

0 引言

声波测井作为主要的石油测井方法之一，是探测地层各向异性的重要手段[1-4]。在横向各向同性(Vertical transversely isotropic,VTI)地层的声波测井中，往往只能测量得到地层垂直方向的纵波速度VP和横波速度VSV。Schoenberg 等[5]提出了一种简化的近似模型Annie 模型，随后Thomsen[6]进一步将VTI 介质的5 个独立弹性模量用3 个独立模量C33、C44和C66代替。Xu等[7]利用经典的5个模量表示的VTI模型测量的数据与采用3个模量的Annie 模型得到的数据对比，验证了Annie 模型的适用性。因此在测量获得地层密度、垂直方向纵横波速的基础上，只需得知水平方向横波速度就可近似表示VTI 地层。在对VTI 介质的研究中，很早人们就发现了斯通利波对VTI 地层尤其是慢地层中的剪切弹性模量C66灵敏度较高，也就是说斯通利波对VTI 地层的横观各向同性效应比较敏感[8-9]。因此人们通常利用斯通利波来反演VTI地层的水平横波速度VSH(对应弹性模量C66)，结合测井中测量的垂直横波速度VSV(对应弹性模量C44)，就可以得到垂直方向与水平方向的横波各向异性γ[6,10-11]。当地层横波速度较快时，斯通利波对横波各向异性的灵敏度下降，继续采用斯通利波反演VTI 地层各向异性时结果会存在较大误差[12]。为了更高精度地获得快速VTI 地层的各向异性大小，人们转而对VTI 介质中的偶极声场进行了进一步的研究。Sunaga 等[13]和Valero 等[14]发现VTI 介质中的偶极弯曲波频散在低频段受C44影响较大，然而在高频段对C66有较高的灵敏度。Fang 等[15]提出了利用宽频带的斯通利波和弯曲波来共同反演VTI地层的各向异性。Sinha等[16]提出利用一个等效的各向同性参考模型的弯曲波频散与测量弯曲波阵列波形的频散曲线在不同频段对其高灵敏度弹性模量进行反演，最终同时反演VTI 介质的5个模量，这种方法中参考模型的参数选定会对反演结果产生比较大的影响。Xu等[7]提出将C44和C66两个参数同时代入弯曲波频散计算中，与测量波形频散对比，同时反演出两个横波速度VSV和VSH以及各向异性大小γ。许松等[17]进一步提出利用斯通利波和弯曲波分频段比较对应的测量波形的频散，最终反演VTI 介质的各向异性，这种方法在快地层和慢地层中同样适用。

综合来看，VTI 地层中的各向异性反演基本都是采用将参数代入模式波理论频散计算，反复计算斯通利波或者弯曲波的理论频散曲线，来最佳匹配测量波形频散或者慢度。本文旨在对VTI 地层的模式波理论频散进行规律化研究，有效提高反演方法的效率，更加适用于大数据量的实际声波测井反演。

1 VTI地层理论频散分析

斯通利波是由井壁处固态-液态交界面的存在而产生的面波，主要在井中流体中传播，所以其对井中流体弹性参数(流体速度Vf和密度ρf)的灵敏度在全频段都保持比较高的水平。此外，前面提到斯通利波对TI 介质的横波相关模量(地层横波速度VSV、VSH和密度ρs)灵敏度较高，对地层其他弹性模量灵敏度较低[1]。垂直横波速度VSV在测井过程中可以测量得到，在计算斯通利波频散曲线时可以作为已知量，在这里不多做研究。因此首先主要研究斯通利波频散随Vf、ρf、VSH和ρs的变化规律。

首先研究慢地层中当VSV=1000 m/s 时，VSH在1000～1250 m/s 之间每隔10 m/s 变化，ρs在1900～2500 kg/m3之间每隔20 kg/m3变化，Vf在1400～1600 m/s 之间每隔10 m/s 变化，ρf在900～1300 kg/m3之间每隔10 kg/m3变化，跟随4个参数的变化计算参数变化后的斯通利波理论频散曲线。为了研究斯通利波理论频散曲线跟随每个参数变化的情况，下面采用控制变量法，对4个参数的变化影响逐个进行分析。

首先分析当Vf=1551 m/s、ρf=1000 kg/m3、ρs=2000 kg/m3时，VSH在1000～1250 m/s 之间每隔10 m/s 变化计算得到的斯通利波理论频散曲线，如图1 所示。可以看出，斯通利波理论频散曲线随VSH的增大而增大，其整体上看变化非常有规律性。

图1 斯通利波理论频散曲线随VSH 变化Fig.1 Variation of Stoneley wave theory dispersion curve with VSH

斯通利波理论频散曲线在ρs、Vf和ρf各自单独改变时的变化在图2 中给出。与斯通利波理论频散曲线随VSH的变化规律类似，参数变化时，斯通利波频散曲线形状整体而言变化比较规律。

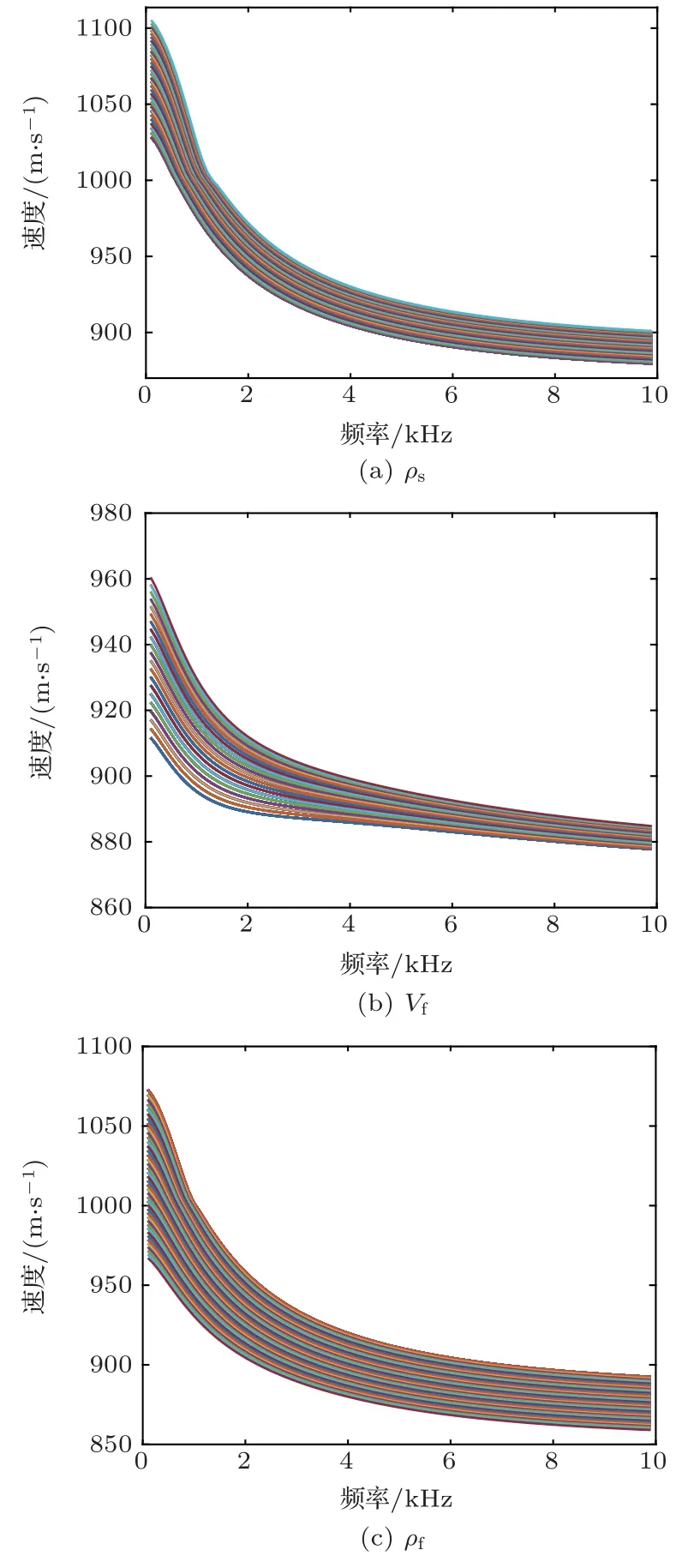
图2 斯通利波理论频散曲线随参数ρs、Vf、ρf 变化Fig.2 Variation of Stoneley wave theory dispersion curve with ρs, Vf, ρf

2 VTI地层频散曲线的插值计算

通过以上分析已知，VTI 地层斯通利波理论频散曲线随VSH、ρs、Vf和ρf变化非常具有规律性。本文提出利用插值法计算其理论频散曲线。首先采用两个横波速度VSH1和VSH2(VSH1＞VSH2)的理论频散曲线VSH1_t和VSH2_t来插值计算位于VSH1和VSH2之间的VSH3处频散曲线VSH3_i，并对VSH3的理论频散曲线VSH3_t与插值频散曲线VSH3_i进行误差分析。这里利用线性插值的方法，对每一个频率点f处，有

当VSH3位于二者中间位置时，VSH1_t和VSH2_t前面的系数相同，均为0.5，下文称为对称插值；当VSH3位于其他位置时，VSH1_t和VSH2_t前面的系数不同，下文称为非对称插值。首先利用1140 m/s 和1160 m/s、1090 m/s 和1210 m/s 以及1050 m/s和1250 m/s三组VSH1_t和VSH2_t来对称插值1150 m/s处的频散曲线，插值结果如图3(a)所示，可以看出3 组横波速度的插值频散曲线与理论频散曲线都非常接近，利用误差计算公式计算理论频散与插值频散之间的整体误差和最大误差分别为

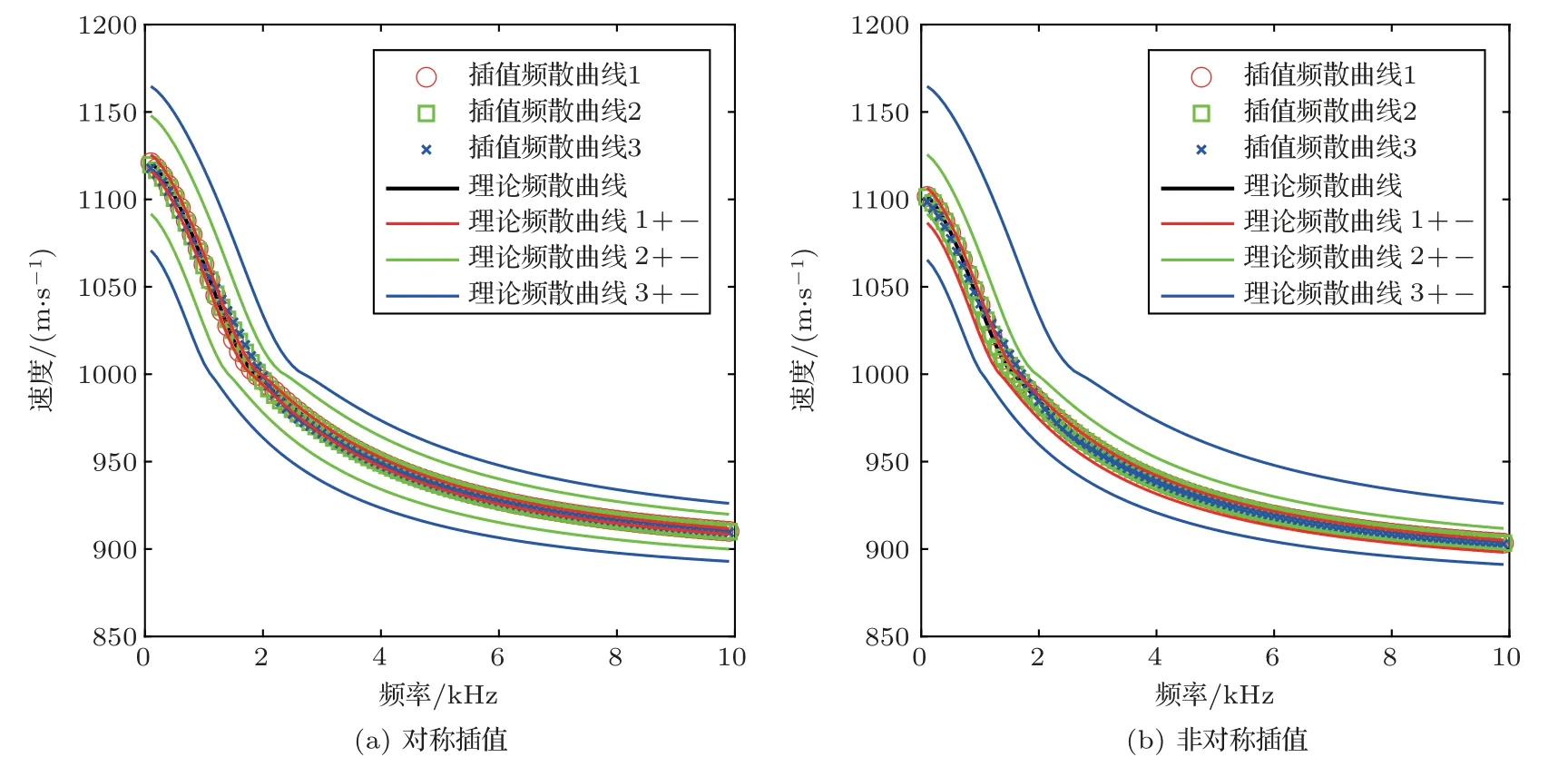
图3 斯通利波理论频散与VSH 插值频散曲线Fig.3 Theory dispersion and interpolation curve of different VSH of Stoneley wave

根据计算，3 组横波速度的对称插值的整体误差分别为0.00%、0.08%和0.20%，最大误差分别为0.04%、0.60%和1.04% (误差精确到0.01%，因此小于0.005%的记为0.00%)，误差都非常小，在可接受范围。

当需要计算频散曲线的VSH3不位于已知理论频散的两个横波速度的中间位置时，需要采用非对称插值方式。下面利用1080 m/s 和1120 m/s、1090 m/s和1160 m/s以及1040 m/s和1250 m/s 三组VSH1_t和VSH2_t来非对称插值1110 m/s 处的频散曲线，插值结果如图3(b)所示，可以看出3组横波速度的插值频散曲线与理论频散曲线都非常接近，利用误差计算公式计算理论频散与非插值频散之间的整体误差分别为0.01%、0.02%和0.17%，最大误差分别为0.09%、0.25%和0.94%，误差非常小，在误差允许范围。通过上面的误差分析，可以看出其他参数保持不变时，无论采用对称插值还是非对称插值方法，水平横波速度每隔200 m/s 计算一次理论频散曲线，就可以高精度地插值出位于其中不同速度的频散曲线。

对ρs、Vf和ρf分别为唯一变量的频散曲线采用对称插值和非对称插值方式，计算得到的插值频散曲线与理论频散曲线的对比情况在图4 中给出。图4 可以直观地体现出插值频散曲线与理论频散曲线一致性很好，具体的误差计算结果在表1 中给出。可以看出利用这3 个参数对斯通利波理论频散曲线插值计算的最大误差的最大值为1.63%，在误差允许范围。

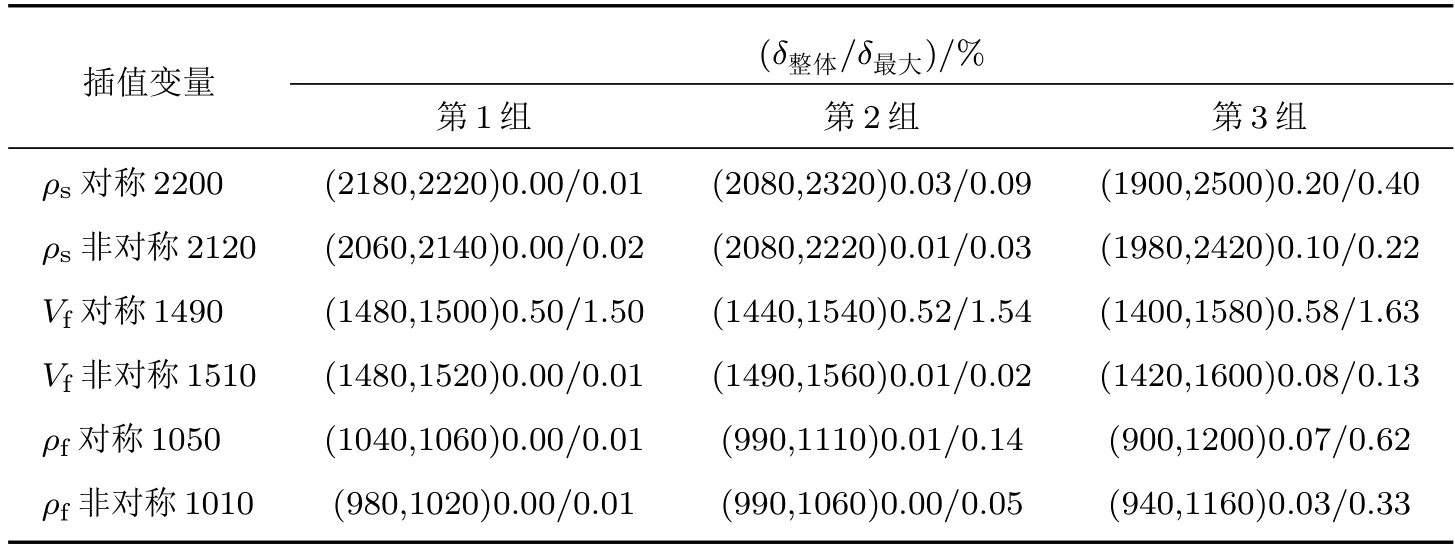
表1 斯通利波理论频散与对应ρs、Vf 和ρf 插值频散曲线的误差分析Table 1 Error analysis of theory and interpolation dispersion of Stoneley wave

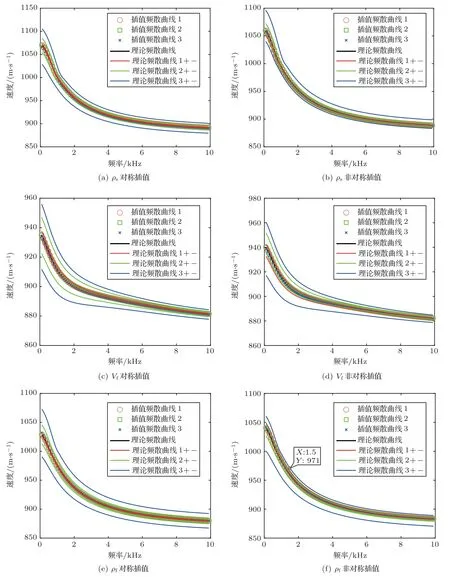
图4 斯通利波理论频散与插值频散曲线Fig.4 Theory dispersion and interpolation dispersion curve

上面计算的都是其他参数保持不变时，只对一个参数插值分析理论频散曲线和插值频散曲线的误差，下面观察多参数插值的结果。经过上面的分析，已知慢地层中斯通利波理论频散曲线对水平横波速度VSH和流体速度Vf的灵敏度较高，所以对这两个参数进行插值。假设需要的是参数为ρf=1000 kg/m3、ρs=2000 kg/m3、Vf=1551 m/s、VSH=1150 m/s 的地层斯通利波理论频散曲线，已知的是在ρf=1000 kg/m3、ρs=2000 kg/m3时，流体速度和水平横波速度分别为Vf=1400 m/s、VSH=1050 m/s；Vf=1600 m/s、VSH=1050 m/s；Vf=1400 m/s、VSH=1250 m/s和Vf=1600 m/s、VSH=1250 m/s 四种地层的斯通利波理论频散曲线。那么首先对Vf两两非对称插值，得到Vf=1551 m/s、VSH=1050 m/s和Vf=1551 m/s、VSH=1250 m/s，再将插值结果对VSH对称插值，最终得到需要的Vf=1551 m/s、VSH=1150 m/s 地层的斯通利波频散曲线。图5给出两次插值得到的频散曲线与直接计算的理论频散曲线，图5 中用VSH0表示1150 m/s，分别表示1250 m/s和1050 m/s，Vf0表示1551 m/s，分别表示1600 m/s 和1400 m/s。经分析，VSH0Vf0处的理论频散与两参数插值频散整体误差为0.24%，最大误差为0.96%，误差较小，在误差接受范围，也就是说对水平横波速度VSH和流体速度Vf各自在200 m/s 的步长范围内取值并进行两参数插值得到的插值频散曲线与理论频散曲线仍非常接近，在反演过程中可以用插值计算代替理论频散曲线的计算，将提高VTI 各向异性反演的效率，这一方法将在下面快速VTI 各向异性反演方法研究中进一步研究和探讨。

图5 斯通利波理论频散与VSH-Vf 两参数插值频散曲线Fig.5 Theory dispersion and interpolation dispersion curve of two parameters VSH-Vf

3 VTI地层各向异性快速反演方法

在对垂直横观各向同性地层进行反演方法研究前，首先对其进行正演模拟，得到VTI 地层的阵列波形数据，用于后续的反演方法研究。由于VTI地层中地层对称轴与井轴重合，具有解析性，可以利用实轴积分法计算单极子声源得到的波形数据。井中激发声源的频率响应谱为

其中，S(ω)是声源频谱，A(k,ω)是井对声源的频率-波数响应函数。将频率响应谱沿k平面的实轴积分，叠加源辐射的直达波，就可以得到声场函数：

其中，D(0)(ω)是单极子声源辐射对波形的贡献[1]。根据式(4)就可以计算得出单极子声源在井中激发的波形数据。

3.1 传统VTI各向异性反演方法

在VTI 地层中，尤其是慢速VTI 地层，斯通利波对其TI 效应，也就是弹性参数C66灵敏度较高，所以人们希望利用斯通利波来反演VTI 地层的各向异性参数。利用斯通利波反演VTI地层各向异性利用了频谱加权平均慢度定理[18]：

在快地层中，斯通利波对TI 效应灵敏度下降，用其反演VTI各向异性的可靠性受到影响。人们通过研究快地层中横波各向异性对弯曲波频散特性的作用，提出了利用宽频带偶极测井数据频散曲线与弯曲波理论频散曲线对比来反演C66[7]：

式(7)中，Sm和Sd分别为计算得到的弯曲波理论频散曲线和波形处理得到的频散曲线，SSV为垂直横波慢度。式(7)对垂直横波慢度和各向异性大小γ同时进行反演，为使目标函数对两个参数都保持较高的灵敏度，波形数据的频带应包含高频段、中频段和低频段。

由于慢地层中采用了斯通利波波形平均慢度，在进行波形慢度反演时，通常需要确定波形处理时间窗口，如果确定的时间窗口不太合适，可能会导致计算的平均慢度较大程度地偏离斯通利波时差。而且需要用到理论频散曲线与波形频谱相乘后积分，计算较为繁琐。基于上面提到的慢地层和快地层中两种不同的反演VTI 地层各向异性的γ的方法，在慢地层中同样利用理论频散曲线与波形频散直接比较来反演VTI 地层各向异性，给出与式(7)类似的反演目标函数：

这里假设垂直横波慢度已知，只对γ进行反演。可以通过一维最优化算法寻找目标函数最小值，如黄金分割法获取最优解，对应反演得到地层各向异性参数。

3.2 快速VTI各向异性反演方法

前面提到了传统VTI 各向异性反演过程中需要反复计算不同VSH时的斯通利波理论频散曲线，与波形的频散曲线对比，最终确定地层的水平横波速度和各向异性大小。在实际测井数据处理中，数据量非常大，反复计算理论频散曲线十分耗时，因此通过一种快速的反演方法来近似确定VTI 地层的各向异性大小。前面发现利用已知的斯通利波理论频散曲线可以较高精度地插值计算出不同参数大小的频散曲线。基于这种高精度的插值频散曲线，提出一种快速的VTI地层各向异性反演方法：

(1) 首先对流体速度Vf和地层水平横波速度VSH两参数大间隔取值，建立理论频散表，本文针对慢地层，ρf=1000 kg/m3，ρs=2000 kg/m3，Vf取1400 m/s 和1600 m/s 两个数值，VSH取1000 m/s、1200 m/s 和1400 m/s三个数值，共计算6 种组合参数下的理论频散曲线，保存在理论频散表ST中；

(2) 通过钻井泥浆参数得到测量井孔的流体速度Vf0[1]，ST 中的6 组理论频散数据针对Vf两两线型插值，得到3个VSH下Vf=Vf0的插值频散；

(3) 计算测量波形的频散，与3组插值频散逐个比较，当其处于两个频散中间区域时，得到VSH0的区间范围；

(4) 对VSH0的区间的两端和进行高密度插值，如在200 m/s 的间隔内每隔1 m/s 计算一次插值频散，比较波形频散与插值频散，两者最接近时得到VSH0≈，根据V′SH0 与地层垂直横波速度VSV可以计算得到VTI地层各向异性大小。

经过以上4 个步骤，就可以快速反演出VTI 地层的各向异性大小。

3.3 VTI地层各向异性反演结果分析

下面以ρf=1000 kg/m3、ρs=2000 kg/m3、Vs=1000 m/s、Vf=1551 m/s、VSH=1150 m/s的VTI 模型为例，根据Thomsen 定义的各向异性参数，可以得出该模型的各向异性γ=16.125%。这里假设其他参数已知，需要反演VSH的值。首先利用传统的波形频散与理论频散反复对比的方法进行反演，反演结果如图6 所示，反演得到的γ=15.8321%，误差δ=1.82%。根据反演参数计算的理论频散与波形频散一致性较好。在计算中进行了16步寻找最优解的过程，在个人计算机上耗时118.12 s。

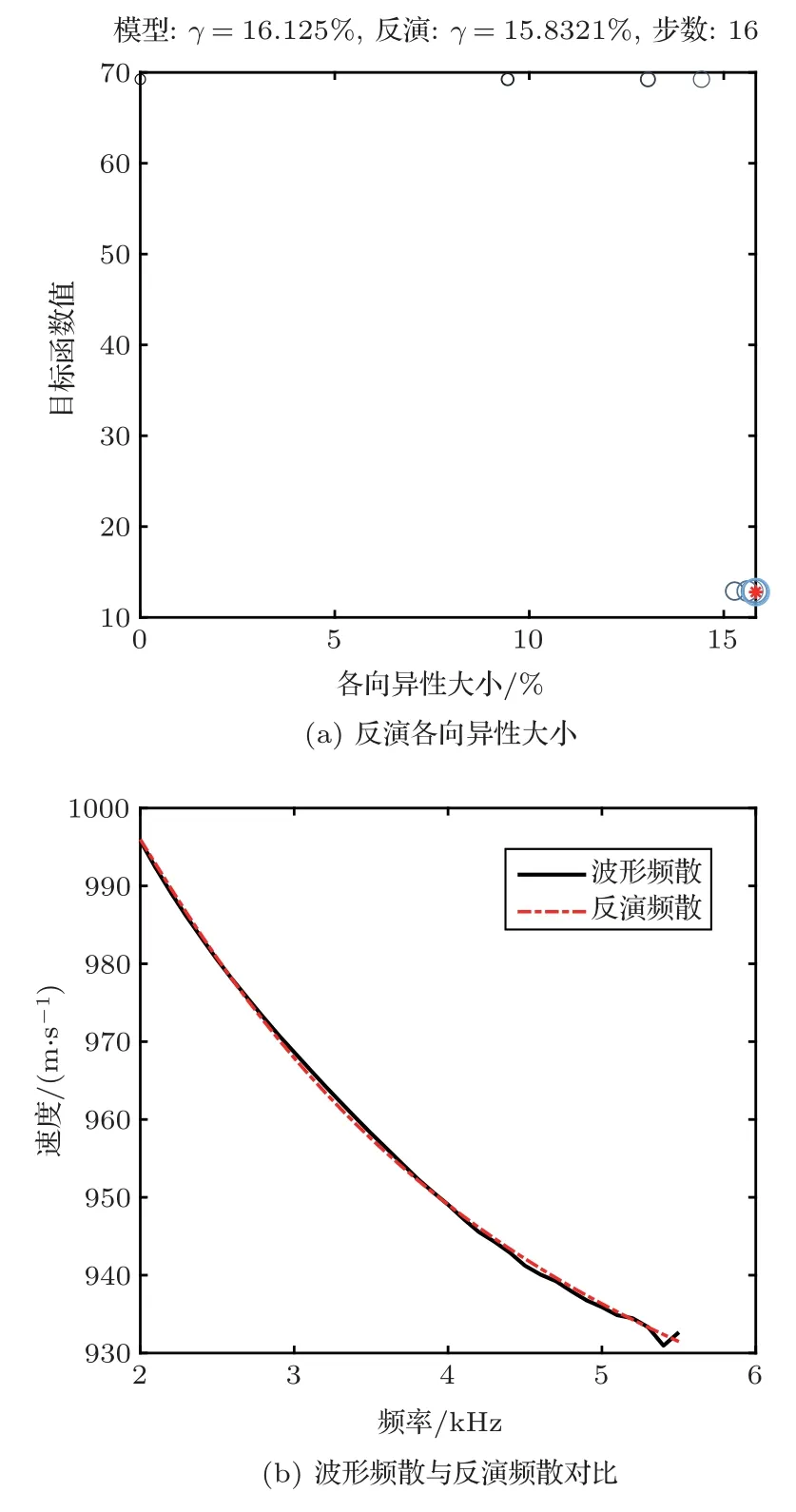
图6 传统VTI 各向异性反演结果Fig.6 Traditional VTI anisotropy inversion result

通过本文提出的利用频散插值快速反演VTI各向异性的方法进行反演，反演结果如图7 所示，反演得到的γ=16.7013%、δ=3.57%，相较传统反演方法误差略大，但仍在误差允许范围。与传统反演方法计算时使用同一台计算机设备，计算时间为0.78 s，相较于传统反演方法所需的118.12 s 大大缩减，在保证反演精度的同时大幅度地提高了VTI各向异性的反演效率，这一点对于处理大数据量的实际测井数据的商业软件来讲非常重要，为后续的测井解释商业软件设计与改进提供了理论基础与指导。

图7 两参数插值VTI 各向异性反演结果Fig.7 Two-parameter interpolation VTI anisotropy inversion result

利用商业软件处理实际测井资料时，除对于效率的要求外，由于现场测井的环境复杂，测量的数据包含很多因素导致的噪声，信噪比较低。为了检验该方法对于信噪比较低信号的可靠性，对数值模拟的数据人为添加噪声，这里添加了信噪比为0 dB 的高斯白噪声，添加噪声后的波形信号的第一列如图8(a)所示，可以看到噪声受到的干扰较严重。对加噪后的阵列波形数据利用本节提出的快速反演方法进行反演，结果如图8(b)所示，反演误差δ=5.00%，仍然比较可靠，证明该反演方法同时具备很好的抗噪性。