又逢比大小 方法知多少——对2023 四省测试第8 题的解析与拓展

福建省福清第三中学(350000)唐洵

1 题目与解析

由国家教育部教育考试院组织命制的2023 年四省(云南、吉林、黑龙江、安徽)高三数学适应性能力测试受到了业界的广泛关注,其中试卷的第8 题为比大小问题,其命题方式新颖独到,在注重知识的综合性与应用性考查的同时,又不失基础性.

题目(2023 年四省高三适应性能力测试第8 题) 已知a,b,c满足a=log5(2b+3b),c=log3(5b-2b),则( )

A.|a-c|≥|b-c|,|a-b|≥|b-c|

B.|a-c|≥|b-c|,|a-b|≤|b-c|

C.|a-c|≤|b-c|,|a-b|≥|b-c|

D.|a-c|≤|b-c|,|a-b|≤|b-c|

解法1(特殊值借力, 一步登天) 令b→0+, 则a→log52,c→-∞,易知|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

注当题设给出的a,b,c满足一定的等量关系或不等关系时,优先考虑选择满足条件的特殊值或者极限状态,通过运算分析排除若干错误选项;值得注意的是,特殊值要优选,例如本题中如令b=2,则a=log513,c=log321,在计算上就不如方法一来得简洁;但并非所有的比较大小问题都能够通过巧取特殊值来解决,下面再让我们来看看此类问题的一般性解法:

分析依题意, 5b-2b> 0, 即,则b> 0, 则a= log5(2b+3b) > log52 > 0; 注意到b= 1 时,a= 1,c= 1,此时|a-c| = |b-c| = |a-b| = 0.注意: 下面的解法均使用上述步骤,以下不再赘述.

解法2(差函数开路,披荆斩棘) ①若b>1,则

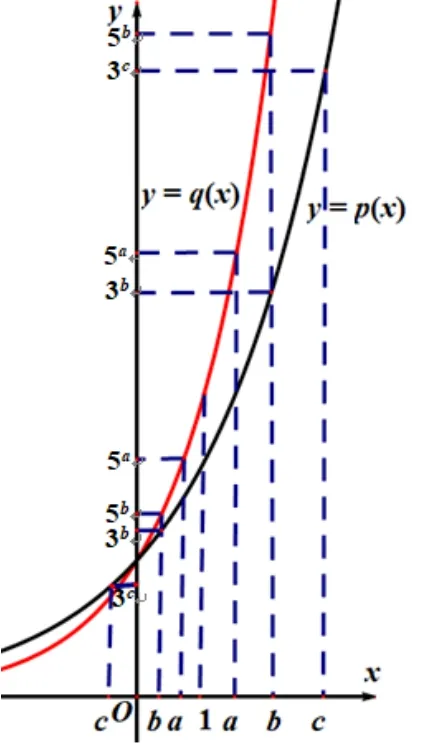
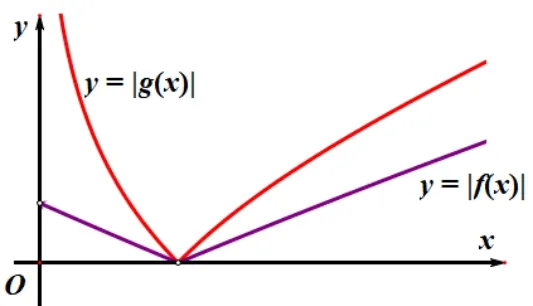
易知f(b) 在(1,+∞)上单调递减, 故f(b)

易知g(b) 在(1,+∞) 上单调递增, 故g(b) >g(1) = 0, 则c>b;故c>b>a>1,故|a-c|>|b-c|;

即a+c-2b>0,故0

②若0 a>b>c, 则|a-c| > |b-c|;a+c- 2b< 0, 则0

综上所述,|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

解法3(商函数摆渡,激流勇进) ①若b>1,易知a>1,c>1,则,故ab, 则c>b>a>1,故|a-c|>|b-c|;而

②若0 a>b>c,|a-c|>|b-c|;,|a-b|<|b-c|.

综上所述,|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

解法4(单调性协助,手到擒来)由a=log5(2b+3b)得,5a=2b+3b;由c=log3(5b-2b)得,3c=5b-2b.

①若b> 1, 易知51< 5a= 2b+ 3b< 5b,3c=5b-2b>3b,则c>b>a>1,故c-a>c-b>0,则|a-c|>|b-c|;而5a-3b=5b-3c=2b,且3b>3a>0,故, 则, 而, 故3b-a< 3c-b, 则0

②若0 a>b>c, 故a-c>b-c> 0, 则|a-c| > |b-c|;b-a>c-b,即a-b

综上所述,|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

方法五(图像法引航,乘风破浪)

令f(x)=log5(2x+3x),g(x)=log3(5x-2x),在同一直角坐标系中分别作出y=f(x),y=g(x),y=x在(0,+∞)上的大致图像如图1 所示;当0 1 时,结合图像易知|a-c| > |b-c|; 而5a= 2b+3b,3c= 5b-2b,则5a-5b= 3b-3c,令p(x) = 3x,q(x) = 5x,在同一直角坐标系中分别作出y=p(x),y=q(x)的大致图像如图2 所示;当0 1 时,结合指数函数高度与跨度之间的关系可知|b-c|>|a-b|.

图1

图2

综上所述,|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

解法5(导数法帮衬, 水滴石穿) 令f(b) =a-b=log5(2b+3b)-b,b∈(0,+∞),故

故f(b)在(0,+∞)上单调递减,而f(1)=0,故当0 0, 即1 >a>b; 当b> 1 时,f(b) < 0, 即b>a>1;令g(b)=b-c=b-log3(5b-2b),b∈(0,+∞),则

故g(b)在(0,+∞)上单调递减,而g(1)=0,故当0 0,即b>c,当b> 1 时,g(b) < 0,即c>b;故当0 a>b>c,当b> 1 时,c>b>a> 1,无论何种情况,都有|a-c|>|b-c|;而

其中

易知2 ln 3·ln 5-ln 2·ln 3-ln 2·ln 5>0,2 ln 3·ln 5-ln 2·ln 5-(ln 3)2>0,而

而0 >f′(b) >g′(b), 则 |f′(b)| <|g′(b)|, 而 |f(1)| =|g(1)| = 0, 结合上述单调性以及导函数的变化趋势,在同一直角坐标地中分别作出y=|f(x)|,y=|g(x)|的大致图像如图3 所示,观察可知,当b∈(0,1)∪(1,+∞)时,|f(b)|<|g(b)|,则|a-b|<|b-c|.

图3

综上所述,|a-c|≥|b-c|,|a-b|≤|b-c|,故选B.

注事实上,在比较a,b,c的大小关系时还可以使用对数平均不等式,过程如下,

由对数平均不等式可知,

故

若b>1,则

即a

则c>b>a>1;0

3 拓展延伸

基于上述问题,笔者通过联想得到如下推论:

推论1已知正数a,b,c满足1

证明依题意,令

综上所述,推论1 成立.

推论2已知正数a,b,c满足1

证明证法同推论1,从略.

推论3已知正数a,b,c满足1

证明若x=1,则|m-x|=|n-x|=|m-n|=0;若x>1,由推论1 可知,n>x>m>1,则|n-x|<|m-n|;而cm-bx=cx-bn=ax, 故,则, 故bx-m

综上所述,推论3 成立.

推论1-3 研究了a+b=c的情况,如果a+b̸=c,那么是否也有类似的推论呢? 笔者通过思考得到以下推论;

推论4已知正数a,b,c满足1c,则x0>1.

证明令当a+b 0,故∃x0∈(0,1),使得logc(ax0+bx0)=x0.而ax0+bx0=cx0,即bx0=cx0-ax0,故x0= logb(cx0-ax0); 同理可得,当a+b>c时,x0>1.综上所述,推论4 成立.

推论5m,n,x0的定义如推论4.若a,b,c∈(1,+∞),则∀x∈(x0,+∞),都有x0

推论6m,n,x0的定义如推论4.若a,b,c∈(1,+∞),则∀x∈(0,x0),都有n

推论5、6 的证法同推论1,此处从略.

推论7m,n,x0的定义如推论4.若a,b,c∈(1,+∞),则∀x∈(0,+∞),都有|m-x|≤|n-x|≤|m-n|,当且仅当x=x0时等号成立.

推论7 的证法同推论3,此处从略.

4 旧题新编

本题虽然作为单选题的压轴题,但由于四个选项的一致性,使用特值法可以轻松得到结论,这似乎命题意图的设定以及核心素养的考向相违背,鉴于此想法,笔者对题目稍作改编,得到如下试题,有兴趣的读者可以自行探究.

变式已知a,b,c满足a= log5(2b+2+ 3b),c=log3(5b-2b+2),现有如下说法: ①a>c; ②|a-c|≥|b-c|;③|a-b|≤|b-c|;则上述说法正确的数目为( )

A.0 B.1 C.2 D.3