考虑订单拆分的赛汝生产中多能工与任务分配协同优化
2023-11-22吴影辉曾少羽陈思思
吴影辉,曾少羽,陈思思
(江苏科技大学 经济管理学院,江苏 镇江 212100)
赛汝生产 (Seru production) 是源于日本电子工业生产现场的一种新生产模式,它能很好地适应多品种小批量的产品生产要求以及需求变动的市场环境[1]。这种生产方式在中国、韩国和其他国家也有应用。根据赛汝内的工人数量和工序任务划分,赛汝生产系统可分为分割式赛汝、巡回式赛汝和单人式赛汝类型[2-3]。与西方制造产业中装配单元不同的是,赛汝生产系统仅包含几个简单的设备和一个或多个能操作多个设备的工人 (即多能工),工人能独立完成一个产品的全部或大部分装配任务[4]。通过不同数量的赛汝单元以及多能工和工序任务分配组合,可构建不同类型的赛汝生产系统来提高生产效率和系统灵活性。
近年来,赛汝生产系统构建的相关问题得到国内外学者关注和研究。Yu 等[3]对赛汝生产系统设计优化问题进行了详细的综述。赛汝生产系统设计优化问题包含赛汝单元构建和批调度两个子问题。合理分配工人和工序任务以响应生产需求对提高赛汝系统的效率与柔性至关重要,因此多能工和任务分配是解决这两个子问题关键所在。Liu 等[4]研究流水线转换赛汝生产中赛汝单元构建个数和工人分配决策。随后,Yu 等[5]以总完工时间为目标,构建决策工人与任务分配的流水线转换赛汝生产优化模型。Ying 等[6]以最小化工人培训和产品加工时间成本为目标,研究工人-赛汝分配计划。然而这些研究忽略了工人本身固有的异质性,且在实际生产中将工人全部培训成全能工是不现实的。此外,这些研究的优化目标主要针对提高赛汝系统的生产效率,如总生产时间、总劳动时数、最大完工时间等,忽略了效率导向的工人和任务分配方案可能会导致工人间工作量不公平。作为一个“以人为本”的生产模式,公平地分配工作量不仅能增加工人对任务分配方案的接受度,而且能增强工人的公平感和满意度[7]。
随着对赛汝生产“以人为本”理念的重视,有学者开始关注赛汝单元间与工人间的工作量不平衡问题。Yu 等[8]以最大化全能工间、赛汝生产单元间的工作量平衡为决策目标,研究赛汝间与赛汝内工人工作量均衡问题。廉洁等[9]和Lian 等[10]研究赛汝系统多能工分配问题,构建一个双目标模型旨在实现赛汝单元间工人工作量均衡。Yilmaz[11]考虑赛汝系统中全能工可跨单元移动对总工期和工人间工作量的影响,研究全能工调度问题。Liu 等[12]研究混合赛汝系统中交叉培训工人分配问题以权衡生产效率和工人工作量均衡问题。王晔等[13]研究基于不同多能工技能水平组合下对工人间工作时间差异和总完工时间的影响。然而,以上研究均假设订单批次是不可拆分的。
订单拆分是指将同一批次的订单任务分配到不同赛汝中并行加工,是实现生产系统工作量平衡的重要方法[14]。其他生产系统的相关研究结果已证实,实行批量拆分可以降低库存成本和机器闲置成本、减少人员需求和工作时间,减少能源消耗等生产指标[15]。针对赛汝生产系统,现有研究大多不考虑订单拆分,假设一个批次订单只能在一个赛汝单元生产,仅有两篇文章在赛汝生产系统构建中考虑了订单拆分。白朝阳等[16]构建以最小化总完工时间和最小化工人总工时为目标的双目标模型,以实现赛汝生产单元构建和批量分割联合决策问题。
基于此,本文以平衡多能工间工作量为目标,研究考虑订单拆分的赛汝生产系统多能工与任务分配联合决策优化问题。以最小化工人最大工作量为优化目标函数,构建考虑订单拆分和公平性导向的混合整数非线性规划模型。为验证模型的有效性,还构建了考虑订单不拆分、订单拆分但优化系统效率指标的模型。这些模型被线性化后,采用优化软件CPLEX 求得精确解。算例实验表明,与不考虑订单拆分或系统效率导向模型相比,考虑订单拆分的公平性导向模型对工人工作量公平分配改善效果更优,同时能维持较高的生产效率。本文的研究丰富了赛汝生产理论,并为生产企业实施赛汝生产提供有价值的指导建议。
1 问题描述
1.1 符号定义与问题描述
为方便描述问题和建模,相关变量定义见表1。考虑一个由赛汝单元构成的生产系统,具有多名多能工。每个多能工可承担加工产品所需的单个或多个装配任务。现有若干批次产品需要完成生产,每个批次包含一种产品类型和相应的批量,每种产品的加工任务可由多个工人执行。考虑多能工所掌握的加工技能集和对每个工序加工任务的熟练程度具有异质性。如图1 所示,批次b1产品需要完成 工 序 任 务 集 为 {s1,s2,s3,s4,s5,s6,s7} 。 工 人w1能 够 承担的工序任务集为 {s1,s4,s5,s6,s7} 。不同多能工组合以及分配到相同赛汝的加工产品批次和批量将影响生产效率和每个多能工承担的工作量。每个赛汝单元的多能工加工技能集要能满足该赛汝单元内被分配加工产品所需的加工任务。本文考虑同批次产品被分配到不同的赛汝单元生产 (订单拆分),以最小化工人最大工作量为目标,如何将工人分配到不同的赛汝单元,以及确定分配到赛汝单元的各批次产品批量和工人承担被分配到同一赛汝单元内的各批次产品工序任务,从而完成生产任务。
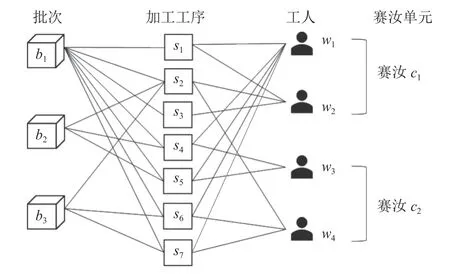
图1 一个简单的赛汝生产系统Figure 1 A simple Seru production system

表1 符号及其含义说明Table 1 Symbols and their meanings
1.2 基本假设
本文研究的问题基于以下假设。
1) 产品的类型和批次大小、每种产品类型的所有任务的标准加工时间都是预先知道的,并且每批包含一种产品类型。
2) 对于每个赛汝中的某个工序加工任务,只能由一个工人加工。工人只能被分配到他们能胜任的工序任务,不考虑工人培训。
3) 由于赛汝生产系统布局紧凑,工人在不同工作站之间的移动时间被忽略。
2 模型构建
基于上述符号定义和模型假设,考虑订单拆分的赛汝生产系统多能工与任务分配联合决策优化模型 (模型1) 如式 (1) ~ (16) 所示。
其中,目标函数 (1) 表示最小化工人最大工作量;约束 (2) 表示每个工人只能被分配到一个赛汝单元内;约束 (3) 限制每个赛汝单元内的总工人数量不超过最大值N;约束 (4) 表示每个批次被拆分并分配到赛汝单元的产品数量之和等于批次批量;约束 (5) 表示工人只能被分配给能胜任的工序任务;约束 (6) 表示每个工人承担每个批次产品工序任务总数不能超过该工人所能承受的最大任务数M;约束 (7) 表示每个批次b产品每个工序任务均有相对应的工人来完成;约束 (8) 表示批次加工工序只能被分配给同一赛汝单元的工人承担;约束 (9) 计算赛汝系统中每个工人的工作量;约束 (10) ~ (11) 表示决策变量Qbc的取值范围;约束 (12) 表示若批次b被分配到赛汝c中加工,即ybc= 1,Qbc的值至少为1,若Qbc=0 ,则ybc= 0;约束 (13) ~ (16) 表示决策变量xwc、ybc和的取值范围。
为验证模型1 的有效性,基于订单拆分与否和工作量公平性和系统效率优化目标组合,还构建了其他3 种模型。这些模型与模型1 的比较如表2 所示。
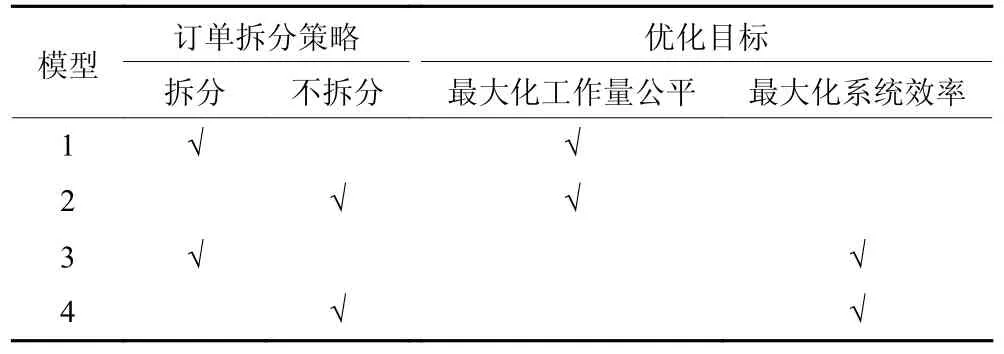
表2 基于不同订单拆分策略和优化目标的模型对比Table 2 Comparisons of models based on different lot-splitting strategies and optimization objectives
模型2 和模型4 不考虑订单拆分,需删除模型1 中的决策变量Qbc及约束 (4)、(10) ~ (12);每个批次的产品将全部在一个赛汝单元内生产,决策变量修改为,约束 (5) ~ (9)、约束 (13) 和约束 (16)将依次被修改为
此外,模型3 和模型4 的优化目标为最大化系统生产效率。在以往研究中,通常采用总加工时间(total labour hours, TLH) 来 衡 量 赛 汝 系 统 生 产 效率。因此,模型3 和模型4 的目标函数为
综上,模型2、模型3 和模型4 可分别表示如下。
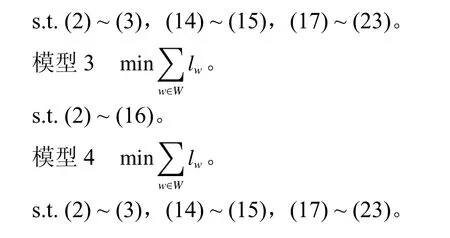
3 模型线性化处理
考虑到上述4 个模型中存在非线性部分,为了能采用优化求解器如CPLEX,获得这些问题的精确解,需要对这些模型中的非线性目标函数 (1) 和非线性约束 (8) ~ (9) 和 (20) 进行线性化处理[7,17]。
引入辅助变量 λ ,目标函数 (1) 可由式 (25) 和(26) 代替。
对于约束 (8),通过引入辅助连续变量uwbc∈[0,1] 代 替xwcybc并添加约束 (27) ~ (31) 将其线性化处理。对于约束 (20) 可做类似线性化处理。
4 算例与计算实验
采用Java 语言编写实验程序,调用优化求解器CPLEX 12.8 完成算例求解。所有数值实验在配备Intel Core i5-5200U 处理器、4GB DDR3 容量内存和Windows 10 操作系统的个人计算机上完成。如无特殊说明,下文模型1 ~ 4 均指线性化处理后的对应模型。
4.1 算例参数与示例
为验证模型1 的有效性,基于文献[11]中算例参数的取值范围 (如表3 所示),生成10 组算例进行求解。这些参数包括赛汝单元数量 |C| 、批次数量|B|、 工人数量 |W| 、 产品总工序数 |S| ,各批次批量Vb、工序标准加工时间tbs、工人对各工序的熟练程度fws。此外,针对所有算例,赛汝单元内工人数上限N设为4,工人承担同批产品最多工序数M为5。该算例包含4 个赛汝单元、10 名多能工、8 个订单批次,各批次产品工序及标准加工时间见表4,工人掌握的工序及其熟练程度见表5,各批次批量Vb见表6。

表3 算例参数取值范围Table 3 Ranges of instance parameters
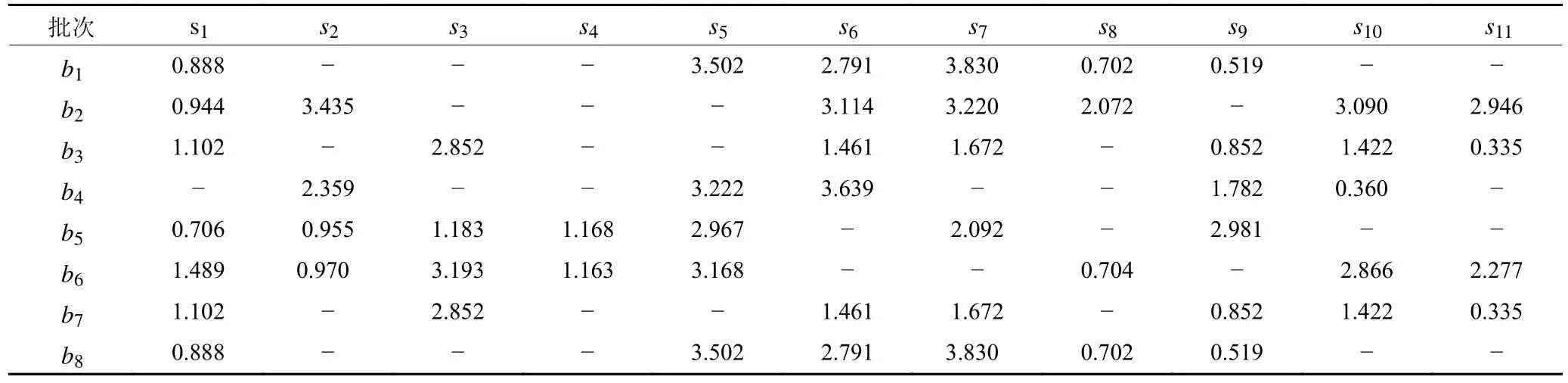
表4 各批产品工序的标准加工时间Table 4 Standard processing time of each task
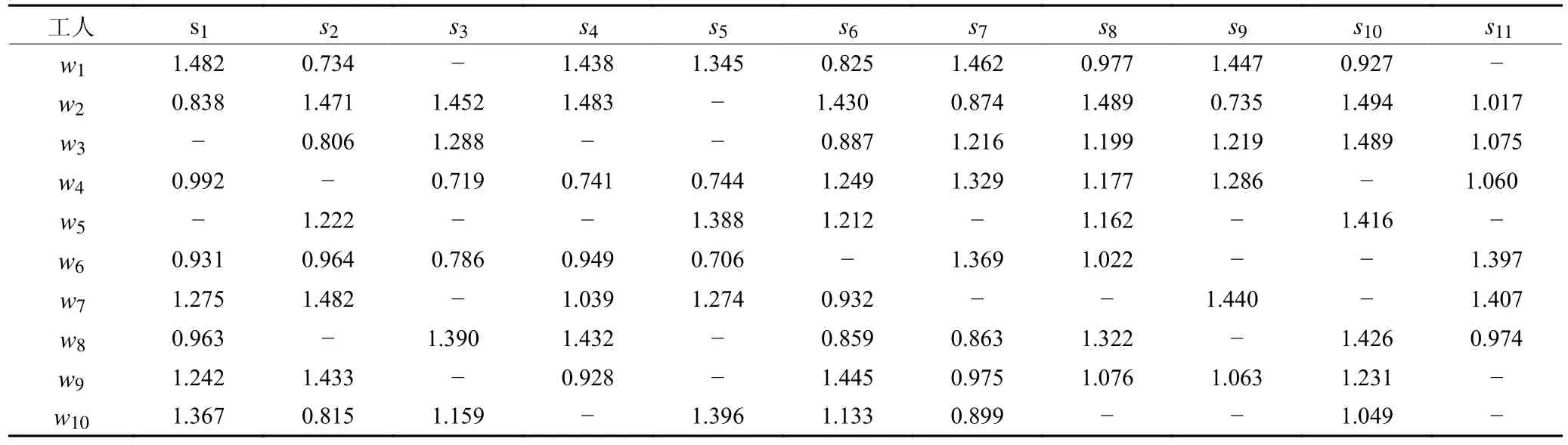
表5 工人掌握工序加工技能熟练程度Table 5 Workers' proficiency in operating skills

表6 订单产品数量信息Table 6 Product batch quantity
4.2 算例求解结果
由于篇幅所限,本部分仅给出示例算例在模型1 下的求解结果,如表7 ~ 9 所示。表7 为每个赛汝被分配的工人和加工批量情况。表7 中的数字表示各批产品分配到每个赛汝的批量Qbc,赛汝c1~c4被 依 次 分 配 的 工 人 为 {w4,w7,w10} 、 {w1,w8} 、 {w2,w5} 、{w3,w6,w9}。表8 表示每个工人承担的加工任务。表9 给出每个工人承担的工作量,可以看出工人间被分配的工作量较均衡,且最大差值只有0.7。

表7 工人与产品批量分配结果Table 7 Worker assignment and batch allocation results

表8 每个工人在赛汝单元内承担的加工任务Table 8 Operating tasks allocated to each worker in Serus

表9 每个工人被分配的工作量Table 9 The workload assigned to each worker
4.3 不同模型下求解结果对比分析
为了验证考虑订单拆分和模型1 的有效性,产生10 组算例进行数值实验分析。算例由主要参数 |B| 、 |C| 、 |W| 和 |S| 表示规模大小,如表10 所示。表11和表12 给出模型1 ~ 模型4 求解这10 组算例的 结 果。采 用 T LH 和 M WW 值来衡量模 型 的 有 效性, T LH 表示赛汝生产系统产品生产总时间,为系统生产效率指标; M WW 表示工人最大工作量,为缓解工人工作量 不均衡的优化目 标。 ΔTLH和 ΔMWW按式 (36) 和 (37) 计算。
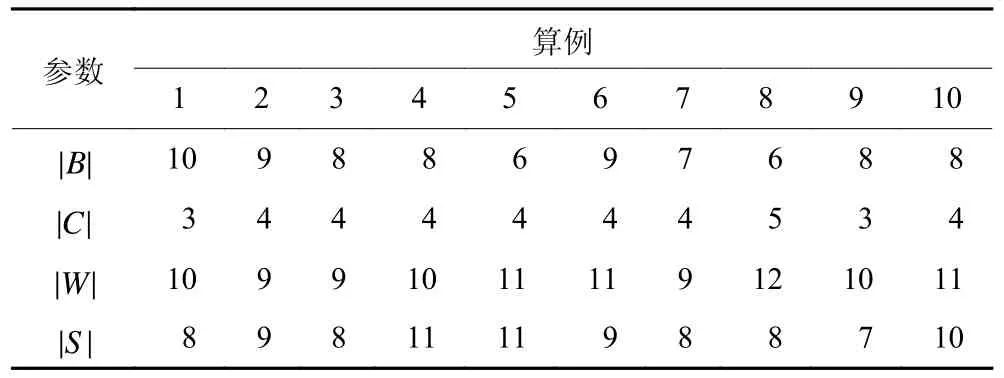
表10 实验算例及其参数值Table 10 Experimental instances and the values of parameters
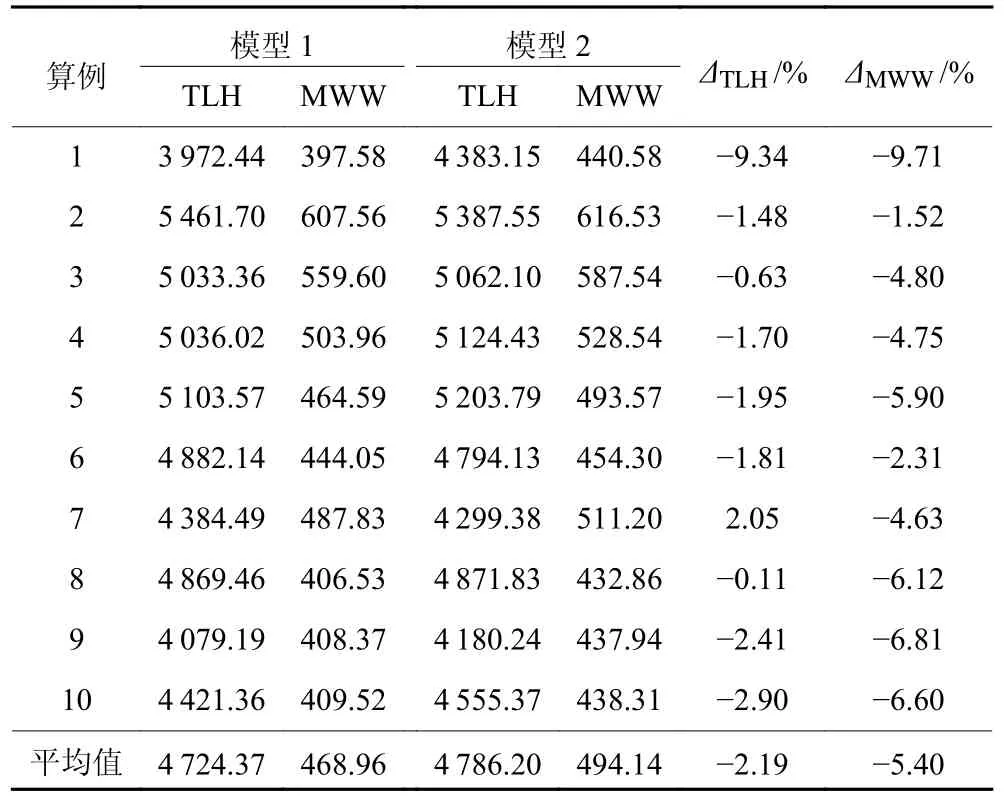
表11 以减少最大化工作量为目标的模型1 和模型2 求解结果对比分析Table 11 Comparisons of results obtained by models 1 and 2 with the objective of minimizing the maximum workload
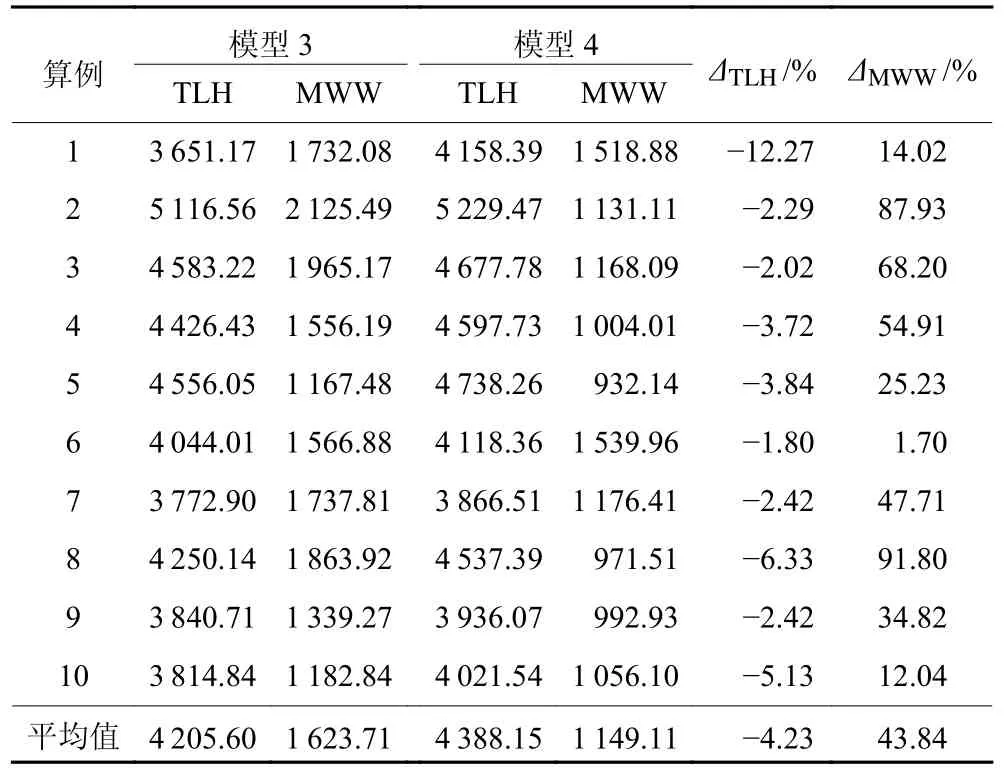
表12 以最大化系统效率为目标的模型3 和模型4求解结果对比分析Table 12 Comparisons of results obtained by models 3 and 4 with the objective of maximizing system efficiency
计算结果表明,相对于不考虑订单拆分的模型2,模型1 可最多减少工人最大工作量9.71%,平均减少5.40%;最大减少产品总加工时间9.34%,平均减少2.19%。这说明在公平性导向的模型中考虑订单拆分不仅能减少工人间工作量分配不均衡,还能提高系统生产效率。表12 表明,考虑订单拆分模型3 在提升赛汝系统生产效率指标上比模型4 更好,但造成工人间的工作量分配更加不公平。模型1 (或模型2) 与模型3 (或模型4) 比较的结果显示,公平性导向的模型能极大地改进工人间的工作量不均衡,仅稍微减少系统生产效率。综上,验证了本文构建的模型1 是有效的。
4.4 不同模型下工人工作量分布对比分析
图2 和图3 给出以算例5 和算例9 为例,求解模型1 ~ 模型4 的工人工作量分布情况。由图2 和图3 可知,相对于公平性导向的模型1 和模型2,系统生产效率导向模型3 和模型4 得到的工人的工作量分配极为不均衡。在以系统生产效率导向模型中考虑订单拆分并不能实现工人工作量均衡。尽管以公平性导向为目标的模型2 没有考虑订单拆分,但比模型3 和模型4 更能实现工人间工作量均衡。而考虑订单拆分且以公平性导向为目标的模型1 取得了最好的工人间工作量均衡。
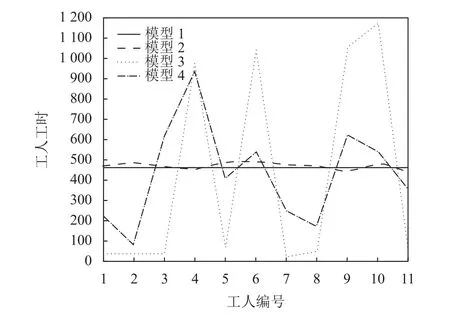
图2 针对算例5 不同模型下求得的工人工作量分布Figure 2 Workload distribution of workers obtained by different models for instance 5
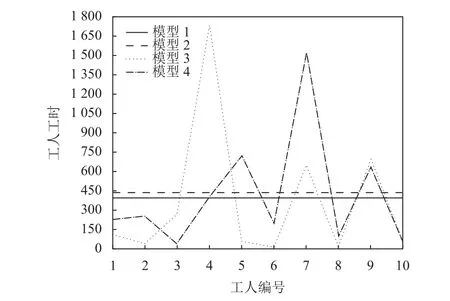
图3 针对算例9 不同模型下求得的工人工作量分布Figure 3 Workload distribution of workers obtained by different models for instance 9
5 结论
本文研究了考虑订单拆分赛汝生产系统中多能工与任务分配联合决策优化问题。为缓解赛汝生产系统中工人间工作量分配不公平,构建求解该问题的混合整数非线性规划模型,通过引入多个连续变量和约束,对该模型进行线性化处理。为验证模型的有效性,还基于订单拆分与否分别与工作量公平性和系统效率优化目标组合,构建3 个对照模型并采用优化软件CPLEX 求解问题。研究结论如下。
1) 算例实验表明,相对于不考虑订单拆分的模型2,本文提出的模型1 可最多减少工人最大工作量9.71%,平均减少5.40%;最大减少产品总加工时间9.34%,平均减少2.19%。这说明在公平性导向的模型中考虑订单拆分不仅能减少工人间工作量分配不均衡,还能提高系统生产效率。
2) 考虑订单拆分的模型3 在提升赛汝系统生产效率指标上比模型4 更好,但造成工人间的工作量分配更加不公平。生产总时间平均减少4.23%,但工人的最大工作量增加了43.84%。因此,在系统效率导向模型中考虑订单拆分可以一定程度上提高生产效率,但造成工人间极大的工作量不均衡。
本文研究的对象是纯赛汝生产系统,接下来可研究混合赛汝生产系统的异质工人分配和批调度问题。
