基于图神经网络的云制造服务推荐方法研究
2023-11-22董学文石宇强田永政
董学文,石宇强,田永政
(西南科技大学 制造科学与工程学院,四川 绵阳 621010)
在制造业呈现服务化转型发展的背景下,云制造作为一种新型制造模式,可以有效推进制造企业的服务化转型升级[1]。在云制造模式下,制造企业可以依据自身情况,将闲置的制造服务资源进行整合与封装,然后发布至云制造服务平台上。平台会对这些海量的、分散的制造资源进行管理或组合,并提供给有制造服务需求的企业用户,以达到制造资源的充分利用,从而提高企业的资源配置效率与企业竞争力[2-3]。
但是,伴随着制造业规模的不断扩大,云制造服务平台上海量的制造服务数据给制造服务的需求方带来严重的信息过载问题,增加了决策复杂度[4]。因此,针对制造服务推荐系统的研究得到了广泛关注。在各类互联网平台上,推荐系统是应对信息过载问题最常用的手段之一,其能主动地向制造服务需求方提供合适的制造服务资源[5],有助于缓解云制造服务系统出现的严重信息过载问题,从而提高云制造平台的服务效率。
目前,利用个性化推荐系统进行制造服务资源推荐的研究主要从用户偏好、资源组合推荐以及用户聚类等角度展开。禹春霞等[6]利用不同用户对制造服务各项指标的偏好来构建服务推荐模型,向用户推荐可能满意的服务资源。Zhang 等[7]利用客户的交易数据,获取用户与制造服务资源之间的交互关系,使用协同过滤算法实现对用户的制造服务推荐。Fan 等[5]利用聚类算法对有不同制造服务需求的用户进行聚类分析,以此进行制造服务资源的推荐研究。鲁城华等[8]在进行用户聚类分析的基础上,结合大数据技术,提出基于大数据分析与处理技术的制造服务推荐方法,获得较好的推荐效果。万年红等[9]从算法的敏捷性、智能性以及平稳性等角度提出一种多目标事务模糊关联聚类的云制造服务组合推荐算法,且具有一定的应用价值。然而,传统的推荐算法无法有效利用资源之间的隐藏特征,只能从用户与服务之间过去的交互中学习低维和线性特征,当数据规模增大时会带来较高的计算成本,从而导致不理想的推荐效果[10]。针对此问题,Simeone 等[11]将深度学习算法引入到制造服务的推荐过程中,以提升推荐的准确度与效率。
综上所述,现有研究从用户聚类或者基于用户的协同过滤推荐等角度出发,忽略云制造服务平台上制造服务资源之间的关联性与相似性。针对上述问题,本文构建基于制造服务供应商相似性的图数据集,在此基础上提出一种基于图神经网络算法的云制造服务推荐方法,并且取得了较好的链接预测效果。该方法有效克服了传统推荐算法无法利用数据高维特征的局限性,有利于提升云制造服务推荐系统的性能,提高用户的决策效率。
1 云制造服务资源图构建
1.1 特征与数据集
MFG.com 是最目前世界上具潜力的云制造公司之一,为了更真实地反映制造服务资源的特点,在该平台上采集了3 000 条制造服务资源信息。每一条制造服务数据的背后都是一个真实存在的制造企业,这些制造企业所提供的制造服务涵盖了铸造、3D 打印、装配以及注塑等30 余种类型。为反映制造服务资源的制造能力信息,将选取的3 000个制造服务供应商所涉及的34 种制造服务作为制造服务供应商的特征集合,故每个集合共包含34 个特征。每个制造服务供应商均对应一个特征集合,表示为Mn(n=1,2,3,···,3 000) ,制造服务供应商的特征表示为fi(i=1,2,3,···,34) 。因此,每个制造服务供应商表示为Mn={f1,f2,f3,···,f34} ,进一步将其表示为多维向量Mn=(f1,f2,f3,···,f34) 。
对于集合里的每一个特征,即每一种制造服务,如果制造服务供应商具备该特征,则令fi= 1,反之,则fi= 0。根据上述方法,得到一个规模为3 000×34 的二元特征矩阵Af。然后,以制造服务供应商的特征向量计算各个供应商之间的相似程度,并在此基础上构建对应的邻接矩阵,邻接矩阵存储着图的具体信息。在本文中,图表示为G(V,E),其中,V表示节点集合且V∈Rn×di;R表示集合所满足的关系;n代表节点的数量;di 表示特征的维度;E表示边的集合且E∈Rn×n。图中的节点表示制造服务供应商,边表示对应两个供应商之间的相似程度,且该图是一个无向图。
1.2 相似性度量
为研究资源之间相似性度量方法对图的结构信息的影响,本文采用欧几里得相似度、余弦相似度、皮尔逊相关系数以及杰卡德相关系数4 种常用的相似性度量方法进行计算。
欧几里得相似度衡量的是空间中任意两个点的真实距离,距离越小相似度越大[12]。余弦相似度是通过计算两个向量夹角的余弦值来判断向量的相似程度,值越接近于1,表明两个向量越相似[13]。皮尔逊相关系数等于向量之间的协方差与它们各自标准差的乘积的比值。计算所得的值趋近于0 时,则表示两个向量的相关性越弱;而值越接近1 或-1时,则表示两个向量具备较高的关联性[14]。杰卡德相关系数常被应用于计算两个集合的相关性,也可以用于度量两个二元多维向量的相似程度,通过计算两个向量中对应位置元素相同的个数占所有元素的比例来进行衡量[15]。4 种相似度的计算方法依次如下。
欧几里得相似度 (Euclidean) 为
余弦相似度 (Cosine) 为
皮尔逊相关系数 (Pearson) 为
杰卡德相关系数 (Jaccard) 为
其中,sim (a,b) 表示向量a与向量b的相似度或相关系数,在本文中,代表不同制造服务资源向量Mn之间的相似度。式 (4) 中,M11表示两个向量对应位置均是1 的维度个数;M01表示向量a中某个维度位置为0,同时向量b对应位置是1 的维度个数;M10则表示向量a中某个维度位置为1,同时向量b对应位置是0 的维度个数。在后续的研究中,为了便于进行统一度量,将4 种相似度计算方法所得到的具体数值进行归一化处理。
1.3 图的结构信息
将数据处理得到的制造服务供应商特征矩阵Af带入4 种相似度计算方法中,经数据归一化处理后得到4 个邻接矩阵,即4 个图网络数据集。为降低后续工作的计算复杂度,设置节点的连接阈值为0.5,即当节点之间的相似度值低于0.5 时令相似度值为0,此时两个节点之间不存在连接。通过4 种计算方法得到图的结构信息,结果如表1 所示。本部分构建了基于不同相似度值的邻接矩阵,接下来将讨论各种相似度计算方法对链接预测模型的影响效果。
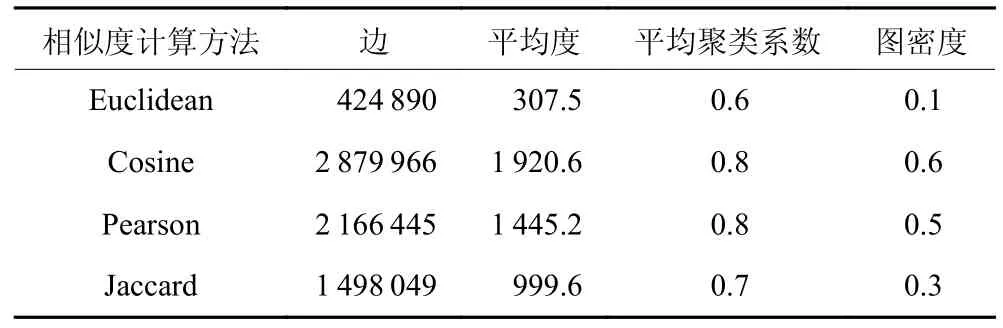
表1 制造服务资源图的结构信息Table 1 Structure information of graphs for manufacturing services
2 图神经网络模型与实验结果
2.1 图神经网络模型
本文采用邻居采样图神经网络模型 (graph sample and aggregate, GraphSAGE) 学习图的节点特征表示。该模型采用归纳式的节点学习方法,通过节点邻居采样的方式有效解决传统图卷积算法内存占用较大的问题,并且避免了节点的特征每次需要重训的情况,非常适合规模较大的图[16]。此外,最为关键的是其可以有效提升链接预测模型的准确度。
图1 为基于GraphSAGE 模型的制造服务推荐流程。该网络模型通过学习一个聚合函数来产生核心节点的特征表示。文献[16]证明长短时记忆 (long short-term memory, LSTM) 聚合器与池化 (Pool) 聚合器的性能更优,且在运行效率上Pool 聚合器效果更好,故本文采用Pool 聚合的方法进行节点表示。如式 (5) 和式 (6) 所示,首先对核心结点的邻居节点表示向量进行非线性转换,其次对转换后的特征表示向量进行池化操作。在此基础上,将池化后的结果和核心节点的特征表示各自进行非线性转化,最后,表示将两者转换后的结果进行叠加或者重组,以此来获得核心结点在这一层的特征表示。
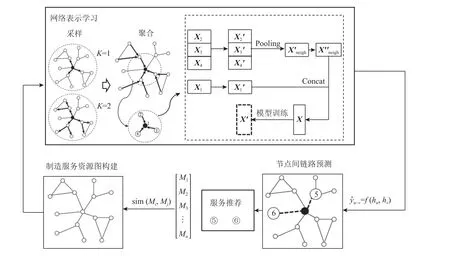
图1 基于GraphSAGE 模型的制造服务推荐流程Figure 1 Recommendation processes for manufacturing services based on GraphSAGE model
例如,如图1 所示,通过节点之间的链接预测得出节点⑤、节点⑥会与源节点产生连接,故将会向制造服需求商推荐节点⑤、⑥所对应的制造服务资源。
2.2 模型训练
神经网络模型的训练可以被视为在评估模型的输出值与真实值的差异后,通过损失函数来达到模型优化的过程。在这个过程中,激活函数、损失函数以及反向传播优化器的选择均会对最后的链接预测模型带来显著的影响。本节主要讨论激活函数、损失函数以及反向传播优化器的选择。
激活函数选择:在神经网络中加入激活函数可以向神经元中注入非线性因素,使得网络向任意非线性函数逼近[18]。文献[18]研究发现,线性整流激活函数 (rectified linear unit, ReLu) 可以加速模型的收敛,且能有效解决S 型激活函数 (sigmoid function)的梯度消失问题。ReLu 函数表达式见式(8),其中,x表示来自上一层神经网络的输入向量。
损失函数选择:目前推荐系统中应用较为广泛的损失函数分为单点法 (pointwise) 与配对法 (pairwise)[19]两种类型。Pointwise 类损失函数将推荐问题转化为多分类问题或回归问题,Pairwise 类损失函数将推荐问题转化为二元分类问题。由于本文将链接预测任务作为二元分类问题解决,所以Pointwise类损失函数将不再适用。为了提高训练过程中模型的收敛速度,本文采用二元交叉熵损失函数,定义如下。
其中,yˆu~v=f(hu,hv) 代 表在 模 型中 两 节点 之间存在连接的概率;1 -yˆ 则表示连接不存在的概率。此外,由于自适应矩估计 (adaptive moment estimation,Adam) 优化器具有计算高效、方便实现、内存使用少、可解释性强等优点[20],因此采用Adam 作为模型训练的反向传播优化器。
2.3 对比算法与评价指标
为了评价所提出的基于图神经网络的链接预测模型性能,以及证明模型的有效性,本文还对比了其他3 种链接预测算法。张健沛等[21]指出在诸多链接预测算法中,基于节点相似性的算法具有较低的时间复杂度,通过实验证明,共同邻居 (common neighbors, CN) 、Adamic-adar (AA) 与 资 源 分 配(resource allocation, RA) 算法具有较好的链接预测效果。3 种链接预测算法计算公式如下。
CN 算法:
其中, Γ (a) 表 示节点a的邻居节点集合;Γ(b)表示节点b的邻居节点集合; s im(a,b) 表示节点a和节点b的相似性;z表示节点a和节点b的共同邻居节点集合中的一个元素; Γ (z) 表示节点z的邻居集合。
本文采用AUC (area under the curve) 指标和精准度 (Precision) 指标来评估链接预测模型的准确性[22-23]。其中,AUC 指标是指在测试集中随机选择时,存在边所获得的分数值比不存在边所获得的分数值更高的概率。AUC 值定义如下。
其中,n表示所进行的实验次数;n′表示存在边比不存在的边拥有更高分数的次数;n′′表示两个分数值相等的次数。Precision 指标是指在网络的链接预测中,得分最高的前L条链接中预测正确的链接数m所占的比例。Precision 值定义为
AUC 值和Precision 值的大小反映了链接预测模型的准确性,其值越大说明预测模型的准确度越高。
3 分析与评价
首先,研究了不同相似度计算方法的链接预测模型对训练效果的影响,实验选取的节点数量为3 000,实验结果如图2 所示。其中,横坐标epoch代表训练的次数;纵坐标代表不同的性能评价指标,GraphSAGE-P、GraphSAGE-C、GraphSAGE-E和GraphSAGE-J 表示该链接预测模型是分别基于皮尔逊相关系数、余弦相似度、欧几里得相似度和杰卡德相关系数所构成的图网络上进行的。由图2可知,随着训练次数的增加,模型的AUC 值均呈现上升趋势,而Precision 值尽管出现了一定的波动,最终也逐渐收敛于较高水平,这表明模型取得了较好的准确度。与此同时,模型的损失值也随着训练次数的增加而快速降低且收敛,这表明模型获得了较高的预测性能。实验证明,基于GraphSAGE节点表示方法的链接预测模型在不同的相似度计算方法下均体现出较为优异的性能。
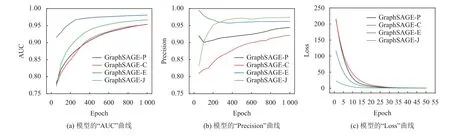
图2 不同相似度计算方法对应的链接预测模型性能Figure 2 Performance of the link prediction model using different similarity calculation methods
此外,还进一步研究了不同节点规模对模型的链接预测性能的影响,实验过程中模型的训练次数均为1 000 次,实验结果如图3 所示。结果表明,随着图的节点规模逐渐增大,模型预测性能出现一定程度上的波动,但从预测的Precision 值上可以发现,基于欧几里得相似度与杰卡德相关系数的链接预测模型表现较好,且能保持稳定。需要说明的是,由于损失曲线是为体现模型性能在固定节点规模下随训练次数的动态变化趋势,故此部分不探讨节点规模对模型的损失值的影响。
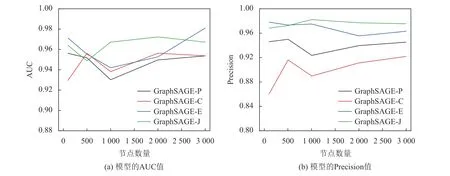
图3 不同的节点规模所对应的链接预测模型性能Figure 3 Performance of the link prediction model with to different number of nodes
在此基础上,为了评价所提出的链接预测方法的优劣,还将其与CN、AA、RA 3 种链接预测算法进行对比实验,实验中模型的训练次数为1 000次,实验结果如图4 与图5 所示。结果表明,本文所提出的链接预测方法均优于其他3 种链接预测算法。
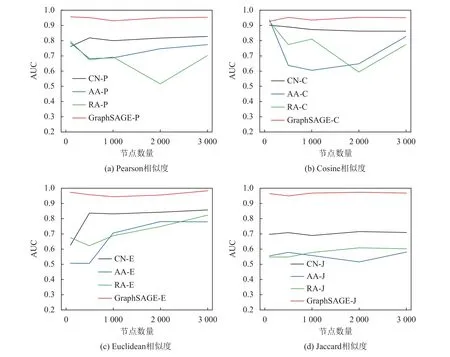
图4 不同链接预测模型的AUC 值Figure 4 AUCs of different link prediction algorithms
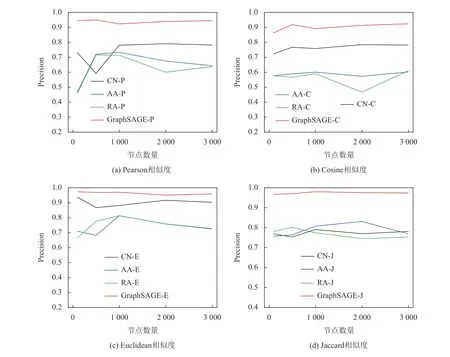
图5 不同链接预测模型的Precision 值Figure 5 Precision of different link prediction algorithms
结合图4 与图5 可知,无论是采用传统链接预测方法还是基于图神经网络模型的链接预测方法,在基于欧几里得相似度与杰卡德相关系数所构建的图上进行的链接预测,其性能优于另外两种相似度计算方法,且链接预测算法的AUC 值与Precision值在一定程度上均能维持稳定。对比表1 中不同相似度计算方法的图结构信息,发现基于欧几里得相似度与杰卡德相关系数的图网络具有较低的度与密度,这表明网络比较稀疏。这是由于本文设置了节点之间的链接阈值,若通过计算得出的相似度值低于阈值,则会被去除,从而保留下了相似度较高的链接。
本文认为,因为基于GraphSAGE 的节点表示方法是通过邻居节点聚合的思路进行,且每次聚合的邻居节点数为固定数值,所以当GraphSAGE 用于由欧几里得相似度与杰卡德相关系数所得到的图网络时,其聚合到的邻居节点与中心节点均具有较高的相似度,节点之间的链接关系较强。此外,相较于同一链接阈值下的其他相似度计算方法,避免部分弱相关性邻居节点带来的不利影响,去除冗余且弱相关性的链接,使得最终的链接预测模型获得较好的预测效果。
为了验证所提出的结论,在4 种相似度计算方法下进行不同链接阈值下模型链接预测效果的对比实验。如表2 所示,Ti表示不同的链接阈值设置。但是,由于本文节点的特征向量为01 向量,从而导致基于欧几里得相似度的计算方法所得到的相似度值,其值的大小不会出现在大于0.5 而小于1 的范围内。因此,从表2 中的数据可以发现,当阈值大于0.5 时,基于欧几里得算法的图的结构信息是不变的。为了更好地进行对比实验,本文针对欧几里得相似度添加阈值T0,T0等于0.2,此阈值下图的平均度为2 884.7,图密度为0.9。实验结果如图6与图7 所示。

图6 不同的链接阈值下链接预测模型的AUC 值Figure 6 AUCs of the link prediction model with different link thresholds

图7 不同的链接阈值下链接预测模型的Precision 值Figure 7 Precision of the link prediction model with different link thresholds
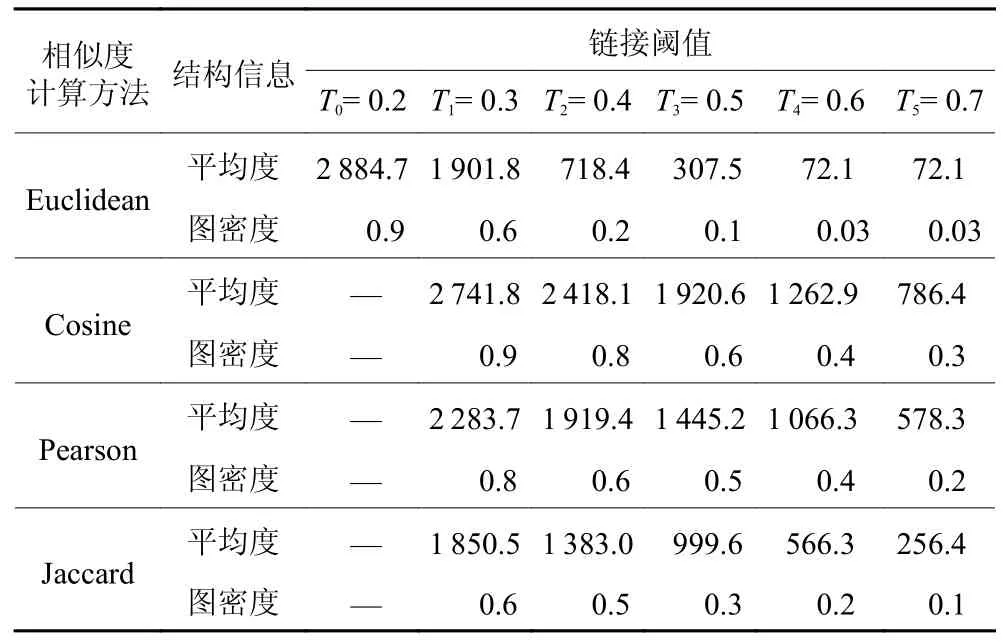
表2 不同链接阈值下的图结构信息Table 2 Graph structure information with different link thresholds
结果表明,在4 种相似度计算方法下,随着链接阈值的提高,链接预测模型的AUC 值与Precision值在整体上也呈现上升趋势,从而验证了上述结论。因此,可以在构建制造服务资源图数据集时,通过提高节点之间的链接阈值而提升链接预测模型的预测性能。具体而言,链接阈值的选择应位于大于0.5 而小于1 的范围内,从而使得链接预测模型取得较好的预测效果。
4 结束语
对云制造服务平台上的海量制造服务信息所带来的信息过载问题,提出一种基于图神经网络算法的云制造服务推荐方法。首先,该方法将云制造服务平台上的制造服务资源依据不同的相似度计算方法构建为图数据集。然后,利用GraphSAGE 进行资源节点的特征表示学习。最后,基于链接预测模型,预测出制造服务资源之间可能出现的链接情况,依据预测结果向用户推荐对应的制造服务。结果表明,在4 种不同相似度计算方法所构建的图数据基础上,基于图神经网络的链接预测模型均取得较好的链接预测效果,且预测性能优于所对比的CN、AA 以及RA 链接预测算法。此外,通过对模型的AUC 值与Precision 值进行分析,发现基于欧几里得相似度与杰卡德相关系数的链接预测模型性能要优于其他相似度计算方法下的模型。在此基础上进一步研究发现,在一定程度上,保留网络中相似度较高的链接可以显著提升模型的预测性能。
本研究尚存在一定的不足。例如,本文所推荐的制造服务类型相对比较独立,而在现实情况中,用户的制造服务需求可能是多样且复杂的。如何对复杂多样的制造服务需求进行制造服务的组合推荐,无疑是未来的一个重点研究工作。
