集成主成分分析与随机森林模型的关键工装寿命预测方法
2023-11-22朱晓峰徐曼菲刘治红冷杰武
朱晓峰,徐曼菲,刘治红,冷杰武
(1.广东工业大学 省部共建精密电子制造技术与装备国家重点实验室,广东 广州 510006;2.中国兵器装备集团自动化研究所有限公司 智能制造事业部,四川 绵阳 621000)
火工品是指一类用于引燃火药、引爆炸药的元器件和装置的总称,被广泛应用于工程爆破、武器弹药等领域。为了保证火工品的装配质量以及生产现场的人身财产安全,其生产过程需要有精密的工装以及安全可靠的生产工艺保证,工装是火工品质量与安全保证的关键资源。随着火工品装配线自动化程度的加深,关键易损工装的置换成为限制产线产能的瓶颈。因此,确保失效工装能够及时更换,不仅能够降低产品生产成本,减少返工品、次品、废品的出现,提高生产企业经济效益,还能保证生产现场的人身财产安全,从而提高火工品生产质量精益高效管控水平,为装配工艺的优化、工装的改进以及企业改进产品生产维护计划提供参考。
设备预测与健康管理 (prognostics and health management, PHM) 是保障系统安全运行的重要部分[1],剩余使用寿命 (remaining life span, RLS) 预测是PHM 的基础和核心部分[2]。剩余使用寿命预测主要是通过系统中监测传感器收集的数据来预测系统或系统要素的剩余使用寿命,预测的主要方法有基于物理模型、数据驱动以及混合模型的方法[3]。
随着各种机械设备精密化、复杂化程度越来越高,建立物理模型的难度越来越大甚至不能建立,而基于数据驱动的方法有不需要设备或产品的先验知识[4]的优点,因此基于数据驱动的方法越来越得到重视,主要包括统计模型方法、机器学习方法和深度学习方法[5]。其中,机器学习和深度学习的方法因其具有强大的数据处理能力,近年来在各领域已成为最流行的趋势之一[6]。李志刚等[7]运用RBF神经网络预测继电器的寿命,通过实例验证此模型具有较高的精度。Zhang 等[8]运用GA-BP 神经网络预测刀具寿命,实验结果表明GA-BP 模型的预测精度要优于标准的BP 模型。Liu 等[9]运用极限学习机、Ren 等[10]提出一种CNN-RNN 的方法、Chang等[11]运用基于多层网格搜索优化的LSTM 算法、Que等[12]运用GRU 算法对轴承的剩余使用寿命进行预测,通过实验证明上述预测模型均具有较高的预测精度。Wang 等[13]使用随机森林、Islam 等[14]提出一种改进CNN 模型对轴承故障进行诊断,判断准确率均能达到88%以上。Li 等[15]提出一种Elman-LSTM混合方法来预测电池的剩余使用寿命,最终的预测结果优于其他模型。Yao 等[16]提出一种基于支持向量机的锂离子电池故障诊断方法,能够高效地识别锂离子电池故障状态和程度。
基于机器学习的方法在刀具、轴承、电池等的寿命预测中得到广泛运用,但对于火工品装配关键工装的研究还较少。本文针对火工品装配过程中关键工装寿命预测困难、单一预测模型预测精度与效率不足和传统寿命预测模型易受噪声干扰等问题,提出一种基于主成分分析和随机森林的关键工装寿命预测模型。首先通过主成分分析,对工装环境、装配对象的特征和装配过程的工艺参数等多源数据进行特征提取,基于随机森林构建并训练关键易损工装的寿命预测模型,最后运用实际生产过程中产线的实时多源数据,监测并预测关键易损工装的健康状态,在生产中提前预测工装的剩余使用寿命,实现工装状态的精准管控。
1 关键工装数据及模型处理
火工品装配关键易损工装的寿命受到炸药药剂属性、装配工作环境、装配的工艺流程和工装的种类、形状、材料、工作温度、工作压力等因素的影响,使得工装寿命难以预测。目前很多企业仅仅从后序火工品装配质量检查中的外观检查来人工判断工装的更换时间,无法事先自动监测工装寿命。一方面,若工装更换过于频繁会造成企业资源的浪费,生产成本增加;另一方面,若没有及时更换工装则可能影响产品的质量及可靠性,增加返工品、次品、废品的数量,还可能会增加装配现场安全隐患。
如图1 所示,针对某火工品装配车间引信装配过程中关键易损工装寿命难以预测的问题,研究如何运用工装的各项参数、工装的装配对象特征、设备的各项参数以及产品装配过程中设备运行数据,如转速、拧紧力矩、压力、拧紧时间等多源生产数据预测工装剩余使用寿命。火工品装配关键工装寿命预测系统则对这些多源生产数据以及其他基础参数配置信息等进行分类储存。通过调用系统中的各项数据进行特征提取与模型训练,得到关键工装在不同使用环境、装配不同产品情况下的关键工装寿命预测模型。

图1 火工品装配关键工装寿命预测模型框架Figure 1 The framework of the life span prediction model for key fixtures in initiating explosive product assembly
1.1 关键工装寿命预测数据集
本文以某火工品装配车间的引信装配关键易损工装作为研究对象。在装配引信过程中,引信预拧机通过预拧工装夹持引信,将引信对准产品的待装配部位,保证两者间的同轴度要求后,旋转引信使产品与引信的内外螺纹相结合。引信拧紧机则使用拧紧工装夹持引信将引信拧紧到位。在引信装配过程中,要求工装提供恒定的夹持力,若工装夹持力过大将会使螺纹或引信表面受损;若夹持力过小则容易打滑,拧紧不到位的同时还会损伤引信表面。此外,引信与产品安装引信处还有同轴度精度要求,工装磨损后会导致同轴度精度超出许用范围,将可能导致引信偏心或螺纹烧死。为了满足防爆、不损伤零件表面、引信与产品的同轴度要求的同时提供足够摩擦力,引信装配工装采用橡胶与皮质材料定制而成,相比于金属工装,有着易磨损的特性,因此,每一个工装磨损到一定程度后都要停机并更换工装。
实验所用数据由某火工品装配车间4 台预拧机与4 台拧紧机共计消耗100 个关键易损工装的装配过程中,设备记录的历史健康数据以及人工测量并记录的工装、设备、产品和环境参数组成,如表1所示,包括设备、工装、产品和环境4 类影响因素共24 个特征。设备运行过程中每10 s 储存一组数据,实验所用的原始数据集包含13 090 组数据。

表1 关键工装数据集特征及特征意义Table 1 Features and their meanings of a key fixtures data set
1.2 数据预处理
关键工装寿命预测数据集对预测模型的构建有决定性的影响。在实际生产环境中,由于设备的一些偶然因素和人为因素等主客观因素的存在,关键工装寿命预测数据集可能会存在一些异常值。为了能让寿命预测模型更好地识别数据,提高预测的精度与效率,需要将数据集中包含的字符型数据转化成数值型数据,并统一数值型数据的量纲。因此,在构建寿命预测模型前需要对数据集进行预处理,主要包括异常值处理、字符型数据独热编码处理和特征标准化。
1.2.1 异常值处理
数据集中的异常值包括数据缺失和数值异常两种情况,这些异常数据不仅会导致数据集存在较大噪声,而且还会影响关键工装寿命预测模型的构建。处理异常值主要有删除异常值所在的数据条目和使用平均值、众数等数值替代两种方法,需要根据数据集特征的含义选择不同的方法,以提高数据质量。
在关键工装寿命预测数据集中,字符型数据一般为提前设定的各项固定参数,而数值型数据既有固定参数,又有监测生产状况的变化数据。为了尽可能保留原数据集所包含的信息,对于字符型数据的缺失,使用设备在一个生产周期内,对缺失值所属特征中众数最大的数据进行填充,使其与特征的主体保持一致;对于数值型数据的缺失或异常,首先删除异常值,然后使用设备在一个生产周期内,对缺失值所属特征的平均值进行填充或替换,使得填充或替换的数据能够尽可能接近真实值,减少异常值对寿命预测模型的影响。
1.2.2 独热编码
字符型数据存在不能被随机森林模型处理的问题,见表1 中“设备型号”特征为字符型数据。为了将字符型数据转化为数值型数据,采用独热编码的方式对“设备型号”列的数据进行处理,使用n位的状态寄存器对n类设备进行编码,编码完成后替换原数据列并直接接入原数据表,如图2 所示。
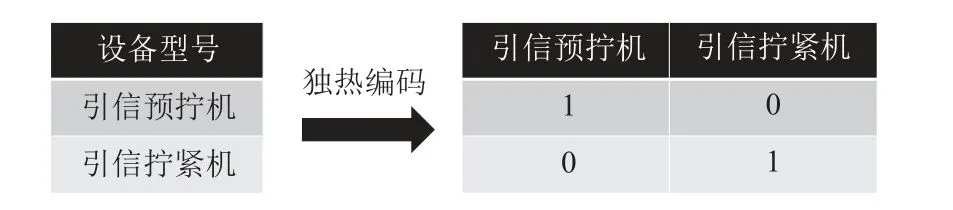
图2 字符型数据独热编码处理Figure 2 One-hot encoding processing of character data
1.2.3 标准化
为了防止数据样本中各项数据的大小差异性对预测结果产生影响,使用Z-Score 标准化将样本中不同量级的数据转化为统一量度的数据进行处理。根据初始数据集构建包含n行m列数据的初始矩阵Xn×m,通过式 (1) 对矩阵Xn×m的元素进行标准化处理,得到标准化矩阵。
1.3 关键工装寿命预测模型构建
关键工装寿命预测模型构建流程如图3 所示,主要概括为以下几个步骤。1) 利用生产过程中的多源 数 据的PCA 处理,得到 数据 集 特征 矩阵Xn×q;2) 构建关键工装寿命预测的模型并进行参数优化;3) 运用多源生产数据对工装剩余使用寿命进行预测。
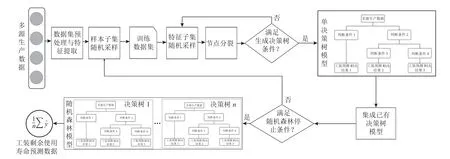
图3 关键工装寿命预测模型构建流程Figure 3 Construction processes of the life span prediction model for key fixtures
1.3.1 KMO 检验
KMO 检验主要应用于多源统计的因子分析,计算公式见式 (2)。KMO 统计量取值在0 和1 之间,当KMO > 0.5 就可以进行主成分分析,且取值越靠近1 越适合做主成分分析。
其中,rij和 αij分别表示变量i和j之间的简单相关系数和偏相关系数。计算关键工装数据集标准化矩阵24 种特征的KMO 统计量为0.833,说明样本适合进行主成分分析。
1.3.2 PCA 特征提取
主成分分析 (principal component analysis, PCA)是一种多变量分析技术,它的目标是从数据集中提取最重要的信息,并通过只保留这些重要信息来压缩数据集的大小[17],使问题得到简化,提高分析效率。对关键工装寿命预测数据集进行主成分分析的实现步骤如下所示。
1) 计算相关系数矩阵R。
其 中,rij为 列 向 量与 列 向 量之 间 的 协方差。由相关系数的定义式可知,数据集初始矩阵Xn×m的相关系数矩阵Rm×m即为。
2) 计算R的特征值和特征值向量。
求解特征值方程式 (5),计算得R的特征值λ1,λ2,···,λm( λ1≥λ2≥···≥λm) 和对应的特征值向量(ξ1,ξ2,···,ξm)。
3) 计算各特征的贡献率 ρ 。
根据式 (6) 计算出各个特征的贡献率 ρ 。
数据集中某一特征的贡献率 ρ 越大,表明该特征包含原始变量信息越多。在本文中,取累计特征量,确定前j个特征值对应的特征为数据集的主成分。

表2 数据集特征贡献率及累计贡献率Table 2 Contribution rates and cumulative contribution rates of features in a data set
1.3.3 随机森林模型构建
随机森林模型是基于决策树的一种集成学习算法[18]。相比于单决策树和传统神经网络算法,随机森林模型拥有可解释性强、计算效率高和分类与回归性能强等优点。随机森林模型是一种计算复杂度较低的模型[19],因此更适用于例如关键工装寿命实时预测等需要快速得到预测结果的场景。
在关键工装寿命预测数据集完成数据预处理及特征提取后,以数据集特征矩阵Xn×q作为输入数据开始构建随机森林模型。
步骤1 选择Python 作为关键工装寿命预测模型的开发编程语言,基于Keras 库构建。
步骤2 确定本文的随机森林模型中,以各个子节点的不纯度加权和G(xi,vij) 来衡量,评价切分特征与切分点的好坏,计算公式如式 (7) 所示。随机森林模型的决策树训练过程实际上是最小化G(xi,vij)的过程。
式中,xi为第i个切分变量;vij为切分变量xi的切分值;nleft、nright、Ns分别代表左子节点、右子节点、当前节点的训练样本个数;Xleft、Xright分别代表左子节点、右子节点训练样本的集合;yi表示当前节点样本变量;y¯left、y¯right分别表示左子节点、右子节点样本目标变量的平均值;H(X) 代表不纯度函数计算公式,本模型的预测目标为回归预测,H(X) 使用均方误差表示。
步骤3 对数据集特征矩阵Xn×q的行向量进行随机且有放回的重复抽样,生成样本矩阵Xp×q,而Xn×q中的行向量会有63.3%的概率被选中,其余未被选择的数据将作为袋外数据,以增加模型的鲁棒性与稳定性。
步骤4 在样本矩阵Xp×q的Q个列向量中,随机抽取q个列向量作为最优分裂节点候选 (q<Q)。对这q个列向量求解最小化不纯度加权和 m inG(x,v) ,选择最优切分变量x与切分点v,用选定的解(x,v)划分样本矩阵Xp×q为两个子集,生成两个子节点,并确定相应的输出值。
步骤5 以子节点中的数据集子集作为新的样本矩阵,对子节点递归执行步骤3,重复进行特征抽样以及节点分裂,直到样本集合样本矩阵Xp×q中的特征全部划分完毕,输出训练完成的单决策树模型。
步骤6 重复执行步骤2 ~ 4 生成多个单决策树模型,直至到达设定的最大决策树个数后,集成所有已生成的单决策树模型生成随机森林模型。
步骤7 关键工装寿命预测问题属于回归问题的一种,最终输出结果时,模型对m棵决策树的预测结果进行平均加权后,将得到的值作为模型预测结果并输出。
1.3.4 模型参数调优
为了进一步降低模型预测的泛化误差,避免模型过于简单或复杂,还需要进行参数调优。本文使用网格搜索的方式对随机森林模型决策树个数、最大树深度等关键参数进行调优,最终的调优结果如表3 所示。

表3 随机森林模型参数设置Table 3 Parameter settings of random forest model
2 模型预测结果与分析
2.1 十折交叉验证法
在一次随机森林模型训练的过程中,往往只使用一个训练集训练模型,定义一个损失函数计算模型偏离实际值的损失,用测试集测试模型的预测效果。然而模型在该测试集中取得最优不代表模型能在其他测试集中也能取得同样的效果。为了检验本文构建的关键工装寿命预测模型是否具有应用的普适性,采用十折交叉验证的方式对模型进行检验。将原始数据集随机地分为10 组,编号1 ~ 10,每组含有1 309 条数据,轮流选取其中的1 组作为测试集,其余9 组为训练集。查看模型在10 次实验中预测的准确性,求出10 次实验的平均准确率,以平均准确率评价模型预测的精准程度。
十折交叉验证实验结果如表4 所示。寿命预测模型在测试集中的准确率最高为93.81%,最低为93.1%,平均准确率为93.53%,在10 组实验中均有较高的预测准确性,验证了该模型在本次工装寿命预测实验中具有普适性。
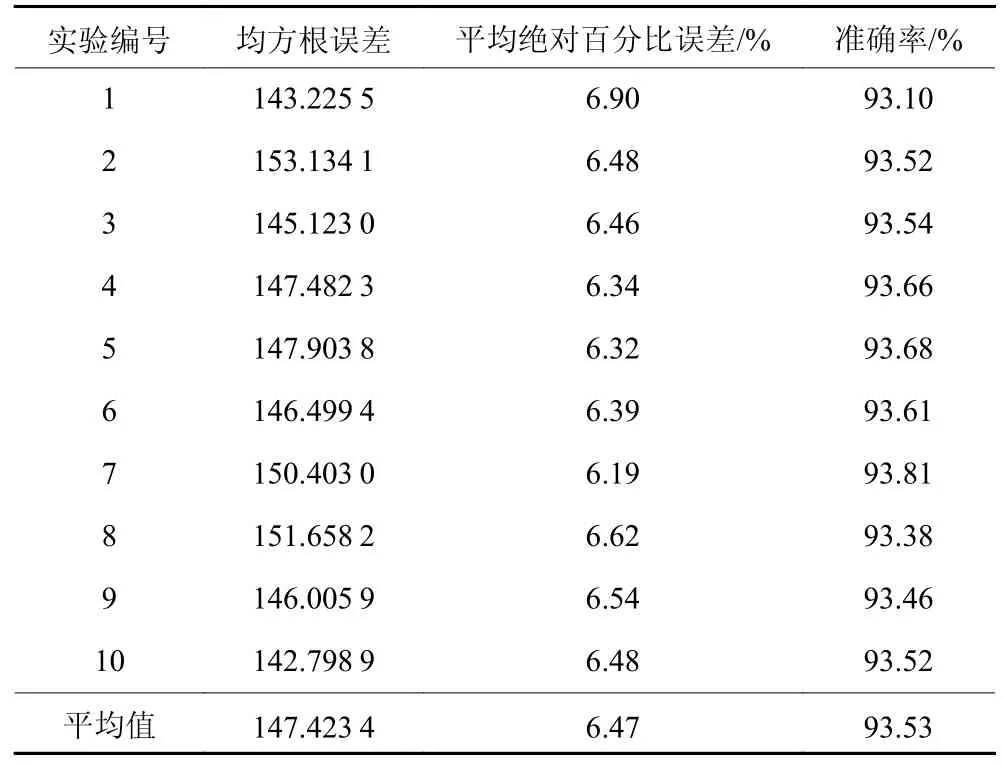
表4 十折交叉验证实验结果Table 4 Experimental results of ten-fold cross-validation
2.2 不同模型预测结果比较
为了进一步评估本文模型预测结果的准确性和有效性,分别采用本文模型、随机森林模型、BP神经网络模型、LSTM 模型和GRU 模型在实验1 条件下进行关键工装剩余使用寿命预测,所用的5 种模型均使用Python 编程语言实现,并基于Keras 库构建。预测结果比较如表5 所示,平均绝对百分比误差最小为本文模型的6.39%,最大为BP 神经网络模型14.02%;均方误差与均方根误差最小为本文模型的4.05 和146.50,最大为GRU 模型的10.30和372.51;预测时间最短为本文模型的9.80 s,最长为LSTM 模型的211.19 s。本文提出的关键工装寿命预测模型较单纯随机森林模型准确率提升了0.89%,均方误差、均方根误差和预测用时分别降低22.3%、22.3%和24.8%。
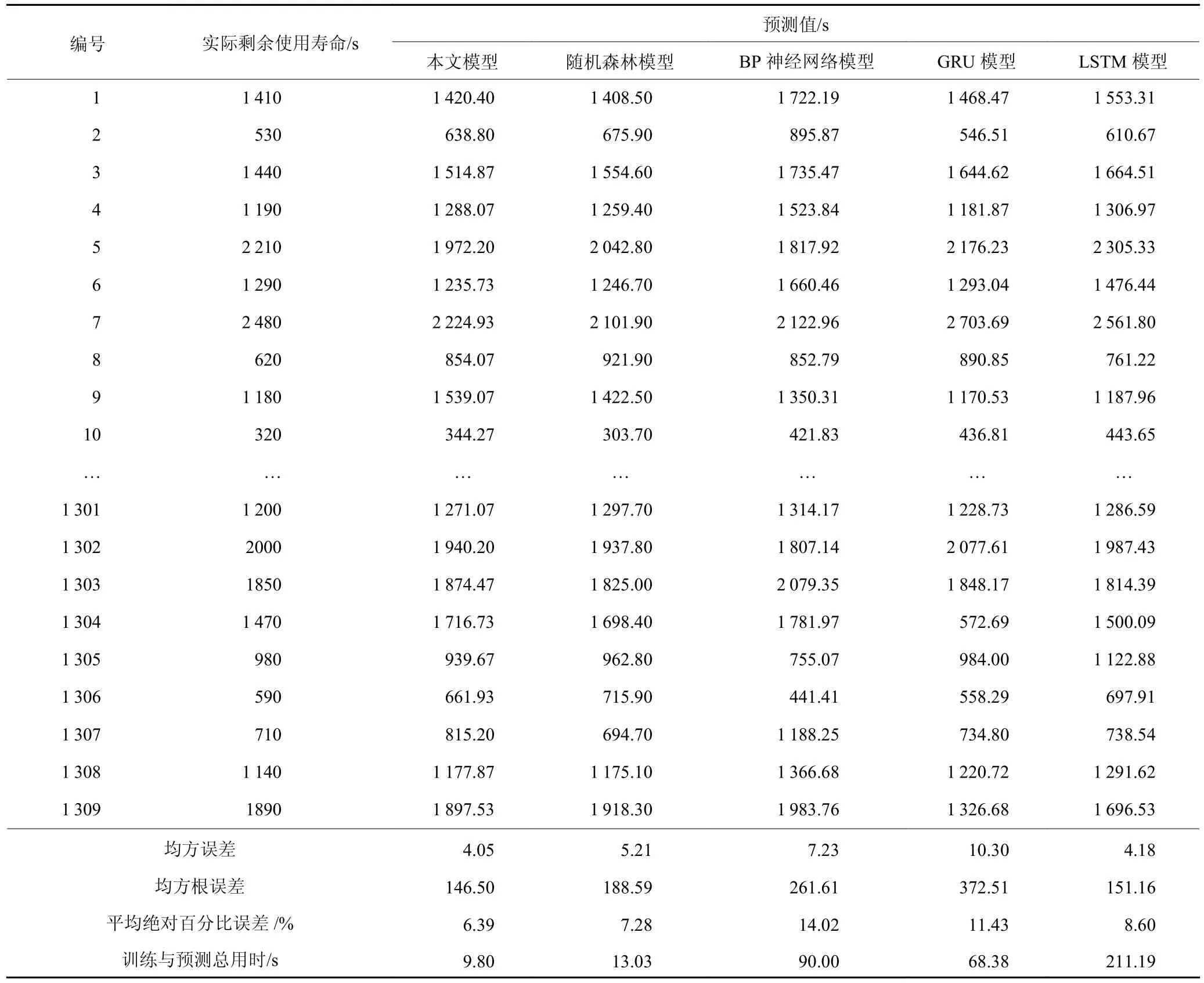
表5 本文模型与其他模型预测效果评价Table 5 Evaluation of effectiveness among the proposed model and other models
选取测试集中7 个工装的110 组数据,为了能更好地体现不同模型对数据集的拟合情况,将这110组数据分别按工装顺序与剩余使用寿命从大到小的顺序进行排序,5 种模型对这110 组数据的预测结果比较如图4 所示。工装剩余使用寿命大于2 000 s时,本文模型和随机森林模型预测结果偏小;工装剩余使用寿命小于2 000 s 时,与真实值的拟合效果较好。BP 神经网络模型与GRU 模型预测结果不稳定,预测值围绕真实值波动相比其他模型较大。LSTM 模型预测结果比较稳定,但预测结果较真实值偏大。综上分析,本文模型与随机森林模型对工装实际剩余寿命拟合效果更好且更稳定。
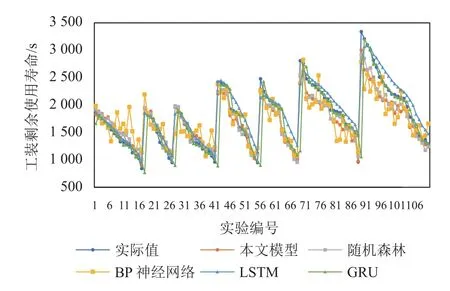
图4 本文模型与其他模型的预测结果Figure 4 Prediction results using the proposd model and other models
通过表5 与图4 的比较可以证明,本文模型较其他传统预测模型,在关键工装寿命预测中具有较高的剩余使用寿命预测速度、精确度与稳定性,能够更好地契合实际生产情况中,需要响应速度快、预测精度与稳定性好的要求。这进一步证明了本文提出的关键工装寿命预测模型的准确性与有效性。
3 关键工装寿命预测系统
3.1 系统体系架构
针对当前火工品装配车间关键工装状态掌控难、引信装配综合效率低、信息记录、查看工装效率低下等影响质量问题,开发了火工品装配关键工装寿命预测系统,体系架构如图5 所示。将现场多源数据管理模块、数据显示模块、用户操作请求模块、关键工装寿命预测参数配置模块以及关键工装寿命预测模块进行集成,以满足不同使用者的需求。
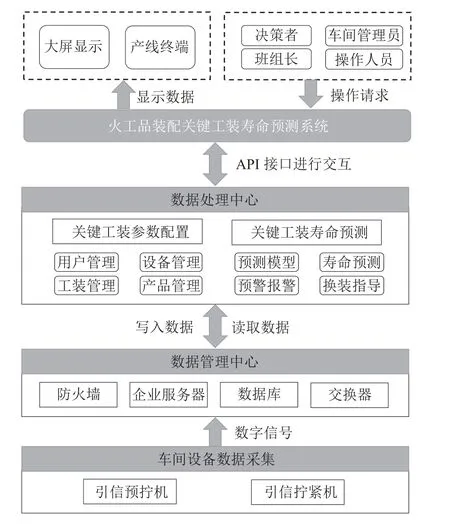
图5 火工品装配关键工装寿命预测系统体系架构Figure 5 Architecture of a life span prediction system for key fixtures in initiating explosive product assembly
3.2 系统总体运行流程
如图6 所示,在火工品装配过程中会产生设备、工装、产品的多源数据,多源数据经过处理后储存至服务器中,关键工装寿命预测模型则调用生产过程中的多源历史数据进行训练,模型训练完成后储存至数据库中。
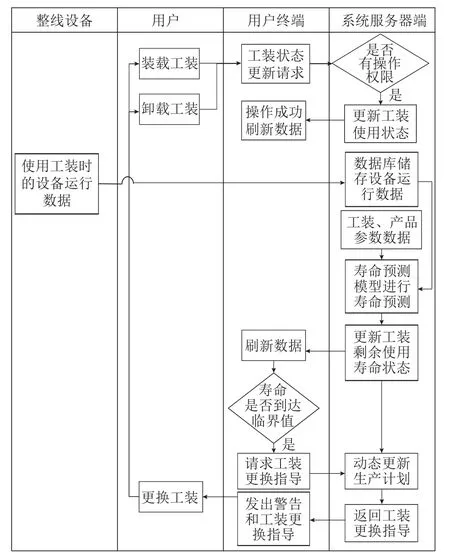
图6 关键工装寿命预测系统运行流程Figure 6 Operation processes of a life span prediction system for key fixtures
在火工品产线实际生产时,生产设备将会向服务器端发送实时数据,服务器端根据当前生产信息调用已进行训练的模型对输入数据进行计算,并输出工装预测剩余使用寿命,储存至数据库中。同时服务器端也将实时监控各个工装的剩余使用寿命,当工装剩余使用寿命到达临界值后向用户发出预警并生成工装更换指导,待工装达到废弃标准后,用户停机更换工装并更新设备和工装数据。
此外,用户还可以对设备、工装、产品的各类信息进行查询、增加、删除、修改操作,服务器端识别用户身份后处理用户请求,并返回更新数据和用户的操作结果。
3.3 系统实现
根据关键工装寿命预测的需求,基于图5 所示的体系架构,本文设计了火工品装配关键工装寿命预测系统。该系统采用B/S 架构,可分为展示层、业务逻辑层和数据交互层,便于用户进行各项操作,同时便于系统后续维护和扩展。系统中的展示层使用JavaScript 语言基于Vue 框架实现,业务逻辑层使用Java 语言基于SpringBoot 框架实现,数据库使用Mysql 数据库。
如图7 所示,关键工装寿命预测系统主界面由看板系统、工装信息管理、设备信息管理和产品信息管理4 个界面构成。其中,看板系统将调用关键工装寿命预测模型对工装的剩余使用寿命进行预测,根据其预测结果来判断设备的状态,并根据工装状态使用绿、橙、红色标签表示并统计设备健康、预警、警告状态。其余信息管理模块实现在火工品装配过程中动态信息与静态信息分类储存管理的功能。
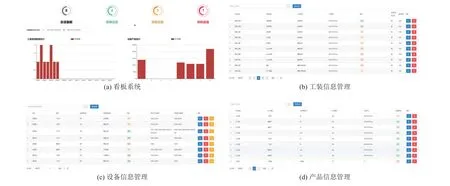
图7 关键工装寿命预测系统界面Figure 7 The interface of a life span prediction system for key fixtures
通过基于火工品关键工装寿命预测模型的系统原型,实现了在不同工况下各个工装寿命的实时预测与监控,为现场人员更换工装提供决策依据,能有效减少返工品、次品乃至废品的出现,提高车间效能。
4 结论
通过构建结合主成分分析和随机森林的关键工装寿命预测模型及系统原型,可得出以下结论。
1) 本文模型通过结合主成分分析和随机森林,对多维的关键工装历史健康数据进行分析并提取数据的主成分,降低了数据噪声对预测模型构建和预测结果精度的影响,降低了寿命预测过程中数据计算的复杂程度,提高寿命预测的准确率与效率。
2) 通过实验证明,相较于其他常用的预测模型,本文模型不仅提高预测精度,还提高了预测数据输出的稳定性,减少了预测时间。
3) 基于本文提出的火工品装配关键工装寿命预测系统体系架构,开发了火工品装配关键工装寿命预测系统原型,实现对寿命预测相关的工装、设备、产品参数的管理,以及产线中各个工装剩余使用寿命的实时监控,为现场人员更换工装提供决策依据。
