例析高考中直线与圆相切问题

袁海军

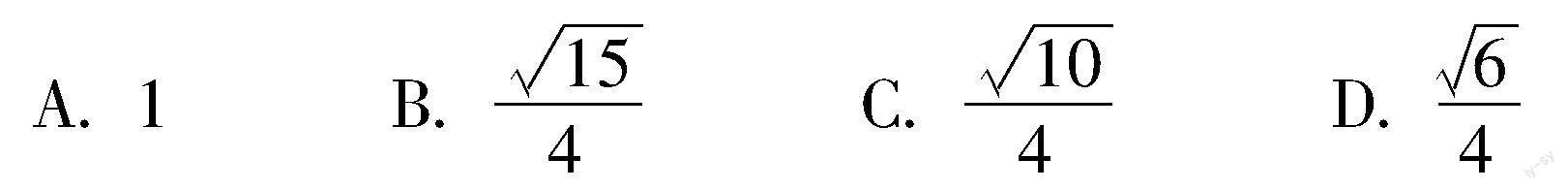
引例.（2023年新高考全国1卷第6题）

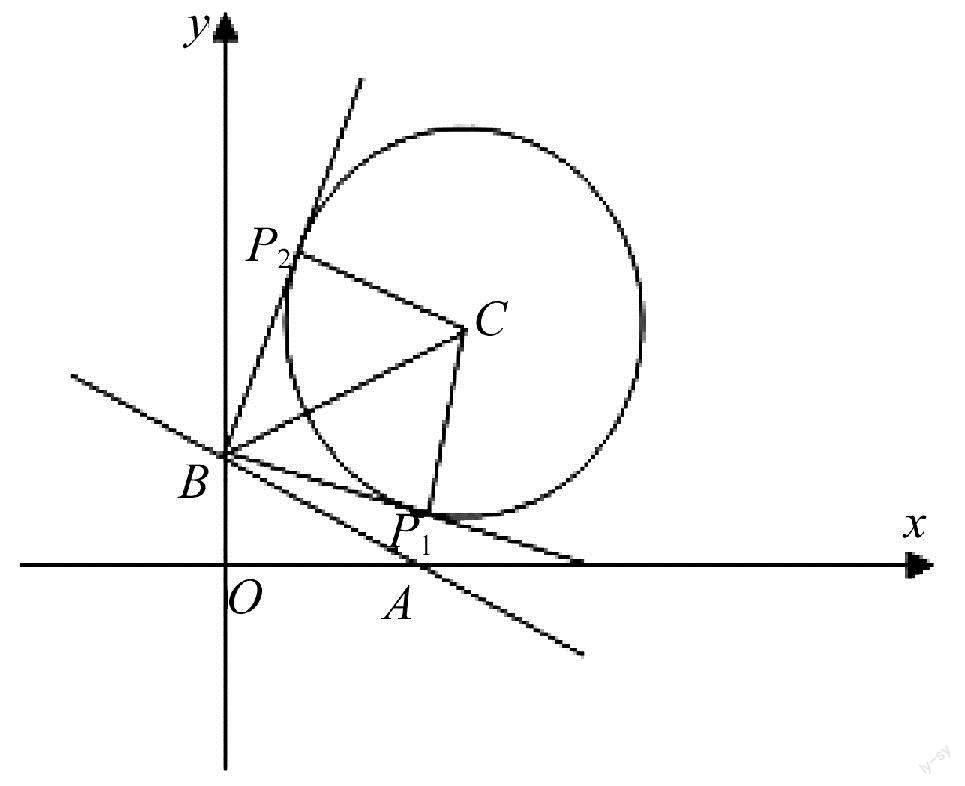
过点（0，-2）与圆x2+y2-4x-1=0相切的两条直线的夹角为α，则sin α=（）

答案：B.

解析：本题考查了直线与圆的位置关系，重点考查相切问题，以下从三个角度来进行求解：

点评：本题考查了直线与圆的位置关系，重点考查相切问题，可从切线方程、切线长，切点三角形等方面入手，其难度不大.此题的解法相对容易，属常规思路通法求解，思路一：根据切线的性质求切线长，转化到切点三角形的一个内角，并结合二倍角公式运算求解；思路二：根据切线方程结合点到直线的距離公式可得k2+8k+1=0，利用韦达定理结合夹角公式运算求解；思路三：根据切线的性质求切线长，转化到有公共边且对角互补的两个三角形，再结合余弦定理运算求解．

针对此题我们来进一步探讨有关直线与圆的相切问题：

1.定义：直线与圆只有一个公共点.

2.方法：几何法：圆心到直线的距离d等于半径长r，即（d=r）.

代数法：联立直线与圆的方程，消元后得到关于x（或y）的一元二次方程，方程有唯一的实数解，即（Δ=0）.

3.基本类型：

（1）求过圆上的一点（x0，y0）的切线方程：

（2）求过圆外一点（x0，y0）的圆的切线方程：

①几何方法：当斜率存在时，设为k，则切线方程为y-y0=k（x-x0），

即kx-y+y0-kx0=0.由圆心到直线的距离等于半径长，即可得出切线方程.

②代数方法：当斜率存在时，设为k，则切线方程为y-y0=k（x-x0），即y=kx-kx0+y0，代入圆的方程，得到一个关于x的一元二次方程，由Δ=0，求得k，切线方程即可求出．

（3）在求过一定点的圆的切线方程时，应首先判断定点与圆的位置关系，若点在圆上，则该点为切点，切线只有一条；若点在圆外，切线有两条；若点在圆内，则切线不存在．

4.常用结论：

①过圆x2+y2=r2上点P（x0，y0）的圆的切线方程为x0x+y0y=r2.

②过圆（x-a）2+（y-b）2=r2上点P（x0，y0）的圆的切线，

方程为（x-a）（x0-a）+（y-b）（y0-b）=r2.

③过圆x2+y2=r2外一点P（x0，y0）作圆的两条切线，则两切点所在直线（切点弦），

方程为x0x+y0y=r2.

④过圆（x-a）2+（y-b）2=r2外一点P（x0，y0）作圆的两条切线，则两切点所在直线（切点弦）方程为（x-a）（x0-a）+（y-b）（y0-b）=r2.

下面我们再来看近几年的四道高考原题，并从多维度，多方法进行分析与求解．

例1.（2023年高考全国乙卷文数第11题）

已知实数x，y满足x2+y2-4x-2y-4=0，则x-y的最大值是（）

答案：C.

解法1：判别式法

解法2：几何法

解法3：三角换元法

点评：本题作为选择题的第11题，言简意赅，方法明确，难度中档.看似是一个求函数最大值问题，其本质是考查直线与圆的相切问题，要求考生学会将函数问题转化为解几问题，并结合直线与圆的相关知识，利用几何法，代数法进行求解.思路一：令x-y=k进行代入消元，利用判别式法即可；思路二：通过整理得（x-2）2+（y-1）2=9，利用三角换元法即可，思路三：整理出圆的方程，设x-y=k，利用圆心到直线的距离小于等于半径即可．

例2.（2021年新高考全国Ⅰ卷第11题）

已知点P在圆（x-5）2+（y-5）2=16上，点A（4，0），B（0，2），则（）

A.点P到直线AB的距离小于10

B.点P到直线AB的距离大于2

答案：ACD.

点评：本题作为多项选择题，要求考生考虑全面，逐项论证.此题表面上考查动点到定直线的距离和动直线与定直线夹角的最值问题，其本质还是考查直线与圆的相切问题，要求考生学会将最值问题用极端位置法处理，利用图形简单明了.

例3.（2020年高考全国新课标1卷理数第11题）

已知⊙M：x2+y2-2x-2y-2=0，直线l：2x+y+2=0，P为l上的动点，过点P作⊙M的切线PA，PB，切点为A，B，当|PM|·|AB|最小时，直线AB的方程为（）

A.2x-y-1=0B.2x+y-1=0

C.2x-y+1=0D.2x+y+1=0

答案：D

解法1：公共弦法

以MP为直径的圆的方程为（x-1）（x+1）+y（y-1）=0，即 x2+y2-y-1=0，两圆的方程相减可得：2x+y+1=0，即为直线AB的方程. 故选：D．

解法2：切点弦法

由公式可得P（-1，0）的切点弦方程为（xP-1）（x-1）+（yP-1）（y-1）=4，即AB的方程为：2x+y+1=0. 故选：D．

点评：本题主要考查直线与圆的位置关系，最值问题，破解此题的关键是会转化，即把|PM|·|AB|的最小值问题层层转化，最终转化为|PM|的最小值，从而转化到点到直线的距离的最小值问题.考查的核心素养是逻辑推理，直观想象，数学运算.在思路二中直接采用切点弦公式求解，需巧记将圆方程的两变量各“代一半”的模式.

例4.（2022年新高考全国1卷第15题）

写出与圆x2+y2=1和（x-3）2+（y-4）2=16都相切的一条直线的方程 ．

解析：圆x2+y2=1的圆心坐标为O（0，0），半径r1=1，圆（x-3）2+（y-4）2=16的圆心坐标为C（3，4），半径r2=4，如图：∵|OC|=r1+r2，∴两圆外切，由图可知，与两圆都相切的直线有三条．

∴与圆x2+y2=1和（x-3）2+（y-4）2=16都相切的一条直线的方程为：

x=-1（填3x+4y-5=0，7x-24y-25=0都正确）．

故答案为：x=-1（填3x+4y-5=0，7x-24y-25=0都正确）．

点评：本题考查两圆的公切线问题，要先判断两圆的位置关系，再结合直线与圆相切的几何意义，分情况讨论即可.此题因为两圆是外切，它有三条公切线，通过作图观察其中的一条比较容易求出.这也是开放型试题的一个优点，要求考生快速求出一个答案即可，不要求全面求解．

巩固练习题

（1）求过点P的圆C的切线方程；

（2）求过点M的圆C的切线方程，并求出切线长．

2.设m，n∈R，若直线（m+1）x+（n+1）y-2=0与（x-1）2+（y-1）2=1 相切，则m+n的取值范围是．

3.在平面直角坐标系xOy中，已知圆C：x2+（y-3）2=2，点A是x轴上的一个动点，AP，AQ分别切圆C于P，Q两点，则线段PQ的取值范围是．

参考答案：

参考答案：

1.解析：由题意得圆心C（1，2），半径长r=2．

（2）因为（3-1）2+（1-2）2=5>4，所以点M在圆C外部．

当过点M的直线斜率不存在时，直线方程为：x=3，又点C（1，2）到直线x=3的距离d=3-1=2=r，所以直线x=3是圆的一条切线．

当切线的斜率存在时，设切线方程为y-1=k（x-3），即y=kx-3k+1，