深刻理解概念才能解答好数学问题
2023-11-22俞新龙
俞新龙


如果说2022年新高考数学Ⅰ卷第18题颠覆了“高考题中三角大题是送分题”的认识,那么2023年新高考数学Ⅰ卷第20题则教训了“新高考Ⅰ卷数列大题不会成为难题的师生观”,综合考生答题情况看,2023年的数列大题成为许多考生的“拦路虎”,甚至成为“送命题”.造成这种情况的原因是什么?能给新一年的高考复习带来怎样的教学启示?
一、高考题及解答
(1)若3a2=3a1+a3,S3+T3=21,求an的通项公式;
(2)若bn为等差数列,且S99-T99=99,求d.
注意:從qt=0不难发现,若两个等差数列通项公式之积是关于n的无常数项的二次函数,则这两个等差数列通项公式必定有一个是关于n的无常数项的一次函数,有一个是关于n的有常数项的一次函数.
二、造成解题困扰的原因探析
从考试结束后全国各地考生普遍反馈2023年新高考Ⅰ卷试题相比前三年容易,但却一致认为数列大题出乎意外给自己难住了,或者根本找不到解题思路,失去了“应该得到的分数”.我们认为,主要是以下两方面的原因.
1.被数列大题位于第20题进行了心理上的打击.新高考Ⅰ卷前面3年数列大题分别位于第18题(2020年)、第17题(2021年和2022年),再加上在平时高考复习中师生心理预期都是一致认为数列大题不会难,大概率属于中档以下问题,但2023年数列大题却一下子成为倒数第3题,并且题中条件“似乎比较新颖”,无形中加深了考生的心理恐惧,增加了解题紧张,影响了解题发挥.
2.缺少深刻理解数学概念.数学概念是比较枯燥乏味的,除了新学习时直面概念外,在其他复习时间都少有再认真对待数学概念的时候,学生宁愿多做数学题也不愿意回归教材理解概念是常态,在复习中教师大多数也仅是投影概念,缺少深入挖掘相关概念的内涵和外延.于是,在平常复习中一些习得的解题方法只是表面看起来会了,稍有变化(情境改变、知识交叉等)就只能无可奈何.
四年高考新高考Ⅰ卷在“去套路化”方面做出了成功尝试,命题更加重视考查考生对基础知识的理解,尤其是对数学概念的深刻理解,所以第二个原因更加值得我们重视并努力去改变和提高.
三、数列高考题身影探析
如前所述,没有比较完美解答2023年数列大题主要原因是缺少深刻理解等差数列通项公式和前n项和公式这两个概念,因为无论是在教材还是在平常习题中都有类似“身影”呈现.
1.普通高中教科书数学选择性必修第二册(A版)《4.2.1等差数列的概念》在推导得到通项公式an=a1+(n-1)d后有一个“思考”栏目,探讨了等差数列通项公式与一次函数的关系.
3.常见习题:
(1)已知等差数列{an}、{bn}的前n项和为Sn、Tn,若
其实2023年新高考Ⅰ卷选择题7也是考查等差数列的通项公式是关于n的一次函数和等差数列的前n项和是关于n的没有常数项的二次函数,如果深刻理解了等差数列概念的这两个结论,则马上就会得到答案C.
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
题在书外,根在书中.华罗庚先生“厚-薄-厚”是学习数学概念经典概括,只有把概念领悟透彻,我们做题时才能够以概念实质去应对具体题目的变化形态,这与孔子说的“学而不思则惘,思而不学则殆”是一致的.
四、要把握高考题对高考复习的指导作用
其实2020~2023年新高考Ⅰ卷中每年均有一定量试题是考查概念的,只不过有些是比较明确的,有些是比较隐蔽的,缺少的是我们探究发现的眼光和行动,例如2020年新高考d卷第20题立体几何大题就在隐性提醒我们要特别注意对教材中直线与平面所成的角这个概念进行深刻理解.
2020年新高考Ⅰ卷20题:如图1,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
解析:(1)因为AD//BC,AD平面PAD,所以BC//平面PAD,有线面平行性质知l//BC.因为PD⊥BC,CD⊥BC,PD∩CD=D,所以BC⊥平面PDC.因此,l⊥平面PDC.
因为高考题具有比较好的空间直角坐标系结构,所以绝大多数都会选择向量坐标方法求解,鲜有常规几何法求解,这就造成了一种错觉:常规几何法无法求解高考题,或者说这样就掩盖了常规几何法的精妙,这就是由于对教材中相关概念理解不到位、不深入造成的.
人教A版必修第二册151页:
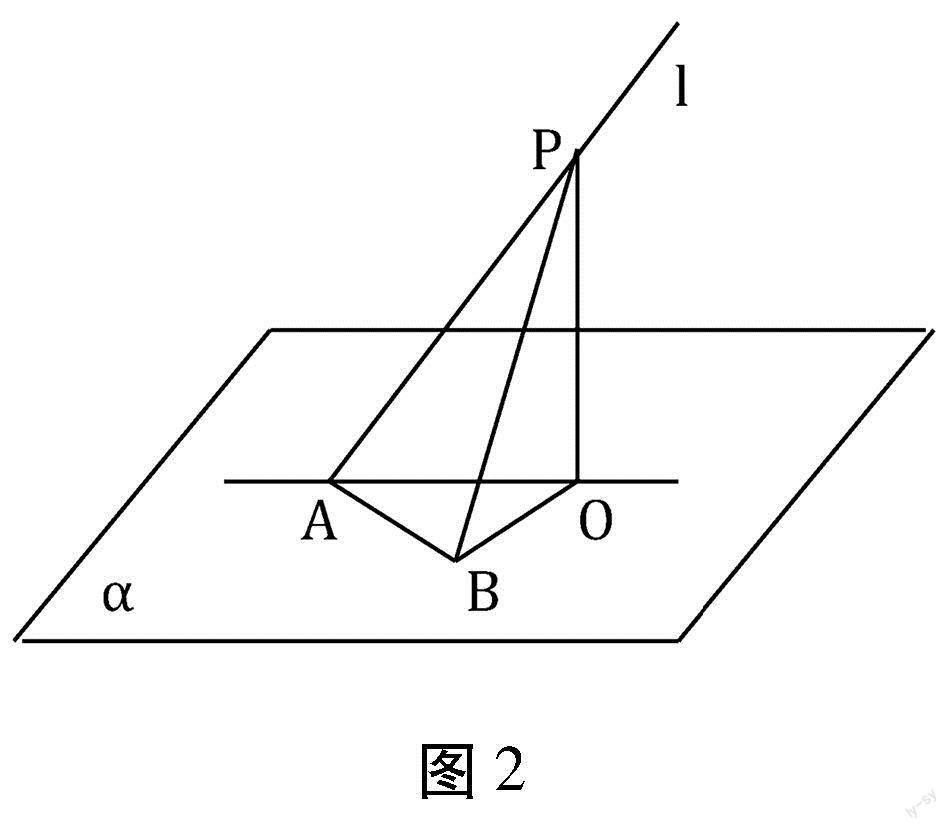
如图2,一条直线l与一个平面α相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
(2)如图3,另有一包含直线AB的平面β,若PO1⊥β,作O1b1⊥Ab1,所以∠PAO1<∠PAB.这就告诉我们,∠PAB比直线l与经过直线AB的任意平面所成的角都要大;进一步可以知道,若另有一条平行于直线AB且与直线l异面的直线CD,则异面直线l与CD所成的角是直线l与经过CD的任意平面所成角的最大角.
呢?从前面定义内涵知,此时∠PBA就是直线PB与平面QCD所成的角,如图4,平面QCD∩平面PAB=MN,根据题意可知AB//MN,所以∠PBA=∠PNM,即∠PNM应为直线PB与平面QCD所成的角,则此时MN应是直线PB在平面QCD上的射影,即应该有PM⊥平面QCD,故可得PM⊥QD,再注意到PD=AD=1,PD⊥AD,l//AD,所以四边形ADPQ只能是正方形,因此,PQ=1.
数学教材是学习数学知识的蓝本,大多数知识都是显性呈现的,但也有相当一部分知识是隐性呈现的,需要我们去努力挖掘找出来,即特别要重视教材知识发生的核心要义,即知识的内涵与外延.
五、深刻理解概念永远在路上
大家都认同高考题对教学的指挥棒作用.所以说,教材中每一个概念都需要我们去认真对待并深入理解,许多时候我们自认为对某一个概念已经理解得比较好了,但实际上远远没有到深刻理解的程度.下面我们通过2023年高考复习中一个比较典型的例子来提醒.
解析:首先要找出多边形Γ在顶点D1处的内角,怎么找?利用基本事实2(如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内)和基本事实3(如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线).如图5,延长D1M和DA相交于点G,则易得AG=AD,连接GN交BC于
概念理解永无止境;深刻理解概念永远在路上.
李邦河院士在2009年4月荣获华罗庚数学奖并作报告时指出:“数学根本上是玩概念的,不是玩技巧.”概念不是学习时重要,解题时不重要,概念是“万丈高楼平地起的地基”,只有深刻理解数学概念才能解答好数学问题,让我们始终牢记概念、深入理解概念.
