基于改进Nelder-Mead 算法的井位优选方法

2023-11-22张佳亮葛洪魁申颍浩叶智慧

西华大学学报（自然科学版） 2023年5期

张佳亮，陈冬，葛洪魁，申颍浩，叶智慧

（1.中国石油大学(北京)非常规油气科学技术研究院,北京 102249；2.中国石油大学(北京)石油工程学院,北京 102249；3.中国石油大学(北京)安全与海洋工程学院,北京 102249）

井位优选是油气田开发过程的重要一步，直接影响钻井、压裂和生产的成本与风险[1]。特别是，在自然造斜能力差的高陡倾角地层，防斜打直控制难度高、地质脱靶风险大；在非均质性强、可压性低的非常规储层，储层改造难度大、作为油气渗流主要通道的复杂缝网难以均匀形成[2]；在地面地貌复杂的区域，井位部署受到极大制约[3]：因此，在油气开采过程中，优选井位具有重要意义[4]。国内外众多学者和工程师就井位优选与部署进行了大量研究，井位优选方法主要包括以下几种。

1）优选甜点区是优选井位最直接的方法。井筒连通地质甜点是油气藏高效、经济开发的关键，将地震、测井、地质和油气藏工程结合，综合采用各类地质与工程动静态资料，优选富含油气区，继而优选出井位[5-7]。此外，针对非均质性气藏，充分将地震与地质相结合，可精细刻画非均质、微裂缝发育气藏小层、构造、沉积和砂体展布特征，并对地层的地震相干属性、曲率属性和蚂蚁体属性进行分析，或对地震波进行优势波形结构精细分析及反演，进而确定含气富集区内的井位[8-10]。该方法目标性强，主要通过分析地质属性确定甜点来优选井位，但忽略了工程因素，有相当大的局限性。

2）通过对特征参数进行模糊数学分析，在指标分析的基础上优选出离散有限点位的井位。这在特定功能井的选择上应用较多。储层厚度、TOC、含油/气饱和度、脆性、可压性、孔隙度、渗透率、地层压力、井控储量、可动油量、原油密度、原油黏度、储层温度等是主要指标参量。在中牟页岩气区块，对5 个储层指标进行数据处理和叠加，钻井压裂后气测显示良好[11]；在J 油田稠油提液井优选中，对9 个储层指标进行模糊分析，通过对各指标的权重和隶属度相乘得到综合模糊评价值，进而优选出提液井位[12]；在复杂断块高含水油藏加密井位优选中，将剩余可动油量、最深的油层深度、油层平均渗透率、平均含油饱和度、油层厚度/有层数等权重分别设为0.45、0.05、0.15、0.3、0.05，并应用在大港油田，其效果较好[13]；在煤层气井位优选和CO2吞吐井位优选中，分别对6 个指标和11 个指标进行模糊分析，并应用在韩城地区和东部W 油田，其效果较好[14-15]。此外，在页岩气地质调查井位优选中，林腊梅等[16]对11 个地质指标和7 个工程地质条件指标进行了分级和模糊数学计算，得到了5 口分析井的综合评价分值。这种方法主要适用于对有限个备选井进行特定功能井的优选，或将地层离散成有限个可能的井位进行的优选，或在老井挖潜增产中。

3）数值模拟是优选井位的有效方法。通过数值模拟可以快速计算不同位置布井的产量，近年来该方法在国内外应用较多。不同的模拟器求解精度与效率不同，其中算法和控制方程是主要的制约因素和难点。为提高计算能力同时针对地质工程数据量巨大等特点，近年来神经网络算法被应用于井位优选[17-21]。这种方法逐渐成为主流，便于井位的经济评价，但其要求精准，对储层建模工作量较大，成本较高。

4）在工程实践中，往往需要将地质甜点、地形地貌和工程经济性等综合考虑，经过多轮次筛选逐步确定最佳井位。在苏6 与苏36-11 区块水平井位选择时，根据沉积相，发现水平段与河道方向一致时，水平井实施效果比较好[22]；在子洲气田山2 气藏增产开发中，先通过地质特征筛选有利区，然后从经济角度确定井网，最后结合有利区及砂体展布确定了最佳井位[23]。在工作流程上，主要采用“多梯次”踏勘的方法优选井位，它包括3 个阶段：井位意向阶段、井位确定阶段和井位批准后阶段。这种方法需要多梯次组织相关人员进行实地探勘并确定井位[24]，具有较强的实战意义，但是相对粗放、对经验的要求较高且工作量较大。

当前：基于实地踏勘的“多梯次”定井位方法，相对粗放且工作量巨大；基于“瞄准”甜点的优选方法，忽略了部分工程因素，特别是地貌复杂、存在约束区的情况；基于统计规律的数学模糊方法，过分依赖数据的准确性和数量；数值模拟优化选井位方法，以兼顾地质工程因素、高效和低成本的特点，越来越多地被采用[25]。众多优化算法[26-30]中，无梯度优化算法是处理数值模拟优选井位的主流算法，主要是因为地质储层特征在空间分布上呈强非均质性，往往局部会出现高梯度或无梯度的特征。Nelder-Mead 优化算法通过对目标函数值比较，确定优化方向，非常适合井位优化工作，但该算法在反映计算时，反映点较远，可能会降低收敛速度，并且无法进行约束优化，在避让特定区域时，可能失效[31]。

本文采用数值模拟方法，通过添加边界约束项和半程反映点对Nelder-Mead 优化算法进行改进，构建的单纯形可以高效优选出带约束条件下产量最高的井位。该方法在均质储层部署一口井的算例中得到了验证，在非均质储层、多口井、规避地面特定区域中也能实现井位优选。

1 数学模型

原油产出是一个复杂过程，包括储层孔缝间的跨孔隙尺度间传质传压、油气水多相多组分运移、热流固化多物理场耦合以及解吸扩散渗流等多过程流动。非常规油气的产出则更为复杂。本文主要研究井位优选工作，故而简化原油渗流过程，假设储层为双孔介质。在基质孔隙中，流动规律满足达西渗流定律；在压裂裂隙中，流动满足裂隙流。

1.1 渗流控制方程

本文采用基质和裂缝耦合渗流模型。达西定律理论假设：当流体流过多孔介质时，流体的速度场由流体的压力梯度、黏度和流过路径决定，忽略重力作用，其表达式为

式中：u是达西流体速度；k是多孔介质渗透率；μ是流体动力黏度；∇是压力梯度算子；p是流体压力。

原油状态方程为

式中：ρ是流体密度；Cf为流体压缩系数；p为流体压力；下标“0”表示初始状态。

将式（1）代入连续方程，得到基质孔隙中流体流动的控制方程，为

式中：φ是基质孔隙度；Cp为岩石的压缩系数；Qm是流体的质量交换项。

在裂缝中，流体流动满足裂隙流，通过切向导数来计算沿内部边界的流量，以此表征模型内的嵌入裂缝，并与基质孔隙流量和压力耦合。达西定律的切向形式为

式中：qf是单位长度裂缝的体积流量；df是裂缝宽度；∇T表示裂缝切向的梯度算子。

裂隙的控制方程为

式中φf是人工裂缝的孔隙度。

为优选井位，本文使用累积产量作为评价指标，通过对井周处的法向渗流速度进行积分，得到日产量，再对日产量进行时间积分得到累积产量，计算公式为

式中：Q(x，y)是井位在（x，y）处的累积产量，t是时间，uT是井周处的法向渗流速度。

1.2 改进Nelder-Mead 优化算法

根据对优化目标函数是否求导，优化算法被分为梯度优化算法和非梯度优化算法。单纯形调优法是一种简单可靠的非梯度优化算法。在井位优选工作中，由于断层等构造的存在，往往会出现梯度无限大的情况，因此，无梯度优化算法更适用。1965 年Nelder 和Mead 对正则单纯形调优法进行了改进，使其在迭代计算中，出现的单纯形不一定是正则的，并且单纯形在计算中可以变大，也可以变小，同时改进后的单纯形调优法搜索成功率更高，收敛速度更快。但是该算法存在2 个缺点：1）Nelder-Mead 算法是无约束优化算法，无法在井位优选中避让不适宜布井的区域；2）当约束起作用的情况时，最坏点被形心x3另一侧点代替的机会将明显减小，最高点被压缩的次数会增多，甚至导致单纯形过多地收缩，影响收敛。因此，本文对Nelder-Mead 算法进行了改进：添加约束项并控制反映点的延伸速度。改进后的优化算法如下。

给定3 个初始点x0、x1、x2：

式中，n为维数，本文为二维模型，故n=2。设置反映系数a=1，收缩系数b=0.5，扩展系数c=2，紧缩系数d=0.5，并构建单纯形，为

以累计产量为目标函数Q，分别计算并比较单纯形H各点（井位）的函数值，按照目标函数由高到低对各点重新编号后，得到

此时，称x0为H最好顶点、x2为最坏点。判断x0是否满足截止条件，若是则其为最优井位，否则进行最坏点迭代替换，主要步骤如下。

1）反映。首先，求取H中去掉最坏顶点x2后，具有2 个顶点的单纯形H1（x0，x1）的重心，为

再求最坏顶点x2关于重心x1的反映点，如图1(a)所示。

图1 反映点计算方法Fig.1 Computing method of refraction point

式中α是反映系数。由于反映点可能出现在约束区（井位优选的避让区），因此，需要对该点进行约束处理。处理方法为：检验反映点是否在约束区，如果在，则将反映点替换为x2、x4连接线与约束区范围线的近交点；否则反映点成立，如图1(b)所示。

2）扩展。如果Q(x4)＞Q(x0)，方向（x4-x3）是使得目标函数值上升的有利方向，可在x4和x3连线的延长线上，求得扩展点，并同样检验约束区，为

式中c是扩展系数。如果Q(x5)＞Q(x0)，就用x5替换x2，构成新的单纯形H2（扩展单纯形），如图2 所示。

图2 扩展点计算方法Fig.2 Computing method of extension point

3）半程反映点。如果Q(x4)＜Q(x0)，但Q(x4)＞Q(x1)，方向（x4-x3）是使得目标函数值缓慢上升的有利方向，可在x4和x3之间的连线上，求得半程反映点，并同样检验避让约束区，如图3 所示，如果Q(x4′)＞Q(x1)，并用x4′替换x2，构建新的单纯形H3。

图3 半程反映点计算方法Fig.3 Computing method of half-way refraction point

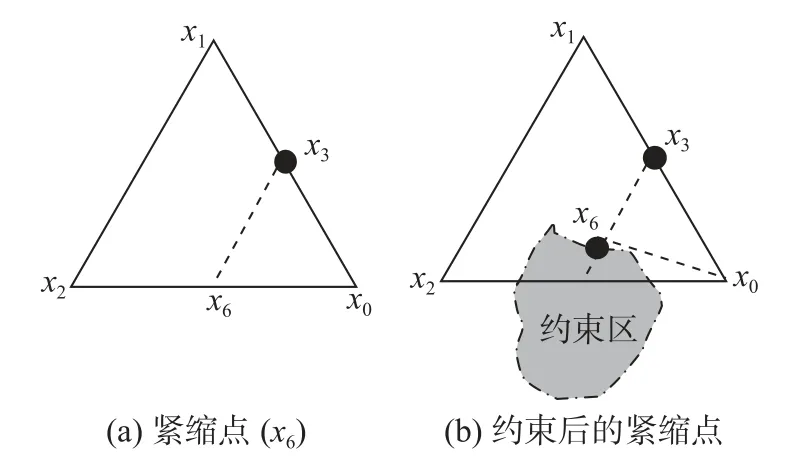
图4 紧缩点计算方法Fig.4 Computing method of contraction point

5）收缩。当Q(x6)≤Q(x2)时，为方便起见，将x4和x2之间目标函数值较大的点记为x2，另外一个记为x4，并在x2和x3的连线上靠近点x2处求一个收缩点x7，如图5 所示，并构成新的单纯形H4（收缩单纯形）。

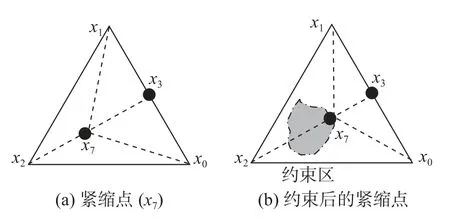
图5 收缩点计算方法Fig.5 Computing method of shrinkage point

在井位优选中，通过反映点、半程反映点和扩展点向低产能井位x2的反方向迭代，当反映点方向不利于增产时，通过紧缩点和收缩点向高产量井位x0的方向迭代。改进后的Nelder-Mead 优化算法流程如图6 所示。

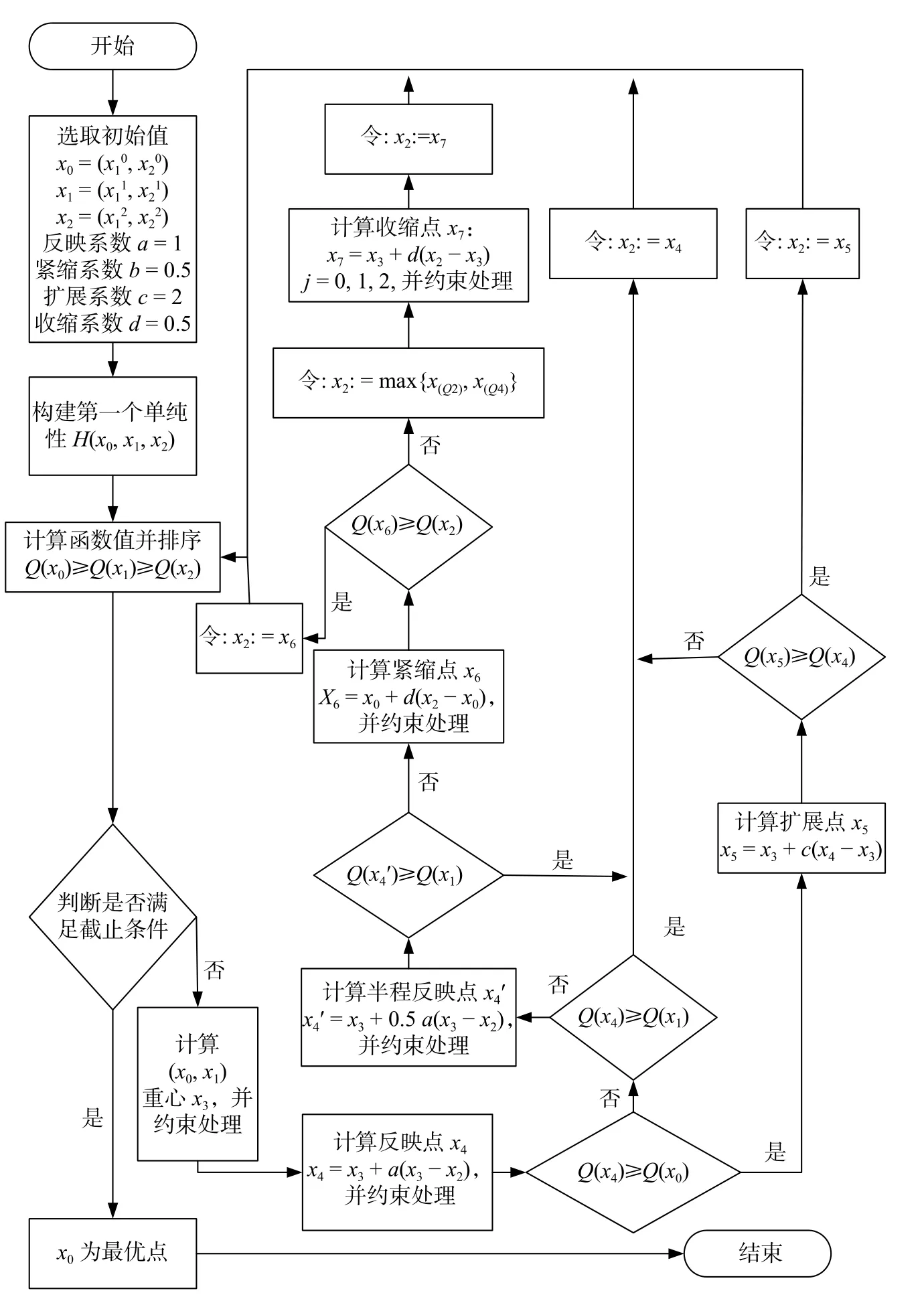
图6 基于改进Nelder-Mead 算法的井位优选方法流程图Fig.6 Flow diagram of well location optimization based on improved Nelder-Mead algorithm

2 模型验证

本文以累计产量为优化目标，通过改进Nelder-Mead 优化算法，逐步迭代出相同生产时间内累积产量最高的井位。为验证该算法的适用性、精度和迭代速度，设置60 m×60 m 的正方形理想均质油藏模型，井周围设置2 条裂隙，进行井位优选模型的实验，如图7 所示。模型几何和工况参数如表1 所示。从产量公式（6）可知，理想模型的最优井位应在储层的中心位置。

表1 模型参数Tab.1 Model parameter

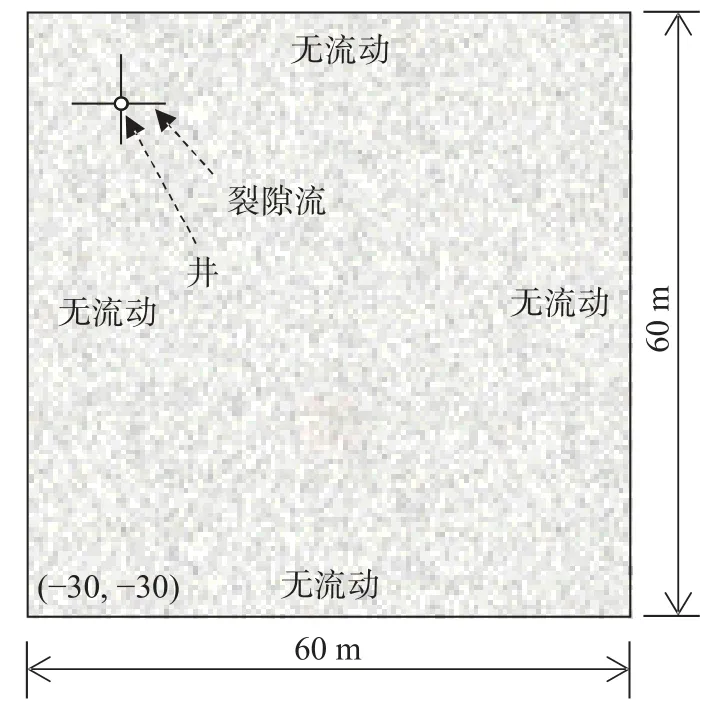
图7 理想模型示意图Fig.7 Diagram of ideal model

对该模型生产800 d 求解，由于油藏在整个油藏区均匀分布，所以最优井位应该在油藏区中心，坐标为（0 m，0 m）。迭代计算的井位坐标优选过程，如图8 所示。初始井位在（-20 m，20 m）处，迭代过程中，井位逐步优选到原点附近，最优计算结果为（-0.437 1 m，-0.384 1 m），这与预计结果一致。

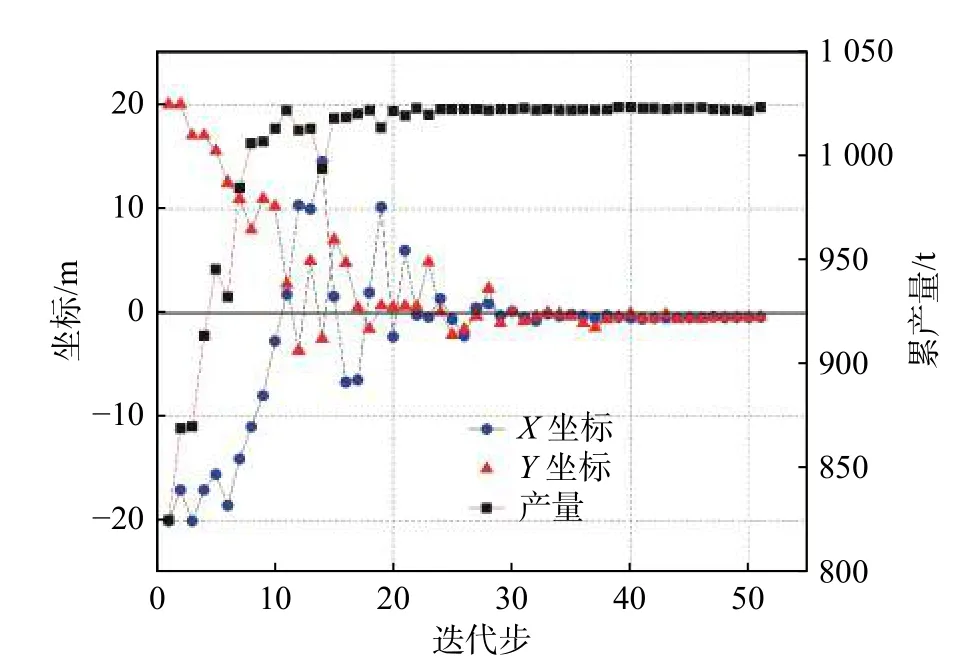
图8 理想模型迭代过程井位坐标曲线图Fig.8 Well location coordinate curve of ideal model

为评价计算结果，定义计算的最优井位到理想最优井位的距离，与油藏边界到理想最优井位的距离之比为误差，如公式（17）所示。本例的模型误差为1.372%，其中X、Y坐标的误差分别是1.457%和1.281%。其计算结果表明，该算法基本可以满足工程应用。

式中：ε、εx、εy分别是模型总误差、X方向误差和Y方向误差；Xi、Yi分别是井位X和Y坐标；Xboun、Yboun分别是X方向和Y方向的模型边界半长。

在优化工作中，COBYLA 算法是常用优化算法[32]，通过对目标函数进行抽样，构建和控制在移动置信区间内目标的线性近似。该方法收敛速度快，计算量小，被广泛使用。本文通过与COBYLA算法对比，来验证本文算法的精度。其误差对比结果如图9 所示，COBYLA 算法误差约为6.89%，本文算法误差为1.37%。

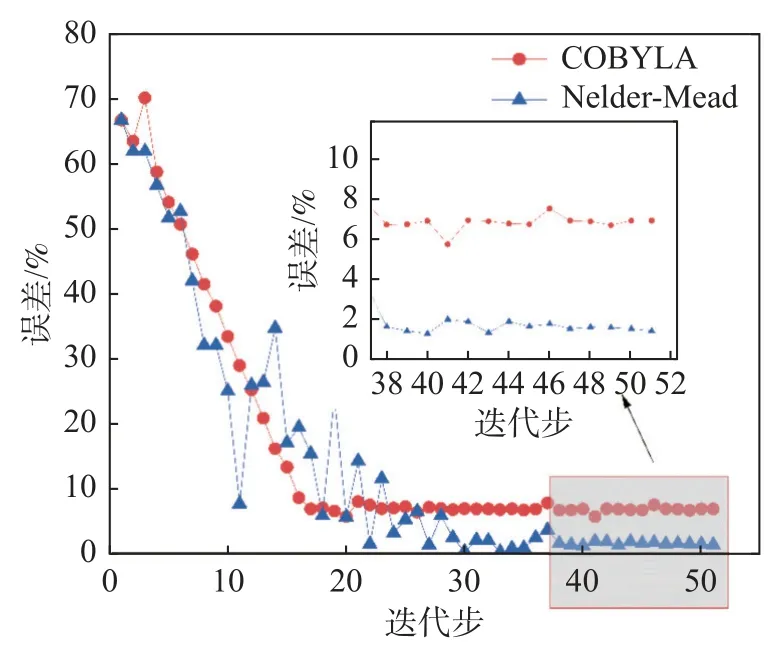
图9 算法误差对比图Fig.9 Algorithm error comparison chart

3 算例

在矿场选井位时，为更准确地优选出最佳井位以提高产量，需考虑储层非均质性、多口井部署、地面约束等情况。本章分别对渗透率非均质性、3 口井部署和避让特定区域3 种情况进行井位优选，以验证改进的Nelder-Mead 算法优选井位的适用性。

1）考虑渗透率非均质性井位优选算例。由于实际工程中，油气藏的渗透性在空间分布上差异较大，在上述模型的基础上，将油藏渗透率与空间坐标关联，重新计算最优井位。假设油藏空间某点的渗透率，与该点（x,y）到左下方角点的距离成正比，同时保证任一点的渗透率不小于30 mD，表达式如方程式（18），渗透率如图10(a)所示。模型其他参数仍然如表1 所示，非均质渗透率下的最优井位迭代计算过程如图10(b)所示，最优井位的坐标为（10.353,9.726），该点基本在副对角线上且偏向高渗区，在一定程度上说明了该模型是正确的、适用的。

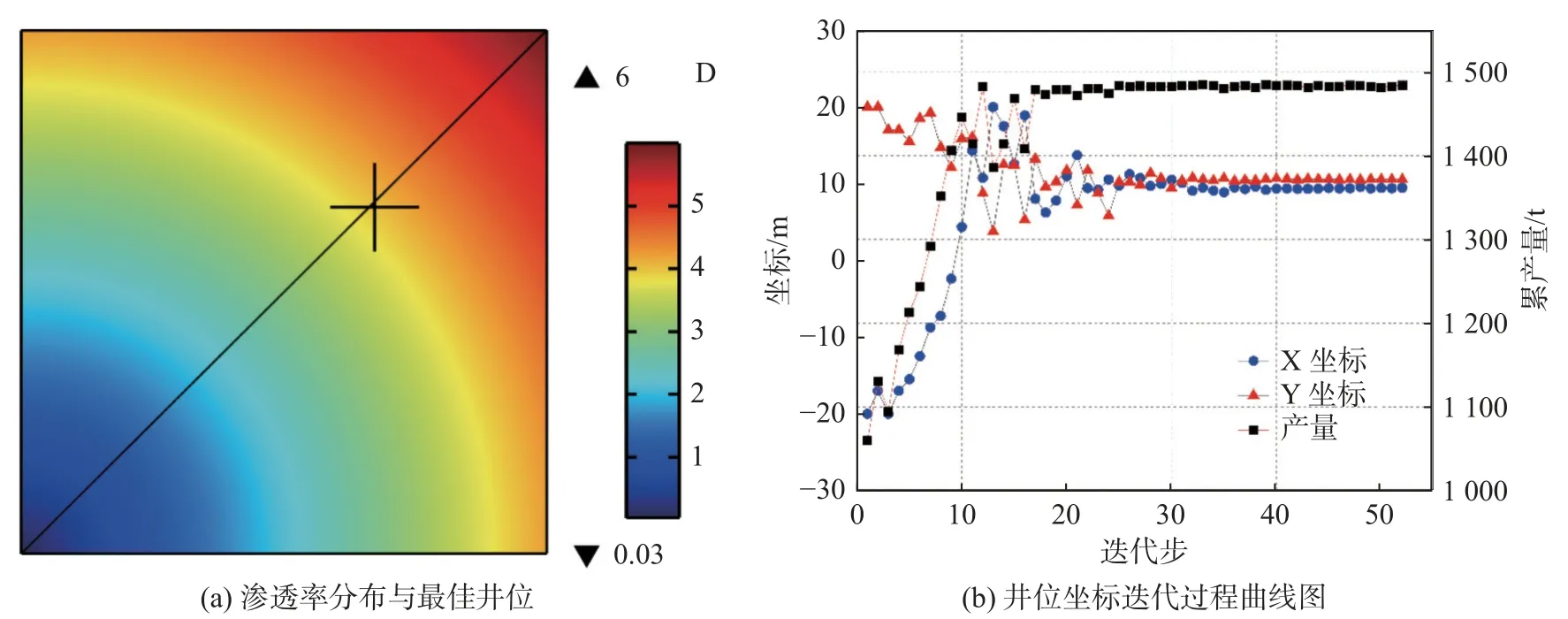
图10 渗透率非均质条件下的最佳井位与坐标迭代曲线图Fig.10 Optimal well location and coordinate iteration curve for heterogeneous permeability

式中（x0，y0）是空间左下角点位的坐标值。

2）3 口井井位优选算例。在油气田规模开发时，需部署多口井同时开采，此时应以当前开采工艺的总体产量为优化目标。部署3 口井进行井位优选，优选的最佳井位在开采800 d 后的压力分布如图11(a)所示，3 口井基本均匀分布在整个油藏区上。井位坐标迭代如图11(b)所示。本文算法在3 口井井位优化时，迭代80 步即可基本稳定收敛到结果，相对于1 口井的井位优选，约需要30 步迭代（图8），计算效率有所提高。

图11 部署3 口井时的最佳井位分布与坐标迭代曲线图Fig.11 Optimal well location and coordinate iteration curve for three wells

3）避让地面特定区域井位优选算例。在井位部署时，由于地面可能存在建筑，地形可能存在河流、沟壑等需要避让的区域，因此井位需要避开这些特定区域。在部署3 口井算例中，对优选到的C 井附近一个圆形区域进行避让运算，优选后的最佳井位如图12(a)所示。由于避让特定区域，3 口井的井位均发生了较大变化，其中原优选在避让区的井（C 井）调整到避让区外侧，但并非避让区外围边界。井位坐标迭代如图12(b)所示，迭代步数较无避让区时增加约30%，避让后3 口井的累产量没有明显下降。这说明当存在避让区时，本文算法依然可以优选到合适的井位。