基于相位相消法的消声降噪结构设计研究

杨悦华 李文婷 雷佳瑞 叶文旭 崔宇杰 谢文婷 唐一璠 高洁

(陕西师范大学物理学与信息技术学院 陕西 西安 710000)

多孔材料和微穿孔吸声体作为传统吸声解决方 案，根据经典的声学理论，通常具有与工作波长相当的结构厚度，这阻碍了它们在低频的潜在应用[1-2]，传统的吸声解决方案存在体积较大且受环境影响较大的缺点。近年来，基于声学超构表面调控声波目前已被广泛研究，且被证实具有非凡的调控能力[3]，更值得注意的是，压电材料本构方程决定其力学性质和电学性质具有耦合相关，相较于直接调控力学边界条件，电学边界的控制更加方便和高效[4]。因此，本文构建了一种基于相位相消法的超表面消声结构，即利用声波之间的相消干涉原理，使声场局部区域声能可以相互抵消，从而达到降低噪声的目的[5]。如图1所示，当入射声波和反射声波相位正好相差180°时，可以相互抵消。

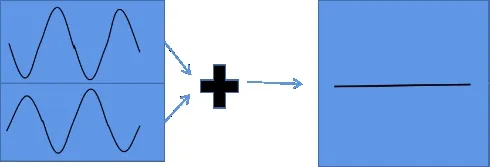
图1 相位相消法原理图

本文将压电陶瓷片粘贴在金属铜片上，压电复合状材料与外部电容器相连，并控制该结构的外接电路元件，通过改变外部电容器的容值，实现对反射声波相位的任意调控，当两个压电复合状材料耦合外接不同容值的电容时，可以实现该材料的消声性能[4-6]。由数值模拟结果表明：该结构两端加以特定数值的电容时可以实现噪声的抑制，同时利用B&K阻抗管对该结构进行实验测试，验证结构在特定频段具有很好的消声降噪功能。

1 仿真模型的建立

1.1 模型单元结构设计

本文提出的声学超表面单元结构由三部分组成：第一部分为并排放置的两片由铜片和薄片状压电陶瓷耦合形成的压电复合薄层状材料，铜板和薄片状压电陶瓷片的直径分别为D1=26.8 mm和D2=18.6 mm，厚度为H1=0.2 mm和D2=0.2 mm；压电陶瓷极化方向为其轴线方向；第二部分为放置在压电复合薄层状材料下方的管道，下方管道长为20 mm，开口半径与压电薄片半径相等，其上端开口，下端及周围以硬边界封闭；第三部分为两个可调电容分别与两个压电复合薄层状材料构成的无源闭合回路，可调电容两端的连接点分别固定于铜片和压电陶瓷片，如图2所示。

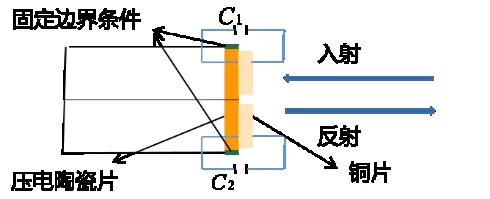
图2 耦合结构模型

1.2 模块选择与材料设置

本文使用有限元仿真软件进行数值模拟，利用压力声学、固体力学以及电路模块，铜片的周围设置为固定边界条件，使用背景压力场作为入射声源并设置为1 Pa，将面探针放置在超表面附近来探测反射系数和反射相位。

管道中填充密度为1.29 kg/m3，声速为343×（1+0.02×i） m/s的空气，i是虚数单位；铜片密度为8 960 kg/m3，杨氏模量为120×109×（1+0.05×i）Pa，泊松比为0.34；压电陶瓷片密度为7 500 kg/m3。

1.3 基本原理的定量描述

由于该结构工作时工作波长远大于该结构背腔的尺寸，因此可建立集总参数模型。背腔舒张和压缩的空气在腔体内相当于弹簧模型，而背腔上部空气相当于附在弹簧上的重物，此时在入射声波的激励下，背腔的工作就像弹簧的受迫振动，这时声阻抗可以表示为

声波的阻力Ra=Rm/Sn2；声波的质量Ma=Mm/Sn2；背腔的容积为Ca=CmSn2；Sn=πa2是背腔的横截面积。此时该系统的声振动方程可以写为

式（2）中：U为容积，P为声压压强。当背腔上部空气开始振动时，进入腔体的空气体积和增加的压强可表示为δV=U/(jω)，δP=ρ0U/(jωV0)，其中ρ0=1.29 kg/m3为空气密度，V0为c0=343×(1+0.02×i)m/s空气中的声速，考虑背腔上部阻尼的影响后，声阻抗表达式可以修改为[7-8]

2 数值模拟分析

2.1 共振频率的测量

在仿真模拟中的压力声学模块下，发射频率范围在3 260～3 560 Hz 的入射平面波，对所设计的结构进行扫频操作，计算得到反射系数随声波频率的变化曲线以及声波相位随频率的变化曲线。由图3（a）可知，随频率值增加，反射系数基本保持1不变，说明反射声波能量强度与入射声波能量强度基本相等，入射声波到达超表面后能量基本没有衰减。如图3（b）显示，声波相位随频率值的增大而增大，但相位在f=3 410 Hz时产生突变，表明3 410 Hz为共振频率。

图3 声波反射系数和反射相位随频率的变化曲线

2.2 可调电容值的确定

在仿真模拟中的压力声学模块下，将图3 得到的共振频率作为入射声波的频率，计算得到声波相位随电容值大小变化的曲线图，如图4所示，在图中找到相位为0°和180°时对应的电容值，分别为-8×10-9F 和-5.2×10-9F。

图4 声波反射相位随电容值变化曲线

2.3 相位相消法的模拟结果

本文设计使用相同的结构，通过改变结构的附加电容，达到声波吸收的效果。利用图4 得到的相位为0°和180°对应的电容值，分别将0°对应的电容值-8×10-9F 和180°对应的电容值-5.2×10-9F 输入，绘制得到声压图。如图5（a）所示，输入0°对应的电容值时，超表面上方的声压强度两端最强，中间最弱。如图5（b）所示，输入180°对应的电容值时，超表面上方的声压强度两端最弱，中间最强。这表明：在入射平面波的频率与结构的共振频率相等的条件下，当入射平面波撞击超表面时，两个结构都具有强响应，但反射声波反相。因此，通过改变结构的附加电容，这两个相同的结构耦合实现了组合谐振模式，它们以180°的相位差显著振动，使反射声波相位相反，而相位相反的声波叠加之后的效果为0，表现为入射声波在超表面附近被吸收，反射声波效果为0，如图5（c）所示，相位相反的声波相互叠加的效果为0，达到了声波吸收的效果。

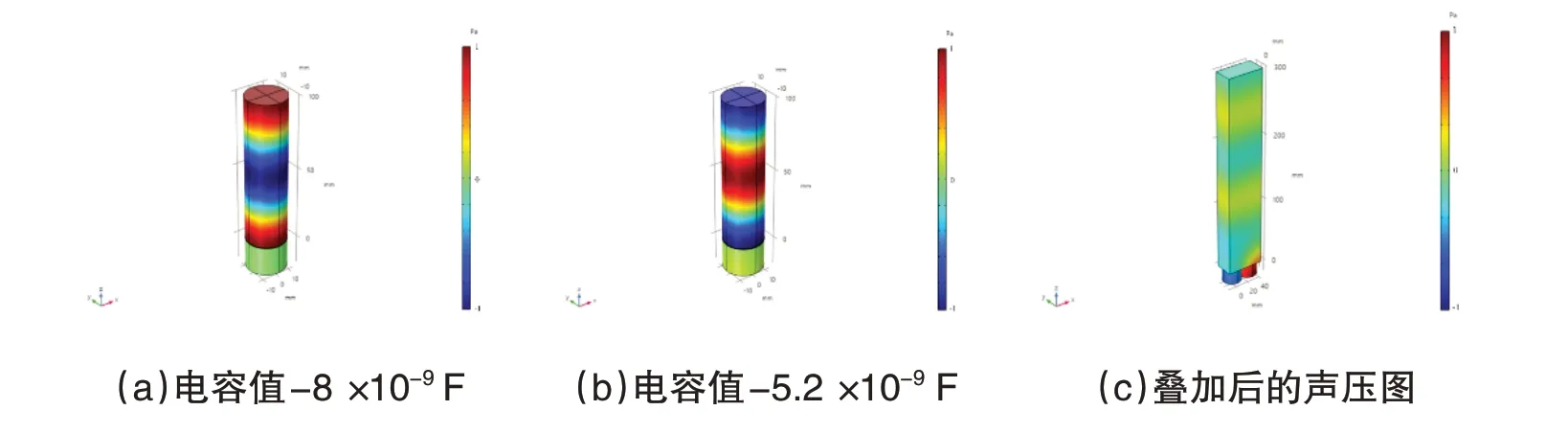
图5 调节电容消声示意图

3 实验验证与结果分析

3.1 吸声单元结构设计

本文实验所用的声学超表面单元结构由三部分组成：第一部分为周期排列的两片——铜片和薄片状压电陶瓷片通过粘贴形成的压电复合薄层状材料，铜板和薄片状压电陶瓷片的直径分别为D1=26.8 mm和D2=18.6 mm，厚度为H1=0.2 mm和H2=0.2 mm；第二部分为高度为15 mm，开口半径略大于铜片的管道，其上端开口，下端以及周围为硬边界封闭；第三部分为焊接点分别在铜片和压电陶瓷片的两根导线与可调电容构成的无源闭合回路。具体如图6、图7所示。

图6 消声结构实物图

图7 可调电容实物连接图

3.2 实验过程与步骤

为测量铜片和压电陶瓷薄片所组成的压电复合薄层状材料的共振频率，实验中使用pulse软件利用B&K阻抗管双传声道法进行测量，如图8所示。第一步，打开测量软件点击analyses填写通道信息为对应序号；第二步，对传声器进行校准；第三步，将传声道1 选作参考点，由数值仿真结果可知该结构的理论共振频率为3 810 Hz，因此实验中将pulse 软件的频率扫描范围设为2 000～5 000 Hz，测量结束后得到声波反射相位随频率的变化曲线，如图9所示。从图像可知3 408 Hz位置时相位出现突变，该突变相位所对应的频率即为该结构的共振频率。

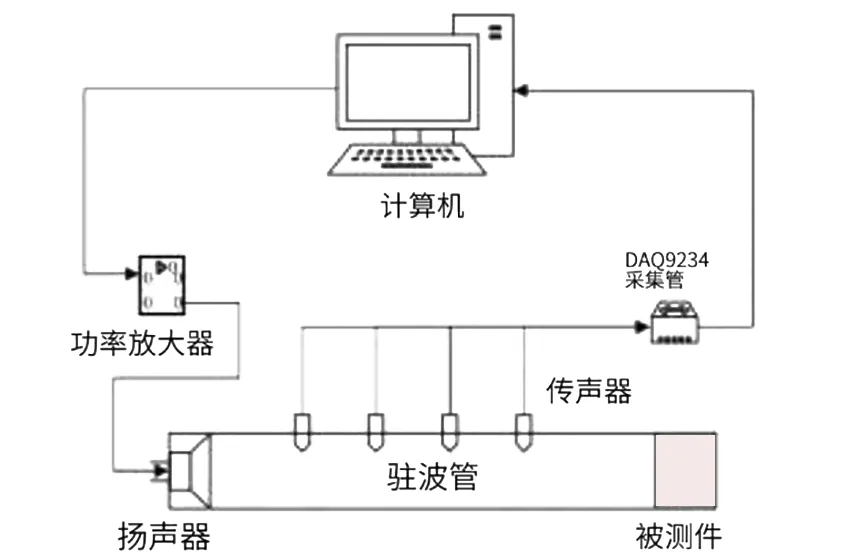
图8 仪器测试示意图

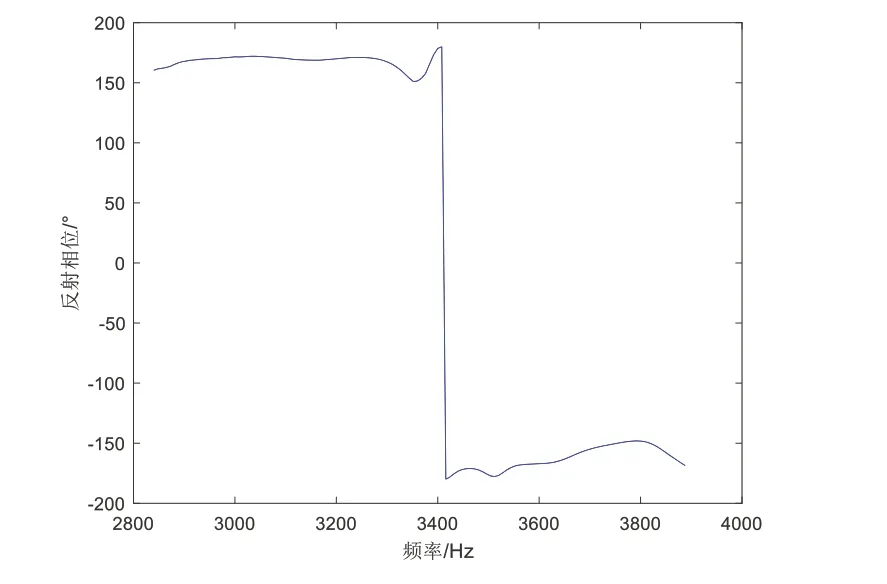
图9 结构共振频率

为拓展该结构的应用频率范围[9-10]，改变该结构的参数将其共振频率向频率较低处过渡，实现抑制低频噪声的功能。通过多次优化计算，确定铜板和薄片状压电陶瓷片的直径分别为D1=26.8 mm和D2=2 mm，厚度为H1=0.04 mm 和D2=1.5 mm，模拟过程如3.2 小节中的实验过程与步骤所示，得到声波反射相位随频率的变化曲线，如图10 所示，优化结构在470 Hz 位置时相位出现突变，该突变相位所对应的频率即为该结构的共振频率。该结构的降噪频段大大降低，因此通过对结构的背板和压电片进行设计就可实现降噪频段的任意可调，如果将这些结构进行组合叠加即可实现宽频段的降噪结果[11]。

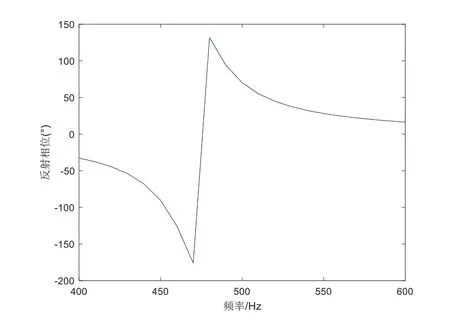
图10 声波反射相位随频率的变化曲线

4 结语

本文将压电复合状材料与外部电容器相连，并利用数值模拟控制该结构的外接电路元件，通过改变外部电容器的容值实现对反射声波相位的任意调控，当两个压电复合状材料耦合外接不同容值的电容时，实现该结构的消声性能。对模型数值的结果和实验得到数据进行分析，该结构的共振频率模拟数值和实验数据高度吻合，且通过优化设计结构参数，可使该结构的共振频率调至470 Hz 的较低频段，利用这种方法可实现消声频段的任意调控，最终实现宽频段结构简单、成本低廉的消声降噪设计。