均布荷载下两端固支深梁的解析解

梅甫良

(嘉兴学院 建筑工程学院，浙江嘉兴314001)

梁的平面应力问题是弹性力学中的一个非常经典的问题，也是实际工程经常遇到的问题.Timoshenko 和Gooder研究了各向同性悬臂梁的拉伸、剪切、纯弯曲、横弯曲以及两端简支各向同性梁在均布荷载或其他荷载作用下的弯曲问题.[1]Lekhnitskii研究了两端简支各向异性梁在均布或线性分布荷载作用下的弯曲问题.[2]Ahmed 等给出了两端固支深梁的有限差分解.[3]陈玉骥获得了单跨超静定梁在均布荷载作用下的弹性力学解.[4]樊友景等获得了均布荷载作用下两端固支梁的弹性力学解.[5]张伟等给出了集中荷载作用下两端固支梁的弹性力学解.[6]王晓琴等导出了均布荷载作用下悬臂梁的弹性力学解.[7]上述弹性力学解，都是采用了固支边原始位移条件下的不同简化(1)边界上中点固定不动，即该点不能移动，水平线不能转动.所获得的半逆解析解，这是由于应力函数是空间坐标的多项式函数，所以它无法满足固支边原始位移条件.因此，用多项式应力函数求解时都是采用简化的固支边位移条件.

最近，文献[8]建议的固支边位移条件简化处理为固支边中点2个纵横方向的位移u、v以及∂u/∂y(或∂v/∂x)为零，据此条件所获得的远离固支边各点处纵横向位移和纵向正应力的精度较高，而固支边附近各点的计算精度却不是很高.尔后，戴瑛等对文献[8]建议的固支边位移简化条件进行了改进，提出一种改进型固支边位移条件，仍然令固支边中点2个纵横方向的位移u、v为零，但不以固支边中点∂u/∂y(或∂v/∂x)为零作为固支边位移条件，而是改为以固支边顶点纵向位移u为零，这种改进型固支边位移条件所获得的受均布荷载作用下，两端固支短梁的解析解与其有限差分解符合得较好，[3]特别是所获得的固支边附近各点处纵向正应力解析解与有限差分解之间的相对误差，比起以文献[8]等建议的固支边位移简化条件所获得的固支边附近各点纵向正应力解析解与有限差分解的相对误差要来得小.[9]可是，运用戴瑛等建议的改进型固支边位移条件来求解悬臂深梁的平面应力问题时发现，虽然所获得的应力解析解与有限差分解比较符合，但其横向位移解析解与有限差分解的差距是比较大的.综上所见，固支边位移条件的简化改进与两端固支梁固支边的位移实际约束情况是比较一致的，但它与一边固支、另一边自由悬臂梁固支边的位移实际约束情况是有差距的.[9]

图1 两端固定均布荷载深梁

本文在前人研究成果的基础上，提出了一种新型固支边位移简化条件，即令固支边的纵向位移u、横向位移v以及纵向位移u对横向坐标z的一阶导数，沿高度方向进行积分后都为零；以均布荷载作用下两端固支梁平面应力问题为例，用本文提出的固支边位移简化条件和半逆解法推导出其应力和位移解析解.为了探讨本文建议的固支边位移简化条件的正确性和可靠性，给出了文献[8]的两个固支边位移简化条件与文献[9]的1个固支边位移简化条件所得的解析解和以固支边原始位移条件所取得的有限元解，将本文所得的应力位移解析解分别与现有其他3种不同简化处理的固支边位移条件所获得的解析解和原始固支边位移条件所取得的有限元解进行了对比研究.

1 问题描述与基本方程

考虑厚度为单位1、长度为l和高度为h的两端固定矩形截面深梁，其上表面受均布荷载q的作用，而下表面不受力，如图1所示.

在不计体力的情况下，其平衡微分方程、几何方程和应力应变方程分别为：

(1)

式(1)中，σx、σz和τzx是应力分量，εx、εz和γzx是应变分量，u和w是位移分量，E和μ分别是材料的弹性模量和泊松比.

应力边界条件为：

(2)

位移边界条件为

u=0，w=0 (x=0) 和 (x=l)

(3)

2 半逆解法

应力分量可用应力函数U表示：

(4)

式(4)中应力函数U已自动满足重调和方程.

本文采用Ding H J[8]等建议的7项五次多项式应力函数U：

U=a(z5/5-x2z3)+bxz3+cz3+dz2+ex2z+fxz+gx2

(5)

式(5)中a、b、c、d、e、f、g是7个待定系数.

将式(5)代入式(4)，可得应力分量的表达式为：

(6)

将式(6)代入式(1)中的应力应变方程，再代入式(1)中的几何方程和应力应变方程，可得位移分量的表达式：

(7)

式(7)中，u0，v0和ω为积分常数.

应力函数式(5)中的7个待定系数和位移表达式(7)中的3个积分常数，可由应力边界条件式(2)和位移边界条件式(3)确定.采用上述多项式解法，难以满足固支边位移条件式(3).因此，本文采用简化的固支边界条件.

对固支边界条件，文献[8]等建议的位移简化条件如下：

(8)

或者

(9)

文献[9]又提出了一种新的简化固支边界条件如下：

(10)

由式(10)可见，文献[9]用固支边顶点纵向位移为零的条件代替固支边中点∂w/∂x=0或∂u/∂z=0的条件.

在现有文献成果的基础上，本文对固支边提出了一种新的简化固支边界条件如下：

(11)

最后，利用式(11)和式(2)，即可确定式(5)中的7个待定系数和式(7)中的3个积分常数，具体如下：

(12)

将求得的上述待定系数和积分常数代入应力分量式(6)和位移分量式(7)，就可以求得梁内任一点处的应力分量和位移分量.

由上述4种不同固支边简化条件式(8)、(9)、(10)和(11)所确定的10个待定系数中发生差异的3个系数c、ω和v0，示于表1中.

表1 4种不同固支边简化条件下受影响待定系数的比较

3 算例分析

以梁的长高比l/h=2、均布荷载q=60×106N/m2、弹性模量E=200Gpa、泊松比μ=0.3为例,采用文献[8]建议的重调和应力函数(4)并结合4种不同固支边简化条件式(8)～式(11)分别获得了其应力和位移解析解,还利用ANSYS10.0软件获得了其应力位移有限元数值解.在本文的有限元法中,梁的跨度方向为200等分,高度方向为100等分,左、右固支边上所有节点水平和竖向位移均设为零.所有计算结果示于表2和图2～图8中.

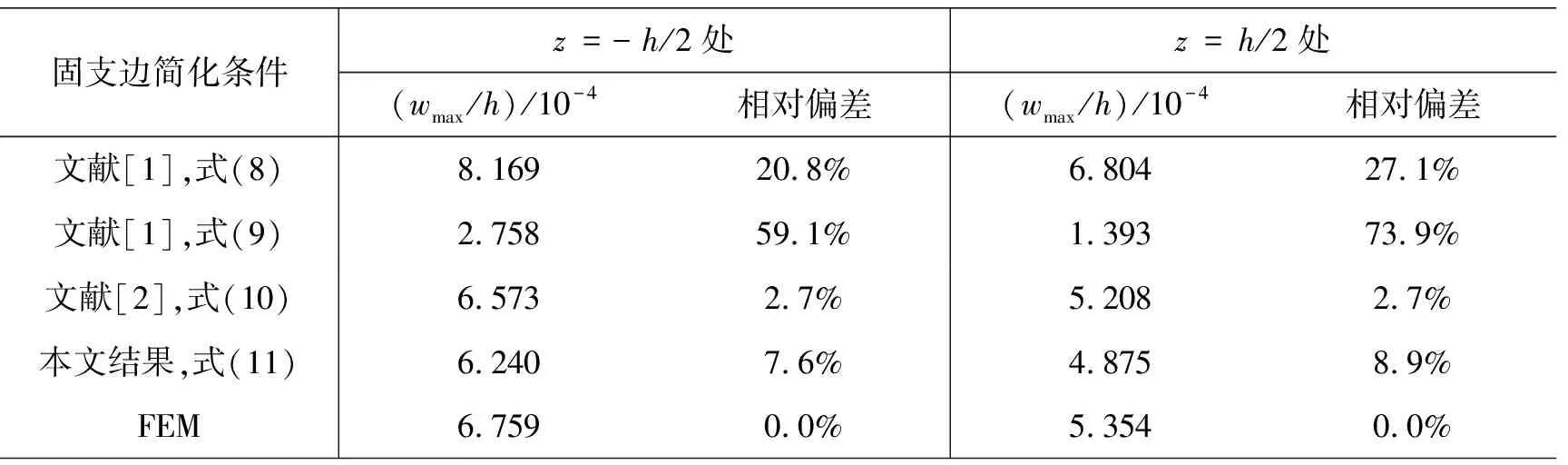
表2 梁上、下边最大挠度值的比较

图2和图3分别给出了不同简化固支边界条件时，在z=-h/2和z=h/2沿长度方向的挠度分布，表2列出了不同简化固支边界条件下，梁上、下边最大挠度值及其相对偏差.由图2、图3和表2可见，按文献[8]建议的简化固支边界条件式(8)下的梁上、下边最大挠度与有限元计算结果的相对偏差分别为20.8%和27.1%，而按文献[8]建议的简化固支边界条件式(9)下的梁上、下边最大挠度值与有限元计算结果的相对偏差分别为59.1%和73.9%.文献[9]提出的简化固支边界条件式(10)下的梁上、下边最大挠度值与有限元计算结果的相对偏差都很小，只有2.7%.运用本文提出的固支边简化条件式(11)所导出的梁上、下边最大挠度值与有限元计算结果的相对偏差也不大，分别为7.6%和8.9%.可见，采用本文简化固支边界条件式(11)所得的位移精度是相当高的.

图2 z=-h/2处挠度分布图3 z=h/2处挠度分布图4 x/l=0.5处应力分量σx分布图5 x/l=0.5处应力分量σz分布图6 x/l=0.05处应力分量σx分布图7 x/l=0.05处应力分量σz分布

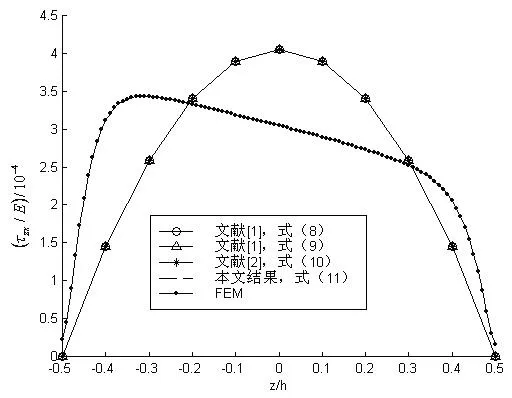
图8 x/l=0.05处应力分量τzx分布

图4和图5分别给出了4种不同简化固支边界条件下，梁中截面(x/l=0.5)上的应力分量σx和σz解析曲线和有限元数值计算曲线.由图5可见，这4条解析曲线是完全重合的，而与σz有限元数值计算曲线几乎重合.由图4可见，本文的σx解析曲线与文献[9]建议的固支边简化条件下所得的σx解析曲线是完全重合的，且与σx有限元数值计算曲线十分接近.然而，按文献[8]采用的固支边简化条件式(8)或式(9)所得的σx解析曲线偏离σx有限元数值计算曲线较大，尤其是在梁顶、梁底附近.由此可以证明，本文建议的固支边简化条件式(11)比文献[8]的固支边简化条件式(8)或式(9)更加接近固支边的实际约束情况，因此是可靠的，也是合理的.

图6、图7和图8分别给出了四种不同固支边简化条件下的固支边附近截面(x/l=0.05)上的应力分量σx、σz和τzx解析曲线和有限元数值计算曲线.由图6可见，本文的σx解析曲线与文献[9]等建议的固支边简化条件(10)所得的σx解析曲线是完全重合的，介于由文献[8]等推荐的固支边简化条件式(8)和式(9)所得的两条σx解析曲线解之间.本文的σx解析曲线与有限元数值计算曲线之间存在一定的偏差，但是其偏差很小.由图7和图8可见，本文的σz、τxz解析曲线与文献[8-9]推荐的固支边简化条件式(8～11)所得的σz、τxz解析曲线是完全重合的；在梁顶边和底边的计算上，本文的σz、τxz解析值与相应的有限元数值计算值重合；在其他点上，本文的σz、τxz解析值与有限元数值计算值存在一定的差别.这是由于本文简化固支边界条件式(11)与固支边实际约束之间的差异造成的.由此可见，基于各种不同固支边简化条件所得的固支边附近的各应力分量值的计算精度，会受到不同固支边简化条件的影响，但从图6可见，本文建议的固支边简化条件对固支边附近的主要应力分量σx的计算精度影响是比较小的，是可以接受的.

4 结论

本文提出了一种新的固支边简化条件，采用半逆解法导出了均布荷载作用下两端固支深梁平面应力问题的应力和位移解析表达式.同将本文的应力和位移解析解与其他3种固支边简化条件所得的应力和位移解析解及有限元数值解进行了比较，结论发现，该简化固支边界条件能够较真实刻画固支边实际约束情况，是合理的、可靠的；不论是在固支边附近还是其他区域的应力和位移精度，受本文固支边约束简化条件的影响都是比较小的.