最小二乘法在连续梁施工监控中的运用

代 涛

（武汉光谷建设投资有限公司，湖北 武汉 430200）

在大跨度桥梁的施工控制过程中，在状态预测中对设计参数的识别和调整是一项重要的工作[1]。对设计参数的识别和调整采用的方法有Kalman滤波法、灰色理论法和最小二乘法等[2]。最小二乘法是一种传统的优化方法，理论体系和计算方法比较完善，在桥梁施工控制中主要用于设计参数的识别、修正和状态预测[3-5]。但如何保证设计参数的估计值收敛于实际值是最小二乘法应用的关键，因此需要进一步开展理论研究和数值计算。文章以新建铁路广州枢纽东北货车外绕线（40+64+60） m预应力混凝土连续梁桥施工控制为例，将监控数据、参数误差作为设计参数并应用最小二乘法进行识别和调整，实现施工过程的流线型控制。

1 最小二乘法的基本概述

最小二乘法定义为未知量的最可能值使实践值与计算值的差的平方乘以测量精度后所求得的和最小[6]。该方法也适用控制系统的参数估计领域，在稳态数学模型的回归分析方面广泛应用。在桥梁施工监控过程中，对比监测的实际数据与理论数据，运用最小二乘法分析偏差及其修正偏差，可以预测后续施工可能出现的变形状态。

2 连续梁桥施工控制特点

悬臂施工阶段的连续梁桥是静定结构，合龙过程中若不施加额外压重，成桥后的内力状态通常符合设计要求。因此，施工控制要确保主梁的线形可控。连续梁是节段施工，如果已施工梁段出现误差，误差将一直存在，只能通过未施工节段调整弥补。

针对未施工梁段，可以通过调整立模标高调整已施工梁段的残余误差。如果残余误差较大，需要调整几个梁段才能完成调整。悬臂浇筑连续梁桥的标高控制特点是已完成梁段的误差无法调整，而未完成的梁段的立模标高只与模拟计算有关，不受已完成梁段的误差影响。

在连续梁施工控制中，参数估计及对计算模型的修正具有重要的作用。目前，线性控制中有限元模拟可以用于预测梁体的线形，帮助确定施工过程中需要调整的控制点和参数。通过对已施工梁段和未施工梁段的模拟，可以预测梁体的线形误差，采取相应的调整措施。可以利用最小二乘法拟合变形曲线，调整模型参数，更好地匹配实际情况，为结构行为提供更准确估计。

桥梁线性控制基本原理如图1所示。

3 最小二乘法在桥梁施工监控中的应用

最小二乘法在桥梁施工监控中的应用是通过拟合监测数据提供准确的数据分析和结果。可以用于分析桥梁结构的位移、应力或挠度等数据，帮助监测人员评估结构的健康状况和性能。最小二乘法通过最小化残差平方和找到最佳拟合曲线或平面，能够准确地描述监测数据的趋势和变化，具有对异常值的鲁棒性，适用线性和非线性问题。

最小二乘法在桥梁施工监控中的应用包括分析和拟合桥梁结构的位移、应力或挠度数据。通过应用最小二乘法，可以从监测数据中提取关键信息，评估结构的安全性和稳定性，及时采取必要的措施进行维修或调整。

数据分析和拟合：最小二乘法可用于分析桥梁监测数据，如位移、挠度、应力等，拟合出最佳的曲线或平面描述数据的变化趋势。通过拟合数据可获得准确的结构变化信息和未来的变化趋势。

结构参数估计：最小二乘法可以用于估计桥梁结构的重要参数，如刚度、强度等。通过应用最小二乘法，可以基于监测数据反推出结构参数的值，能够更好地了解结构的性能和特性。

桥梁位移监测：最小二乘法可以用于分析和拟合桥梁的位移数据，评估结构的变形情况。通过对位移数据进行分析，可以检测到桥梁的变形趋势、结构的稳定性和变形的程度。

桥梁振动监测：最小二乘法可以用于分析和拟合桥梁的振动数据，评估结构的振动特性。通过对振动数据进行分析，可以确定桥梁的固有频率、振动模态和结构的动力响应。

桥梁应力监测：最小二乘法可以用于分析和拟合桥梁的应力数据，评估结构的受力情况。通过对应力数据进行分析，可以确定桥梁各个部位的应力分布，评估结构的强度和承载能力。

桥梁结构健康监测：最小二乘法可以对桥梁结构的健康状况进行评估。通过分析和拟合监测数据，可以检测到结构的异常变化、损伤或破坏，提供早期预警，以便采取适当的维修和保养措施。

异常检测和预警：最小二乘法可以用于检测和识别异常的监测数据点。当监测数据偏离预期模式时，最小二乘法可以帮助确定异常点，提供预警信号，以便及时采取适当的措施。

最小二乘法在桥梁施工监控中的应用需要结合合适的传感器和数据采集系统，确保高质量地监测数据。此外，数据预处理、异常值检测和误差分析等技术也是应用最小二乘法的重要步骤，可以提高数据的可靠性和准确性。通过对监测数据的分析和拟合，可以及时发现问题，采取必要的措施，确保桥梁的安全运行和可靠性。

4 最小二乘法应用的基本步骤

运用最小二乘法对连续梁的累计变形量与理论累计变形量的参数进行识别，得到拟合函数，根据拟合函数预测下一阶段的理论累计变形量与实际累计变形量。

先拟合函数y=a+bx；将已经辨识的数据代入拟合函数中，建立超定线性方程组；依据最小二乘估计法求出函数的最小值，对最小值求偏导，得出a、b值与拟合函数；依据得出的拟合函数预测下一阶段的理论累计变形量与实际累计变形量。

根据以上步骤运用最小二乘法推导拟合函数，假设对含有m组中n个参数进行最优估计（m≥n）。

依据最小二乘估计法：

令Yi=yi-ai，有：

对S(a，b)求偏导得：

5 最小二乘法在连续梁中应用

选取前6个施工节段（实测值与理论值）为计算节段，得出拟合方程，预测下一节段的实测值与理论值。

施工现场实测1#～6#块的累计变形量：

根据最小二乘估计法得出：

对最小值求偏导：

故拟合函数为：

由拟合方程得到第7#块、第8#块的累计变形量，y7=-23.53，y8=-24.73。

拟合方程预测累计变形量与理论累计变形量对比如表1所示。

表1 拟合方程预测累计变形量与理论累计变形量对比

由表1可知，拟合方程预测第7#块、第8#块累计变形值理论计算值差距较小，最大误差1.17 mm。表明用最小二乘法对连续梁桥施工监控计算的方法具有可行性。通过修正混凝土密度参数，调整混凝土、后续施工中的各阶段预拱度值调整误差。

修正后的拟合函数：

修正后由拟合方程得到第7#块、第8#块累计变形量，y7=-24.6，y8=-25.8。

修正预测的累计变形量与理论的累计变形量对比如表2所示。

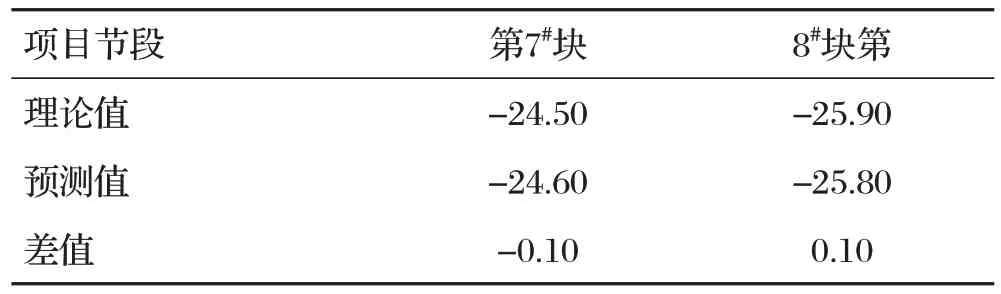
表2 修正预测累计变形量与理论累计变形量对比

由表2可知，修正后拟合方程预测第7#块、第8#块的累计变形值更接近于理论计算值，最大误差为0.1 mm。表明调整混凝土能够有效修正混凝土密度参数，调整后续施工中的各阶段预拱度值等措施，能够控制连续梁体的流线型。

在梁体上安装一组传感器，用于测量梁体的垂直位移。传感器每隔一段时间记录一次位移数据，并将数据存储在数据库中。在施工过程中，当梁体的位移超过预定的阈值时，工程团队会收到警报通知，表明可能存在梁体的异常变形，需要立即采取行动。对梁体进行检查，根据监测结果做出决策，如增加支撑、调整施工方案或进行结构加固等。

通过最小二乘法的实时监测和分析，能够及时发现和解决梁体变形的问题，确保施工的安全性。在连续梁施工监控中应用最小二乘法，能够评估和控制梁体的变形行为。

6 结语

采用最小二乘法对大跨径混凝土连续梁桥进行后续的预测分析具有可行性，对流线型的控制效果较好。

通过采取修正混凝土密度参数及调整各阶段预拱度等措施能够有效减小误差，对流线型具有一定控制效果。

最小二乘法可用于连续梁结构健康监测，通过分析监测数据的变化趋势检测结构的异常变形或破坏，可以及时发现问题，采取必要的维修和保养措施，确保连续梁的结构安全性和可靠性。