基于改进NSGA-Ⅱ算法的医疗垃圾转运站选址优化研究
2023-11-21郭政杰
郭政杰 孙 涛*
(内蒙古科技大学信息工程学院,内蒙古 包头 014010)
1 医疗垃圾转运相关研究
医疗垃圾转运站的选址是一种综合决策问题。肖鸿等[1]设计出新颖的医疗垃圾的回收模式与流程,通过运用Lingo软件进行计算,对回收的节点进行选址决策。类似的问题还有城市生活垃圾转运站的选址问题。衡婷等[2]运用模糊德尔菲法,对城市生活垃圾分类转运站的选址体系进行选择并提出相应的建议。周浩等[3]为了解决交通线路建设物资的物流节点选址问题,建立以运输成本和时间惩罚成本之和为目标函数的数学模型,在经典的P-median选址模型基础上,采用线积分取代离散点表示现状需求,证明目标函数在给定区间内为凸函数,利用二次插值和黄金分割法相结合的算法对模型进行求解。Kargar等[4]提出一种多目标线性规划模型,最小化运输处理医疗垃圾的费用、运输风险以及存放在医院未收集的医疗垃圾这三个目标。潘马超等[5]为了促进垃圾分类政策的实施,科学、合理地在居民生活小区设置垃圾分类站,建立选址模型和成本模型对垃圾分类站建设运营成本及居民满意度负效应成本进行求解,通过对比K-means聚类算法和Cmeans聚类算法验证了K-menas聚类算法的优越性。Yao等[6]针对医疗垃圾的处置开发了一种双层平衡优化模型,在减小医疗垃圾可能对公众造成危害风险的同时,可以降低运输和处理医疗垃圾的费用。Joneghani等[7]针对医疗废物管理中的选址分配问题,提出了一种不确定性条件下的多目标混合整数线性规划模型,此模型设计了一个网络,为医疗废弃物的储存、净化、回收、焚烧和处置提供方案。
2 基于保护弱势群体的医疗垃圾转运站选址模型
2.1 P-median选址模型
P-median选址问题是一个经典的设施选址问题[8],研究如何选择P个服务站使得需求点和服务站之间的距离与需求量的乘积之和最小。在本文的Pmedian模型中,服务站即医疗垃圾转运站,需求点即为城市中的各个医院。每个需求点的需求量即为每家医院每日产生且需要转运的医疗垃圾量。本模型中假设医院之间以及医院与医疗垃圾转运站之间的距离均为直线距离。模型约束条件主要有两类:一类是医疗垃圾转运站与幼儿园、养老院以及污水处理厂等地址的最小距离约束;另一类是医疗垃圾转运站与各个医院的最大距离约束。
P-median模型的目标是使医疗垃圾转运站与医院之间的距离和各个医院每日产生的医疗垃圾量的乘积之和最小,最小化医疗垃圾的转运成本。模型构建公式为:
式中:Z——P-median模型目标函数;i——医疗垃圾转运站;I——医疗垃圾转运站集合;j——医院;J——医院集合;o——养老场所;O——养老场所集合;p——污水处理厂;P——污水处理厂集合;k——幼儿园;K——幼儿园集合;wij——i转运站对j医院的医疗垃圾转运量(kg);dij——i转运站与j医院之间的距离(km);dio——医疗垃圾转运站i与养老场所o的距离(km);dip——医疗垃圾转运站i与污水处理厂p之间的距离(km);dik——医疗垃圾转运站i到幼儿园k的安全缓冲距离;dh——医疗垃圾转运站与敏感区域的安全距离,设为0.8 km;dz——医疗垃圾转运站和医院之间的最大距离,此处设为5 km;Xij——0~1变量,i服务于j则Xij为1,否则为0。
2.2 选址风险模型
医疗垃圾中存在很多传染性的病毒和细菌,因此医疗垃圾转运站周围一定的半径范围内不能存在人员密集的场所或绿地、水系,应尽可能远离这些场所。本研究中把这些场所称为敏感地址。本模型假设医疗垃圾转运站对周围的危害风险主要集中在横向的平面区域,不考虑纵向的危害风险。模型的约束条件为医疗垃圾转运站与周围敏感地址的距离约束,模型目标是在医疗垃圾转运站服务区域内,最大化医疗垃圾转运站与其周围敏感地址的距离。模型构建公式为:
式中:S——医疗垃圾转运站与人员密集场所以及水源、绿地等地址距离的目标函数;q——具体的人员密集场所以及水源、绿地等地址;Q——具体的人员密集场所以及水源、绿地等地址的集合;diq——医疗垃圾转运站i与敏感地址q的距离(km);dm——医疗垃圾转运站与敏感地址的最大距离,此处设为5 km;Xiq——0~1变量,i方圆2 km内存在q则Xiq为1,否则为0。
2.3 多目标规划模型
本模型是对P-median选址和选址风险两个模型进行同步规划,约束条件与以上两个模型的约束条件相同。此模型旨在同时兼顾医疗垃圾转运站的转运成本最小化以及医疗垃圾转运站对周边敏感地址可能造成的危害风险最小化这两个优化目标。
Multi Objective为P-median和选址风险模型的多目标规划目标函数,多目标规划模型公式为:
式中:dab——地球上任意两点a与b之间平面距离;R——地球的半径,6 371 km;na——a处纬度弧度;nb——b处纬度弧度;ma——a处经度弧度;mb——b处经度弧度;majd——a处经度;mbjd——b处经度;nawd——a处纬度;nbwd——b处纬度。
3 实验的设计与实现
3.1 实验数据说明
本文收集了包头市72家大中型公立医院的地理信息坐标数据和病床数,138家包头市的主要幼儿园的地理信息坐标数据、50家包头市养老院和养老公寓机构的地理信息坐标数据以及3家污水处理厂以及相关在建工程的地理信息坐标数据。预估72家医院每日需要转运的医疗垃圾量时,根据医院的级别以及病床数来进行估算[9],全国性的三甲医院一般单位病床每日产生0.74 kg医疗垃圾,省级重点医院一般单位病床每日产生0.6 kg医疗垃圾,地市级别的医院一般单位病床每日产生0.48 kg医疗垃圾。
3.2 实验流程
实验流程分为三个步骤。第一步是对城市医院进行K-means聚类计算实现区域划分;第二步是运用Lingo软件对P-median模型进行求解;第三步是运用改进后的NSGA-Ⅱ算法进行多目标规划求解,实现多目标规划模型目标函数值的最小化。
3.2.1 K-means聚类计算
(1)K值的设定。
本文采用K-means聚类算法对城市医院进行初步聚类,将距离相近的医院分为同一个类别,对不同的类别再次进行聚类计算,得出最终的细分区域的个数。细分区域的个数即为转运站的个数,即每一个医疗垃圾转运站负责特定的几家医院的医疗废弃物的回收。因此,本实验首先采用K-means聚类算法对包头市72家主要的大中型公立医院进行分类,运用聚类算法前需要初步确定聚类的个数,实验采用“手肘法”得出最优的聚类个数为3,因此将72家医院分为3个类别。其中“手肘法”的核心指标是误差平方和(SSE),计算公式为:
式中:Ci——第i个簇;P——Ci中的样本点;mi——Ci的质心(Ci中所有样本的均值);SSE——所有样本的聚类误差,代表了聚类的优劣。
随着K增大,样本划分会更精细,每个簇的聚合程度会逐渐提高,SSE就会逐渐变小。K值增大到一定程度时,再增加K值得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减。
“手肘法”实验结果如图1所示。
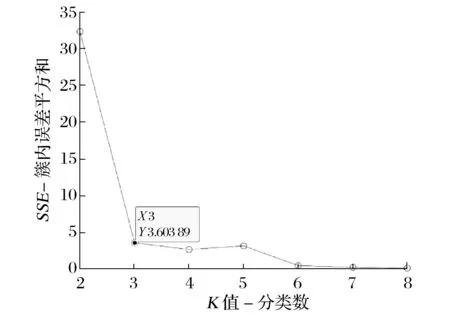
图1 “手肘法”实验结果
由图1可知,当K≤3时,误差平方和迅速减小;当K≥3时,误差平方和曲线变得平缓,此时“手肘法”认为K=3是最优值。
(2)两次聚类计算与分析。
确定k=3后,对医院地理数据进行K-means聚类计算,完成聚类计算后,将72家医院根据地理位置分为三个类别即A、B、C三个区域,由于每个区域内部医院的分布密度有较大差异,因此分别对A、B、C三个区域再次进行K-means聚类分析实验。此步骤实验采用Matlab2021b中的数据聚类工具箱,求出各区域内部最优的分类个数。A区域聚类实验结果如图2所示。
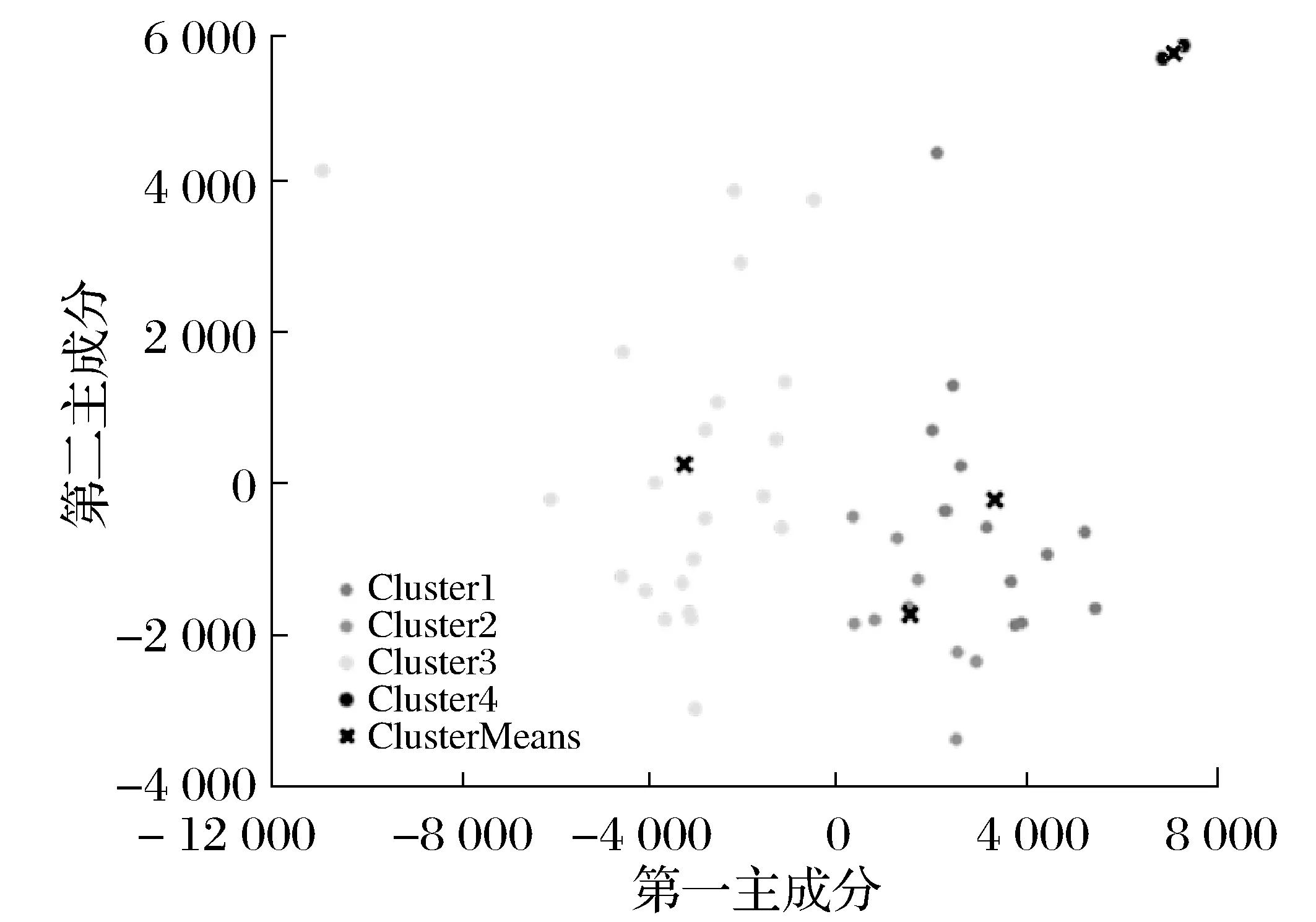
图2 A区域K-means聚类分析实验
A区域的最优分类数是4个,以此方法求出B区域的最优分类数是2个,C区域的最优分类数1个。因此,在A、B、C三个区域分别选择4、2、1个医疗垃圾转运站地址,其中,A区域的4个细分区域命名为A1、A2、A3、A4,B区域的2个细分区域命名为B1、B2,C区域的细分区域为C1。其中A1、A2、A3、A4区域分别包含18、2、21、5家医院;B1、B2区域分别包含14、9家医院;C1区域共包含3家医院。
3.2.2 运用Lingo对A1区域P-中位模型求解
本文在进行多目标规划之前,会先使用交互式的线性和通用优化求解器(Lingo)对各个细分区域进行P-median模型计算,计算出在本文P-median模型的约束条件下的最优解即潜在医疗垃圾转运站的地理坐标。在此坐标周围半径2 km内,搜索出所有的人口密集场所和敏感地址的地理坐标,为下一步的选址风险模型做准备。以A1区域为例,A1区域包含18家医院、27家幼儿园、7家养老院。通过Lingo对A1区域进行P-median模型计算,潜在选址经度109.791 5、纬度40.644 4,P-中位模型最小模板函数值13 482.95。设点(109.791 5,40.644 4)为潜在选址的坐标A1q,在A1q周围半径2 km内又搜索出6个人口密集场所和敏感地址。
由于A1区域有18家医院和6个敏感地址,因此A1区域的多目标规划模型需要同时优化24个目标,其中18个为P-median模型的优化目标,旨在使该区域医疗垃圾转运站同每家医院的距离与每家医院每日需要转运的医疗垃圾量的乘积之和最小。6个为选址风险的优化目标,旨在使该区域的医疗垃圾转运站与6个敏感地址的距离之和最小。
地理位置坐标和名称如表1所示。

表1 A1q周围2 km内敏感地址坐标
3.2.3 多目标规划模型设计
传统的NSGA-Ⅱ算法在初始化种群时采用随机生成,随机产生意味着不确定,因此在解决多目标非线性规划问题时,容易陷入局部最优或者种群空间分配不均匀的问题。本实验改进了传统的NSGA-Ⅱ算法,采用传统的NSGA-Ⅱ算法计算出多目标规划函数的解集,从中挑选出目标函数值低的解;再次运行NSGA-Ⅱ算法,但在生成第一代子群时,不再随机产生初始种群集合,而是采用第一步NSGA-Ⅱ算法计算并挑选出来的解集即“佳点”种群作为初始种群,然后进行计算求解。改进后的NSGA-Ⅱ算法如图3所示。

图3 改进后的NSGA-Ⅱ算法流程
鉴于选址风险模型是以K-means聚类算法计算得出的每个细分区域为单独的对象,对其进行风险模型计算,使各细分区域潜在的医疗垃圾转运站的备选地址坐标与敏感地址的坐标在约束条件下保持尽可能远的距离。本实验中的选址风险模型包含于多目标规划模型中,因此选址风险模型不再单独论述。经过改进后的NSGA-Ⅱ算法计算出来的解集中的P-median模型的目标函数值和选址风险模型目标函数值均有降低,表明改进过的NSGA-Ⅱ算法求出的解集更优。改进前后的A1区域P-median目标函数值计算结果如图4所示。
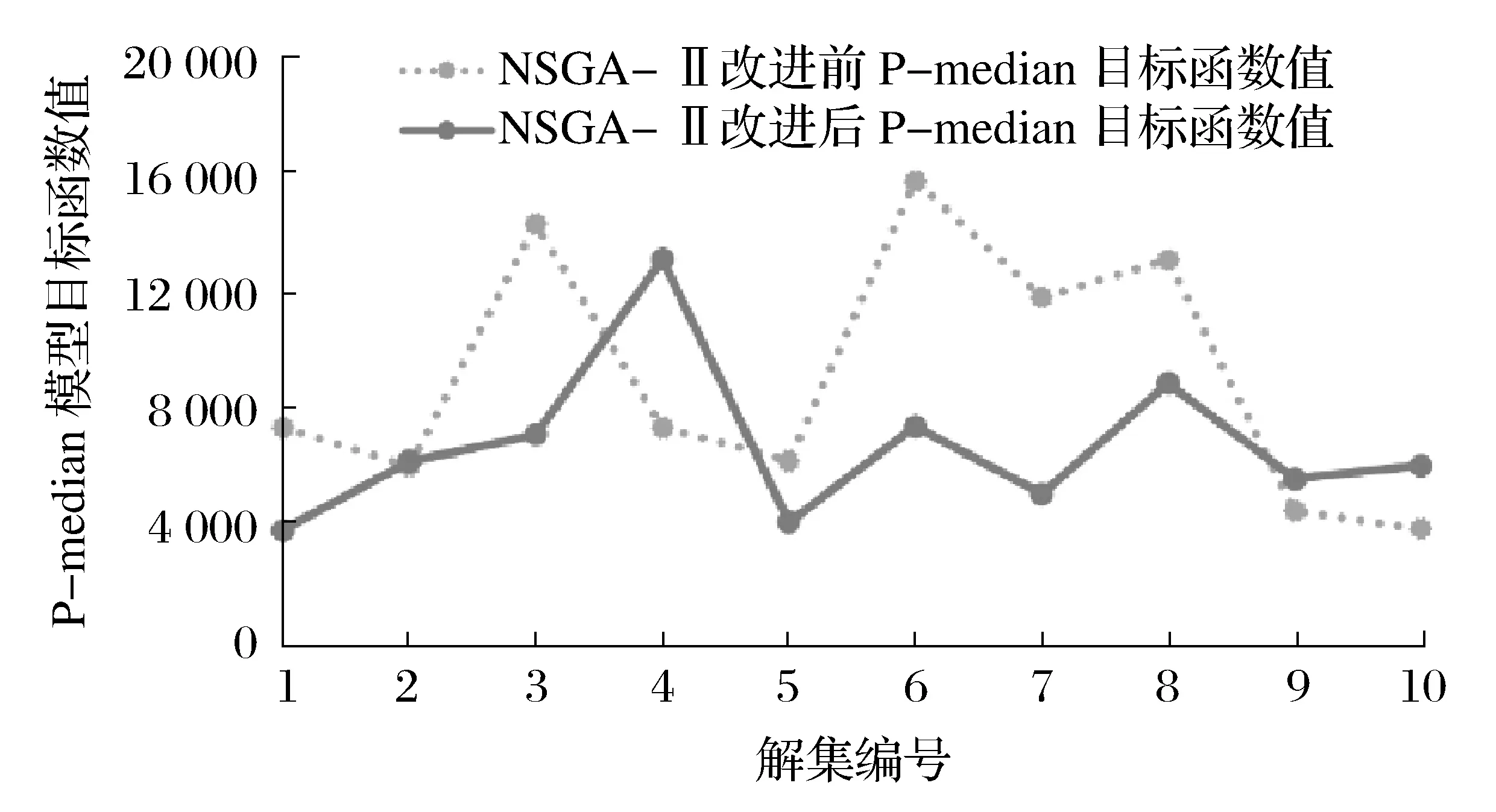
图4 NSGA-Ⅱ改进前后P-median目标函数值对比
经过改进后的NSGA-Ⅱ算法计算出来的选址风险目标函数值也有明显下降,结果如图5所示。
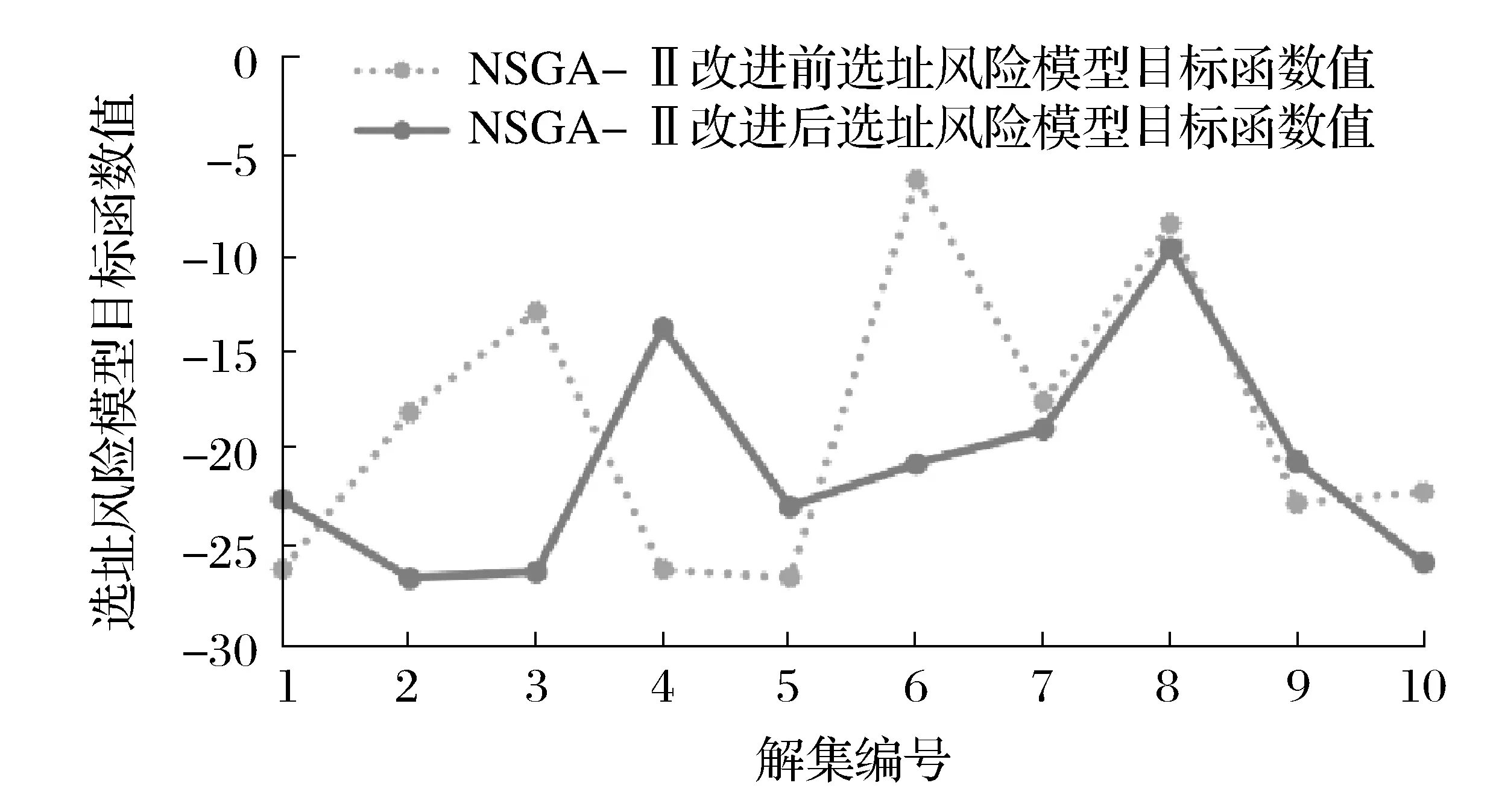
图5 NSGA-Ⅱ改进前后选址风险模型目标函数值对比
通过改进NSGA-Ⅱ算法,本文中多目标规划中的P-median模型和选址风险模型的目标函数值都取得了明显的下降,其中P-median的目标函数值平均下降了11.44%,选址风险模型的目标函数值平均下降了33.39%。改进后的解集优于改进前的解集。
4 实验结果评价
本文采用CRITIC权重法(客观赋权法)对解集中的选址坐标进行赋权评价,最终选出最优的解,即选出区域内最优的医疗垃圾转运站的地址坐标。
采用SPSSPRO在线数据分析软件进行CRITIC权重法的计算与分析,SPSSPRO是一款集专业统计方法与数据算法于一体的在线式数据处理与分析平台。本文对最终选址的评价设定了四个指标,分别为转运站备选地址与交通干道的距离、转运站备选地址与人口聚集区的距离、转运站备选地址与医疗垃圾处理中心的距离、转运站备选地址下风向居民点的数量。医疗垃圾处理中心在本文中指的是包头市的医疗垃圾处置点包头市绿源公司;医疗垃圾转运站备选地址的下风向在本研究中假设是指东南风向。相关指标数据如表2所示。

表2 A1区域备选地址评价数据
运用SPSSPRO在线数据分析软件进行CRITIC权重法的计算与分析,分析过程中对医疗垃圾转运站的备选地址与医疗垃圾处理中心的距离以及此备选地址下风向的居民点的数量,两个指标进行负向化处理。指标负向化指的是值越大越劣,越小越优。备选地址下的居民点数量越少越优,备选地址距离医疗垃圾处理中心的距离越小越优。A1区域备选地址评价指数权重如表3所示。

表3 A1区域备选地址评价指数权重
根据表3的权重计算备选地址的最终得分,编号1~10对应权分别为2.35、2.36、2.38、2.38、2.48、2.39、2.39、2.37、3.19、2.59。
第9号备选地址的得分值最高,为3.196 0,因此9号备选地址为A1区域最终的备选地址,地理坐标为(109.755 046,40.638 082),根据本文的研究思路和实验方法及评价体系,求出所有区域最终的医疗垃圾中转站的地址,结果如表4所示。

表4 所有区域医疗垃圾转运站的最终选址坐标
5 结语
本研究在考虑对弱势群体保护的基础上,首先采用K-means聚类算法对城市的医院进行分区,确定各个区域的医疗垃圾转运站的数量,采用改进后的NSGA-Ⅱ算法对P-median模型和选址风险模型进行多目标规划,降低了模型的目标函数值,降低医疗垃圾转运站对周围人口造成危害的风险,降低了医疗垃圾的转运成本。最后采用CRITIC权重法对医疗垃圾转运站的备选地址进行赋权计算,求出最优医疗垃圾转运站选址的地理坐标。
