股票收益率能反映三阶矩信息吗?①——基于我国股票市场的实证研究

王 鹏,梁鑫垚

(西南财经大学中国金融研究院,成都 611130)

0 引 言

1952年,Harry Markowitz在JournalofFinance期刊上发表了Portfolio Selection一文.该论文明确地定义了投资收益和投资风险的概念,并分别用资产收益的一阶矩(均值)和二阶矩(方差)进行度量,这一方法及其奠定的“均值-方差”分析框架,成为后续诸多经典金融理论和金融工具发展的基石.受此影响,Sharpe[1]和Lintner[2]等学者先后提出了资产定价的一般均衡理论——资本资产定价模型(Capital Asset Pricing Model,CAPM模型).后来的研究者又在此基础上发展出了三因子[3]、四因子[4]和五因子[5]等模型,极大地丰富了资产定价领域的研究成果.

然而,就在“均值-方差”分析框架成为现代金融学理论发展基石后的很长一段时间里,Markowitz[6]在论文最后指出的一个重要问题却没有得到足够的关注:即当投资者的效用函数中不仅包括资产收益的一阶矩(均值)和二阶矩(方差),还包括三阶矩(偏度)信息时,即使是“经过精密计算的公平交易”,只考虑前两阶矩的投资者也无法做出准确而合理的选择,因此应该基于三阶矩等其它信息对“均值-方差”分析框架做进一步完善.在Markowitz[6]之后,Levy[7]和Samuelson[8]都曾指出:二次偏好无法描述投资者偏好的全貌,投资者的期望效用依赖于资产收益分布的所有阶矩,因此在构建投资组合时,资产收益的高阶矩是不容忽视的.需要指出的是,对于四阶矩以上的收益分布矩,由于很难确定其明确的经济学含义,所以目前绝大多数金融学文献中的“高阶矩”都是指三阶矩和四阶矩.又因为四阶矩所蕴含的部分极端波动信息被二阶矩所包含[9],所以三阶矩就成为了高阶矩研究的重中之重.

国外学者在三阶矩资产定价方面的研究起步较早,其中Kraus和Litzenberger[10,11]以不同形式将偏度引入CAPM模型,并发展出了三阶矩CAPM模型,这是在资产定价中较早考虑三阶矩信息的两项重要研究.此后,包括Chen等[12]、Boyer等[13]以及Anthony和Richard[14]在内的一系列研究都证明:偏度在资产定价中发挥着重要作用.值得一提的是,基于个股信息的偏度不仅可以预测个股收益,还可以预测市场表现,例如Jondeau等[15]的研究发现:当月个股偏度的市值加权平均数,对下月的市场收益有显著预测作用.

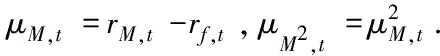
和异质性偏度,见1.1.2节～1.1.3节.

近年来,部分学者也对我国股票市场的三阶矩定价问题展开了若干讨论.例如,王金安和陈浪南[22]将流动性风险引入三阶矩资本资产定价模型,最终发现该模型在我国股票市场上有良好的解释能力.与之类似,陈国进等[23]将灾难风险和风险形成引入含高阶矩的资本资产定价模型,结果发现该模型能更广泛地解释中国金融市场的典型事实.郑振龙等[24]则在互换合约的统一框架下,采用无模型方法提取方差风险价格和偏度风险价格,并发现二者无法被市值因子(SMB)、价值因子(HML)、动量因子(MOM)和部分宏观变量所解释.关于三阶矩在我国股票市场的定价效应,郑振龙等[25]使用横截面回归的方法提取预期特质偏度,并发现预期特质偏度和预期收益率之间存在显著的负相关关系.史代敏等[26]基于NAGARCHSK模型推算中国股市收益率的条件高阶矩序列,并建立引入高阶矩风险的收益-风险时变四因子状态空间模型,最终发现条件偏度在出现极端金融危机和未出现极端金融危机的环境下,对投资收益存在不同方向的冲击.陈坚和张轶凡[27]则利用高频数据构建中国股市的已实现偏度,结果发现已实现偏度对中国股市有显著的预测能力.这些重要的研究成果对于深刻认识和把握我国股票市场的高阶矩定价效应具有积极作用.

不过,在对我国股票市场三阶矩定价效应的研究中,还存在诸多亟待改进之处:1)在度量偏度因子时,现有研究仅使用股票市场的交易信息,没有考虑上市公司的特征信息尤其是财务特征信息.但实际上,上市公司的特征信息对于度量偏度因子非常重要.举例来说,在市场大幅波动时,大市值的股票通常会表现出较强的稳定性,这意味着上市公司的市值会影响股票收益与市场波动之间的关系,即系统性偏度.如果上市公司在一段时期内由小公司成长为大公司,在预测未来偏度时,滞后的偏度反映的仍然是小公司的特征信息,那么预测结果必定存在较大的偏差.此时,引入市值作为控制变量将有助于提升预测精度.2)现有关于偏度定价效应的研究没有明确地将偏度区分为系统性偏度、异质性偏度和总体偏度,且这些研究所提及的偏度,几乎全部是指异质性偏度或总体偏度.对于系统性偏度,只有部分学者检验了三阶矩CAPM模型在我国股票市场的适用性[22,23],且没有学者对高次项系数的经济学含义做出明确定义,也没有学者将其视作独立的定价因子进行实证研究.因此,将偏度区分为系统性偏度、异质性偏度和总体偏度,并分别检验其定价效应是十分必要的.3)现有研究普遍围绕三阶矩CAPM模型来展开,还没有学者将偏度作为独立的定价因子引入三因子模型、四因子模型和五因子模型并检验其定价效应.由于三因子模型、四因子模型和五因子模型在我国股票市场的有效性已经被很多学者证实[28-30],因此这一处理会影响实证结果的稳健性.检验偏度因子在三因子模型、四因子模型和五因子模型中的定价效应,将使得实证结果更加可靠.

针对现有研究的不足,本研究的创新点和研究特色主要体现在:

第一,本研究同时使用股票市场的交易信息和上市公司的特征信息来预测未来偏度,以克服现有方法在预测能力方面的不足.如前所述,上市公司的特征信息对于预测未来偏度有重要的补充作用,因此在对未来偏度展开预测时,应该综合考虑股票市场的交易信息和上市公司的特征信息.具体操作上,将结合股票市场的交易信息和上市公司的特征信息,构建前瞻(3)这里的“前瞻”是指基于第t期的信息预测得到第(t+1)期的偏度.系统性偏度(predictive systematic skewness,PSS)因子、前瞻异质性偏度(predictive idiosyncratic skewness,PIS)因子和前瞻总体偏度(predictive total skewness,PTS)因子.

与此同时,本研究在实证技术设计上结合了我国股票市场的特点,对实证过程做了以下针对性调整:1)由于我国股票市场的波动性较大,本研究将通过在回归中设定滚动时间窗口来提升回归系数的时变性,使其充分反映我国股票市场的当前特征.2)部分国外学者在实证研究中不使用个股变量的真实值,而是使用个股变量的当期排位数(4)当期排位数是指上市公司某变量的数值在当期所有上市公司中的排位百分比.[31].然而,我国股票市场的发展时间较短,有相当数量的股票于近期才上市交易,这导致在不同时期,上市公司的行业分布存在较大差异.此外,部分早期特别是后来“被借壳”的上市公司在经历兼并重组以后,业务实质在时间上存在不连续性,其特征变量的当期排位数在时间上存在明显跳跃.因此在实证研究中直接采用个股变量的真实值,而不采用当期排位数.

第二,系统性偏度、异质性偏度和总体偏度的经济学含义存在显著差异,但关于我国股票市场的现有研究并没有明确地对其进行定义和区分,且几乎所有研究都是针对异质性偏度或总体偏度.对于系统性偏度,只有部分学者检验了三阶矩CAPM模型在我国股票市场的适用性,且没有学者对高次项系数的经济学含义做出明确定义,也没有学者将其视作独立的定价因子进行实证研究.因此,本研究将三者作为独立的定价因子,并分别对其在我国股票市场的定价效应进行实证检验,提升现有研究框架的完整性.

第三,如前所述,CAPM、三因子模型、四因子模型和五因子模型在我国股票市场的有效性已经被很多学者证实.然而,关于三阶矩定价效应的现有研究中,只有部分学者检验了三阶矩CAPM模型在我国股票市场的适用性,还没有研究将偏度因子同时引入CAPM、三因子模型、四因子模型和五因子模型.本研究认为这一处理会影响实证结果的稳健性,因此本研究不仅将偏度因子引入CAPM模型,也将偏度因子引入三因子模型、四因子模型和五因子模型.

第四,与隐含偏度和已实现偏度相比,本研究构建的偏度因子在数据可得性和运算便捷性方面更具优势.隐含偏度和已实现偏度被普遍认为是比传统偏度更好的测度方法,不过隐含偏度的计算需要使用期权数据,而中国目前还没有个股期权,因此无法获得个股的隐含偏度;已实现偏度则需要使用高频数据,对运算设备的要求更高.相比之下,本研究构建的三个偏度因子仍然基于低频历史数据,在数据可得性和运算便捷性方面更具优势.与此同时,在预测过程中引入反映上市公司特征信息的变量,一定程度上也可以弥补我国股票市场在有效性方面的不足.

1 前瞻偏度因子的构建

三阶矩定价效应检验的第一步(也是关键一步)是构建恰当的偏度因子.如前所述,现有研究对于偏度因子的构建主要基于股票市场的交易信息,而在预测未来偏度时,上市公司的一些自身特征又确实会影响预测精度.因此,借鉴Langlois[32]的方法来构建前瞻偏度因子.1.1节将重点介绍前瞻系统性偏度(PSS)因子、前瞻异质性偏度(PIS)因子和前瞻总体偏度(PTS)因子的构建过程;1.2节对本研究使用的数据样本进行说明,同时对主要的定价因子做描述性统计,并比较引入和不引入上市公司特征信息对偏度预测的影响,为后文的有效性检验奠定基础.

1.1 前瞻偏度因子的计算方法

1.1.1 系统性偏度及PSS因子的构建

本研究使用一种系统性偏度的经典度量方法,即从三阶矩CAPM模型出发

Et-1[ri,t-rf,t]=γM,tCovt-1(ri,t,rM,t)+

(1)

将上市公司的特征信息引入系统性偏度的预测过程,并基于Cosi,t来构建前瞻系统性偏度(PSS)因子.该过程主要包含以下四个步骤.

步骤2通过滚动面板回归,获得回归系数(5)在式(2)中,Cosi,t-12→t-1表示第(t-12)月～第(t-1)月的Cos值;其它变量以此类推..

Cosi,t-12→t-1=μ+ρCosi,t-13→t-2+

θYi,t-13→t-2+φXi,t-13+

εi,t-12→t-1

(2)

步骤3预测第t月的Cos,并将其作为前瞻系统性偏度(PSS).

(3)

步骤4在计算出个股的前瞻系统性偏度(PSS)后,结合市值和前瞻系统性偏度(PSS)对个股进行2×3的分组,并在每个月末对分组进行重新调整,然后将前瞻系统性偏度(PSS)最低的30%股票与前瞻系统性偏度(PSS)最高的30%股票的加权收益率之差作为前瞻系统性偏度(PSS)因子.

1.1.2 异质性偏度及PIS因子的构建

Ghysels等[16]提出了一种基于分位数度量偏度的方法,如下式

QSK(xt)=

(4)

其中q0.95(·)、q0.50(·)和q0.05(·)分别代表95%、50%和5%分位数.再考虑三阶矩CAPM模型

ri,t-rf,t=βM,i,tμM,t+βM2,i,tμM2,t+εi,t

(5)

1.1.3 总体偏度及PTS因子的构建

将个股收益率ri,t代入式(4),QSK(ri,t)即为总体偏度.与前瞻系统性偏度(PSS)因子类似,重复PSS因子构建的四个步骤,在QSK(ri,t)的基础上构建前瞻总体偏度(PTS)因子.

1.2 数据来源和描述性统计

1.2.1 数据来源

由于我国股票市场上存在一些财务质量过低、股价波动非理性程度明显过高的股票,在实证研究中会对定价因子的收益率造成严重影响,因此本研究在样本中将这些股票剔除,包括ST股、待退市股、B股、次新股(上市未满一年)和净资产为负的股票.此外,Liu等[33]认为我国股票市场存在壳价值污染,因此在实证研究中剔除了市值最小的30%股票.考虑到在不同市值组中,BM和ROE等变量对投资组合收益率的影响可能存在差异,为了不影响其它定价因子的构建,本研究同时剔除了市值最大和市值最小的5%股票.最终的股票样本为3 176支,样本区间为1999年1月—2021年7月.原始数据的名称、频率和来源如下表所示.

1.2.2 定价因子的描述性统计

在后文的实证研究中,主要借助CAPM、三因子模型、四因子模型和五因子模型,这里将三个前瞻偏度因子和上述模型中的经典定价因子总结如表3所示.需要说明的是,所有定价因子在计算中都采用分组变量最低的 30% 股票与分组变量最显著.均值和标准差都进行了年化处理.此外,由于沪深300等指数的推出时间较晚,因此本研究以上证指数作为市场指数.

从表3中可以看出:PSS因子、PIS因子和PTS因子显著为正.与PSS、PIS和PTS较高的股票相比,PSS、PIS和PTS较低的股票分别获得年均3.50%、5.06%和5.46%的超额收益.此外,PSS因子、PIS因子和PTS因子的夏普比率也远远大于市场因子(MKT).

在经典定价因子中,市值因子(SMB)显著为正说明小市值股票的收益高于大市值股票,且平均每年高出9.08%;价值因子(HML)显著为负则说明低BM组股票的收益低于高BM组,且平均每年低出7.54%.此外,动量因子(MOM)、投资因子(CMA)和盈利因子(RMW)均不显著.

图1是PSS因子、PIS因子、PTS因子和市场因子的累计收益率对比.可以看出:2000年1月—2021年7月,PSS因子、PIS因子和PTS因子的累计收益率显著跑赢市场.这说明从长期来看,与PSS、PIS和PTS较高的股票相比,PSS、PIS和PTS较低的股票可以获得更高的收益.

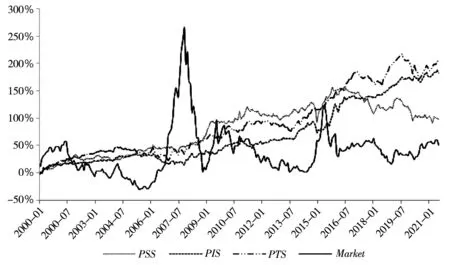
图1 PSS因子、PIS因子、PTS因子和市场因子的累计收益率

本研究认为风险厌恶型投资者在市场中占据主体.就系统性偏度而言,若个股在过去12个月中呈现出正的系统性偏度,那么在一致性预期下,投资者外推本月的系统性偏度仍然为正.在构建投资组合时,风险厌恶型投资者通常会买入这类股票来抵御市场波动,进而导致这类股票的价格被高估.因此在当月乃至后续几个月中,系统性偏度较高的股票会获得相对较差的收益,这也是PSS因子显著为正的原因.从长期来看,与PSS较高的股票相比,PSS较低的股票可以获得更高的收益.

对于异质性偏度和总体偏度,根据本研究定义,二者反映的都是股票收益分布的非对称性.事实上,异质性偏度和总体偏度为正的股票在未来有极低的概率可以获得高额正收益,故这类股票本质上是一种“彩票型股票”.以往的研究发现[34-36]:投资者通常会高估“彩票型股票”获得高额正收益的概率,从而表现出对它们的偏好,最终推高其当期价格并降低未来收益.因此与“非彩票型股票”相比,“彩票型股票”的未来平均收益显著偏低,这也是PIS因子和PTS因子显著为正的原因.从长期来看,与PIS和PTS较高的股票相比,PIS和PTS较低的股票可以获得更高的收益.

1.2.3 特征信息对偏度预测的影响

在1.1.1节～1.1.3节,本研究将上市公司的特征信息引入偏度的预测过程,分别构建了前瞻系统性偏度(PSS)、前瞻异质性偏度(PIS)和前瞻总体偏度(PTS).接下来,本节将比较引入和不引入上市公司特征信息对偏度预测的影响.

首先,重复1.1.1节的四个步骤,但在式(2)中不引入表1的一系列控制变量,重新构建不引入上市公司特征信息的前瞻系统性偏度(PSSN)、前瞻异质性偏度(PISN)和前瞻总体偏度(PTSN);其次,计算引入和不引入上市公司特征信息的两组前瞻偏度与真实偏度之间的差异(6)如1.1.1节～1.1.3节所示,本研究构建的引入和不引入上市公司特征信息的前瞻偏度,都是基于第(t-12)月～第(t-1)月的信息所得到的预测值,是事前的;真实偏度值需要在市场完成第t月的交易后才能得到,是事后的.因此,比较二者的差异可以反映对未来偏度的预测精度.,并采用均方误差(MSE)和平均绝对误差(MAE)对这种差异进行度量.结果如下表所示.

表1 变量名称及定义

表2 原始数据名称、频率和来源

表3 定价因子的描述性统计

从表4中可以看出:无论系统性偏度、异质性偏度还是总体偏度,引入上市公司特征信息都能降低均方误差(MSE)和平均绝对误差(MAE),这表明引入上市公司特征信息可以提升对未来偏度的预测精度.

表4 特征信息对偏度预测的影响

2 前瞻偏度因子的有效性检验

从描述性统计来看,通过做多PSS、PIS和PTS较低的股票并同时做空PSS、PIS和PTS较高的股票,投资者可以获得比市场更高且更稳定的收益.接下来,本节将采用Fama-Macbeth回归、双变量检验和组间差异分析等方法,系统地检验三个前瞻偏度因子在我国股票市场的定价效应.

2.1 PSS因子的有效性检验

国内现有研究所提及的偏度,几乎全部是指异质性偏度或总体偏度.对于系统性偏度,只有部分学者检验了三阶矩CAPM模型在我国股票市场的适用性,且没有学者对高次项系数的经济学含义进行明确定义,也没有学者将系统性偏度因子视作独立的定价因子进行实证研究,因此本研究将系统性偏度作为重点研究对象.

2.1.1 Fama-Macbeth回归

根据三个双变量组——PSS/SIZE、PSS/BM以及PSS/ROE,分别构建25(5×5)个投资组合,并将PSS因子分别引入CAPM、三因子模型、四因子模型和五因子模型,借助Fama-Macbeth回归,检验PSS因子对上述75个投资组合的收益是否有显著影响.结果如表5所示.

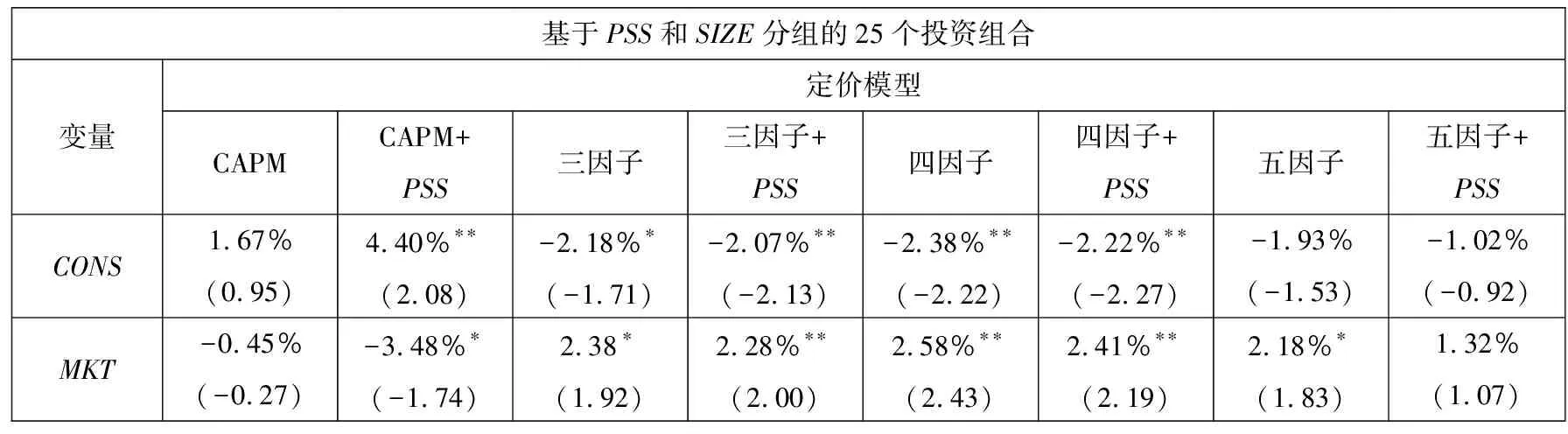
表5 Fama-Macbeth回归结果

从表5中可以看出:PSS因子对上述75个投资组合的收益有显著影响,且PSS因子的符号为正.这说明:1)考虑上市公司特征信息的前瞻系统性偏度(PSS)因子,是我国股票市场的有效定价因子.2)与PSS较高的投资组合相比,PSS较低的投资组合可以获得更高的收益.对于以PSS和SIZE分组的25个投资组合,PSS较低的投资组合平均每月可以获得0.21%～0.41%的超额收益;对于以PSS和BM分组的25个投资组合,PSS较低的投资组合平均每月可以获得0.28%～0.44%的超额收益;对于以PSS和ROE分组的25个投资组合,PSS较低的投资组合平均每月可以获得0.42%～0.47%的超额收益.

2.1.2 双变量组间差异检验

在上述实证结果的基础上,本节继续对前瞻系统性偏度(PSS)进行双变量检验.依次选取PSS/BM、PSS/MOM和PSS/SIZE三个双变量组,分别构建25(5×5)个投资组合并计算每个组合的月度加权收益率,并比较不同PSS分组(低、中低、中、中高、高)的收益率组间差异,如下表所示.

从表6中可以看出:除PSS/SIZE分组中的高市值组外,随着PSS从低到高,三个双变量组其它投资组合的加权收益率呈现出逐渐变小的趋势.从显著性来看:1)对于以PSS和BM分组的25个投资组合,与高PSS组的股票相比,低PSS组的股票在中低BM、中BM、中高BM和高BM组中分别可以获得月均0.62%、0.40%、0.43%和0.65%的超额收益,在低BM组中没有显著差异;2)对于以PSS和MOM分组的25个投资组合,与高PSS组的股票相比,低PSS组的股票在低MOM、中低MOM、中MOM和中高MOM组中分别可以获得月均0.70%、0.56%、0.48%和0.42%的超额收益,在高MOM组中没有显著差异;3)对于以PSS和SIZE分组的25个投资组合,与高PSS组的股票相比,低PSS组的股票在低市值和中低市值组中分别可以获得月均0.44%和0.65%的超额收益,在中市值、中高市值和高市值组中没有显著差异.更进一步,将低PSS组和高PSS组的收益率之差作为一个新的投资组合,该组合意味着做多PSS较低的股票,同时做空PSS较高的股票.考察新投资组合CAPM α值的显著性,结果与上述结论类似.

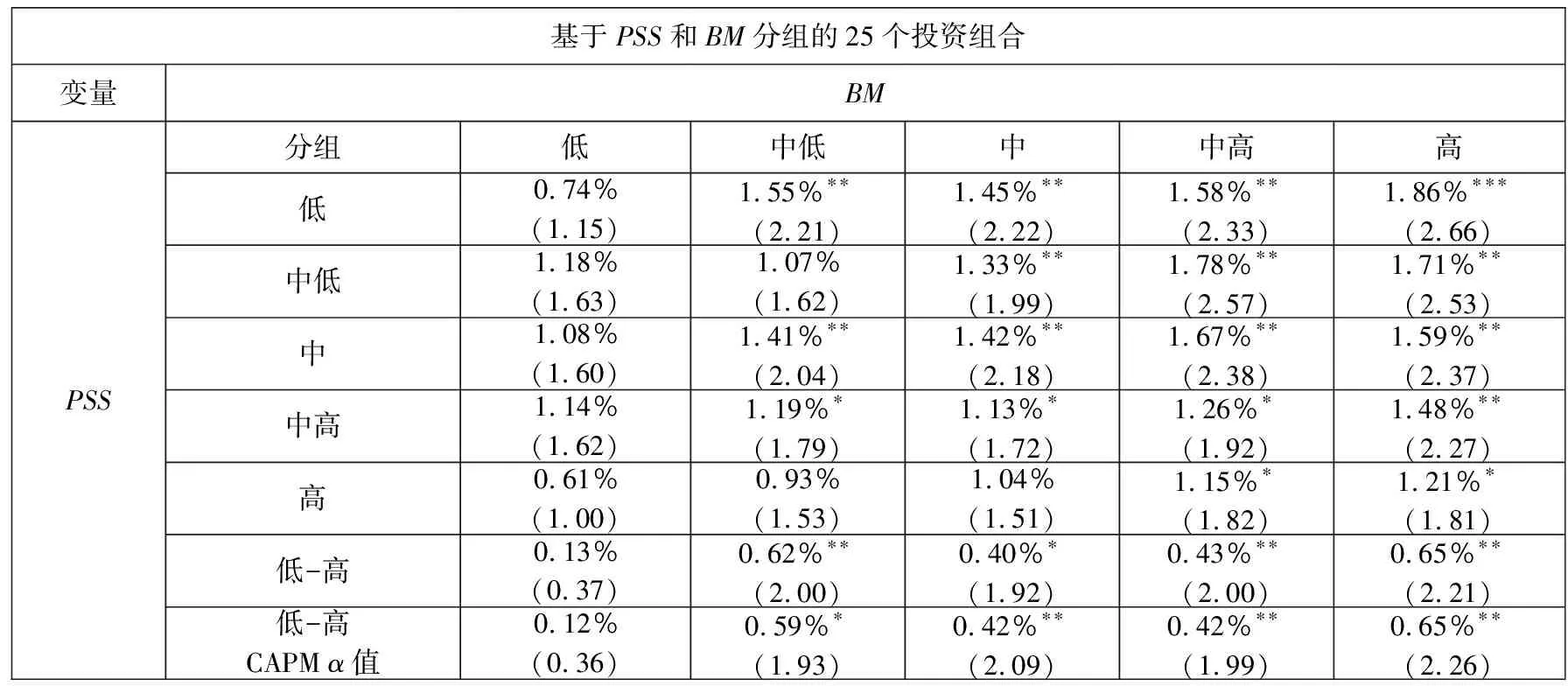
表6 双变量组间差异检验

2.2 PIS因子的有效性检验

本节根据PIS的数值将股票样本分成三组(7)基于PIS的三个分组为:低(PIS最低的30%股票)、中(PIS居中的40%股票)和高(PIS最高的30%股票).,然后基于因子模型,通过分析组间差异检验PIS因子的有效性,如下表所示.

从表7中可以看出:无论CAPM、三因子模型、四因子模型还是五因子模型,α值在PIS较低的投资组合与PIS较高的投资组合之间存在显著差异.与PIS较高的投资组合相比,PIS较低的投资组合每月可以获得0.7%～1.2%的超额收益.此外,SMB因子始终对解释投资组合的组间差异有显著贡献,且SMB因子的数值与投资组合的组间差异同方向变动;MKT因子在CAPM、三因子模型和四因子模型中对解释投资组合的组间差异有显著贡献,且MKT因子的数值与投资组合的组间差异反方向变动;HML因子在三因子模型和四因子模型中对解释投资组合的组间差异有显著贡献,且HML因子的数值与投资组合的组间差异同方向变动;在四因子模型中,MOM因子对解释投资组合的组间差异有显著贡献,且与投资组合的组间差异同方向变动.

2.3 PTS因子的有效性检验

与PIS因子的有效性检验相同,本节根据PTS的数值将股票样本分成三组(8)基于PTS的三个分组为:低(PTS最低的30%股票)、中(PTS居中的40%股票)和高(PTS最高的30%股票).,然后基于因子模型,通过分析组间差异检验PTS因子的有效性,如表8所示.

表8 基于PTS分组的组间差异检验

从表8中可以看出:无论CAPM、三因子模型、四因子模型还是五因子模型,α值在PTS较低的投资组合与PTS较高的投资组合之间存在显著差异.与PTS较高的投资组合相比,PTS较低的投资组合每月可以获得0.4%～0.9%的超额收益.此外,SMB因子和PSS因子始终对解释投资组合的组间差异有显著贡献,且SMB因子和PSS因子的数值与投资组合的组间差异同方向变动;在四因子模型中,MOM因子对解释投资组合的组间差异有显著贡献,且与投资组合的组间差异同方向变动;在五因子模型中,CMA因子和RMW因子对解释投资组合的组间差异有显著贡献,其中CMA因子的数值与投资组合的组间差异同方向变动,RMW因子的数值与投资组合的组间差异反方向变动.

3 前瞻偏度因子的稳健性检验

在前文中,通过实证研究发现前瞻系统性偏度(PSS)因子、前瞻异质性偏度(PIS)因子和前瞻总体偏度(PTS)因子在我国股票市场上有显著的定价效应.接下来,本节将借助因子间的相关性检验和回归分析以及GRS检验,判断三个前瞻偏度因子是否为冗余因子.

3.1 因子间的相关性检验

首先检验因子间的相关性,并将其分为两部分,即因子收益率的时间序列相关性和变量间的横截面相关性.

3.1.1 时间序列相关性检验

基于前瞻偏度因子和经典定价因子的收益率时间序列,计算了定价因子两两之间的皮尔逊相关系数,如表9所示.

表9 因子间的时间序列相关性

从表9中可以看出:在三个前瞻偏度因子内部,PSS因子和PIS因子之间的相关性较低,皮尔逊相关系数为0.09;PTS因子与PSS因子、PIS因子之间的相关性稍强,皮尔逊相关系数分别为0.21、0.26.

从三个前瞻偏度因子和经典定价因子之间来看:1)PSS因子与SMB因子之间的相关性稍强,皮尔逊相关系数为0.25,与其它定价因子之间的皮尔逊相关系数绝对值均不超过0.14; 2)PIS因子与MOM因子之间的相关性最弱,皮尔逊相关系数为0.07,与其它定价因子之间的皮尔逊相关系数绝对值介于0.19和0.39之间; 3)PTS因子与MKT因子之间的相关性最弱,皮尔逊相关系数为-0.03,与其它定价因子之间的皮尔逊相关系数绝对值介于0.32和0.56之间.因此从整体来看,三个前瞻偏度因子与经典定价因子之间的时间序列相关性较弱.

3.1.2 横截面相关性检验

在构建PSS因子、PIS因子、PTS因子、SMB因子、HML因子、MOM因子、CMA因子和RMW因子时,分别基于市值和前瞻系统性偏度(PSS)、前瞻异质性偏度(PIS)、前瞻总体偏度(PTS)、BM、MOM、INV和ROE等变量构建了2×3的分组.接下来,将检验这些变量的横截面相关性,共分为两步:第一,在每个时间截面(第t月)计算上述变量两两之间的皮尔逊相关系数;第二,将全部T个月皮尔逊相关系数的平均值作为该组变量间的横截面相关系数,结果如下表所示.

表10的结论与表9类似:在三个前瞻偏度内部,前瞻系统性偏度(PSS)和前瞻异质性偏度(PIS)之间的相关性最低,平均横截面相关系数为-0.01;前瞻总体偏度(PTS)与前瞻系统性偏度(PSS)、前瞻异质性偏度(PIS)之间的相关性稍强,平均横截面相关系数分别为0.24、0.48.

表10 变量间的横截面相关性

在三个前瞻偏度和其它变量之间:1)前瞻系统性偏度(PSS)与其它五个变量之间的平均横截面相关系数绝对值均不超过0.17;2)前瞻异质性偏度(PIS)与MOM之间的相关性稍强,平均横截面相关系数为0.28,与其它四个变量之间的平均横截面相关系数绝对值均不超过0.15;3)前瞻总体偏度(PTS)与INV之间的相关性最弱,平均横截面相关系数为0.08,与其它四个变量之间的平均横截面相关系数绝对值介于0.20和0.42之间.因此从整体来看,三个前瞻偏度与其它五个变量之间的横截面相关性也较弱.

3.2 因子间的回归分析

本节通过三个前瞻偏度因子对其它定价因子做线性回归,基于截距项的显著性来评估是否存在遗漏变量,进而判断三个前瞻偏度因子是否为冗余因子.

3.2.1PSS因子的回归分析

PSS因子和其它因子间的回归分析如表11所示.

表11 PSS因子和其它因子间的回归分析

从表11中可以看出:PSS因子对其它因子进行线性回归时,截距项始终对PSS因子有显著影响,这意味着PSS因子包含了其它因子所不具备的信息.其中,SMB因子和HML因子对PSS因子有显著的正向影响.

就三个前瞻偏度因子而言:1)由于截距项始终显著,因此PSS因子包含了PIS因子和PTS因子所不具备的信息;2)向回归模型中加入PTS因子,可以提高Adj.R2且βPTS显著为正,因此PTS因子对PSS因子有较好的解释作用;3)向模型中加入PIS因子,Adj.R2没有得到明显提高且βPIS不显著,因此PSS因子和PIS因子之间不存在显著的相关关系.

3.2.2PIS因子的回归分析

PIS因子和其它因子间的回归分析如表12所示.

表12 PIS因子和其它因子间的回归分析

从表12中可以看出:PIS因子对其它因子进行线性回归时,截距项始终对PIS因子有显著影响,这意味着PIS因子包含了其它因子所不具备的信息.其中,MKT因子对PIS因子有显著的负向影响,SMB因子、HML因子和MOM因子对PIS因子有显著的正向影响.

就三个前瞻偏度因子而言:1)由于截距项始终显著,因此PIS因子包含了PSS因子和PTS因子所不具备的信息;2)向回归模型中加入PTS因子,可以提高Adj.R2且βPTS显著为正,因此PTS因子对PIS因子有较好的解释作用;3)向模型中加入PSS因子,Adj.R2没有得到明显提高且βPSS不显著,因此PSS因子和PIS因子之间不存在显著的相关关系,这与3.2.1节的结论一致.

3.2.3PTS因子的回归分析

PTS因子和其它因子间的回归分析如表13所示.

表13 PTS因子和其它因子间的回归分析

从表13中可以看出:PTS因子对其它因子进行线性回归时,截距项始终对PTS因子有显著影响,这意味着PTS因子包含了其它因子所不具备的信息.其中,SMB因子、MOM因子和CMA因子对PTS因子有显著的正向影响,HML因子和RMW因子对PTS因子有显著的负向影响.

就三个前瞻偏度因子而言:1)由于截距项始终显著,因此PTS因子包含了PSS因子和PIS因子所不具备的信息;2)向回归模型中加入PSS因子和PTS因子,都可以提高Adj.R2且βPSS和βPTS均显著为正,因此PSS因子和PIS因子都对PTS因子有显著的解释作用,这与3.2.1节和3.2.2节的结论一致.

根据本研究的定义,系统性偏度和异质性偏度度量的是总体偏度的不同成分,这也是PSS因子和PIS因子对PTS因子有显著的解释作用,而PSS因子和PIS因子之间不存在显著相关关系的原因.

3.2.4 截距项的进一步检验

从表14中可以看出:无论以何种方式分组,五因子模型中四个指标的数值均明显低于三因子模型和四因子模型,因此五因子模型在我国股票市场的解释力整体优于三因子模型和四因子模型.三个前瞻偏度因子比较来看:向定价模型中引入PIS因子,对于模型解释力的提升效果最为明显;向定价模型中引入PTS因子,对于模型解释力的提升效果最弱;PSS因子对于模型解释力的提升效果在大部分模型中介于PIS因子和PTS因子之间.此外,同时向定价模型中引入PSS因子和PTS因子,对于模型解释力的提升效果最弱;同时向定价模型中引入PSS因子和PIS因子,与同时向定价模型中引入PIS因子和PTS因子,在不同模型中互有优劣.如果同时引入三个前瞻偏度因子,三因子模型、四因子模型和五因子模型的解释力会得到明显提升.

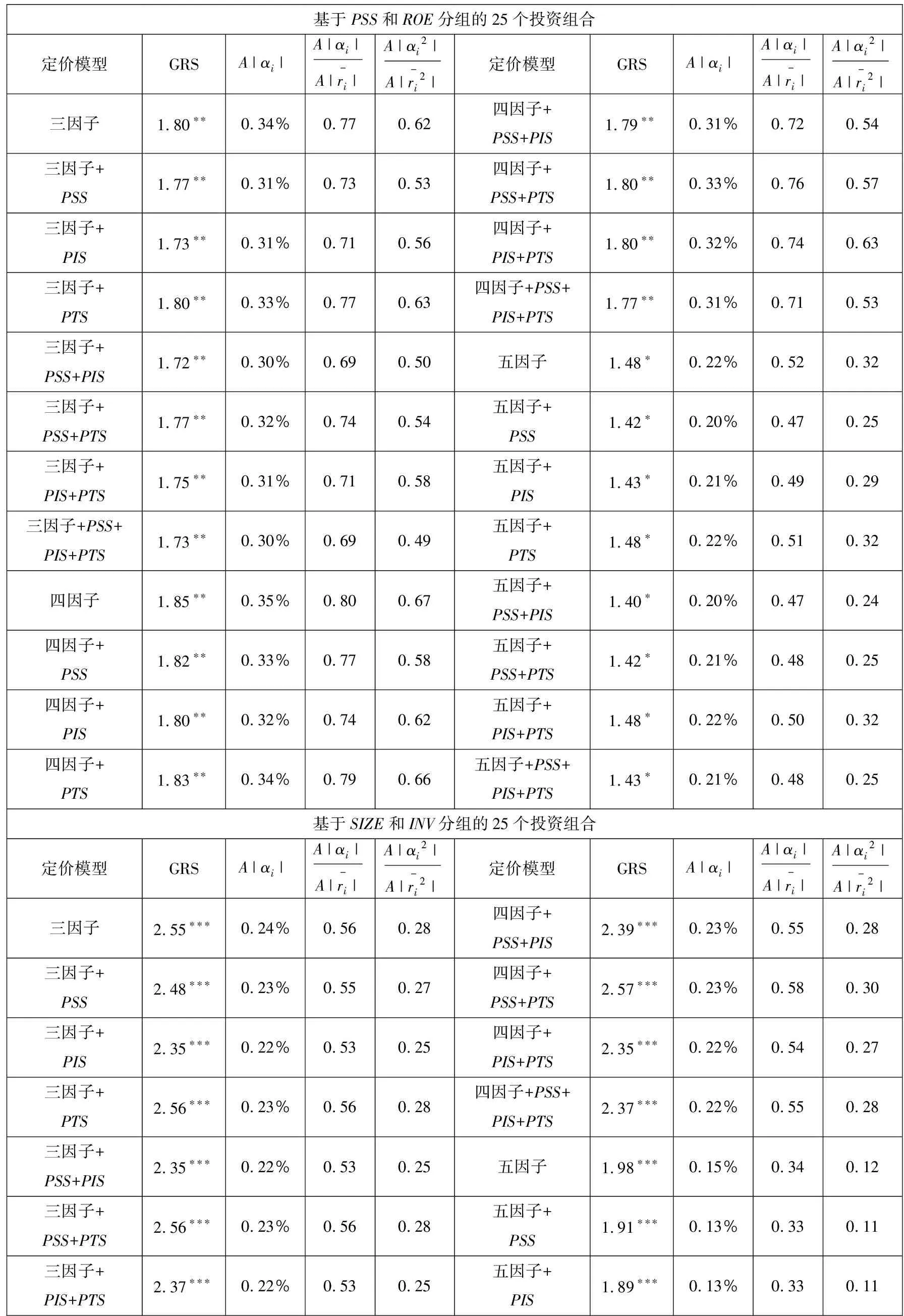
表14 截距项的进一步检验

3.3 前瞻偏度因子的分时期检验

表15 股权分置改革前后的截距项检验

4 结束语

自股票市场诞生以来,如何在不确定的环境中解释股价的未来变化,一直是金融学研究的重要主题.就我国而言,一方面,金融资产的价格引导着经济资源的配置方向,也影响着产业结构和实体经济的发展方向;另一方面,随着我国股票市场逐渐走向成熟,越来越多的投资者不再仅仅关注股票价格的盘面变动,而是更加关注股价变动背后的深层次原因.因此,在当前的市场背景和经济环境下,资产定价理论的发展有着非常重要的现实意义,也被研究者和投资者所广泛关注.

本研究方法主要克服了以往研究中存在的三大问题:1)忽视上市公司的特征信息,对未来偏度的预测能力存在不足;2)没有将偏度分为系统性偏度、异质性偏度和总体偏度进行讨论,研究框架的完整性存在不足;3)没有把偏度因子作为独立的定价因子引入三因子模型、四因子模型和五因子模型,实证结果的稳健性存在不足.综上所述,本研究为检验偏度因子在我国股票市场的定价效应提供了更为完整的研究框架和更为稳健的实证结果.同时,本研究结果也为投资者提供了三个极具操作性的定价因子:通过做多PSS、PIS和PTS较低的股票,并同时做空PSS、PIS和PTS较高的股票,投资者可以获得显著的超额收益.从长期来看,这些投资组合的累计收益显著高于市场,且组合收益的波动性远远低于市场.