AlNi3单轴拉伸的分子动力学模拟
2023-11-20戴长军刘晓波
戴长军, 刘晓波
(南昌航空大学 航空制造工程学院,南昌 330063)
0 引言
近年来,随着国内航空、航天等行业的快速发展,对镍基合金材料的需求也越来越大[1],要求也更高。在现代航空发动机中,镍基合金材料的用量占发动机总重量的40%~60%[2],如航空涡轮叶片、涡轮盘等均使用该合金材料。镍基合金具有很好的稳定性[3]、极高的强度、优良的耐腐蚀性和抗氧化性、良好的塑性和焊接性,以及较高的综合力学性能,是一种使用范围广泛、应用前景良好的合金材料。
分子动力学模拟在材料科学中的应用十分广泛,也取得了许多成果。Gowthaman等[4]通过分子动力学模拟研究了温度对Ni2Al3析出相拉伸特性的影响,发现Ni2Al3析出相材料对温度的变化非常敏感。刘晓波等[5]研究了温度和应变率对Al2Cu拉伸性能的影响,结果表明,升高温度会使Al2Cu的塑性变强,拉伸强度明显降低;还发现在应变率0.005~0.006 ps-1之间存在某个值,当应变率超过该值时,拉伸产生的空位会聚集在发射处使体系内出现大量孔洞。Krasnikov等[6]研究了纳米孔洞的生长对单晶铝拉伸性能的影响,结果表明升高温度会使其抗拉强度降低,减小孔洞半径与体系尺寸之比会使其抗拉强度变大。Mayer等[7]建立了金属Al纳米粉末压缩的力学模型,研究了Al纳米粉末在压缩变形条件下的力学性能,结果表明,建立的模型能较好地描述粉末压缩阶段温度是影响其弹性模量变化的主要因素。Afkham等[8]模拟研究了AlCrCoFeCuNi合金在高温条件下的拉伸性能,结果表明,随着温度升高,其屈服应力明显降低,合金在所有模拟条件下表现出很好的塑性。Gowthaman等[9]模拟研究了应变速率和温度对FeNi析出相极限应力和应变的影响,结果表明温度的变化对FeNi析出相的影响比应变速率的变化更加明显。Li等[10]研究了Al/Ni单晶的拉伸力学性能,对Al-Ni纳米多层膜、单晶铝和单晶镍的力学性能进行了比较。研究结果发现,Al-Ni的弹性模量比单晶铝高,但比单晶镍低。Han等[11]研究了单轴拉伸和压缩镀镍石墨烯铝基复合材料的力学性能,发现在拉伸条件下可以通过镀镍的方法来改善材料的性能,在压缩条件下,镍涂层石墨烯可以加强材料的塑性变形效果。Tang等[12]研究了含孔洞单晶γ-TiAl的力学性能,发现孔洞会因为位错不断产生和剪切环的扩展不断生长,随着孔洞体积分数的增加,其拉伸强度和弹性模量会减小,而应变速率的增加会使拉伸强度变大。朱旭等[13]采用分子动力学方法研究Ni/Ni3Al的拉伸力学性能,发现γ′强化相可以提高Ni/Ni3Al的抗拉强度,还发现抗拉强度对高应变速率敏感。李源才等[14]对单晶/多晶镍(SPSNi)的拉伸力学性能进行模拟,发现单晶/多晶界面会使拉伸后界面处非晶化程度加剧,易于萌生孔洞。
在镍基合金的变形过程中,通常认为对位错起阻碍作用的是AlNi3强化相,这是镍基合金具有优异高强度的根本原因。温度和应变速率的变化会对强化相AlNi3的力学性能产生显著的影响,而强化相AlNi3会决定镍基合金材料的力学特性。因此,有必要对镍基合金强化相AlNi3进行分析。但材料在实际生产过程中会产生孔洞、形成微裂纹等缺陷,导致材料的断裂失效[15]。因此,也有必要对含孔洞的AlNi3进行研究。本研究通过分子动力学方法模拟AlNi3的单轴拉伸变形,利用LAMMPS软件建立了AlNi3模型,研究不同温度、不同应变速率对AlNi3力学性能的影响;建立含预制孔洞的AlNi3模型,通过设置不同大小的孔洞以及孔洞数量对其力学性能进行研究。对AlNi3进行拉伸模拟,探究原子在微观层次下的运动与力学性能的联系,对AlNi3理论研究和实际应用具有重要意义。
1 建立AlNi3模型与模拟方法
利用LAMMPS软件建立模型盒子,在X、Y、Z3个方向上均设置周期性边界。模拟盒子的长度应当设置成晶格常数的整数倍,可防止原子在盒子边界处产生重叠。在X和Y方向都重复20次,Z方向重复40次,建立20a0×20b0×40c0的AlNi3初始模型,实际大小为7.136 nm×7.136 nm×14.272 nm,总计64000个原子。其中,[100]晶向对应图1中空间坐标系的X轴,[010]对应Y轴,[001]对应Z轴,AlNi3晶格常数a0=b0=c0=0.3568 nm。该模型按照理想晶格排列建立,AlNi3模型所有原子的总能量处于非平衡状态,原子模型存在较大预应力和势能。因此,在对AlNi3模型进行模拟拉伸之前,要对该模型进行弛豫,将AlNi3模型在300 K、NPT系综条件下运行20000步,时间步设置为0.01 ps。经充分弛豫后的模型如图1所示。
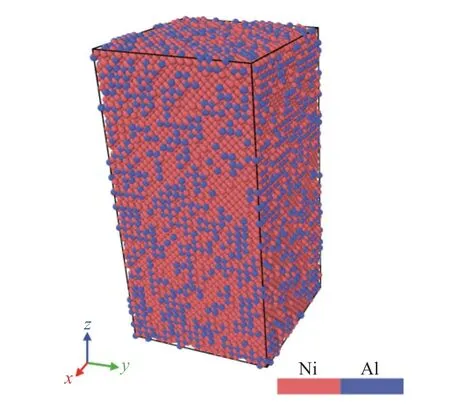
图1 AlNi3模型Fig.1 AlNi3 model
模拟拉伸中的嵌入原子法即为EAM势,是通过将晶体总的势能分为在晶格点阵上的原子之间的相互作用势能及在电子云背景下的原子嵌入能2个部分的方法。EAM势函数表达式为:
式中:rij表示原子i和原子j之间的距离;ρi表示第i原子以外的其他原子在第i原子处产生的电子密度总和;分布函数f(r)表示原子的电子密度。在模拟计算金属体系时,EAM势的应用十分广泛,其计算量不会增加,且计算效率高。因此,本研究选用EAM势对单晶AlNi3模型进行模拟计算。
2 结果与分析
2.1 AlNi3单轴拉伸变形模拟
2.1.1 300 K下AlNi3拉伸变形结果分析
将弛豫后的模型在300 K温度下沿Z轴匀速拉伸。通过Nose-Hoover热浴法使温度保持稳定,选用NVT系综和Deform拉伸方式,3个方向选用周期性边界,时间步设置为0.01 ps,工程应变速率设置为0.0002 ps-1。对模型进行拉伸,持续105步,期间每100步输出原子坐标、温度、原子势能、动能、总能量、应力和应变等信息。通过Ovito软件对模拟体系进行处理,将模拟计算得到的数据绘制应力-应变曲线图,如图2所示。图3为不同应变对应的原子轨迹图。
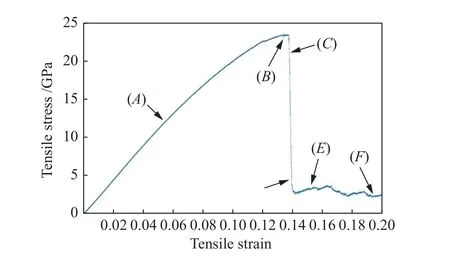
图2 AlNi3拉伸应力-应变曲线图Fig.2 Tensile stress-strain curve of AlNi3

图3 原子轨迹图(a~f分别对应A~F的内部切片局部图)Fig.3 Atomic trajectory diagram (a~f correspond to the local diagrams of the internal sections of A~F)
由图2可知,AlNi3模型经过2×104步弛豫后,其初始应力为0;在应变ε小于0.0600时(图2中的A点处),AlNi3模型发生弹性变形(图3A),应力-应变曲线可近似看作直线,满足胡克定律,根据应力应变计算出拉伸弹性模量E=220.749 GPa;当ε=0.1320时,原子模型如图3B所示;当ε增加到0.1342时,σ达到峰值23.397 GPa(图2中B点处)。当ε=0.1380时,可以观察到原子体系表面位错的产生(图3C);当ε=0.1384时开始萌生孔洞(图3D);随着应变不断增加,原子内部的孔洞也会不断快速长大(图3E);当ε=0.1940时,模型内部的微小孔洞发展成如图3F所示的巨大贯穿孔洞。模拟体系并没有发生宏观上拉断的现象,这是因为模型在3个方向上均设置为周期性边界,相当于模拟体系的盒子是无限大,不会存在宏观拉断的现象。
在300 K下,AlNi3表现出较强的脆性,通过观察图2的E、F阶段可以得到,应变在0.1500之后基本趋于稳定。
2.1.2 不同温度下AlNi3拉伸结果分析
为了研究AlNi3的拉伸力学性能是否与温度有关,在300、400、500、600、700、800、900 K温度下分别对AlNi3模型进行拉伸。不同温度下的应力-应变曲线如图4所示。
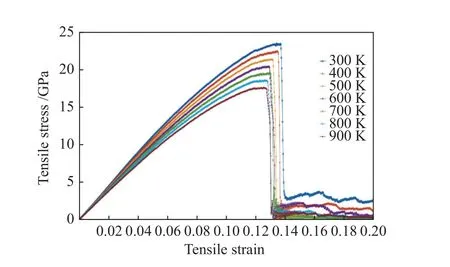
图4 不同温度下AlNi3拉伸应力-应变曲线图Fig.4 Tensile stress-strain curves of AlNi3 at different temperatures
从图4可以看出,当应变小于0.06时,各温度下的应力-应变曲线近似为直线,可认为AlNi3均存在弹性变形阶段。当温度分别为300、400、500、600、700、800、900 K时,计算得到对应的弹性模量分别为220.749、214.301、207.500、200.838、194.592、187.856、181.752 GPa,抗拉强度分别为23.397、22.380、21.313、20.337、19.452、18.511、17.573 GPa,不同温度与弹性模量、抗拉强度的关系如图5所示。由图5可以看出,AlNi3模型对不同温度变化十分敏感,当温度由300 K升高至900 K,弹性模量和抗拉强度均随温度的升高呈下降趋势。
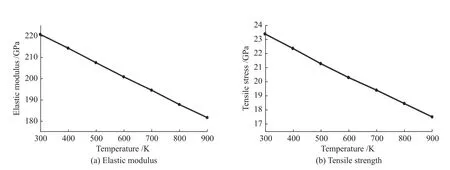
图5 不同温度下的弹性模量和抗拉强度Fig.5 Elastic modulus and tensile strength at different temperatures
2.1.3 不同应变速率下AlNi3拉伸结果分析
为了研究AlNi3拉伸力学性能与应变速率的关系,设置温度为300 K,选取0.0002、0.0005、0.0010、0.0040、0.0100 ps-15组应变速率。不同应变速率下AlNi3模型拉伸的应力-应变曲线如图6所示。
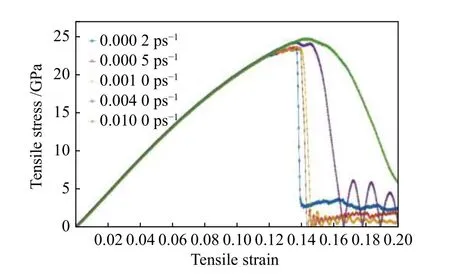
图6 不同应变速率的应力-应变曲线图Fig.6 Stress-strain curves at different strain rates
从图6可以看到,在AlNi3拉伸的弹性变形阶段,5条曲线几乎完全重合,表明不同的应变速率对弹性模量的影响不大。当应变速率分别为0.0002、0.0005、0.0010、0.0040、0.0100 ps-1时,弹性模量分别为220.749、219.517、217.296、221.361、218.563 GPa,抗拉强度分别为23.397、23.500、23.558、24.151、24.669 GPa。图7为应变速率与弹性模量、抗拉强度的关系曲线,可以看出,应变速率对AlNi3模型弹性模量影响较小,而增加应变速率会在一定程度上造成AlNi3抗拉强度和断裂应变的升高。
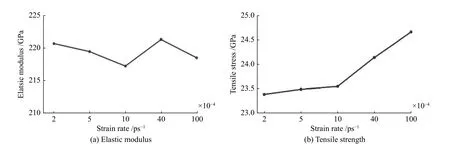
图7 不同应变速率下的弹性模量和抗拉强度Fig.7 Elastic modulus and tensile strength at different strain rates
2.2 预制孔洞AlNi3单轴拉伸变形模拟
2.2.1 300 K含预制孔洞AlNi3拉伸结果分析
在该模型中心的位置(10a0,10b0,20c0)建立一个半径R为2a0=0.7136 nm的球形区域,删除了139个原子,最后模型共有63861个原子,如图8所示。
将含预制孔洞的AlNi3模型在300 K、NVT条件下沿Z轴匀速进行拉伸模拟,3个方向上边界条件选用周期性边界,时间步设置为0.01 ps,应变速率为0.0002 ps-1,拉伸步长持续105步,每隔100步输出原子坐标信息、应力和应变等数据,将计算得到数据绘制成应力-应变曲线,如图9所示。
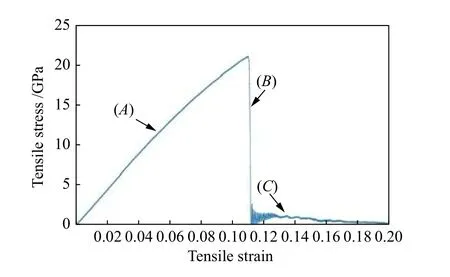
图9 含预制孔洞AlNi3拉伸应力-应变曲线图Fig.9 Tensile stress-strain curve of AlNi3 with prefabricated voids
含预制孔洞AlNi3模型在拉伸初期阶段发生了弹性变形,应力-应变关系可近似看作直线(图9中A段),计算得到其弹性模量为219.611 GPa;在应变为0.1096时达到应力峰值,抗拉强度为21.047 GPa;随着应变继续增加,应力骤然下降(图9中B段);在应变达到0.1200后,应力趋于稳定(图9中C段)。利用Ovito软件对含预制孔洞AlNi3模型进行分析,可以得到不同应变对应的原子轨迹图,如图10所示。

图10 不同应变下的原子轨迹图(a~d分别对应A~D的内部切片局部图)Fig.10 Diagram of atomic trajectories under different strains(Figures a~d correspond to the sections of A~D)
由图10可以得到:当ε=0.0526时,含预制孔洞AlNi3模型仍然处于弹性变形阶段,没有明显空位产生(图10a);当ε=0.1106时,孔洞周围开始出现空位,孔洞变大,并开始有向Y、Z轴方向发展长大的迹象,且沿Z轴方向长大的速度小于沿Y轴方向的速度(图10b);继续运算且ε增大时,孔洞吸收周围空位不断长大(图10c、图10d)。当ε=0.1096时,应力达到最大值21.047 GPa,而ε=0.1114时其应力为2.024 GPa。
将不含预制孔洞和含预制孔洞的AlNi3模型拉伸应力-应变曲线进行对比分析,如图11所示。由结果可知:不含预制孔洞和含预制孔洞的AlNi3模型在弹性变形阶段的曲线基本重合,不含预制孔洞模型的弹性模量为220.749 GPa,含预制孔洞模型的弹性模量为219.611 GPa;不含预制孔洞模型抗拉强度为23.397 GPa,而预制半径为2a0的孔洞会使AlNi3的抗拉强度减小,为21.047 GPa,下降了10.04%,对应的极限应变也从0.1342变为0.1096。这说明预制孔洞会降低抗拉强度,但对弹性模量的影响较小。

图11 不含孔洞和含孔洞AlNi3模型应力-应变曲线图Fig.11 Stress-strain curves of AlNi3 models without/with voids
2.2.2 不同预制孔洞尺寸的AlNi3拉伸结果分析
建立5组不同预制孔洞尺寸的初始模型,大小为20a0×20b0×40c0,均在模型的中心位置(10a0,10b0, 20c0)。5组模型预制孔洞的具体参数见表1,分别标注为1#~5#,模型切面如图12所示。

表1 不同预制孔洞尺寸参数Table 1 Size parameters of different prefabricated voids
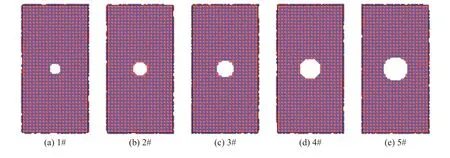
图12 不同孔洞尺寸的AlNi3模型切面图Fig.12 AlNi3 model section diagrams at different voids sizes
将5组模型沿Z轴匀速进行拉伸模拟,绘制不同孔洞尺寸的模型应力-应变曲线,如图13所示。从图中可以看出,5组模型在弹性变形阶段的曲线随孔洞尺寸增大略有降低,计算各对应的弹性模量,分别为219.611、218.178、216.097、213.775、210.071 GPa,即当预制孔洞半径从2.0a0增大至4.0a0时,其弹性模量由219.611 GPa减小到210.071 GPa,降低了4.34%;随着预制孔洞半径增加,5组AlNi3模型分别在应变为0.1096、0.1022、0.0942、0.0908、0.0844时,达到应力最大值,即抗拉强度依次为21.047、19.920、18.543、17.836、16.554 GPa。即当预制孔洞半径从2a0增大为4a0时,其抗拉强度下降了21.35%,拉伸应变下降了22.72%。结果表明,随着预制孔洞尺寸的增大,AlNi3模型拉伸应变和抗拉强度会明显降低,但对弹性模量影响较小。
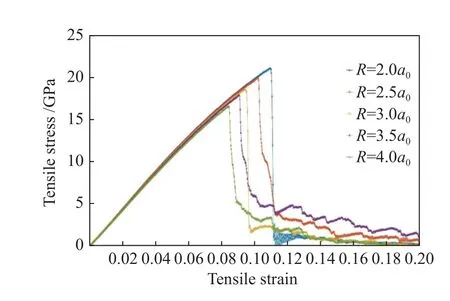
图13 不同孔洞尺寸的AlNi3模型应力-应变曲线图Fig.13 Stress-strain curves of AlNi3 models at different void sizes
2.2.3 不同预制孔洞数量的AlNi3拉伸结果分析
为了研究AlNi3模型拉伸力学性能是否与预制孔洞数量有关,设置预制孔洞数量为1、3、5、7共4组模型,孔洞半径均为R=2a0=0.7136 nm。4组模型预制孔洞具体参数如表2所示。图14为对应的AlNi3模型切面图。

表2 预制孔洞的模型具体参数Table 2 Model specific parameters of prefabricated voids
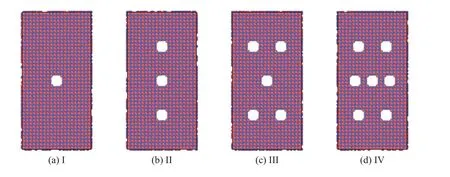
图14 不同孔洞数量的AlNi3模型切面图Fig.14 AlNi3 model section diagrams with different number of voids
将4组模型在300 K、NVT条件下沿Z轴匀速进行拉伸模拟,绘制不同孔洞数量的AlNi3模型应力-应变曲线,如图15所示。从图中可知:在弹性变形阶段,随着孔洞数量的增加,4条曲线有微小降低的趋势,对应的弹性模量分别为219.611、216.004、213.250、209.145 GPa,即当孔洞数量从1增加至7时,弹性模量降低了4.77%;预制孔洞数量为1、3、5、7时,分别在应变为0.1096、0.1132、0.1040、0.0880时,对应的抗拉强度为21.047、21.126、19.653、17.076 GPa,总体呈下降趋势,最小值比最大值降低了19.17%。
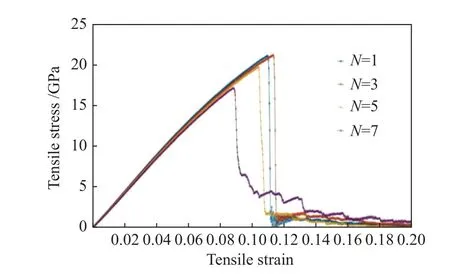
图15 不同孔洞个数AlNi3模型应力-应变图Fig.15 Stress-strain diagram of AlNi3 model with different number of voids
3 结论
1)在300 K条件下,当应变为0.1342时,AlNi3模型应力达到峰值23.397 GPa。温度增加会使AlNi3模型的弹性模量和抗拉强度减小。温度由300 K升高至900 K,其抗拉强度从23.397降低到17.573 GPa,降低了24.89%;应变速率的变化对弹性模量几乎没有影响,当应变速率从0.0002 ps-1升至0.0100 ps-1时,抗拉强度由23.397 GPa提高到24.669 GPa,增加应变速率会使抗拉强度有一定程度的升高。
2)在室温条件下,当应变为0.1096时,含预制孔洞AlNi3模型应力达到峰值21.047 GPa。孔洞半径从2a0增大为4a0,其抗拉强度会从21.047 GPa降低到16.554 GPa;预制孔洞数量从3个增加到7个,对应抗拉强度由21.126 GPa降低到17.076 GPa。增加孔洞半径或数量,会使模型弹性模量减小,抗拉强度也会降低。
