分数阶Mackey-Glass方程的分支和控制
2023-11-20乔宗敏
乔宗敏
(合肥师范学院 数学与统计学院,安徽 合肥 230601)
时滞微分方程是具有时间滞后的微分方程, 被用于描述既依赖于当前状态又依赖于过去状态的发展系统,能准确地刻画实际问题.在流体力学、种群生态学、经济学及现代控制理论等领域中存在着大量的时滞微分方程,故对时滞系统模型进行研究有着一定的现实意义.分数微积分是普通微积分的推广,在生物工程、电分析化学、粘弹性、热传导和经济学等领域中有着广泛的应用,因此对分数阶时滞微分方程的理论和应用的研究,也受到了学者们的更多关注[1-5].
Mackey-Glass时滞微分方程[6]
(1)
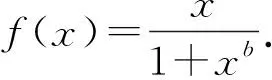
Famer[7]研究了Mackey-Glass方程的混沌性态, 当τ>17时,该方程表现出混沌性,正Lyapunov指数随着τ值的增加而增大,说明其混沌程度越来越高. Skubachevskii等[8]研究了方程(1)周期解的稳定性.Wei[9]利用全局Hopf分支理论,证明方程(1)Hopf分支的存在性.
论文研究分数阶Mackey-Glass微分方程
Dαx(t)=-cx(t)+af(x(t-τ)),
(2)
主要研究两个问题:(1)系统在时滞参数和分数阶导数的影响下Hopf分支的存在性;(2)在不稳定状态下,讨论非平凡平衡点控制策略.
1 预备知识
分数阶导数主要有3种:Riemann-Liouville,Grunwald-Letnikov和Caputo导数.论文采用Caputo导数的定义.
定义1Caputo导数[10]定义如下
Dαx(t)=Jm-αxm(t),α>0,
其中:m=[α]为第一个不大于α的整数;xm(t)为x(t)的m阶导数.
Jβ是β阶Riemann-Liouville积分算子,即
其中:Γ(·)是Gamma函数.
引理1[10]分数阶线性微分方程为
Dax(t)=Ax(t),x(0)=x0,
其中:x∈n;矩阵A∈n×n;0<αi<1,i=1,2,…,n是分数阶导数.则系统渐近稳定的充分必要条件是其中:λi是A的特征值.
引理2[11]设x(t)是上的可微函数,则对于所有t≥t0,有
Dαx2(t)≤2x(t)Dαx(t),∀α∈(0,1).
引理3[12-13]分数阶时滞微分方程

2 稳定性和Hopf分支分析
假设(H)a>c>0,b>0 ,则方程(2)具有唯一的正平衡点x0为
下面研究正平衡点的稳定性和局部Hopf分支的存在性,方程(2)的线性化方程为
Dαx(t)=-cx(t)+af′(x0)x(t-τ),
特征方程为
λα+c-af′(x0)e-λτ=0,
(3)
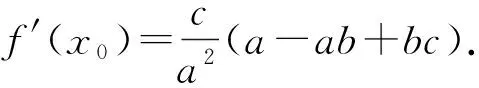
定理1对分数阶Mackey-Glass方程(2),以下结论成立:
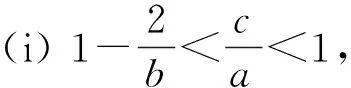

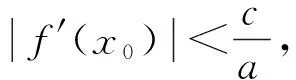
当τ>0时,如果iω(ω>0)是纯虚根,则由(3)得
分离实部和虚部得
(4)
两式平方相加得
解得
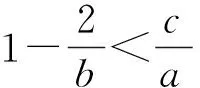
(5)
下面讨论系统在τ0的分叉情况.令λk(τ)是特征方程的特征根,满足λk(τk)=iω0.对(3)式两边关于τ求导,得
结合已知条件λα+c-af′(x0)e-λτ=0,得
将λk(τk)=iω0代入得
从而得到
因此横截条件成立,由Rouche’s定理和假设(H)知定理的结论(ii)成立.
3 平衡点的稳定控制
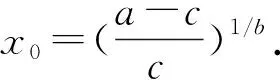
Dαy(t)=-cy(t)+a(f(y(t-τ)+x0)-f(x0)).
设g(y(t-τ))=f(y(t-τ)+x0)-f(x0),有
Dαy(t)=-cy(t)+ag(y(t-τ)).
为了将系统稳定控制在不稳定的平衡点x0,论文设计状态反馈控制器
Dαy(t)=-cy(t)+ag(y(t-τ))+u(t),
(6)
其中:u(t)=ky(t).控制参数k满足定理2,就可以实现分数阶Mackey-Glass方程(2)的稳定控制.
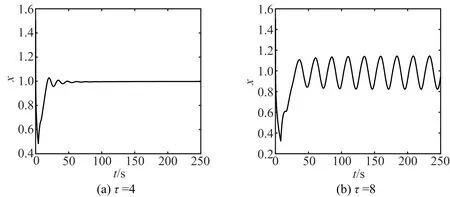
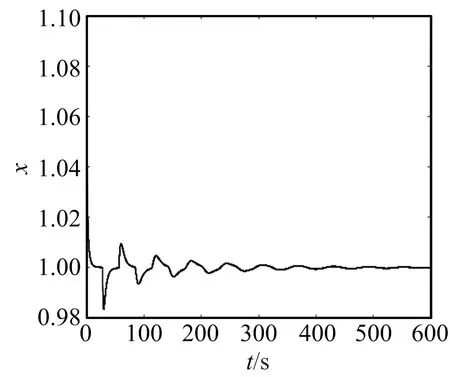
定理2当控制变量满足k g2(y(t-τ))=(f(y(t-τ)+x0)-f(x0))2≤|f′(ξ)|2y2(t-τ)≤y2(t-τ). DαV(t)≤yDαy≤y(t)(-cy(t)+ag(y(t-τ))+ky(t))= 分数阶时滞系统(1)具有唯一的正平衡x0,方程(1)表现出复杂的动力学行为,可能导致混沌现象的产生.在下面的数值模拟中分别取参数a=0.2,b=10,c=0.1,α=0.9,初值x0=1.5,系统唯一的正平衡x0=1,此时满足定理1的(ii).参数代入(4)中计算得ω0=0.333 3,τ0= 5.933 4,因此,当τ∈(0,τ0)时,正平衡点是渐近稳定的,而当τ∈(τ0,+∞)时,正平衡点不稳定,如图1所示.图1(a)中取τ=4<τ0,图1(b)中取τ=8>τ0,与定理1结果相符. 图1 分数阶Mackey-Glass方程的状态图 为了研究分数阶导数和时滞参数对分数阶Mackey-Glass方程(2)的影响,利用最值法做出了分数阶Mackey-Glass方程关于这两个参数的分叉图,如图2所示.图2(a)是方程关于分数阶导数的分叉图,参数选取为a=0.2,b=10,c=0.1,τ=28,当分数阶导数q>0.8时,方程(2)出现较复杂的现象.图2(b)是方程关于时滞变量的分叉图,参数选取为a=0.2,b=10,c=0.1,q=0.9,可以看出系统在τ0=5.933 4附近出现分叉,随着τ的增加,出现周期震荡,当τ>18时系统进入混沌状态.图2(c)中,选取分数阶导数q∈[0.5,1]和τ∈[0,25],可以观察方程分叉点的变化,随着分数阶导数q的增加,分叉点τ逐渐减小,从而方程(2)的稳定区域变小. 图2 分数阶Mackey-Glass方程的分叉及与时滞参数的关系图 在平衡点稳定控制的数值模拟中,参数选取为a=0.2,b=10,c=0.1,α=0.9,τ=28,如果取控制参数k=-0.35,k 图3 分数阶Mackey-Glass方程在控制参数k=-0.35作用下的状态图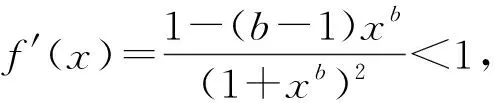
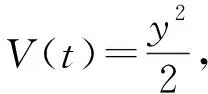
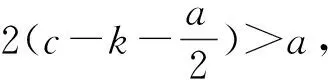
4 数值模拟

5 结 论