MTL代数的直觉模糊理想
2023-11-20刘春辉
刘春辉
(赤峰学院 教育科学学院,内蒙古 赤峰 024000)
对各种逻辑代数系统结构的研究是模糊逻辑及其应用研究的重要方向之一.Wang等[1]基于对模糊推理基础问题的深刻剖析,为模糊命题演算提出了一个形式系统L*,之后,又构建了与之相对应的R0代数.Hájek[2-3]针对由连续t-范数确定的模糊逻辑结构,提出了一个称之为基本逻辑的新的形式系统BL(basic logic),并提出了与之匹配的BL代数.Esteva等[4]提出了一个称之为Monoidalt-范基逻辑的形式系统MTL(monoidalt-norm basic logic),并提出了与之匹配的MTL代数.研究表明,系统L*是由幂零极小t-范数确定的模糊逻辑结构的共同形式化,系统BL是所有由连续t-范数确定的模糊逻辑结构的共同形式化,而系统MTL是所有由左连续t-范数确定的模糊逻辑结构的共同形式化,且系统L*和系统BL都是系统MTL的模式扩张.进一步地,R0代数和BL代数都是MTL代数的特殊子类[5-7].因此,对MTL代数结构的研究具有重要意义[8-9].
模糊集的概念是由美国著名控制论专家Zadeh在文献[10]中首次提出的,如今,模糊集理论已经在众多领域得到广泛应用[11].作为对Zadeh模糊集概念的一种推广,Atanassov[12]首次提出了直觉模糊集的概念.近年来,人们将直觉模糊集应用于群、环、域等抽象代数结构和多种逻辑代数结构问题的研究,获得了一批有理论价值和应用前景的研究成果[13-20].这些成果一方面丰富了代数理论的研究内容,另一方面也有效拓展了直觉模糊集的应用范围.受这些工作的启迪,考虑到理想概念在MTL代数结构刻画中的有效性,论文在MTL代数中将直觉模糊集与理想概念相结合,引入直觉模糊理想和直觉模糊素(Boolean/关联/超/固执)理想等概念并深入讨论它们的性质、刻画和相互关系,获得了一些有趣且有意义的结论.
1 预备知识
为了叙述简洁起见,该节给出关于MTL代数及直觉模糊集的一些基本概念和相关结论.
定义1[4](i) 称代数系统(L,≤,∧,∨,⊙,→,0,1)为剩余格,简称L为剩余格,如果下列各条成立:
(RL1) (L,∧,∨,0,1)是有界格;
(RL2) (L,⊙,1)是有单位元的交换半群;
(RL3) (⊙,→)是L上的伴随对,即(∀x,y,z∈L)(z≤x→y⟹x⊙z≤y).
(ii) 称剩余格L为MTL代数,如果L满足:(MTL1)(∀x,y∈L)((x→y)∨(y→x)=1).
引理1[4]设L是剩余格,定义L上运算*,使得∀x∈L,x*=x→0,则对任意的x,y,z∈L,有:
(RL4)x≤y⟹x→y=1;
(RL5) 1→x=x且y→(x→y)=1;
(RL6) 如果x≤y,那么z→x≤z→y且y→z≤x→z;
(RL7)x≤y→z⟹y≤x→z;
(RL8)x≤(x→y)→y且y≤(x→y)→y;
(RL9)x→(y→z)=y→(x→z)=x⊙y→z;
(RL10)z→y≤(x→z)→(x→y)且z→y≤(y→x)→(z→x);
(RL11)x→(y∧z)=(x→y)∧(x→z)且(y∨z)→x=(y→x)∧(z→x);
(RL12) ((x→y)→y)→y=x→y;
(RL13)x≤y⟹y*≤x*⟹x**≤y**;
(RL14)x≤x**且x***=x*,x→y≤y*→x*;
(RL15)x⊙y≤x∧y且x⊙x*=0;
(RL16) (x∨y)*=x*∧y*;
(RL17)x⊙(x→y)≤y且x≤x*→y;
(RL18) (x→y*)**=x→y*=y→x*=(x⊙y)*.
引理2[8]设L是MTL代数,则对任意的x,y,z∈X,有:
(MTL2)x≤y⟹x⊙z≤y⊙z;
(MTL3)y→z≤x∨y→x∨z;
(MTL4) (x∧y)*=x*∨y*;
(MTL5)x∨y=((x→y)→y)∧((y→x)→x);
(MTL6) (x∧y)→z=(x→z)∨(y→z)且x→(y∨z)=(x→y)∨(x→z);
(MTL7)x∧(y∨z)=(x∧y)∨(x∧z)且x∨(y∧z)=(x∨y)∧(x∨z).
定义2[9]设L是MTL代数,∅≠I⊆L.称I是L的一个理想,如果I满足:
(Id1) 0∈I;
(Id2) 对任意的x,y∈L,x∈I且(x*→y*)*∈I蕴涵y∈I.
定义3[9]设L是MTL代数,I是L的一个理想,有:
(i) 对任意x∈L,若x∧x*∈I,则称I是L的一个Boolean理想;
(ii) 对任意x,y∈L,若(x→(y→x)*)*∈I蕴涵x∈I,则称I是L的一个关联理想;
(iii) 对任意x,y∈L,若x∧y∈I蕴涵x∈I或x∈I,则称I是L的一个素理想;
(iv) 对任意x∈L,若x∈I或x*∈I,则称I是L的一个超理想;
(v) 对任意x,y∈L,若x∉I且y∉I蕴涵(x→y)*∈I且(y→x)*∈I,则称I是L的固执理想.
定义4[10]设X是一个非空集合,则X上的一个模糊集指的是映射f:X→[0,1]. 设f是X上的一个模糊集,对任意的t∈[0,1],称集合ft={x∈X|f(x)≥t}为f的t-截集.
为叙述方便,对任意的a,b∈[0,1],分别用a∧b和a∨b表示min(a,b)和max(a,b).
定义5[11]设L是MTL代数,f是X上的一个模糊集,如果f满足:对任意的x,y∈X,有:
(FI1)f(0)≥f(x);
(FI2)f(y)≥f(x)∧f((x*→y*)*).
则称f是X的一个模糊理想.
引理3[11]设L是MTL代数,则X上的模糊集f是X的一个模糊理想当且仅当f满足
(FI3) 对任意的t∈[0,1],ft≠∅⟹ft是L的理想.
定义6[12]设U是一个给定论域,则U上的一个直觉模糊集A定义为
A={〈x,μA(x),νA(x)〉|x∈U},
其中:μA:U→[0,1]和νA:U→[0,1]是U上的两个模糊集,分别代表A的隶属函数和非隶属函数,且对任意的x∈U,0≤μA(x)+νA(x)≤1.集合U上的直觉模糊集的全体之集记为IFS(U).
定义7[12]设U是一个给定论域,A∈IFS(U). 称A是U上的常值直觉模糊集,如果对任意的x∈U,μA(x)=s且νA(x)=t,s,t∈[0,1]且0≤s+t≤1.
2 MTL代数的直觉模糊理想与直觉模糊格理想
该节引入MTL代数的直觉模糊理想概念,并考察其性质及其与直觉模糊格理想的关系.
定义8设L是MTL代数,A∈IFS(L). 称A是L的一个直觉模糊理想,如果A满足:∀x,y∈L,有:
(IFI1)μA(0)≥μA(x)且νA(0)≤νA(x);
(IFI2)μA(y)≥μA(x)∧μA((x*→y*)*)且νA(y)≤νA(x)∨νA((x*→y*)*).
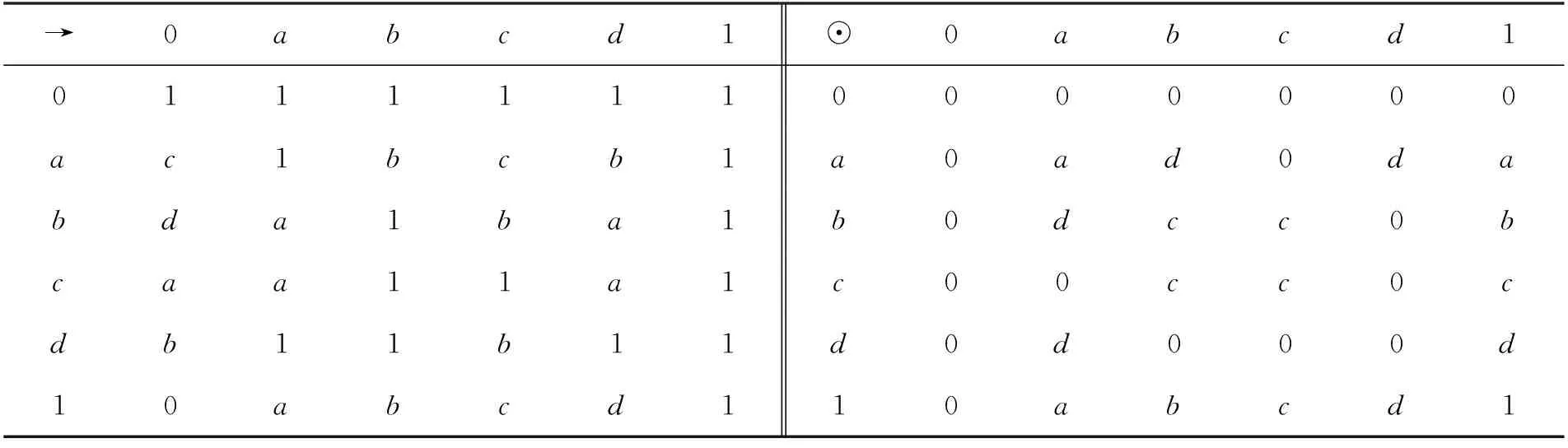
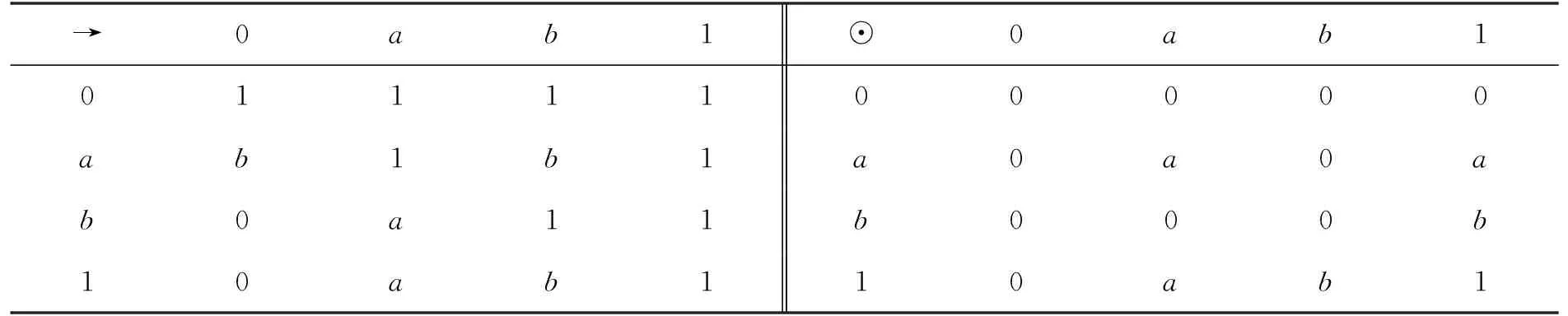
例1设L={0,a,b,1}且0 表1 例1中L上二元运算“→”和“⊙”的定义 且∀x∈L,x*=x→0. 可以验证(L,≤,∧,∨,⊙,→,0,1)是一个MTL代数. 定义A∈IFS(L)满足 则A是L的一个直觉模糊理想. 定理1设L是MTL代数,A是L的一个直觉模糊理想,则下列各条成立:∀x,y∈L,有: (IFI3) (μA((x*→y*)*)=μA(0)且νA((x*→y*)*)=νA(0))⟹(μA(x)≤μA(y),νA(x)≥νA(y)); (IFI4)x*≤y*⟹(μA(x)≤μA(y)且νA(x)≥νA(y)); (IFI5)x≤y⟹(μA(y)≤μA(x)且νA(y)≥νA(x)); (IFI6)μA(x)=μA(x**)且νA(x)=νA(x**). 证明(1) 对任意的x,y∈L,设μA((x*→y*)*)=μA(0)且νA((x*→y*)*)=νA(0). 因为A是L的一个直觉模糊理想,所以由(IFI2)和(IFI1)得 μA(y)≥μA(x)∧μA((x*→y*)*)=μA(x)∧μA(0)=μA(x), νA(y)≤νA(x)∨νA((x*→y*)*)=νA(x)∨νA(0)=νA(x), 因此(IFI3)成立. (2) 对任意的x,y∈L,设x*≤y*,则由(RL4)得(x*→y*)*=1*=0,所以 μA((x*→y*)*)=μA(0)且νA((x*→y*)*)=νA(0), 故由(IFI3)得μA(x)≤μA(y)且νA(x)≥νA(y),即(IFI4)成立. (3) 对任意的x,y∈L,设x≤y,则由(RL13)得y*≤x*,由(IFI4)得μA(y)≤μA(x)且νA(y)≥νA(x),因此(IFI5)成立. (4) 对任意的x∈L,一方面,因为x≤x**,所以由(IFI5)得μA(x**)≤μA(x)且νA(x**)≥νA(x).另一方面,由(IFI2),(RL4)和(IFI1)得 μA(x**)≥μA(x)∧μA((x*→x***)*)= μA(x)∧μA((x*→x*)*)=μA(x)∧μA(1*)=μA(x)∧μA(0)=μA(x), νA(x**)≤νA(x)∨νA((x*→x***)*)= νA(x)∨νA((x*→x*)*)=νA(x)∨νA(1*)=νA(x)∨νA(0)=νA(x), 因此,综合两方面得μA(x)=μA(x**)且νA(x)=νA(x**),即(IFI6)成立. 定理2设L是MTL代数,A∈IFS(L),则对任意的x,y,z∈L,A是L的直觉模糊理想当且仅当如下二条件之一成立: (IFI7)z*⊙y*≤x*⟹(μA(x)≥μA(y)∧μA(z)且νA(x)≤νA(y)∨νA(z)); (IFI8)z*→(y*→x*)=1⟹(μA(x)≥μA(y)∧μA(z)且νA(x)≤νA(y)∨νA(z)). 证明设A是L的一个直觉模糊理想且对任意的x,y,z∈L,z*⊙y*≤x*,则由(RL3)和(RL18)得z*≤y*→x*=(y*→x*)**.由(IFI4)得μA(z)≤μA((y*→x*)*)且νA(z)≥νA((y*→x*)*). 由(IFI2)得μA(x)≥μA(y)∧μA((y*→x*)*)≥μA(y)∧μA(z)且νA(x)≤νA(y)∨νA((y*→x*)*)≤νA(y)∨νA(z),即(IFI7)成立. 反之,设(IFI7)成立,因为对任意的x∈L,x*⊙x*≤1=0*,所以由(IFI7)得 μA(0)≥μA(x)∧μA(x)=μA(x)且νA(0)≤νA(x)∨νA(x)=νA(x), 故A满足(IFI1).又因为对任意的x,y∈L,由(RL18)和(RL17)得 (x*→y*)**⊙x*=x*⊙(x*→y*)≤y*, 所以由(IFI7)有μA(y)≥μA(x)∧μA((x*→y*)*)且νA(y)≤νA(x)∨νA((x*→y*)*),即A亦满足(IFI2).因此,由定义8得A是L的一个直觉模糊理想. 对任意的x,y∈L,由(RL3)和(RL4)显然可得z*⊙y*≤x*⟺z*→(y*→x*)=1,从而得(IFI7)与(IFI8)等价. 定理得证. 证明“必要性”.设A是L的直觉模糊理想,则由定义5,8,显然μA是L的模糊理想. 任取x,y∈L,因为由(IFI1)和(IFI2)知νA(0)≤νA(x)且νA(y)≤νA(x)∨νA((x*→y*)*),所以 (1-νA(x))∧(1-νA((x*→y*)*))=1-νA(x)∨νA((x*→y*)*), 即νA(y)≤νA(x)∨νA((x*→y*)*).因此,由定义8得A是L的直觉模糊理想. 证明由引理3和定理3立即可得. 定义9设L是MTL代数,A∈IFS(L). 称A是L的直觉模糊格理想,如果对任意的x,y∈L,A满足(IFI5)和如下的(IFI9) (IFI9)μA(x∨y)≥μA(x)∧μA(y)且νA(x∨y)≤νA(x)∨νA(y). 定理4设L是MTL代数,则L的任一直觉模糊理想都是L的直觉模糊格理想. 证明设A是L的直觉模糊理想,则由定理1知A满足(IFI5). 下证A满足(IFI9).事实上,对任意的x,y∈L,因为由(RL9)和(RL5)得y*→(x*→y*)=x*→(y*→y*)=x*→1=1,所以由(RL4)得y*≤x*→y*,从而由(RL13)得(x*→y*)*≤y**,进而由(IFI5)和(IFI6)得 μA((x*→y*)*)≥μA(y**)=μA(y)且νA((x*→y*)*)≤νA(y**)=νA(y). 由 (RL16)和(RL11)得 (x*→(x∨y)*)*=(x*→(x*∧y*))*=((x*→x*)∧(x*→y*))*= (1∧(x*→y*))*=(x*→y*)*, 所以再由(IFI2)得 μA(x∨y)≥μA(x)∧μA((x*→(x∨y)*)*)=μA(x)∧μA((x*→y*)*)≥μA(x)∧μA(y), νA(x∨y)≤νA(x)∨νA((x*→(x∨y)*)*)≤νA(x)∨νA((x*→y*)*)≤νA(x)∨νA(y), 因此,由定义9得A是L的直觉模糊格理想. 注1定理9的逆命题一般不真,即MTL代数直觉模糊格理想不必为直觉模糊理想. 例2设L={0,a,b,c,d,1}且其Hasse图如图1所示,定义L上二元运算“→”和“⊙”如表2所示. 图1 格L的Hasse图 表2 例2中L上二元运算“→”和“⊙”的定义 且∀x∈L,x*=x→0. 可以验证(L,≤,∧,∨,⊙,→,0,1)是一个MTL代数. 定义A∈IFS(L)满足 则A是L的一个直觉模糊格理想.但A不是L的一个直觉模糊理想,因为 μA(a)=0.2<0.7=μA(d)∧μA((d*→a*)*). 该节在MTL代数中引入直觉模糊Boolean理想、直觉模糊素理想、直觉模糊超理想和直觉模糊固执理想等多种特殊类型理想概念,并讨论其性质和相互关系. 定义10设L是MTL代数,称L的直觉模糊理想A是直觉模糊Boolean理想,若A满足:∀x∈L,有 (IFI10)μA(x∧x*)=μA(0)且νA(x∧x*)=νA(0). 例3设L={0,a,b,1}且0 表3 例3中L上二元运算“→”和“⊙”的定义 且∀x∈L,x*=x→0,可以验证(L,≤,∧,∨,⊙,→,0,1)是一个MTL代数. 定义A∈IFS(L)满足 则A是L的一个直觉模糊Boolean理想. 注2MTL代数的直觉模糊理想不必是直觉模糊Boolean理想. 如例1中所给MTL代数L的直觉模糊理想A不是L的直觉模糊Boolean理想,这是因为 μA(a∧a*)=μA(a∧a)=μA(a)=0.3≠0.7=μA(0). 定理5设L是MTL代数,A是L的直觉模糊Boolean理想,则对任意的x∈X,如下结论成立 (IFI11)μA(x)≥μA((x→x*)*)且νA(x)≤νA((x→x*)*). 证明设A是L的直觉模糊Boolean理想,则∀x∈X,μA(x∧x*)=μA(0)且νA(x∧x*)=νA(0). 因为 ((x∧x*)*→x*)*=(x→(x∧x*)**)*=(x→(x*∨x**)*)*=(x→(x**∧x***))*= ((x→x**)∧(x→x***))*=(1∧(x→x*))*=(x→x*)*, 所以由(IFI1)和(IFI2),得 μA(x)≥μA(x∧x*)∧μA(((x∧x*)*→x*)*)μA(0)∧μA((x→x*)*)=μA((x→x*)*), νA(x)≤νA(x∧x*)∨νA(((x∧x*)*→x*)*)=νA(0)∨νA((x→x*)*)=νA((x→x*)*), 因此,A满足(IFI11). 定义11设L是MTL代数,称L的直觉模糊理想A是直觉模糊关联理想,若A满足:∀x,y∈L,有 (IFI12)μA(x)≥μA((x→(y→x)*)*)且νA(x)≤νA((x→(y→x)*)*). 定理6设L是MTL代数,A∈IFS(L),则A是L的直觉模糊Boolean理想当且仅当A是L的直觉模糊关联理想. 证明“必要性”.设A是L的直觉模糊Boolean理想. 对任意的x,y∈L,因为 ((x→(y→x)*)**→(x→x*)**)*=((x→x*)*→(x→(y→x)*)***)*= ((x→x*)*→(x→(y→x)*)*)*≤((x→(y→x)*)→(x→x*))*≤ ((y→x)*→x*)*≤(x→(y→x))*=1*=0, 所以((x→(y→x)*)**→(x→x*)**)*=0. 故由(IFI11),(IFI1)和(IFI2),得 μA(x)≥μA((x→x*)*)≥μA((x→(y→x)*)*)∧ μA(((x→(y→x)*)**→(x→x*)**)*)= μA((x→(y→x)*)*)∧μA(0)=μA((x→(y→x)*)*), νA(x)≤νA((x→x*)*)≤νA((x→(y→x)*)*)∨ νA(((x→(y→x)*)**→(x→x*)**)*)= νA((x→(y→x)*)*)∨νA(0)=νA((x→(y→x)*)*), 即A满足(IFI12).因此,由定义11知A是L的直觉模糊Boolean理想. “充分性”.设A是L的直觉模糊关联理想,对任意的x∈L,因为 ((x∧x*)→(1→(x∧x*))*)*=((x∧x*)→(x∧x*)*)*= ((x∧x*)→(x*∨x**))*=(((x∧x*)→x*)∨((x∧x*)→x**))*= (1∨((x∧x*)→x**))*=1*=0, 所以再由(IFI12),得 μA(x∧x*)≥μA(((x∧x*)→(1→(x∧x*))*)*)=μA(0), νA(x∧x*)≤νA(((x∧x*)→(1→(x∧x*))*)*)=νA(0), 又由(IFI1)得μA(x∧x*)≤μA(0)且νA(x∧x*)≥νA(0),所以,得 μA(x∧x*)=μA(0)且νA(x∧x*)=νA(0), 即A满足(IFI10).因此,由定义10知A是L的直觉模糊Boolean理想. 定义12设L是MTL代数,称L的非常值直觉模糊理想A是直觉模糊素理想,若A满足:∀x,y∈L,有 (IFI13)μA(x∧y)≤μA(x)∨μA(y)且νA(x∧y)≥νA(x)∧νA(y). 例4(i) 设L是例3中所给MTL代数,定义A∈IFS(L)满足 则A是L的一个直觉模糊素理想. (ii) 设L={0,a,b,1}且其Hasse图如图2所示,定义L上二元运算“→”和“⊙”如表4所示. 图2 格L的Hasse图 表4 例4中L上二元运算“→”和“⊙”的定义 且∀x∈L,x*=x→0, 可以验证(L,≤,∧,∨,⊙,→,0,1)是一个MTL代数. 定义A∈IFS(L)满足 则A是L的一个直觉模糊理想.但A不是L的一个直觉模糊素理想,因为 μA(a∧b)=0.9>0.2=μA(a)∨μA(b). 定理7设L是MTL代数,则L的非常值直觉模糊理想A是直觉模糊素理想当且仅当A满足:∀x,y∈L,有 (IFI14) (μA(x∧y)=μA(0)且νA(x∧y)=νA(0))⟹((μA(x)=μA(0),νA(x)=νA(0))或(μA(y)=μA(0),νA(y)=νA(0))). 证明“必要性”.设A是L的直觉模糊素理想,对任意的x,y∈X,μA(x∧y)=μA(0)且νA(x∧y)=νA(0),则由(IFI13)得μA(0)=μA(x∧y)≤μA(x)∨μA(y)且νA(0)=νA(x∧y)≥νA(x)∧νA(y),而由(IFI1)得μA(x∧y)≤μA(0)且νA(x∧y)≥νA(0),故μA(x∧y)=μA(0)且νA(x∧y)=νA(0).注意到A是直觉模糊理想,得μA(x)=μA(0),νA(x)=νA(0)或μA(y)=μA(0),νA(y)=νA(0),即(IFI14)成立. “充分性”.设A是L的非常值直觉模糊理想且满足(IFI14). 假设A不满足(IFI13),则存在x0,y0∈L,使得μA(x0∧y0)>μA(x0)∨μA(y0)或νA(x0∧y0)<νA(x0)∧νA(y0). 此时,若μA(x0∧y0)=μA(0)且νA(x0∧y0)=νA(0),则μA(0)>μA(x0)∨μA(y0)或νA(0)<νA(x0)∧νA(y0),从而μA(x0)<μA(0)且μA(y0)<μA(0),或νA(x0)>νA(0)且νA(y0)>νA(0),这与(IFI14)矛盾,因此,A满足(IFI13),即A是L的直觉模糊素理想. 定理8设L是MTL代数,则L的非常值直觉模糊理想A是直觉模糊素理想当且仅当A满足:∀x,y∈L,有 (IFI15) (μA((x→y)*)=μA(0),νA((x→y)*)=νA(0)), 或 (μA((y→x)*)=μA(0),νA((y→x)*)=νA(0)). 证明“必要性”.设A是L的直觉模糊素理想,对任意的x,y∈L,由(RL16)和(MTL1),得 (x→y)*∧(y→x)*=((x→y)∨(y→x))*=1*=0, 所以μA((x→y)*∧(y→x)*)=μA(0)且νA((x→y)*∧(y→x)*)=νA(0),从而由(IFI14),得 μA((x→y)*)=μA(0),νA((x→y)*)=νA(0)或 μA((y→x)*)=μA(0),νA((y→x)*)=νA(0), 即A满足(IFI15). “充分性”.设A是L的非常值直觉模糊理想且满足(IFI15). 对任意的x,y∈L,有 μA((x→y)*)=μA(0),νA((x→y)*)=νA(0), 或 μA((y→x)*)=μA(0),νA((y→x)*)=νA(0), 如果μA((x→y)*)=μA(0),νA((x→y)*)=νA(0),因为 ((x∧y)*→x*)*=((x*∨y*)→x*)*=((x*→x*)∧(y*→x*))*= (1∧(y*→x*))*=(y*→x*)*≤(x→y)*, 所以由(IFI5)得μA(((x∧y)*→x*)*)≥μA((x→y)*)且νA(((x∧y)*→x*)*)≤νA((x→y)*),有 μA(x)≥μA(x∧y)∧μA(((x∧y)*→x*)*)≥μA(x∧y)∧μA((x→y)*)= μA(x∧y)∧μA(0)=μA(x∧y), νA(x)≤νA(x∧y)∨νA(((x∧y)*→x*)*)=νA(x∧y)∨νA((x→y)*)= νA(x∧y)∨νA(0)=νA(x∧y). 如果μA((y→x)*)=μA(0),νA((y→x)*)=νA(0),类似可证μA(y)≥μA(x∧y)且νA(x)≤νA(x∧y).综合得μA(x∧y)≤μA(x)∨μA(y)且νA(x∧y)≥νA(x)∧νA(y),即A满足(IFI13),从而由定义12得A是L的直觉模糊素理想. 定义13设L是MTL代数,称L的非常值直觉模糊理想A是直觉模糊超理想,若A满足:∀x∈L,有 (IFI16) (μA(x)=μA(0),νA(x)=νA(0))或(μA(x*)=μA(0),νA(x*)=νA(0)). 例5(i) 设L是例2中所给MTL代数,定义A∈IFS(L)满足 则A是L的一个直觉模糊超理想. (ii) 例4(ii)中所给MTL代数L的直觉模糊理想A也不是L的直觉模糊超理想. 定理9设L是MTL代数,A是L的非常值直觉模糊集,则A是L的直觉模糊超理想当且仅当A既是直觉模糊素理想又是直觉模糊Boolean理想. 证明“必要性”.设A是L的直觉模糊超理想,则对任意的x∈L,μA(x)=μA(0),νA(x)=νA(0)或μA(x*)=μA(0),νA(x*)=νA(0). 首先,证明A是L的直觉模糊素理想.事实上,对任意的x,y∈L,设μA(x∧y)=μA(0)且νA(x∧y)=νA(0),如果μA(x)≠μA(0)且νA(x)≠νA(0),则由假设和(IFI16)得μA(x*)=μA(0)且νA(x*)=νA(0). 因为 ((x∧y)*→y*)*=((x*∨y*)→y*)*=((x*→y*)∧(y*→y*))*= ((y*→x*)∧1)*=(y*→x*)*≤(x→y)*≤x*, 所以由(IFI5)得μA(((x∧y)*→y*)*)≥μA(x*)=μA(0)且νA(((x∧y)*→y*)*)≤νA(x*)=νA(0),从而由(IFI1)得μA(((x∧y)*→y*)*)=μA(0)且νA(((x∧y)*→y*)*)=νA(0). 故由(IFI1)和(IFI2),得 μA(0)≥μA(y)≥μA(x∧y)∧μA(((x∧y)*→y*)*)=μA(0)∧μA(0)=μA(0), νA(0)≤νA(y)≤νA(x∧y)∨νA(((x∧y)*→y*)*)=νA(0)∨νA(0)=νA(0), 故由定理7得A是L的直觉模糊素理想. 其次,证明A是L的直觉模糊Boolean理想. 事实上,对任意的x∈L,因为x∧x*≤x且x∧x*≤x*,所以由(IFI5)得μA(x∧x*)≥μA(x),νA(x∧x*)≤νA(x)且μA(x∧x*)≥μA(x*),νA(x∧x*)≤νA(x*). 由假设及(IFI16)知μA(x)=μA(0),νA(x)=νA(0)或μA(x*)=μA(0),νA(x*)=νA(0),所以μA(x∧x*)≥μA(0)且νA(x∧x*)≤νA(0),故再结合(IFI1)得μA(x∧x*)=μA(0)且νA(x∧x*)=νA(0),即A满足(IFI10),故A是L的直觉模糊Boolean理想. “充分性”.设A既是L的直觉模糊素理想又是直觉模糊Boolean理想.对任意的x∈X,由A是L的直觉模糊Boolean理想及(IFI10)得μA(x∧x*)=μA(0)且νA(x∧x*)=νA(0),从而再由A是L的直觉模糊素理想及(IFI14)得μA(x)=μA(0),νA(x)=νA(0)或μA(x*)=μA(0),νA(x*)=νA(0),即A满足(IFI16).因此,A是L的直觉模糊超理想. 定理10设L是MTL代数,A是L的非常值直觉模糊集,则A是L的直觉模糊超理想当且仅当A既是直觉模糊素理想又是直觉模糊关联理想. 证明由定理6,9立即可得. 定义14设L是MTL代数,称L的非常值直觉模糊理想A是L的直觉模糊固执理想,如果A满足:∀x,y∈L,有 (IFI17) (μA(x)≠μA(0),νA(x)≠νA(0)且μA(y)≠μA(0),νA(y)≠νA(0))⟹ (μA((x→y)*)=μA(0),νA((x→y)*)=νA(0), μA((y→x)*)=μA(0),νA((y→x)*)=νA(0)). 定理11设L是MTL代数,A是L的非常值直觉模糊集,则A是L的直觉模糊超理想当且仅当A是L的直觉模糊固执理想. 证明设A是L的直觉模糊超理想.对任意的x,y∈L,设μA(x)≠μA(0),νA(x)≠νA(0)且μA(y)≠μA(0),νA(y)≠νA(0),则由(IFI16)得μA(x*)=μA(0),νA(x*)=νA(0)且μA(y*)=μA(0),νA(y*)=νA(0). 因为 (x**→(y→x)**)*=((y→x)*→x***)*=((y→x)*→x*)*= (x→(y→x))*=1*=0, 所以(x**→(y→x)**)*=0,从而μA((x**→(y→x)**)*)=μA(0)且νA((x**→(y→x)**)*)=νA(0).故由(IFI2)及μA(x*)=μA(0),νA(x*)=νA(0),得 μA((y→x)*)≥μA(x*)∧μA((x**→(y→x)**)*)=μA(0)∧μA(0)=μA(0), νA((y→x)*)≤νA(x*)∨νA((x**→(y→x)**)*)=νA(0)∨νA(0)=νA(0). 结合(IFI1),得μA((y→x)*)=μA(0)且νA((y→x)*)=νA(0). 类似地,由μA(y*)=μA(0),νA(y*)=νA(0)可证μA((x→y)*)=μA(0)且νA((x→y)*)=νA(0),故A满足(IFI17),因此A是L的直觉模糊固执理想. 反之,设A是L的直觉模糊固执理想,且对任意的x∈L,μA(x)≠μA(0)且νA(x)≠νA(0).因为A是L的非常值直觉模糊集,所以μA(1)≠μA(0)且νA(1)≠νA(0),故由(IFI17)得 μA(x*)=μA(1→x*)=μA(0)且νA(x*)=νA(1→x*)=νA(0), 即A满足(IFI16),因此,A是L的直觉模糊超理想. 定理12设L是MTL代数,A是L的非常值直觉模糊集,则A是L的直觉模糊固执理想当且仅当A既是直觉模糊素理想又是直觉模糊Boolean(关联)理想. 证明由定理9,10,11立即可得. 论文在MTL代数框架下,将理想与直觉模糊集概念相结合,引入直觉模糊理想的概念并深入讨论了多种特殊类型的直觉模糊理想的性质和相互关系,这些工作有助于进一步深入理解和把握MTL代数的结构特征,为在非对合逻辑代数框架下开展针对理想及其相关问题的研究提供思想和方法上的借鉴.最后,为直观起见,作者将MTL代数的上述多种特殊类型直觉模糊理想间的相互关系总结如图3所示. 图3 多种特殊类型直觉模糊理想间的相互关系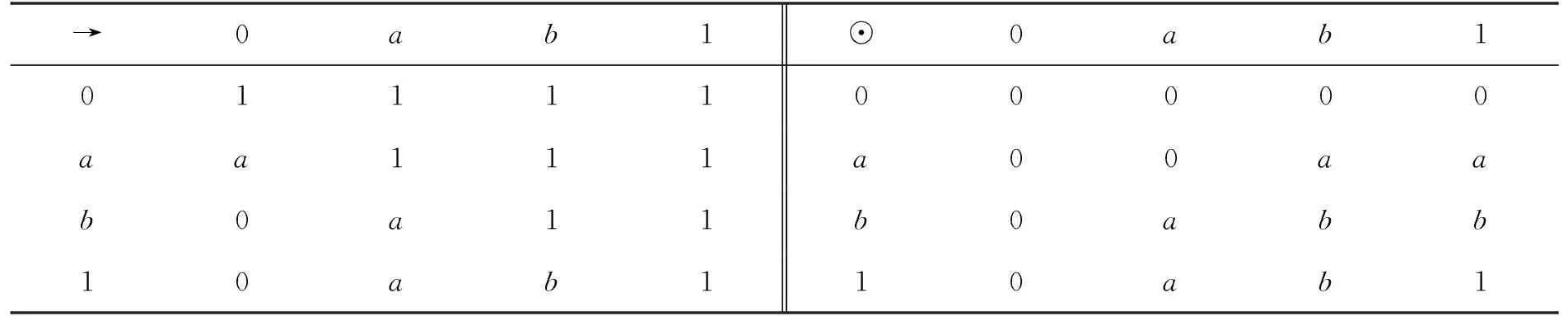




3 MTL代数的多种特殊类型直觉模糊理想及相互关系


4 结论与展望