面向暂态电压主动支撑的多功能并网变流器多模式柔性切换策略

2023-11-20贾文慧涂春鸣侯玉超黄泽钧

电力系统自动化 2023年21期

郭祺，贾文慧，涂春鸣，侯玉超，黄泽钧，姜飞

（1.国家电能变换与控制工程技术研究中心（湖南大学）,湖南省长沙市 410082；2.国网山西省电力公司晋中供电公司,山西省晋中市 030600；3.长沙理工大学电气与信息工程学院,湖南省长沙市 410004）

0 引言

随着国家“碳达峰·碳中和”目标的制定,国内新能源领域得到进一步推进与发展。但随着可再生能源与电力电子装置渗透率的增高,电网中电能质量问题如电压闪变、波动以及无功缺额等日益严峻［1-2］,在此背景下,电网的高质、高效、高可靠供电问题值得持续关注与突破［3-4］。

为满足新形势下高供电品质的需求,电力电子型电能质量治理装置凭借其智能性、灵活性的优势得到广泛推广和应用［5］。其中,基于并网变流器的电能质量治理装置如有源电力滤波器、无功补偿器等在谐波抑制、无功补偿等方面表现优异,且设备可靠性高,在电网故障时可以直接脱网运行。但并联接入电网的方式使得此类装置缺乏解决电压暂降/抬升等电压质量问题的能力［6-7］。

为此,目前主要有两种研究思路来进一步提高并联型电能质量治理装置的功能区间以及利用率。一是将并联型电能质量治理装置与串联变流器联合运行［8-9］,如统一电能质量调节器（unified power quality conditioner,UPQC）,其串联变流器可以解决电压质量问题,而并联侧解决电流质量问题［10-11］。目前,国内外研究学者对UPQC 的拓扑结构［12-13］以及控制策略［14-15］等方面开展了深入研究,但是UPQC 需要两套变流器,成本较高［16］。并联型动态电压恢复器不仅能实现电流补偿也可以治理电压波动,但现有方案需要两套变换器,增加了装置容量和成本,或在电压跌落程度较深时需由变换器补偿所有功率,对直流侧储能容量要求较高［17］。二是在一套变流器的基础上增加多组继电器/物理开关,实现硬投切,如现有串并联变流器一体化的方案［18-19］。其工作原理是通过多组开关的投切将变流器从并联入网方式强行切换至串联入网方式,进而实现电压补偿的目的。但是多组开关的投切导致负载侧可能存在短时断电的过程,暂态问题突出。此外,变流器在电压补偿期间直接串联接入电网,整体运行可靠性较低［20］。因此,并网变流器的高性能、低成本、高可靠问题值得进一步研究与探索。

基于此,本文提出一种以并联形式接入电网且能够灵活治理电网电流和电压质量问题的多功能并网变流器（multi-functional grid-connected converter,MF-GCC）拓扑结构及其多模式综合控制策略。首先,介绍了MF-GCC 的拓扑结构和工作原理。在电网电压正常时,MF-GCC 工作于并联补偿模式,动态补偿负载所需无功功率,实现网侧单位功率因数运行；在电网电压波动时,MF-GCC 工作于串联补偿模式,其通过补偿电压以维持负载电压幅值恒定。然后,详细分析开关导通时序与变流器有源部分不同模式控制指令配合切换下各种暂态电气量的变化规律,从而确定元部件动作逻辑,保证切换过程中瞬时电压、电流冲击最小以及模式间的平滑、快速切换。其次,总结了MF-GCC 的综合控制策略以及柔性切换策略。最后,通过仿真和实验,验证了所提柔性切换策略的有效性和可行性。

1 拓扑结构与工作原理

1.1 拓扑结构

本文所提MF-GCC 的拓扑结构如图1 所示,其由有源部分、多绕组变压器T、耦合电容C0、电阻Rn、变压器旁路开关S1和切换开关S2组成。有源部分包含LC 滤波环节（滤波电容C1与滤波电感L1）、单相全桥变换器和直流侧电容Cdc（直流侧储能元件可根据实际应用场景的电压质量问题与负荷侧需求因情况而定）。多绕组变压器的一次侧与输电线路连接,二次侧端口接入变流器,三次侧端口通过耦合电容C0接地,二、三次侧的公共端口通过开关S2和电阻Rn接地。图中:Udc为直流侧电压；U̇S、İS分别为电网电压、电流；İL1、İC1分别为滤波电感、滤波电容支路电流；U̇C1、İ1分别为MF-GCC 有源部分输出电压、电流；U̇C0为耦合电容C0两端电压；U̇R为电阻Rn两端电压；U̇tr、U̇tr1、U̇tr2分别为多绕组变压器一次、二次、三次侧电压；İnn为S2支路电流；İS1为S1支路电流；İcn为耦合电容支路电流；Z为线路阻抗；U̇L、İL分别为负载电压、电流；ZL为负载阻抗。

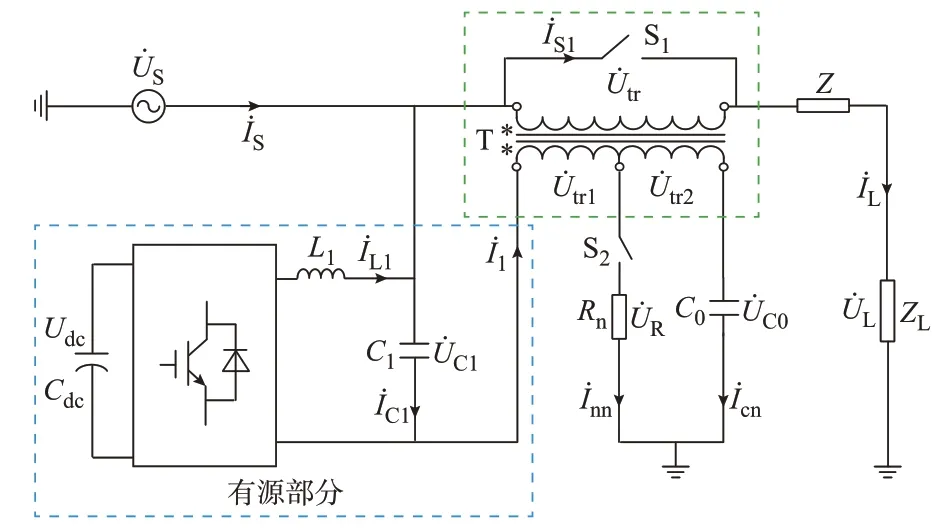
图1 MF-GCC 的拓扑结构Fig.1 Topology of MF-GCC

1.2 工作原理

根据电网的运行状态,MF-GCC 可工作于串联补偿模式和并联补偿模式两种模式。在电网电压处在波动（如跌落、抬升）状态时,MF-GCC 工作在串联补偿模式,通过向电网注入相应补偿电压来实现负载侧电压幅值不受网侧扰动的影响。当电网电压处在正常状态时,MF-GCC 工作在并联补偿模式,可向负荷侧提供无功功率。

1.2.1 串联补偿模式

1）基本工作原理

在电网电压处在波动的状态时,开关S1断开、开关S2闭合,MF-GCC 工作于串联补偿模式,如图2（a）所示。为使负载侧的电压幅值不受网侧干扰,可以控制U̇C1与U̇S的矢量差维持负载电压幅值恒定,如图2（b）和（c）所示,图中补偿后U̇L的相角为α。

图2 MF-GCC 在串联补偿模式下的拓扑及其电气量之间的相量关系Fig.2 Topology of MF-GCC in series compensation mode and phasor relationship between electrical quantities

所提变流器在串联补偿模式下的等效电路如附录A 图A1 所示。图中:变压器一次侧、二次侧、三次侧漏感分别为L1σ、L2σ、L3σ；变压器的励磁阻抗为Zm。所提变流器的有源部分在串联模式下相当于一个受控电压源。

假设变压器一次与二、三次侧绕组的匝数比为1∶1∶1,根据基尔霍夫电压定律（KVL）、基尔霍夫电流定律（KCL）可得MF-GCC 拓扑结构中电压、电流关系满足:

由于Rn数值较小,U̇R≈0,结合式（1）可得:

另外,由理想变压器特性可知变压器一次侧、二次侧、三次侧的电压关系为:

结合变压器匝数比为1∶1∶1,进一步得到:

根据式（5）和式（2）可得:

2）参考值计算与分析

由图2（b）可知,变压器一次侧补偿电压U̇tr的幅值Utr和相位β表示如下:

式中:UL为负载电压U̇L的幅值；US为电网电压U̇S的幅值。

此时,İcn的幅值Icn与相位δ可表示如下:

式中:ω为角频率。

结合式（6）和式（10）可得电网电流İS的幅值IS和相位μ为:

假定φ为负载功率因数角,则所提变流器的输出有功功率Pin和无功功率Qin可表示如下:

式中:IL为负载电流İL的幅值。

最终,以有源部分输出有功功率最小为目标,结合式（7）、式（8）、式（11）—式（13）,可得有源部分输出电压参考值U̇*C1的控制相位α。此外,为使U̇L的幅值在补偿后保持不变,由式（3）可知U̇*C1的幅值即是负载电压额定幅值U*Lm,从而得到有源部分输出电压参考值。

1.2.2 并联补偿模式

当电网电压正常时,开关S1闭合、开关S2断开,MF-GCC 工作在并联补偿模式。MF-GCC 在并联补偿模式下的拓扑和等效电路如图3（a）和（b）所示,MF-GCC 有源部分在此模式下等效为受控电流源。

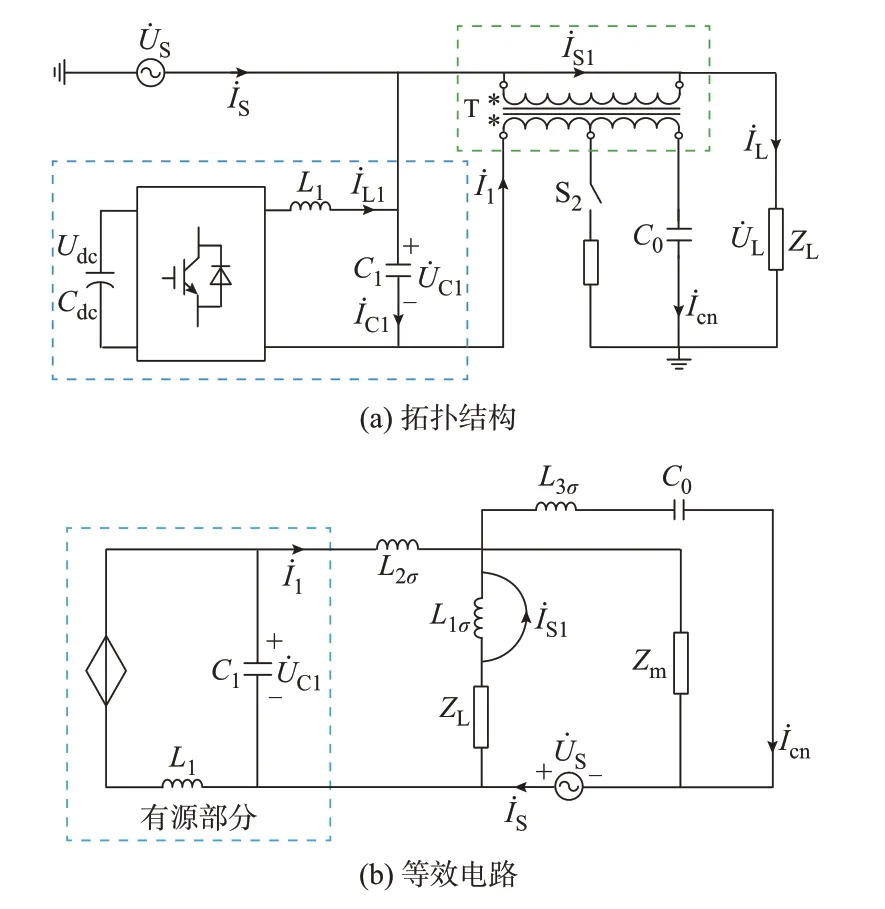
图3 MF-GCC 在并联补偿模式下的电路图Fig.3 Circuit diagram of MF-GCC in shunt compensation mode

并联补偿模式时,控制量为并网电流İ1,通过控制其幅值和相位的变化,实现类似于并联型变换器的无功补偿功能。考虑到并联补偿模式下的工作原理与传统并联型无功补偿装置无较大区别［21］,故不再赘述。

2 MF-GCC 的不同模式柔性切换策略设计

当配电网发生电压波动时,MF-GCC 从并联补偿模式切换至串联补偿模式,待到电网电压恢复后,MF-GCC 又从串联补偿模式切换到并联补偿模式。在模式切换过程中,合理的开关动作时序将会防止装置元部件遭受电压和电流等瞬态冲击,进而保证设备和电网的安全、可靠运行。

2.1 并-串联补偿模式柔性切换原则与逻辑

假设配电网在t0时刻发生跌落/抬升故障,MFGCC 的S1、S2以及变流器中绝缘栅双极型晶体管（IGBT）控制信号按照合理的逻辑顺序动作后,完成并联补偿模式至串联补偿模式的切换。假设不同开关按照t1、t2、t3时刻顺序进行动作,不同开关动作逻辑方案应满足以下原则。

1）不同量值的电流源不能串联

假设t1时刻S1断开,负载电流流过变压器一次侧,故此时流过变压器二、三次侧的电流为负载电流的一半,变压器二、三次侧可等效为一个输出电流受负载电流钳位的电流源。同时,MF-GCC 有源部分仍处于并联模式,也等效为一个输出无功补偿电流i1的电流源。结合S1断开后的等效电路图（详见附录A 图A2）可以看出,变压器二、三次侧等效电流源与MF-GCC 有源部分等效电流源串联。考虑到电路中不同量值的电流源不能串联［22］,故该现象与电路理论相矛盾。因此,S1不能在t1时刻动作,可得几种开关动作逻辑方案,如表1 所示。

表1 并-串联切换逻辑方案Table 1 Logic scheme of parallel-series switching

2）控制信号切换不引起电路振荡

假设t1时刻切换IGBT 控制信号,MF-GCC 有源部分等效于从电流源切换至电压源,如附录A 图A3 所示,由于Zm较大,Zm回路视作开路。开关K 由1 接至2,电路输入发生变化,由于变压器二、三次回路中无阻尼成分,属于欠阻尼状态,电路中相关电气量振荡［23］。因此,不能在t1时刻切换IGBT 控制信号,方案1、4 不可取。

3）MF-GCC 输出电流应满足裕度

在t1时刻S2闭合后,假设t2时刻切换IGBT 控制信号,变压器二、三次回路等效电路图如附录A 图A4 所示,MF-GCC 有源部分输出电流i1表示为:

式中:u和uS分别为MF-GCC 有源部分输出电压参考值和电网电压的时域表示形式。

由于阻尼电阻Rn值较小,导致式（14）中i1较大,甚至超出MF-GCC 有源部分输出电流额定裕度,影响装置的安全运行。因此,方案3 不可取。故最终选择方案2 所列有源器件动作顺序为并联至串联模式的最佳柔性切换逻辑。

2.2 串-并联补偿模式柔性切换原则与逻辑

2.2.1 串-并联补偿模式柔性切换原则

当电网电压在t4时刻恢复正常后,控制S1、S2以及IGBT 控制信号按合理的逻辑顺序依次在t5、t6、t7时刻动作,MF-GCC 从串联补偿模式切换至并联补偿模式。为便于从微分方程模型角度分析切换过程,本小节各电流、电压变量均采用时域形式,即小写字母表示,各变量含义与1.1 节中定义相对应。各开关的动作逻辑需要满足以下原则。

1）避免utr对uL的影响

在t4时刻电网电压恢复正常后,为了避免MFGCC 输出补偿电压utr对uL的影响,保证负载侧正常稳定运行,应首先在t5时刻闭合S1。由此,可得两种开关动作逻辑方案,如表2 所示。

表2 串-并联切换逻辑方案Table 2 Logic scheme of series-parallel switching

2）避免S1闭合产生瞬时电流冲击

对t5时刻S1闭合瞬间电路中冲击电流的发生机理进行分析。附录A 图A5 为t5时刻之前变压器二、三次回路等效电路图。根据KVL,可得t5时刻之前uC0和uC1为:

因Rn数值较小,Rn在变压器三次回路中分压较小,为便于分析,取uR≈0,则式（15）变为:

t5时刻之后变压器二、三次回路的等效电路图如附录A 图A6 所示。变压器一次侧被短接,因此utr1=utr2=0,同理,可得回路中电压关系如下:

根据式（16）和式（17）可知,t5时刻S1闭合后耦合电容电压突变至零,滤波电容电压突变至uS。在S1闭合前后,耦合电容电压与滤波电容电压变化均为utr1（串联模式下的补偿电压）,从而引起电流icn、i1产生较大瞬时冲击,威胁设备与电网可靠运行。

2.2.2 串-并联补偿模式柔性切换逻辑

根据2.2.1 节分析可知,方案5、6 中S1闭合瞬间均会导致滤波/耦合电容电压突变,从而引发滤波/耦合电容支路过电流,对装置的运行产生威胁。因此,在t5时刻S1闭合之前,有必要添加端口电压相位平滑过渡环节来有效避免电压突变产生瞬时电流冲击,具体原理如下。

1）端口电压相位平滑过渡

由2.2.1 节分析可知,S1闭合时,İcn瞬时冲击的产生是由于U̇C1突变为零。根据1.2.1 节串联补偿模式工作原理可知,控制U̇C1的初始相位θ0平滑过渡到0°,即可实现U̇C0平滑过渡至零。滤波电容电压相位θ变化曲线如附录A 图A7（a）所示,t4时刻电网电压恢复正常,t4a、t4b为U̇C1相位平滑过渡时刻,Δt为过渡时间段,t5时刻S1闭合。U̇C1相位θ在Δt内平滑过渡过程为:

U̇C1相位平滑过渡相量图如附录A 图A7（b）所示。图中,U̇′C1为过渡期间滤波电容电压,U̇′tr为过渡期间变压器一次侧电压。通过式（18）得到θ的初始值、终值以及过渡值。由此可将U̇C1逐步旋转到与U̇S重合,U̇tr以及U̇C0也随着U̇C1的旋转逐步过渡到零,此外,U̇C1的旋转过程不影响负载电压。

2）平滑过渡后确定开关动作逻辑

t4a～t4b时段U̇C1相位平滑过渡后,t5时刻S1闭合,t6、t7时段开关动作逻辑未定。S1闭合后变压器二、三次回路等效电路图如附录A 图A8 所示。由于滤波电容平滑过渡环节中U̇C1的终值为U̇S,结合图A8可知,MF-GCC 有源部分输出电流İ1=0。此外,Rn与C0等效被短接,下一步若断开S2,C0两端电压不会发生突变,有效避免冲击电流产生。因此,在t6时刻断开S2,在t7时刻切换IGBT 控制信号。综上,故最终选择方案5 所列有源器件动作顺序为串联至并联模式的最佳柔性切换逻辑。

3 MF-GCC 整体控制策略

在电网电压处在正常/波动状态时,MF-GCC处在并联/串联补偿模式。而当电网发生电压跌落时,MF-GCC 从并联补偿模式切换至串联补偿模式,待到电网电压恢复后,MF-GCC 又从串联补偿模式切换到并联补偿模式。MF-GCC 不同模式的控制策略如图4 所示,其中,PLL 表示锁相环,PI 表示比例-积分控制器,PWM 表示脉宽调制。首先,对电网电压幅值进行检测,得到dS。然后,根据dS对电网的运行状态进行判断:当0.91.1 时,判定电网电压发生波动,开关S2闭合、开关S1断开,切换IGBT 控制信号,MFGCC 工作于串联补偿模式。

图4 MF-GCC 不同模式的控制策略Fig.4 Control strategy of MF-GCC in different modes

1）变流器在并联补偿模式下的控制策略

2）变流器在串联补偿模式下的控制策略

根据串联补偿模式下的工作原理,首先,由U̇S检测模块确定dS；其次,由式（7）、式（8）、式（11）—式（13）得到U̇L的控制相位α,α与负载电压幅值U相结合即可得到负载电压参考值,补偿电压参考值就是和U̇S的差；最终,结合式（19）可得,再通过内外环跟踪与正弦脉宽调制（SPWM）输出变流器IGBT 的控制信号。

3）多模式柔性切换策略

图5 是电网电压波动（以跌落为例）从发生到恢复正常过程中,各开关以及控制信号的动作时序,1 表示开关闭合,0 表示开关断开。t0时刻电网电压跌落,经短暂延时后,t1时刻S2闭合,t2时刻S1断开,t3时刻变流器的控制信号切换至串联补偿模式对应的控制信号。至此,MF-GCC 进入串联补偿模式。当t4时刻电网电压恢复后,经过短暂延时,t4a～t4b时段控制滤波电容电压相位平滑过渡至零,t5时刻S1闭合,t6时刻S2断开。t7时刻变流器的控制信号切换至并联补偿模式对应的控制信号,MF-GCC 恢复至并联补偿模式。

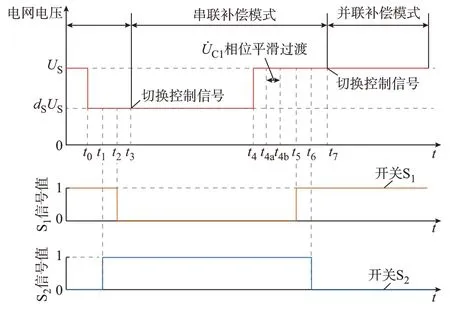
图5 开关及控制信号的动作时序图Fig.5 Action sequence diagram of switch and control signals

4 仿真验证

根据图1,本文在MATLAB/Simulink 中搭建仿真模型,验证本文所提多模式切换方案的有效性,具体仿真参数如表3 所示。

表3 仿真参数Table 3 Simulation parameters

4.1 并-串联补偿模式切换仿真分析

电网电压从正常转变至跌落工况下的仿真波形如附录A 图A9 和图A10 所示。图A9（a）至（d）为未采用并-串联模式柔性切换下的波形图,切换逻辑为:S1断开→IGBT 控制信号切换→S2闭合,图A10（a）至（d）为采用所提柔性切换策略下的波形图。S1与S2考虑采用电力电子器件,其选型和耐受电压、电流应力有关。对于开关S1而言,流过S1电流为负载电流和变压器一次侧电流之和,S1耐压是系统电压。对于开关S2而言,流过S2电流为有源部分输出电流和耦合电容支路电流之和,耐压水平与S2支路电流及该支路上的电阻Rn大小有关。

在0～0.1 s 期间,电网正常运行（dS=1）,MFGCC 处在并联补偿模式,如图A9（b）和A10（b）所示,U̇S与İS在无功补偿后相位相同,网侧实现单位功率因数运行。在0.1～0.2 s,电网电压处在跌落状态（dS=0.8）,结合图A9（a）和图A10（a）可知,在电压波动时,所提变流器可有效输出补偿电压,实现负载侧电压恒定。

此外,由附录A 图A9（c）和（d）可以明显看出,未采用并-串模式柔性切换下,t=0.102 s 开关S1断开,t=0.103 s 时IGBT 控制信号切换,t=0.104 s 开关S2闭合。在各开关动作的瞬间,İnn、İS1、İ1、İS均产生较大的瞬时冲击,负载侧在切换过程中也出现较大电压冲击。由图A10（c）可以明显看出,在t=0.102 s 之前İnn为零,t=0.102 s 开关S2闭合,S2所在支路导通。t=0.103 s 时开关S1断开,İS1变为零。t=0.104 s 时IGBT 控制信号切换,MF-GCC 有源部分的输出电压和电流相应改变,如图A10（d）所示。此外,本文充分考虑了检测延时对运行切换造成的影响,故在仿真与实验中,在并-串联补偿模式切换动作初期,均加入1 ms 延时模拟检测环节带来的影响。各开关动作的逻辑顺序与2.1 节分析一致,在整个并-串联补偿模式切换过程中,各电气量均未产生较大突变,MF-GCC 和电网的运行可靠性得到了保证。

4.2 串-并联补偿模式切换仿真分析

电网电压从跌落工况转变至正常工况下的仿真波形如附录A 图A11 和图A12 所示。图A11（a）至（d）为未采用串-并联补偿模式柔性切换下的波形图,图A12（a）至（d）为采用2.2.2 节所提切换方案下的波形图。0.2～0.3 s 期间,所提变流器工作于串联补偿模式,实现负载侧电压恒定,如图A11（a）和图A12（a）所示。0.3～0.4 s 期间电网正常运行（dS=1）,MF-GCC 处在并联补偿模式,如图A11（b）和图A12（b）所示。

未采用串-并联补偿模式柔性切换下,在t=0.307 s 开关S1闭合瞬间İS、İS1、U̇C1、İ1均产生较大的瞬时冲击,如图A11（c）和（d）所示,威胁设备和电网的正常运行。采用所提切换方案后,MF-GCC 在t=0.302～0.304 s 期间实现滤波电容电压相位过渡,再按照所分析的逻辑时序完成各开关动作,如图A12（c）和（d）所示。仿真结果表明,MF-GCC 可以平滑地从串联补偿模式切换至并联补偿模式,验证了理论分析的正确性和可行性。

5 实验验证

为了进一步验证本文所提MF-GCC 多模式切换方案的有效性,本文基于第4 章的仿真模型搭建实验平台,实验参数与表3 一致。电网电压抬升和跌落时MF-GCC 从并联模式切换至串联模式的实验波形如图6 所示。

图6 MF-GCC 并-串联模式切换的实验波形Fig.6 Experimental waveforms of MF-GCC in parallel-series mode switching

电网在t0时刻之前保持正常运行状态（dS=1）,MF-GCC 处在并联补偿模式。t0时刻电网电压抬升（dS=1.2）/跌落（dS=0.5）,经过1 ms 延时,t1时刻闭合S2,t2时刻断开S1,t3时刻切换IGBT 控制信号,MF-GCC 此后进入串联补偿模式。从图6 中可以看出,各电气量在并-串联补偿模式切换过程中均无冲击。

电网电压恢复正常时,MF-GCC 从串联模式切换至并联模式的实验波形如附录A 图A13 和图A14所示。t4时刻之后电网电压恢复正常（dS=1）。从图A13 和图A14 中可以看出,各电气量在串-并联补偿模式切换过程中只存在较小冲击,MF-GCC 可以平滑地从串联补偿模式切换至并联补偿模式,验证了所提多模式柔性切换策略的正确性和可行性。