基于深度强化学习区间多目标优化的智能建筑低碳优化调度

侯 慧，何梓姻，陈 跃，2，侯婷婷，唐金锐，吴细秀

（1.武汉理工大学自动化学院,湖北省武汉市 430070；2.国网湖北省电力有限公司十堰供电公司,湖北省十堰市 442000；3.国网湖北省电力有限公司经济技术研究院,湖北省武汉市 430077；4.武汉理工大学深圳研究院,广东省深圳市 518000）

0 引言

据清华大学建筑节能研究中心发布的《中国建筑节能年度发展研究报告2022（公共建筑专题）》,2020 年建筑运行总能耗占全国能耗总量的21%,预计到2050 年,建筑节能潜力达74%,可减少碳排放约50%［1］。随着多种形式能源及分布式发电资源的渗透,传统用能建筑正转变为以建筑为主体的多能源系统［2］。因此,如何开展建筑优化调度与能量管理,已成为实现建筑经济运行、促进建筑减排的关键问题。

近年对于智能建筑已有许多研究。针对建筑热特性,文献［3］通过建筑热力学简化一阶热模型,评估了建筑运行条件对建筑供能灵活性的影响。文献［4］将考虑建筑围护结构的对流换热、门窗渗透、冷风侵入和内热源散热等因素的热平衡模型引入调度问题,以提升室内温度计算的精确性。具体到建筑中暖通系统,文献［5-6］提出了对商业建筑中暖通系统的监督控制,为电网提供频率调节服务。其中,文献［6］通过与储能技术比较,表明建筑温控负荷的调控更具经济效益。上述研究基于建筑热特性展开,但未涉及需求响应调控。文献［7］构建了基于阶梯型补贴的需求响应机制下含精细化建筑虚拟储能的综合能源站经济调度模型,综合考虑多种热量扰动因素,统筹协调能源站与用户侧的资源。文献［8-9］通过电热能源耦合替代进行协同控制,基于电价预测模型预测运行。然而,上述研究未在计及新能源出力及负荷需求等不确定性因素的同时,统筹考虑居住者体验、天气及建筑结构特性等。

针对需求侧资源,尤其是能耗占比大的智能建筑系统的减排潜力亟待开发。同时,随着碳交易机制的引入,智能建筑的分布式发电等因素的强随机性、波动性等特点也更加显著,这对调度策略及不确定求解方法也提出更高要求。现有不确定性研究的主要方法包括备用容量调度［10-11］、随机规划［12-14］、场景分析［15-17］、鲁棒优化［18-19］及区间优化［20］等。文献［10］提出了一种综合考虑发电机故障等约束下储能作为备用容量的调度方法。文献［11］通过储能等备用容量进行微网两阶段不确定性调度。文献［12］计及光伏及能源价格的不确定性,提出了一种建筑能源管理的随机规划模型。文献［13-14］构建了两阶段随机规划模型,将新能源出力不确定性整合到优化中。文献［15-16］基于场景分析方法构建了微网能源管理模型。文献［17］采用场景生成及场景削减的方法处理可再生能源的不确定性。文献［18］建立两阶段鲁棒优化模型,考虑可再生能源与负荷不确定的同时,兼顾系统调度成本及运行可靠性。文献［19］基于鲁棒优化建立了高比例可再生能源渗透的配电网储能规划模型,并通过蒙特卡洛抽样验证了可行性。文献［20］通过区间数将不确定性转换为区间表达式,建立了一种针对蓄热建筑的多时间尺度区间优化调度模型。整体而言,备用容量调度会增加系统的容量配置成本,随机规划及场景分析方法则会影响结果准确性。鲁棒优化在处理不确定问题方面具有一定优势,但基于最坏情景来优化系统运行势必会使优化结果偏于保守,难以满足运行经济性。区间优化通过将不确定性因素转化为区间数,并求解得到相关不确定变量的决策区间,可有效解决上述在实际应用中大量不确定信息困难问题,但区间过大可能影响结果精确度及算法收敛性等［21］。

深度强化学习将感知、学习及决策等整合到同一个框架内,不需要通过精确的数学公式刻画物理模型信息。因此,基于深度强化学习的方法可以捕捉到难以精确建模系统的动态特性,在一些高维复杂任务中的表现优于传统基于模型的优化算法,能更好地处理优化过程中的动态问题。深度强化学习单独作为动态优化算法或结合机器学习模型在微网实时调度［22-23］及负荷预测［24］等领域已取得较好效果,但对于提高优化算法性能的参数优化方面还鲜有研究。

基于以上分析,本文提出多重不确定性影响下基于深度强化学习的区间多目标优化智能建筑调度方法。在源荷不确定性基础上,考虑建筑热弹性、设备参数、响应程度、智能建筑围护参数、环境温度等多重不确定性因素,采用区间数等方法进行建模；以运行成本最低及用户舒适度最优为目标,提出基于深度强化学习的区间多目标粒子群算法对其求解,通过深度强化学习指导区间多目标优化,提升寻优效率及算法收敛性,以实现系统最优运行。最后,通过算例仿真验证本文所提方法的有效性。

1 不确定性建筑能量管理系统模型

经典的智能建筑系统如图1 所示。能源供给侧由上级电网、上级气网等组成,同时,建筑具有分布式电源单元协同供给。建筑内机组设备根据用户需求安排生产计划,在满足用户基本需求的同时,协同、转换用能形式,提高经济性。

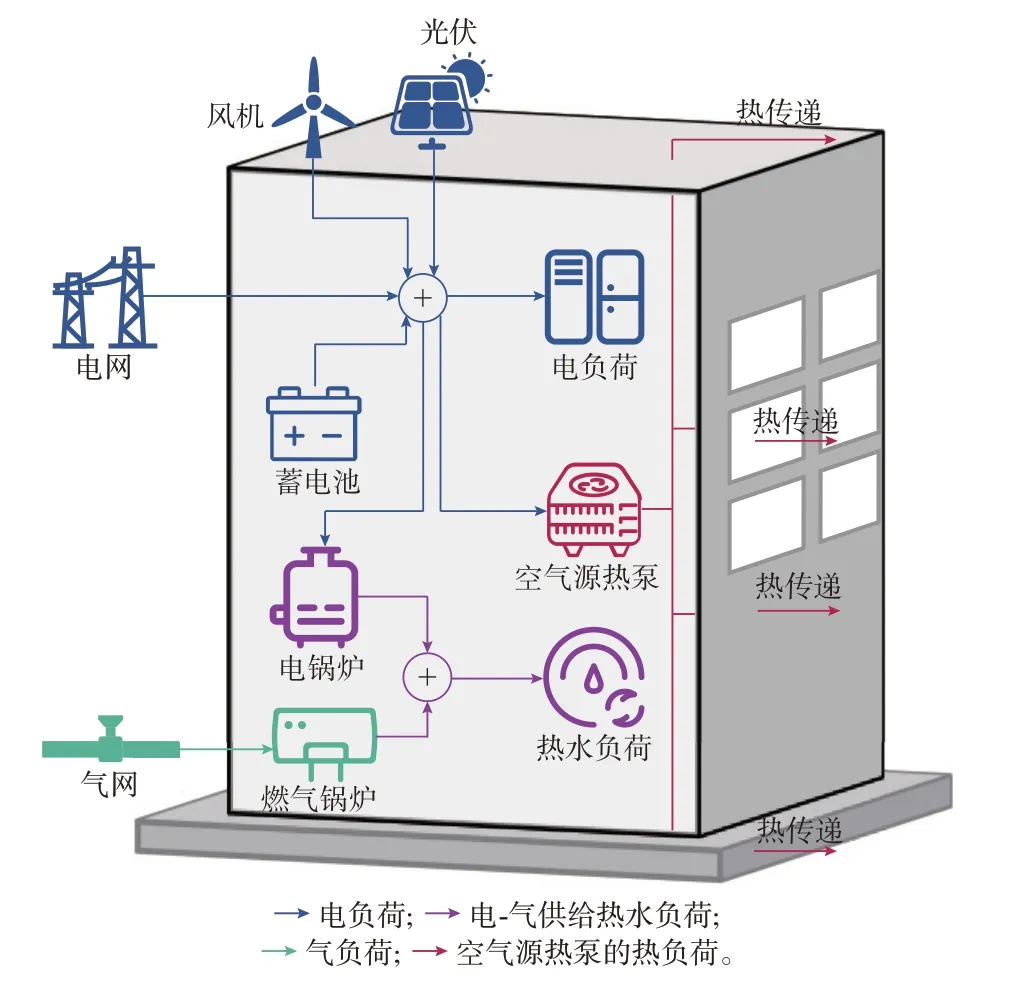
图1 智能建筑系统结构Fig.1 Structure of smart building system

建筑内部机组主要包含电空调、电热水器与燃气锅炉（gas boiler,GB）等设备,以满足建筑内部供电、供暖及热水等各类需求。本文假设上述建筑供能设备可由建筑物能源管理系统统一进行智能控制。

1.1 电气设备不确定性模型

本文将建筑内部电气设备因温度、湿度、负载率等外界因素影响下的变工况运行特性看作不确定性因素,对机组转换效率不确定性区间建模如下。

1.1.1 电锅炉

系统中电锅炉（electric boiler,EB）可满足用户部分热负荷需求,考虑转换效率不确定性,其模型如式（1）所示。

式中:上标“±”表示区间变量；QEB,t为t时刻EB 输出热功率；PEB,t为t时刻EB 消耗的电功率；ηEB为EB制热效率。

1.1.2 GB

GB 通过燃烧天然气为建筑系统用户集中供热,满足用户主要热需求,其模型如式（2）所示。

式 中:QGB,t为t时 刻GB 输 出 热 功 率；VGB,t为t时 刻GB 耗气量；ηGB为GB 产热效率；Hg为天然气热值。

1.1.3 空气源热泵

空气源热泵（air-source heat-pump,AH）也是系统的电-热能源耦合装置之一,其数学模型如式（3）所示,环境温度对AH 的影响模型如式（4）所示［4］。

式中:QAH,t为t时刻AH 制热功率；PAH,t为t时刻AH消耗的电功率；ηAH,t为t时刻AH 制热能效比；Δt为时间间隔；αi为幂级数i下制热能效比拟合系数；Tout,t为t时刻室外环境温度。

1.1.4 蓄电池

蓄电池（battery energy storage,BES）主要用于系统新能源消纳、新能源出力缓解、负荷波动平抑等。其充放电模型如式（5）所示。

式 中:SBES,t为BES 在t时 刻 的 荷 电 状 态；PBES,t为BES 在t时刻的出力,值大于0 为放电,值小于0 为充 电；EBES为BES 容 量；σBES为BES 自 损 耗 系 数；ηBES,c和ηBES,d分别为BES 充、放电系数。

1.2 建筑热弹性模型

现有研究在衡量建筑蓄热特性时通常采用简单的电阻电容等值电路模型［8］。本节在此基础上,采用基于围护结构的热传递模型,如式（6）所示。

式中:Tin,t为t时刻建筑系统室内温度；ΔTt为Δt时段内建筑系统室内温度变化,如式（7）所示。

式中:S为建筑系统占地面积；H为建筑室内高度；ρair为 空 气 密 度；Cair为 空 气 比 热 容；Qhd,t为t时 刻 围护结构的耗热量,如式（8）所示。

式中:Oarc为建筑围护结构集合；α为由围护结构空间位置导致的温差修正系数；kj为第j类围护结构传热系数；Sj为第j类围护结构面积。

1.3 源荷不确定性模型

影响新能源出力以及负荷需求变化的因素众多,通常难以获得完备的数据。文献［25］表明风电/光伏/负荷具有混沌特性,采用相空间重构技术对历史数据进行处理,可不考虑除历史数据以外的影响因素。本节采用相空间重构及机器学习结合的方式,将相空间重构后的高维相空间作为机器学习模型的训练输入数据进行预测。

基于数据驱动的预测算法及非参数核密度估计法构建源荷不确定性模型［25-26］,无须进行先验假设,具有更强的适应性,包含点预测与区间预测两部分。点预测仅能预测单点期望值,难以反映不确定性,而区间预测输出的是可能变化的区间［25］。因此,可采用区间预测对新能源出力与负荷进一步预测。基于核密度估计法［26］得到预测误差的概率密度函数及概率分布函数F(ζ),通过F(ζ)反函数计算得到给定置信水平下的预测区间。以系统用户电负荷为例,t时刻的点预测值为PEL,pre,t,预测误差为ξEL,则在置信水平为1-β下的预测区间可表示为:

式 中:PEL,t为t时 刻 系 统 电 负 荷 需 求；EL,t和EL.t分别为t时刻系统电负荷需求上、下界。

2 计及碳交易的区间多目标优化调度

智能建筑的供能设备、新能源出力等具有强随机性与波动性,现有研究缺乏对智能建筑系统中多重不确定性的统筹考虑。同时,在经济调度过程中大多仅考虑调度成本,较少研究计及系统用户舒适度方面的影响,存在一定的片面性。因此,本文计及系统用户对于运行经济性及人体舒适度的要求,综合考虑碳排放等因素的影响,计及多重不确定性及多元调度目标,构建区间多目标优化调度模型。

2.1 碳排放与碳交易机制

2.1.1 系统碳排放计量

本文所构造的建筑系统模型包含电、热、气等多种形式能源,且各种能源相互耦合。为清晰界定不同能源引起的碳排放,本文采用生命周期评价（life cycle assessment,LCA）法［27］对不同能源链迁移转化过程中的碳排放进行计量,充分考虑每条能源链从生产源头到负荷需求侧的碳轨迹,精确判断建筑系统碳排放总量。

式中:E为系统碳排放总量；eq为系统设备q相应能源种类能源链碳排放量系数；ec,q、et,q、eu,q分别为系统设备q相应能源种类生产环节、存储运输环节及使用环节的碳排放量系数；Ω为系统能源供应存储环节设备集合；Pq,t为t时刻设备q的有功功率；T为系统调度周期。

2.1.2 碳交易机制

碳交易最初是由联合国为应对气候变化创建的一种贸易体系。碳交易机制通过建立合法碳排放权并允许对其进行买卖,实现碳排放量控制［27］。本文根据碳权分配基线法进行系统碳排放成本的归算［28］,系统碳交易成本如式（13）所示。

式中:c(·)为碳交易成本函数；E*为系统碳排放权配额；ξ为碳价。

2.2 目标函数

系统优化目标为综合经济成本最低与人体热舒适度最优。

2.2.1 综合经济成本

经济调度过程中综合成本主要包含系统购能成本、机组运维成本及系统碳交易成本等。

式中:F1为综合经济成本子函数；fe、fma、fc分别为系统购能成本、机组运维成本、系统碳交易成本；Pgrid,t为t时刻电网功率；peb,t和pes,t分别为系统向电网购电及售电价格；pg为系统购气气价；c、c、c、c分别为调控周期内EB、GB、AH、BES 的单位运维成本。

2.2.2 人体热舒适度

为了更全面表征用户舒适度,本文引入根据国际标准ISO 7730 制定的人体热舒适度预测平均指标（predicted mean vote,PMV）［29］来量化用户的冷热舒适度。忽略室内风速、湿度等影响,PMV 计算公式可简化为式（18）。

式中:IPMV,t为t时刻建筑系统内用户PMV 值；Tsk为舒适温度；M和Icl分别为人体代谢率和服装热阻。

PMV 是一个综合性指标,将人体舒适度量化在[-3,3]内。PMV 与用户舒适度关系如附录A 图A1 所示,PMV 值为负表示人体产生冷的感觉,值为正表示人体产生热的感觉,其绝对值越大,表示感觉越强烈,-0.5～0.5 为合理的人体舒适环境。人体热舒适度子函数可表示为:

式中:F2为人体热舒适度子函数,为区间函数,表征调控过程中建筑系统热环境脱离人体生理舒适环境整体程度；‖ · ‖2表示 二范数。

2.3 运行约束

针对构建的调度模型需满足以下约束条件。

2.3.1 功率平衡约束

式中:PPV,t和PWT,t分别为系统风、光功率预测值；PTL,t为系统热负荷需求预测值。

2.3.2 设备功率约束

式 中:QEB,max、QGB,max、QAH,max、PBES,max分 别 为EB、GB、AH、BES 的最大输出功率。

2.3.3 储能容量约束

除储能设备输出功率约束外,还应满足荷电状态约束,如式（26）所示。同时,考虑到储能调度周期的连续性［30］,调度周期始末系统储能状态应保持一致,如式（27）所示。

式中:SBES,min和SBES,max分别为荷电状态最小值和最大值；SS,0和SS,T分别为调度周期T始、末系统储能状态。

3 深度强化学习区间多目标优化算法

本章针对上述考虑碳交易的多重不确定性模型调度求解问题,构建了基于深度强化学习的区间多目标优化算法。区间多目标优化问题是实际应用中普遍存在且复杂的优化问题。由于问题的目标函数取值不再是精确数值,同时,区间目标使非支配解数量快速增长,致使传统区间多目标优化算法如区间多目标粒子群优化（interval multi-objective particle swarm optimization,IMOPSO）算法等,面临巨大选择压力,且存在算法迭代寻优效率下降、区间收敛困难等问题。

深度强化学习利用神经网络拟合状态动作价值函数,并根据状态价值函数指导对象运动,更好地处理优化过程中的动态问题。通过离线历史数据进行模型训练,能够应用于在线的策略生成,极大缩短策略生成时间,将已有模型应用在其他类似场景时,可以进行模型自主进化。基于此,本文利用深度强化学习与IMOPSO 算法交互,从而学习建筑模型状态、动作、奖励间的隐式关系,进而指导区间种群运动,实现Pareto 前沿的快速逼近与区间收敛。最后,利用模糊隶属度函数从Pareto 解集中权衡筛选出最终调度方案。本文模型求解框架如图2 所示,具体模型与算法耦合关系如附录A 图A2 所示。

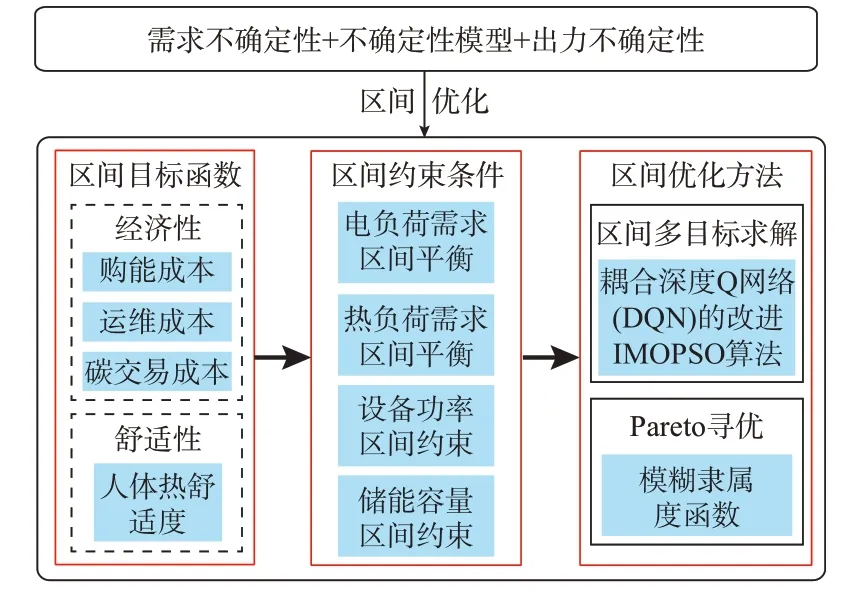
图2 模型求解框架Fig.2 Model solving framework

3.1 深度强化学习模型

强化学习的本质是当前对象（Agent）与环境的交互。交互过程中涉及动作-状态转移与状态价值函数奖惩,实现满足目标期望的迭代学习优化,使得Agent 最终获得最多的累计奖励。

3.1.1 状态与动作

在IMOPSO 迭代求解过程中,强化学习模型中智能体即为概念实体IMOPSO 算法。

IMOPSO 算 法 具 体 为 含Dimen维 变 量、Mpop,size个粒子的区间种群优化Nobj维目标。设粒子m的位置为,速度为,个体历史最优位置为,群体最优位置为,则状态、动作如式（28）和式（29）所示。

式中:S为智能体状态；A为智能体决策动作；ω为初始网络权重；c1和c2为权重ω下的两种动作。

3.1.2 奖励函数

本文将奖励函数设定为种群IMOPSO 粒子适应度及其区间长度。

式中:R(·)为奖励函数；βz为第z类系数；z∈{d,l}表示包含适应度和区间长度两类要素；fz和fz,max分别为第z类当前奖励及最大程度优化所对应的奖励；fm和fl分别为适应度和区间长度奖励值；F±n为第n个子目标区间函数,共计Nobj个目标；δn为目标n的 权 重；d(·) 为 区 间 中 值 函 数；l(·) 为 区 间 长 度函数。

3.1.3 动作决策

动作决策过程为Agent 由当前状态根据决策网络做出动作决策,同时引入ε-greedy 机制:

式中:At为t时刻智能体决策动作；“random”表示有ε的概 率取随机动作；p为随机数；St为t时刻智能体所处状态；Q(·)为智能体决策的网络,有1-ε的概率取网络最大输出对应动作值,网络可由贝尔曼方程定义。

式中:Q(St+1,A)为t+1 时刻在状态St+1下可能得到的网络输出；β′和γ分别为网络更新学习因子和折扣因子。

3.2 耦合DQN 的改进IMOPSO 算法

为解决区间多目标优化问题,提出一种耦合DQN 的改进IMOPSO 算法,优化功能实现具体分为“离线训练”和“在线指导”两部分,如附录A 图A3所示。

3.2.1 离线训练

在“离线训练”过程中,IMOPSO 将状态传入智能体得到决策动作,并进行状态奖励评价以及网络训练优化。网络训练过程为:基于经验回放机制,智能体将IMOPSO 迭代一次得到的四元数组[St,At,Rt,St+1]储存在记忆池中,记忆池通过不断的存储、溢出,保持实时更新,其中,Rt为t时刻奖励函数。在网络参数更新中,通过式（33）构造标签,并引入目标网络用于输出最大目标值maxQ(St+1,A)。

3.2.2 在线指导

在“在线指导”部分,首先导入训练完成的网络,其中存放了提升算法综合性能最大的动作策略。然后初始化种群,与各网络一一对应。最后,反复调用网络,在线指导个体运动,完成算法迭代寻优直至收敛。模型中状态为种群位置速度等,动作对应参数选择,测试环境为IMOPSO 算法整体规划过程,训练的参数策略对于不同优化场景具有通用性。

4 算例分析

4.1 算例参数设置

本文风机/光伏/负荷数据来源为美国PJM 电网的数据管理工具Data Miner 2 网站［31］。对系统采取日前调度,时间间隔为1 h。设备运行参数如表1所示［32］,建筑系统参数如表2 所示［32］,电/气交易价格见附录A 图A4。

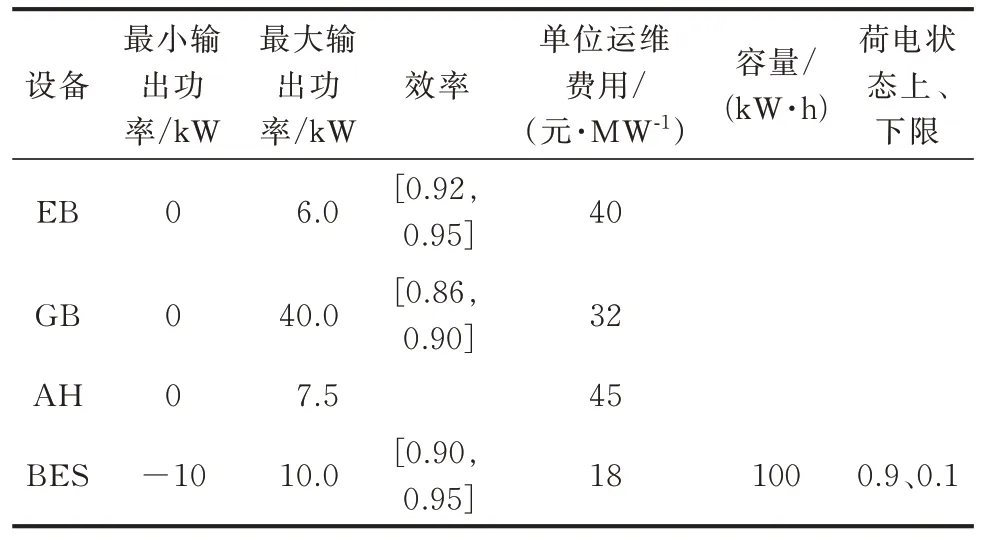
表1 设备运行参数Table 1 Operation parameters of devices

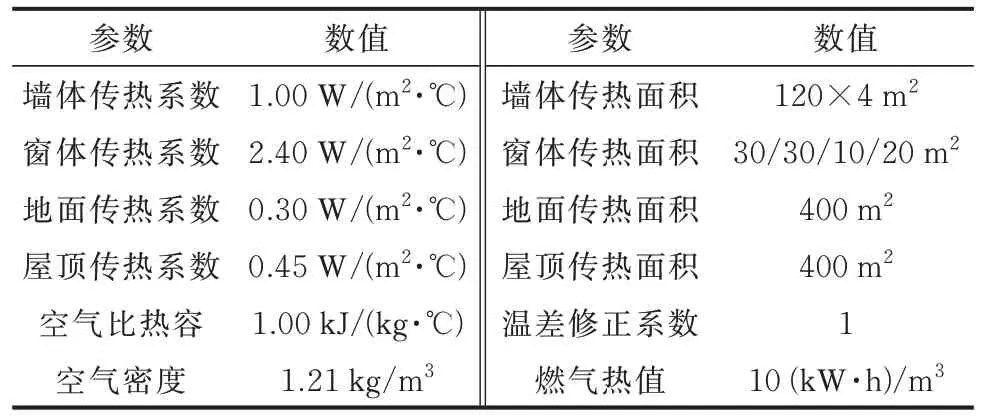
表2 建筑系统建筑参数Table 2 Building parameters of building systems

本文设定经验池容量为500,回放单元样本数为20,探索率为0.1,折扣因子为0.9,学习因子为0.1,目标网络更新步长为10,训练步数为5 000,测试步数为500。网络学习率取0.001。状态空间维数作为神经网络输入,包括粒子个体位置144 维（含EB 出 力 区 间 值48 维、GB 出 力 区 间 值48 维、AH 出力区间值48 维,BES 出力由等式约束确定）、个体速度144 维、个体历史最优144 维、种群历史最优144维,合计576 维。状态空间为30 维,作为网络输出。隐藏层神经元数量分别为1 000、1 000、200。

本文采用超量（hypervolume）指标和不精确度（imprecision）指标衡量算法性能［33］,定义如下。

给定一组预先设置分布在目标空间的参考点r与一组由算法得到的Pareto 近似解集P,满足r被P中所有解支配。超量指标H(P)衡量的是以r为边界、被P支配目标空间的体积大小,可表示为:

式中:v±(p,r)表示参考点r与解集P中单个解p构成的超体积区间。本节将超量的中点用作性能指标,H值越大,表示P越近似于Pareto。

不精确度指标I(P)可以测量所获得解集的不确定性,解集P 的不精确度被定义为:

式中:F(p)为单个解p的不精确度区间函数,解集P的不精确度越小,不确定性性能越好。

4.2 算法仿真试验

4.2.1 区间预测

采用互信息法对历史用户负荷数据及光伏功率数据求取延迟时间,采用伪近邻法求取嵌入维数［34］,所得用户负荷数据的延迟时间和嵌入维数分别为4 和3,光伏功率数据的延迟时间和嵌入维数分别为9 和6。根据延迟时间和嵌入维数分别对各微网用户负荷及光伏功率进行相空间重构。

在选择预测方法时,本文对比多种预测方法及其学习算法［35-40］,采用多种指标评价预测精度［41］,比较结果如表3 所示。其中,极限学习机（extreme learning machine,ELM）预测精度最高,因此,采用ELM 对用户负荷及光伏功率进行预测。

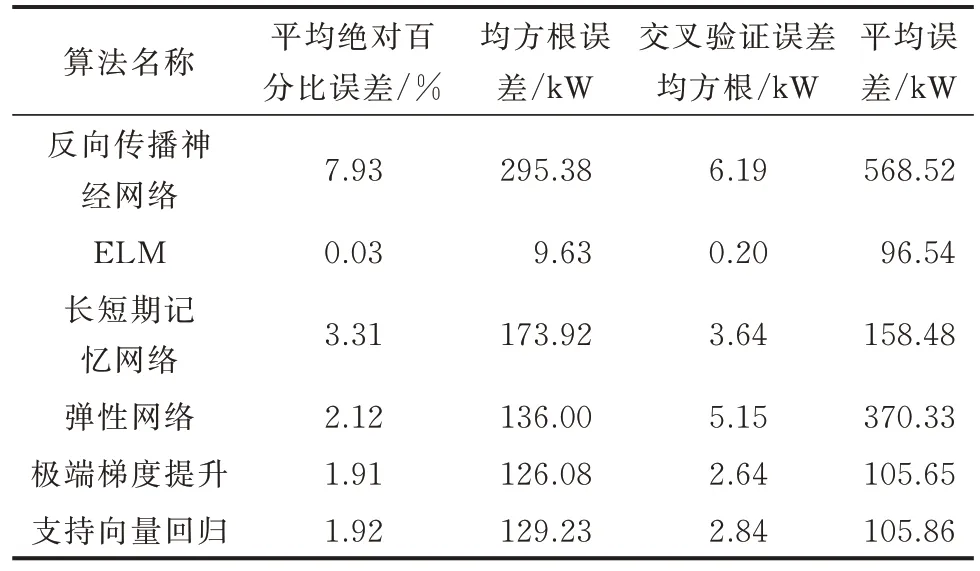
表3 不同机器学习算法的负荷预测结果对比Table 3 Comparison of load forecasting results with different machine learning algorithms

整合点预测结果,在95%置信度水平下对系统的风电/光伏/负荷进行区间预测,结果如图3 所示。图 中:和分 别为t时刻系统用户热负荷、光伏、风机功率的上界和下界；和分别为t时刻室外温度上、下界。

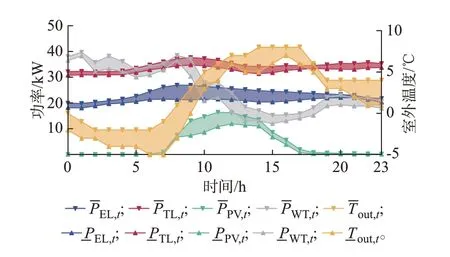
图3 95%置信度水平下区间预测结果Fig.3 Interval forecasting results at 95%confidence level

4.2.2 训练过程

为体现训练过程中粒子运动后的适应度值,网络输出见附录A 图A5。可以看出,在前500 次训练中,由于处于记忆池填充阶段,网络输出稳定在较低值。随后,通过记忆回放机制训练更新网络,网络输出开始提升并伴随振荡。因深度强化学习存在随机探索过程,因此,图A5 中网络输出曲线存在随机波动。整体上,所提算法模型的决策能力呈稳步上升趋势并逐渐趋于稳定。

4.2.3 测试结果

选取种群规模为20,最大迭代次数为500,得到Pareto 前沿见附录A 图A6。Pareto 中非支配适应度解为归一化双区间表现形式,即图A6 中方框区域为区间范围,点表示区间中点。由图A6 可知,综合经济成本与人体热舒适度之间存在矛盾性,即若调度安排更偏重经济成本,则会根据电网电价以及各分布式能源供电成本选择更为廉价的供电方式,可能会造成AH 等灵活性设备出力不足,出现环境舒适性降低的情况。相反地,若偏重舒适性,为改善系统人体热舒适度情况,需要系统相关设备提供更多的功率支撑,此时经济成本灵活性相对不足,不可避免地会增加成本支出。在调控过程中,需要权衡各方因素选择最佳的调度方案。

本文选取Pareto 最优解集中的2 个典型最优解（即经济性方案和舒适性方案）进行对比,调度结果如附录A 图A7 和图A8 所示。从图A7（a）可以看出,经济性方案通过“低充高放”的策略实现电能在不同电价区间转移,从而实现获利,例如,10:00—15:00 时段处于峰时电价,储能放电,向电网售电获利；而00:00—07:00 时段处于谷时电价,储能大幅充电,且此时风电富足,向电网售电。从经济性方案整体电平衡状态出发,可以看到电负荷相对平稳,但AH 调度不频繁。图A7（b）和（c）中,EB 与GB 功率并未跟随热舒适度情况。对于图A7（c）,本文设定灰线范围内为用户舒适度最佳,此时PMV 为-1～1,而经济性方案中,用户热舒适度相对较低,整体在满足建筑系统用户负荷需求的同时更注重经济性。

附录A 图A8 中,舒适性方案显示室内温度基本维持在18～28 ℃范围内,用户舒适度最佳。从 图A8（b）和（c）可以看出,针对热舒适度,AH 调度较经济性方案更频繁,并且在负荷高峰时,功率可调节裕度更少,运行经济成本较高。

对比两种调度方案,若决策者优先考虑经济性因素,经济成本最低可达［407.67,475.39］元,但用户舒适度较差,为［79.54,166.45］。反之,若以用户舒适度为重点,优化目标可达到［62.12,76.01］,将显著增加系统的经济成本,为［833.61,908.49］元。系统调度时应综合权衡以确定规划方案。

4.3 算法有效性分析

为验证本文所提算法的有效性,将本文所提算法与传统IMOPSO 算法对比,IMOPSO 参数采用惯性权重,即分别从个体运动以及种群非劣解的变化过程两方面分析。

4.3.1 个体收敛情况

随机选取某测试中10 个个体,分别比较两种算法个体前两维变量及个体适应度迭代第0、5、10、20 次时的情况。

附录A 图A9 为两种算法个体区间长度分析,其中,不同颜色代表不同个体。比较图A9（a）和（b）可以看到,在迭代过程中,图A9（a）中的个体变量区间长度能够有效迅速收敛,在20 次迭代过后收敛效果明显优于图A9（b）中的个体变量。

附录A 图A10 为两种算法个体运动区间方向分析。耦合DQN 的改进IMOPSO 算法个体适应度值在运动方向上更加明确,个体适应度区间值能够快速聚集于历史最优位置。在20 次迭代时,耦合DQN 的改进IMOPSO 算法收敛效果明显优于传统IMOPSO 算法。同时,区间长度迅速收敛,个体适应度的不确定性大大降低。这直观证明了耦合DQN 的改进IMOPSO 算法奖励函数部分的有效性。因此,耦合DQN 的改进IMOPSO 算法能有效引导个体适应度区间快速收敛。

4.3.2 Pareto 收敛情况

Pareto 前沿的运动收敛过程见附录A 图A11。基于个体运动情况,在Pareto 上呈现为累计效应,即在网络指导下,图A11（a）中种群快速聚集于非支配区域,相较于图A11（b）,区间长度较小,非劣解分散程度更高,前沿更靠前。

综上,耦合DQN 的改进IMOPSO 算法有较强的求解能力,结果的收敛性能和分布性能比传统IMOPSO 算法相对较强,体现了该算法的有效性。

4.4 算法必要性分析

不同参数会对系统调度结果产生一定影响,为精确量化对比最终结果,对本文所提算法与传统IMOPSO 算法进行100 次测试,获得的Pareto 集见附录A 图A12,具体指标见表4。

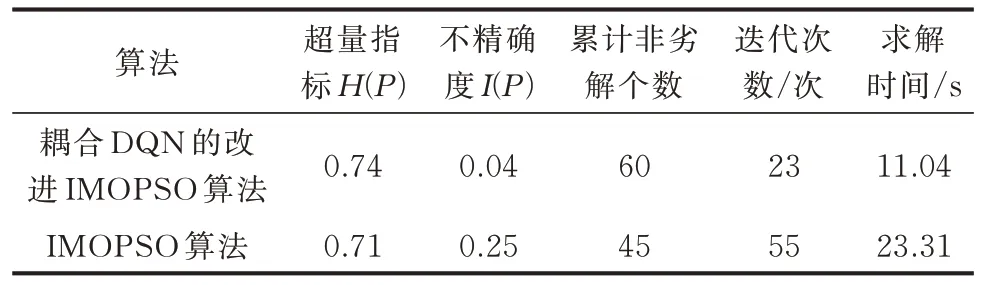
表4 算法对比Table 4 Comparison of algorithms

从附录A 图A12 可以看出,通过耦合DQN 的改进IMOPSO 算法获得的Pareto 最优解集中点和区间比传统IMOPSO 算法所得结果分布更加靠近坐标原点,同时分布更加均匀,区间长度更小,表明结果不确定性更低。表4 显示了这两种算法结果的性能指标平均值,其中,求解时间是载入训练好的深度网络算法求解区间优化问题的时间。可以看出,本文所提算法的超量和不精确度性能指标均优于传统IMOPSO 算法,且求解速度更优。实际调度中,为更好地分析实时调度情况,在确保有效性的前提下缩短求解时间同样非常必要。

4.5 模型效益及系统调度分析

不同参数会对系统调度结果产生一定影响,本节分别从碳交易价格及系统负荷区间置信度等方面分析了模型效益及系统调度情况。

4.5.1 碳交易价格影响分析

对于本模型,改变碳交易价格得到系统各项成本与碳排放量的变化曲线见附录A 图A13。随着碳交易价格的提高,系统碳交易成本整体呈先上升后下降趋势。因为当碳排放量基本稳定时,碳交易成本与价格呈正相关,交易价格增加到一定程度后,基于综合成本考虑,系统调度转向低排放机组,此时碳排放量显著降低,交易成本也减少。随着交易价格继续增加,由于容量及负荷需求限制,当EB 与GB利用率稳定后,系统碳排放量稳定在较低水平,此时交易成本与价格呈正相关。即碳交易价格的改变可以有效实现系统运行的经济性和低碳性之间的协调与均衡,碳价波动能显著影响系统碳排放量。

4.5.2 区间置信度分析

区间预测的置信水平反映了调度决策对系统运行可靠性要求,本文分析了不同置信水平提取的系统电负荷需求,如图4 所示。

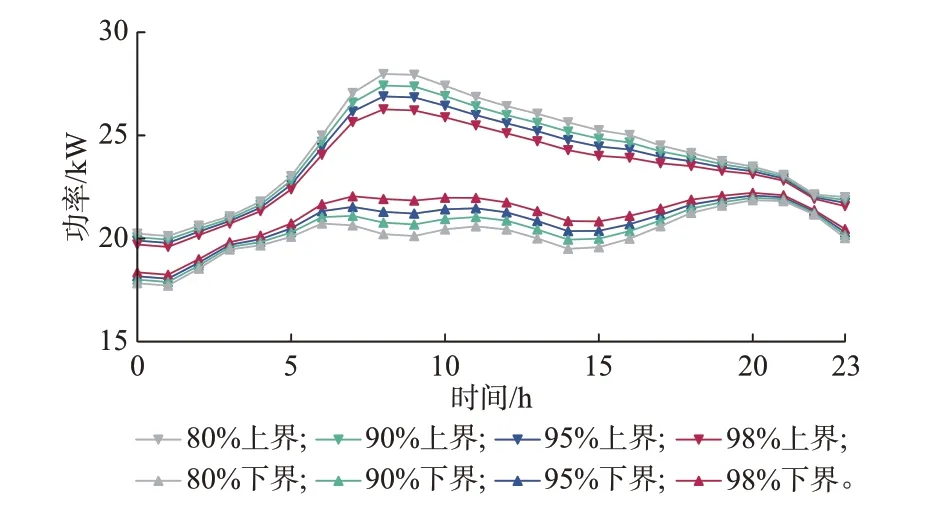
图4 不同置信度下的系统电负荷需求Fig.4 System electrical load requirements at different confidence levels

由图4 可知,置信度取98%时能保证所提取区间的全面性,但区间范围较大,在实际应用中容易造成干扰。

为明确建模中考虑多重不确定性的意义,将不同置信度下各调度目标及算法效率提取的区间变量代入模型优化,结果如表5 所示。

表5 不同置信度下的调度结果对比Table 5 Comparison of dispatch results at different confidence levels

随着置信区间的减小,运营成本的上下限逐渐减小；同时,综合成本的平均值随之减小,区间范围不断缩小。当不确定性增加时,算法求解时间有所增加,但仍在可接受范围内。在实际调度策略中,可以灵活调整不确定性参数,改变调度方案的保守性,以满足不同调度用户的风险偏好。另一方面,综合考虑系统不确定性影响能避免对最恶劣情况的过度估计,改善传统方案的保守性,提高调度互动灵活性,并一定程度降低调度成本。

5 结语

本文建立了不确定性建筑能量管理系统模型,考虑各类不确定因素,计及系统用户对于运行经济性及人体舒适度的要求,对智能建筑优化调控模型进行求解,算例仿真结果表明:

1）基于深度强化学习的IMOPSO 算法利用DQN 与IMOPSO 交互,学习建筑模型状态、动作、奖励间的隐式关系,进而指导区间种群运动,可以实现Pareto 前沿的快速逼近与区间收敛。求解得到负荷动作策略区间,将优化决策由点拓展到区间,克服了传统确定性方法以点代面的分析思想,提高了调度互动的灵活性。

2）随着置信区间的减小,运营成本区间与综合成本区间均会缩小,在置信度区间为80%时,成本运行区间为98.02 元,占成本区间均值的6.62%；置信度区间为98%时,运行成本区间宽度增加155 元,占成本区间均值上升到9.69%。随着不确定性程度增加,调度方案的保守性风险增大,降低不确定性能够提高调度互动的灵活性,并一定程度降低调度成本。

需要指出的是,本文在负荷动作空间的取值上进行了离散化处理,基于深度强化学习算法的变量连续性问题仍有待优化。同时,所考虑的系统用能需求不够全面,包含电负荷、热负荷、氢负荷及气负荷等用能需求的综合能源系统协同优化有待进一步研究。

本文仅初步探索了将深度强化学习融入多目标区间优化的一种方式,如何比较不同强化学习的模型动态指导能力,以及如何深度耦合优化算法,将成为下一步工作的研究重点。

本文研究得到深圳市科技计划（JCYJ20210324131409026）、国网湖北省电力 有 限 公 司 2022 年 科 技 项 目（521538220005）资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。