时变载荷下三维摩擦系统接触运动响应研究

周耀兵，雷 威，何思澈，郭子源，赵 灯*

（第二船舶设计研究所，湖北 武汉）

引言

冲击是机械系统中遇到的强非线性行为之一，由于其在齿侧间隙、悬架系统、转子轴承系统等齿轮啮合系统的建模中被广泛研究。力-位置关系的固有非线性引起了丰富的非线性现象，包括擦掠分岔和混沌运动，相关的研究一直备受关注。例如，Dyskin 等人[1]考虑了具有完美弹性接触和周期性驱动力的冲击振荡器，发现次谐波共振的振幅比线性增长慢。Jiang 等人[2]发现，当单面冲击振荡器的刚度比随着弹性约束的增加而增加时，会出现从光滑分岔到非光滑分岔的转变现象。

同时，摩擦是两个接触面产生的涉及相对运动的对抗性力，由于表面磨损和能量耗散是大多数机械系统在设计和工作过程中关注的两个主要问题，因此在文献中也得到了相当大的关注。涉及摩擦界面的动力学问题在广泛的技术和科学应用中被发现，包括螺栓连接、涡轮叶片、铁路转向架以及许多其他。对于更复杂的二维问题，相对简单的系统可以表现出复杂的不稳定性，对运动方程进行精确的数值积分就会出现问题。Menq[3]给出了二维库仑摩擦系统中不包含滑/粘转移的质点的一项简谐形式解析解。

为了代表齿轮轴承系统、BHA 等面向工程的问题，本文建立了一个包含碰撞和摩擦的二维摩擦系统的数值算法来研究其动态响应，拓展了在恒定外部激励作用下的平面滑移过程中质量所走曲线长度的闭合形式解，并根据滑动曲线长度预测冲击位置。在此基础上，提出了一种二维摩擦系统曲线长度封闭解的求解算法。

1 三维单节点摩擦模型

如图1 所示，在二维摩擦系统中可以将滑块载荷简化为集中力Qt以及摩擦力Fμ，其中摩擦力与正压力和速度有关，集中力受到阻尼、刚度、外部激励等控制。

图1 二维摩擦系统

在以往的研究中，作者已经提供了二维摩擦系统数值解析解，如下式所示。

1.1 滑移-黏附转换

考虑到集中力Qt以及摩擦力Fμ之间的相互关系，滑移-黏附转换可以细分为滑移→黏附转化和黏附→滑移转换。而转换过程最重要的特征为转换时间以及转换位置。

在滑移→黏附转换过程中，当速度将为零瞬间，集中力Qt与速度之间的夹角，因此，转换时间和黏附前瞬间滑移轨迹可以表述为:

在黏附→滑移过程中，利用对运动方程进行泰勒展开，可以获取时间间隔内滑块的运动响应如式(3)所示。

1.2 滑移/黏附-分离转换

当法向力N 能够克服自身重力时能够使得滑块与接触平面发生分离，此时摩擦力为零，因此=0。因此，滑移→分离前滑移轨迹可以表述为

对于平面接触模型，只要滑块运动纵坐标满足z>z0，滑块将一直处于分离阶段。考虑到滑块与接触平面碰撞时会引起速度突变，造成能量发生损耗，因此碰撞后滑块运动状态与滑块运动速度有关，如式(5)所示。

2 案例与验证

为了进一步验证上述接触解析解，本文综合考虑了刚度和阻尼引入了如式(6)所示的集中力形式

2.1 滑移-黏附转换

为了在运动过程中引入滑移-黏附转换，本文将式(6)中各参数设置为。在法向力N 小于重力的情况下，在运动过程中不可能产生滑移/黏附-分离转换，而集中力与最大摩擦力Fμ之间的大小关系未定，使得在运动过程中滑块能够与接触平面保持接触状态，同时引?入了滑移-黏附转换。

动态响应和状态转换时间可以用来评价我们所提供的摩擦算法和另外两种数值方法(数值积分法NI和龙格-库塔法RK)。

图2(a)展示了在式(6)所示的外部受力条件下结点在达到稳定运动后的运动轨迹变化。在一个运动周期内，结点存在两处速度响应变化剧烈位置，对结点运动响应精确求解提高了难度。

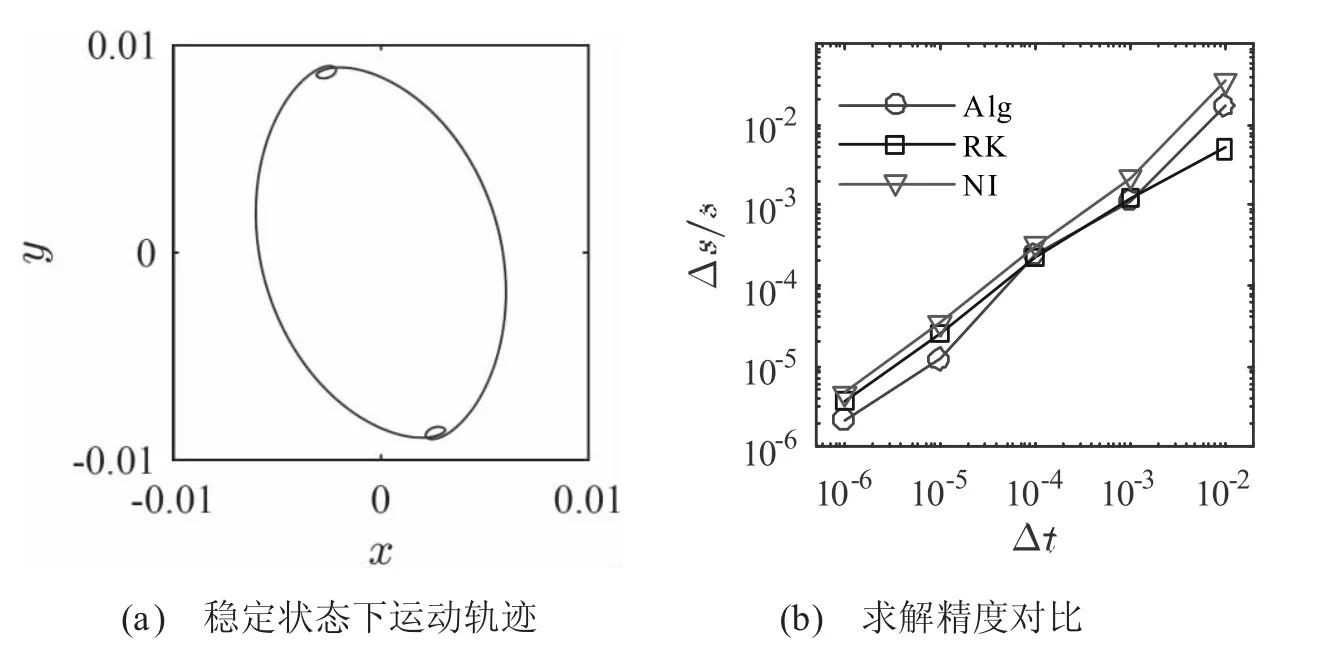
图2 滑移- 黏附转化结点运动响应

图2(a)比较了使用本文的求解算法（Alg）、数值积分法（NI）和龙格-库塔法（RK）在时间步长△t=10-5下节点稳定运动轨迹。结果表明，基于三种求解算法的运动轨迹完全重合，本文提出的求解算法能够准确地计算动力响应和预测滑粘过渡。

为了进一步验证该算法对求解补偿的敏感性，本文采用一系列的时间步长，对三种求解算法的求解结果进行了对比。如图2(b)所示，展示了五种时间步长下20 s 时刻的节点位置误差。由于数值计算的准确性与时间离散负相关，时间步长越小，求解结果愈接近于准确解。因此本文拟定△t=10-8条件下可以获取节点运动的“准确值”。如图2(b)所示，可以明显看出三种不同算法下在对数坐标系中节点位置误差与时间步长近似呈现线性相关。NI 算法由于只能通过节点运动数据实时判定节点的当前运动状态，而且在一个时间步内忽略了节点运动过程中外部在和的变化，为求解计算引入一定误差，因此在三种算法中NI 算法的求解准确性最弱。RK 算法在时间步长较低时求解准确性最好，而随着时间步长降低，节点位置误差会逐步向NI 接近，求解准确性将弱于本文提出的求解算法。本文提出的算法充分考虑了节点在运动过程中状态转变阶段，以及在同一个时间周期内因运动方向的改变引起的摩擦力变化，能够更加准确预测节点的运动轨迹。

2.2 滑移/黏附-分离转换验证

为了在运动过程中产生滑移/粘连分离过渡，将选择式(5)中的参数An的值为An=12，以确保单节点接触可以违反不等式Q0<μmg。图3 对比了三种方法计算出的运动平面的状态转换力矩、轨道和速度。我们可以发现，当单个节点的法向坐标低于零时，由于受到界面的冲击，速度会发生突然的变化，甚至Vx和Vy也会减小到零。这意味着单个结点在整个运动过程中可以经历滑动分离和黏附分离的转换。因此，利用我们的摩擦算法能够准确地预测具有单节点接触的三维摩擦系统中时变外部载荷下涉及滑移-粘连-分离过渡的动力学响应。

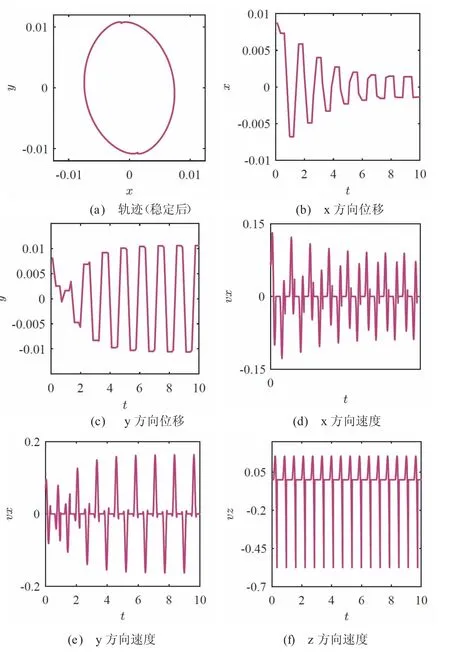
图3 滑移/黏附- 分离转化结点运动响应

如图3(b)-(c)所示，在周期性外部载荷作用下，节点运动轨迹在10 s 内逐渐达到稳定，最终呈现周期性运动，其稳定后的运动轨迹如图3(a)所示。如图3(d)-(f)所示，在运动过程中节点在三个方向上分速度均出现为零的情形，且出现时刻并不完全一致，可知在运动过程中节点发生了滑移-分离-黏附转换。在z 方向速度发生突降为零时，x、y 两方向的速度随着发生突变，可知此时节点与边界发生碰撞，引起了速度的突变，造成了能量损耗，发生了分离-滑移/黏附转变。

3 结论

为了求解二维摩擦系统动力学问题的数值解，提出了一种新的实现角增量的摩擦算法。结果表明，所提出的摩擦算法能够准确地捕捉到物体状态变化时的过渡时间，计算精度高。

研究结果为研究二维多节点系统中各节点的响应提供了基础，该系统中每个节点都涉及复杂的滑/粘转换，方便了复杂的多节点计算，它也可以推广到粗糙表面之间接触特性的研究。