复杂变时滞作用下的钻头纵扭耦合非线性振动*

2023-11-18侯祥雨刘显波龙新华蔡国平孟光

动力学与控制学报 2023年8期

侯祥雨刘显波† 龙新华蔡国平孟光

(1. 上海交通大学船舶海洋与建筑工程学院,上海 200240)(2. 上海交通大学机械与动力工程学院,上海 200240)

引言

钻柱系统是石油、天然气资源开采过程中的核心组件,是一个具有超大长径比的柔性旋转机械系统.由于大柔性结构具有刚度低、模态密集、阻尼小以及几何非线性明显等特性[1],在钻井过程复杂的力学环境下,钻柱系统极易发生动力学失稳并产生具有危害性和破坏性的自激振动[2-3].因此,如何准确建立钻柱动力学模型以及描述钻井破岩过程中的非线性关系,是钻井工程领域长期以来高度重视并亟待解决的问题.

针对钻柱的动力学问题,国外一些学者展开了大量的实验研究.Finnie与Bailey[4]首次对钻柱振动进行了实验研究,通过实验装置实现了对钻柱顶部旋转运动、轴向运动、扭矩、以及轴向拉力的测量与记录,首次观测到了钻柱运动中存在的多种形式的振动,特别是发现了其中存在大量的扭振成分.滕学清等[5]采用ESM钻柱振动测量工具测量了某超深井井下钻柱的三轴加速度,分析表明实测井段发生了大量的粘滑振动.

此外,针对钻井破岩过程的时滞效应,D. Dareing等[6]最早于1990年首次引入钻头的再生切削效应,并得到了线性定常时滞下钻柱的动力学稳定性,但未考虑钻头的扭振,与实际钻柱系统相差较大.2004年,Richard等[7]首次考虑了纵扭耦合运动,提出了状态依赖型时滞问题,并考虑了干摩擦、钻头跳起的非光滑效应,建立了钻柱的时滞-非光滑动力学经典模型.

近年来,Liu等[8]提出了变时滞、非光滑作用下的8自由度纵-横-扭耦合缩减模型,发现系统在时滞与非光滑作用下存在的多处黏-滑振动、钻头跳起与碰撞等现象.随后,对纵扭耦合的状态依赖型时滞系统的稳定性进行了半离散求解,在三维的参数空间得到了稳定包络面[9].Liu等[10]采用集中质量方法,首次研究了钻柱系统的有限元模型在状态依赖型时滞作用下的稳定性,得到了与低自由度缩减系统完全不同的稳定区域.

与此同时,钻头破岩动力学相关的时滞系统建模、算法等方面也取得了较大进展.Nandakumar等[11]对状态依赖型时滞提出了伽辽金法,将状态依赖型时滞微分方程转换为有限个常微分方程的形式,从而方便采用通用非线性分析方法对非线性时滞系统进行研究.Wahi等[12]提出了以偏微分方程的形式取代时滞微分方程,从而对非连续非光滑引起的多重再生效应进行准确建模.Liu等[13]用偏微分方程描述时滞过程,发现对于定常时滞的单自由度切削系统,由于切削刃的跳离,将会变成倍时滞问题,且倍数取值与相对振幅(振幅与名义切削厚度比值)呈正相关,时滞的跳变使得系统的动力学特性发生根本性改变并产生了复杂的混沌、超混沌现象.张鹤等[14]给出了考虑钻头纵扭耦合的状态依赖时滞微分方程,并利用谱方法和伽辽金方法分析了系统的线性稳定性.需要注意到,实际钻井作业中,钻头的振动幅度远大于名义切削厚度,这将导致钻井过程的钻头跳起更为普遍,时滞跳变也更为剧烈.为此,Liu等[15]基于钻井作业中钻头-岩层切削界面的实际工况,提出了“复杂时滞”概念,即时滞量的大小不仅连续波动变化,还会产生剧烈跳变的现象,该复杂时滞的引入,完善了钻头-岩层界面的动力学模型.

总体而言,围绕钻柱系统建模、非线性动力学、时滞系统稳定性分析多方面内容,虽然国内外已取得了一些显著成果,但对于许多问题的探讨仍处于初步阶段,有待进一步深入研究.为此,本文的主要研究包括以下几方面:首先是钻头-岩层界面由于多重再生切削效应引起的复杂变时滞问题的建模与求解;其次,将通过半离散法,对钻柱纵-扭动力学失稳规律及机理进行分析;最后,基于边界控制的思想,通过对顶部的柔顺边界参数进行优化,实现对稳定钻井工作参数包络线的拓展.

1 考虑复杂时滞的钻柱动力学建模

如图1(a)所示的典型陆上垂直钻井系统,其中钻柱总长度1200米,包括1000米的钻杆、总长200米的钻铤以及钻头所组成的空间连续的柔性转子系统,置于直径略大于钻头的圆柱形井壁导管中,导管和钻柱之间流有钻井液,起到对井底进行冲洗、冷却,并将泥浆返回地面的作用.其中钻柱钻进速度为V0,顶驱以恒定转速Ω0驱动整个钻柱系统.图1 (b)为考虑钻柱纵扭耦合的连续体动力学模型,是对图1(a)所示的钻井系统的简化,考虑了钻柱结构本身的阻尼和钻井液的粘性阻尼以及浮力和重力等外部载荷等因素.但为了深入研究顶部边界和复杂钻头-岩层切削界面等边界条件对钻头运动的影响,对图1 (b)连续体系统做进一步缩减,即将钻杆、钻铤和钻头的质量一同集中在系统底部,缩减为集中质量圆盘,通过弹性阻尼元件与顶驱相连,如图1 (c)所示.

图1 钻柱系统及其动力学模型Fig.1 Schematic of a drilling system and its dynamic models

1.1 考虑柔顺边界的钻柱结构动力学缩减模型

相比以往研究中采用固定转速或者恒定驱动力矩的边界条件,本研究采用了更为一般的边界条件.考虑目前商用顶部驱动机构(顶驱)具有的可调刚度与可调阻尼,以及顶驱自身的转动惯量I1,扭转运动的顶部边界可以建模成更为一般的惯量-弹簧-阻尼系统.同理,考虑顶部吊塔悬挂刚度与阻尼,顶部机构质量M1,纵向运动也可建模成更为一般的质量-弹簧-阻尼系统.

分别在顶驱和底部集中质量圆盘静力平衡位置处建立坐标系,如图1(c)所示,坐标变量x1和φ1分别描述顶驱到顶部(地面)的距离和扭转角位移,坐标变量x2和φ2分别描述底部圆盘的纵向位移和扭转角位移.根据牛顿第二定律,可得顶驱的动力学方程

(1)

(2)

式(1)中,Q和P分别包含了由于顶驱存在钻进速度V0和恒定转速Ω0产生的作用力和力矩,具体可表示为

Q=ka1V0t+ca1V0P=kt1Ω0t+ct1Ω0

(3)

类似的,底部圆盘的动力学方程

(4)

(5)

考虑浮力作用,并假定钻柱内外的钻井液压强一致,故式(4)中,在重力项M2g前添加浮力减轻系数b,一般典型的水基钻井液,可取b=0.873.

式(4)中,Wb和Tb表示作用于钻头的钻压和钻矩,具体形式见1.2节.

结合以上公式,将系统动力学方程整理成如下矩阵形式

(6)

式中,位移列阵z=[x1,x2,φ1,φ2]T,质量阵M=diag[M1,M2,I1,I2],刚度阵K、阻尼阵C和力阵Q具体形式如下

(7)

(8)

(9)

1.2 钻头-岩层界面建模以及“复杂时滞”的概念

钻井作业中,钻头(包括刮刀钻头、PDC钻头等)破岩过程如图2所示,作用于钻头的钻压Wb与钻矩Tb可由钻头-岩层切削界面力学模型得到.根据以往模型,钻头-岩层切削界面的作用力(矩)可分解成切削分量与摩擦分量,写成以下形式

Wb(t)=Wbc(t)+Wbf(t)

Tb(t)=Tbc(t)+Tbf(t)

(10)

式中,Wbc与Tbc即为切削力(矩)分量,而Wbf与Tbf即为摩擦力(矩)分量.其中,切削分量与钻头刃齿的瞬时切削厚度成正比;摩擦分量则与岩层强度及刃齿几何相关,而与切削厚度无关.

在实际钻井中,考虑非线性因素:例如钻头纵向振动跳起引起的钻头-岩层界面分离、钻头大幅扭转振动引起的黏滑运动甚至钻头反转,上式中钻压Wb与钻矩Tb的四个分量可以写成如下非线性函数形式

(11)

式中ε为与岩层强度相关的力学参数.σ,ζ,a,μ,γ为钻头-岩石接触界面相关的力学参数,以上参数均列于附录变量表中.标量函数R(·)、H(·)、sgn(·)分别为斜坡函数、单位阶跃函数、以及符号函数,此类函数将为系统引入非连续、非光滑的强非线性.

式(11)中变量dN(t)为钻头所有刃齿瞬时切削厚度总和.对于具有N组刃齿的PDC钻头或刮刀钻头,钻头的瞬时切削厚度总和dN及每刃切削厚度分别为

dN(t)=Nd(t)

d(t)=x2(t)-x2(t-τ)

(12)

上式描述的切削厚度计算方式,即钻头刃齿的瞬时切削厚度不仅与当前钻头刃齿位置状态有关,也与之前一个刃齿的位置相关.其中,τ=τ(t)为时滞变量,在不考虑跳钻的情形下,根据以往研究,时滞大小等于钻头旋转一个刃齿角度2π/N所需的时间,由于扭振导致转速的波动,时滞τ也将发生波动,可以写成以下变量φ2(t)的隐式函数形式

(13)

该隐函数方程可通过数值求解得到,在运动方程的时域数值仿真的每一次迭代中,均需要数值求解一次该隐函数方程.由于该方程没有考虑钻头跳起的强非线性,最终得到的时滞τ=τ[φ2(t),t]将为一条光滑的关于状态变量φ2的函数曲线[图11(a)],以往研究中采用的状态依赖型时滞即为该类型时滞.

然而在实际工况中,钻头刃齿跳离岩层的情况极易发生.由于切削界面分离,瞬时切削厚度将与之前的多个刃齿位置相关,即在定转速的车削、铣削动力学中的多重再生切削,使得时滞量发生整数跳变.而钻井过程由于转子的扭转大柔性以及钻头的纵向跳钻,时滞的求解需要同时考虑多重再生效应导致的倍时滞跳变以及扭振导致的时滞波动,我们称此时滞为“复杂时滞”[图11(b)].为此我们考虑多个刃齿周期前的钻头位置,将式(13)进行拓展,得到以下多个关于时滞的隐函数方程

(14)

式中Nr为求解过程中设置的最大再生数,求解过程中需设置到足够大(例如Nr=20).在求解以上Nr个方程之后,瞬时切削厚度(每刃)可以写成如下形式

(15)

式中min(·)为最小值函数(当i=1,2,…,Nr时).如图3所示,当前的最小切削厚度是由刃齿的当前位置以及2个刃齿以前的轨迹位置决定,i=2时上式取得最小值,即为2重再生切削.

对于具有剧烈振动的强非线性钻柱动力学问题,精确的数值仿真对Nr的选取理论上需要包含所有的刃齿轨迹.而在实际应用中,Nr的选取可以根据钻头纵向的相对振动幅值来大致给定.本研究中仿真选取Nr=30以保证数值仿真的精确性.此外,以上提出的复杂时滞模型通过设置Nr=1即可向下兼容以往状态依赖型时滞模型.

同时,为平衡计算精度和计算时间,本文复杂时滞采用快速递归算法进行求解(具体求解步骤见以往研究[15]).

图3 钻头运动轨迹的岩层表面展开及多重再生切削效应示意图Fig.3 Schematic of rock surface unfolding of drill bit motion trajectory and multiple regenerative cutting effect

2 考虑顶部边界的钻柱破岩稳定性研究

2.1 钻头破岩动力学稳定性判据

对于动力学方程,其存在一个平凡解,即系统以名义参数钻进的平衡位置,该平衡位置可能是稳定的也可能是不稳定的.对于平凡解,式(11)中的非光滑函数的自变量都为正,时滞和瞬时切削厚度均为常数,可以整理成下式

(16)

(17)

(18)

由式可知,位移向量zs随时间线性增长,常数向量Uss为钻柱的纵扭两个方向上的静态变形场向量,它是由稳态的重量、浮力、钻压、钻矩以及外部阻尼力(矩)等引起的.

若考虑钻头-岩层的切削界面所受到的时滞效应,系统的平衡位置,即上述平凡解:式(16)～(18),容易发生自激振动而失稳,并在非线性的作用下引发有害的扭转黏滑振动与纵向的跳钻.为研究系统平衡位置稳定性,我们在平衡点附近做线性化,并将系统平衡位置平移到原点,则线性派生系统的位移向量可做如下定义

(19)

(20)

式中右边为线性化之后的钻压与钻矩,作用于钻头,EC具体形式为

(21)

式中,矩阵WC和TC分别是与钻头的切削受力相关的常数矩阵,具体形式为

(22)

钻柱动力学线性派生系统式(20)为线性时滞自治系统,其时滞量τs为常数,由钻头的名义时滞式(16)确定.

线性派生系统的稳定性可以由半离散法确定[16-18],首先将式(20)和式(21)写成如下状态空间的表达形式

(23)

(24)

式中的纵扭刚度矩阵Kat及阻尼矩阵Cat来自于钻柱结构刚度与阻尼.而时滞刚度矩阵Kτ则来自于派生系统的时滞项,分别由以下公式确定

Kat=M-1K

Cat=M-1C

Kτ=M-1EC

(25)

此时已得到了线性派生系统的状态变量形式的动力学方程,采用Insperger与Stépán的半离散法[16-18],时滞微分系统可以写成如下离散的迭代形式

Γi+1=DΓi,i=1,2,3,…

(26)

式中下标i代表了时间的离散坐标:t=iΔt,时间步长Δt=τs(m+0.5)中的正整数m则代表了半离散法的时间离散精度.此时,在第i次迭代时,离散状态变量Γi为8+2m维的列向量,写成如下形式

(27)

式中Γi后面的2m个状态变量则来自于对时滞的时间离散.显然时间离散精度由正整数m决定.式(26)中系数矩阵D,是一个和钻柱结构参数、钻头参数、岩层参数以及钻井作业参数都密切有关的矩阵.其可由半离散法确定[16-18],但限于篇幅,在此不做展开.

可以证明,在时间离散精度足够的情形下,式(6)的稳定性将趋向并收敛于时滞线性派生系统.由迭代法的收敛性判定条件可知,当系数矩阵D的谱半径小于单位1时,式(26)的迭代将是稳定收敛的,即系统稳定的判定如下

S(D)=max(|λi(D)|)<1

(28)

上式谱半径的求解涉及到式(23)～(27)的运算,涉及到了钻柱结构参数、钻头参数、岩层参数以及钻井作业参数,因此该稳定性判别式结合钻柱结构参数与钻井作业参数便可得到钻井作业在各种状态下的稳定性.

同时为方便后续稳定性研究,定义稳定性差值

s(D)=S(D)-1

(29)

则当s(D)>0时,系统处于不稳定状态,系统运动最终会失稳发散;s(D)<0时,系统处于稳定状态,系统运动最终会趋于稳定;s(D)=0时,系统则处于临界稳定状态.

2.2 动力学稳定性的参数研究

(1)转速与钻压参数的研究

通过求解线性派生时滞系统平凡解的稳定性,进而可确定钻井作业时稳态钻进过程的稳定性.由于该动力学稳定性与作业参数密切相关,而转速Ω0与名义钻压Wbs是进行钻井作业的两个重要参数,也是最需要控制的两个关键参数,钻柱系统稳定性的分析也将主要围绕这两个参数展开,其他参数的选取在没特殊说明情况下,参照附录变量表.

如图4所示,研究得到了不同参数平面下纵扭耦合的钻柱系统缩减模型的稳定性状态.图4(a)展示了钻速Ω0-名义切削厚度dNs平面下系统的稳定性,其中绿色阴影区域为稳定参数区域,白色区域为不稳定区.黑色实线为稳定性差值s(D)等高线,较粗实线为0,代表临界稳定性边界;较细实线代表不同的稳定性数值.该稳定性区域的求解是通过将图中Ω0-dNs参数平面划分成300×300的网格,采用每个网格的中心点所处位置的参数代入式(23)～(27)至分别进行稳定性判定,最后参数平面所有网格点的稳定性集合得到稳定性图.

通过图4 (a)可以看出,稳定钻进区域主要位于转速Ω0>135RPM的转速区域.在图中绿色阴影区域内的钻井作业参数,钻柱的小幅纵扭振动均会收敛而形成稳定的钻进过程,系统平凡解和是稳定的.与此相反,在不稳定区域,钻柱微小的振动将逐渐发散,形成幅度可观的纵扭耦合振动,例如黏滑运动、跳钻等.并且通过对比两条S(D)等高线和临界稳定性边界可以看出,减小名义切削厚度dNs和增加转速Ω0,都可以使系统进入稳定性区域,但增加转速,稳定性数值回落更快,即系统稳定性对转速Ω0更加敏感.

图4 不同参数平面下的稳定性Fig.4 Stability diagram in the space of different parameters

通过式(16)和式(18),可以将名义切削厚度dNs转化为名义钻压Wbs,即可得Ω0-Wbs参数平面下的系统稳定性,如图4 (b)所示.与图5 (a)相比,多出的浅绿色区域表示系统稳定,但钻头无法钻进岩层.同时,该参数平面的稳定性图还显示了随着转速增加,最大稳定钻压具有下降的趋势.

(2)岩层强度的参数研究

钻井作业时,随着井底钻头到达不同的岩层,钻头-岩层界面的切削力学参数将发生变化.图5分别展示了岩层强度参数ε在20MPa[图5(a)]、60MPa[图5(b)]和200MPa[图5(c)]变化时,钻柱稳定钻进的Ω0-Wbs参数区域.该稳定性图说明无论岩层强度变化,钻柱在低转速时总是不稳定的.同时,随着岩层强度的增加,为保持系统稳定所需的最低稳定转速不断提高;为保持钻头钻进岩层所需的最低稳定钻压也在不断提高.同时,在稳定区域,随着转速的增大,最大稳定钻压具有下降的趋势.

图5 钻柱缩减系统稳定性随岩层强度的变化Fig.5 The stability of drill-string reduction system changes with intrinsic specific energy of rock

值得注意的是,当岩层强度较小时[图5(a)],最大稳定钻压很小,导致稳定参数区域的面积很小.这是因为当岩层强度不大时,钻压过大会使钻头陷在岩层中,从而导致钻柱系统的不稳定.

(3)顶部边界的影响及稳定性优化

相比于以往研究中传统的恒定力及力矩边界(即自由边界)[7,19-22],恒定速度及转速边界(即固定边界)[8,10,16,23],本文采用了更通用的柔顺顶部边界条件,并且对不同边界条件下的钻柱缩减系统的纵扭耦合动力学方程的稳定性进行了求解与对比.附录表中列出了传统顶部边界条件下的顶部边界参数设置.

通过将顶部边界参数ka1,kt1,ca1,ct1均设置为0,即可得到自由边界下的钻柱稳定性,如图6(a)所示.通过设置ka1,kt1为无穷大,即可得到固定边界下的钻柱稳定性,如图6(b)所示.同理,通过设置各边界参数如附表所示,即可得到默认边界,此时的稳定钻井区域如图6(c)所示.以上稳定性图表明在传统边界条件下,系统钻进保持稳定的最低转速

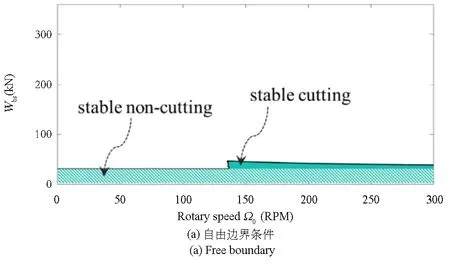
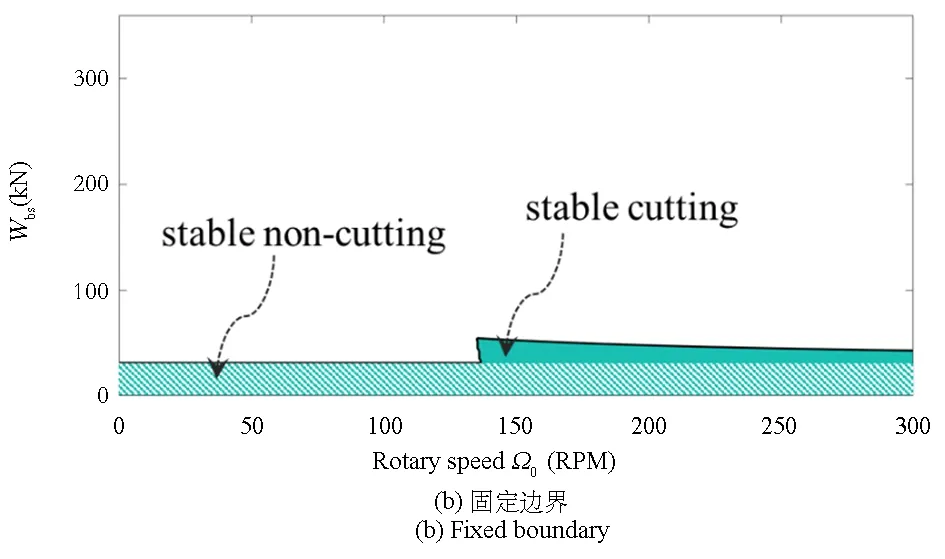
相同,约为140RPM,最高稳定钻压也相差不大,使得稳定钻进的参数区域面积都很小.图6(d)展示了在优化的柔顺边界下,钻柱缩减系统的稳定性.其中优化边界的参数选取遵循文献[24].结果显示,具有质量、刚度、阻尼的一般边界条件可以扩大钻柱稳定工作参数区域,这是由于该边界的柔性与阻尼可以对传导至顶部的钻柱振动进行部分吸收.图6的稳定性结果对比说明钻柱顶部边界对钻柱稳定性有重要影响,可以通过优化边界条件,抑制钻柱振动,提高钻井作业的稳定性.

最后需要指出的是,以上的参数空间稳定性分基本是在驱动转速Ω0和钻压Wbs张成的参数平面进行的.该稳定性图也可以依据式(18)中Wbs(Ω0,V0)的变化方式,变换到转速与钻速的参数平面[(Ω0-V0)平面].

3 钻柱纵扭耦合非线性振动时域特性分析

3.1 复杂时滞与非光滑作用下的钻柱纵-扭耦合振动特性

本节主要研究复杂时滞作用下钻柱的非线性动力学行为,采用时域数值方法,对纵扭耦合的钻柱缩减模型进行仿真与分析.

(1)钻柱稳定性的时域数值仿真验证

Ω0-Wbs参数平面下,参数点选取及参数坐标如图7所示,其中参数点a在临界稳定性边界上,参数点A、B、C位于边界线外侧,为不稳定平衡点,参数点b、c位于边界线内侧,为稳定区域.

图7 参数点选取示意图Fig.7 Schematic of parameter points

各参数点的稳定性时域数值仿真如图8所示,图中蓝色曲线为顶部驱动的扭转速度,橙色曲线为井底钻头的扭转速度.当取值点为点A、B、C时,顶驱和钻头的运动最终都失稳发散,如图8(a)、(b)和(c)所示;当取值点为点a、b、c时,顶驱和钻头的运动最终都趋近于稳定收敛,如图8(d)、(e)、(f)所示,这与上文对系统稳定性的结论一致,即当系统的钻速和钻压取值在临界稳定性边界上及以内时,系统的运动可以稳定收敛;反之,发散.

同时注意到,当参数穿越上边界失稳时(c→C),引起的系统发散速度较慢;而在左边界失稳时(b→B),发散速度较快,更容易形成具有危害性的黏滑振动,这也验证了上文对等高线的分析.

图8 各参数点(图4中)的稳定性时域数值仿真验证,(a) 参数点A,(b) 参数点B,(c) 参数点C,(d) 参数点a,(e) 参数点b,(f) 参数点cFig.8 Numerical simulation verification of stability time domain for each parameter points (Fig.4), (a) parameter point A, (b) parameter point B, (c) parameter point C, (d) parameter point a, (e) parameter point b, (f) parameter point c

(2)黏滑振动与钻头跳起

选取不稳定平衡点进行时域仿真,对钻头的黏滑振动与跳钻现象进行辨识和分析.当ε= 60MPa,转速Ω0=60RPM和钻压Wbs=36.5kN时,得到的系统运动曲线如图9所示.图中蓝色曲线为顶部驱动的运动速度(钻速与转速),橙色曲线为井底钻头的运动速度(钻速与转速).图9(a)显示顶驱和钻头的纵向运动具有准周期运动的特征,顶驱运动较为平稳,振速幅值也很小.相比顶驱,钻头的纵向运动在井底形成了小幅的黏滑运动,但尚未出现明显跳钻现象.

图9(b)显示在顶驱(蓝色曲线)基本以恒定转速驱动的情景下,井底钻头出现了较为明显的黏滑运动.在黏滞状态,钻头的转速为0,由于钻柱顶部仍以恒定转速驱动,此时由钻柱简化而来的弹性元件开始积蓄扭转弹性能.随后,在滑动状态,弹性元件释放弹性能,钻头高速旋转,其转速达到名义转速的2倍.黏滑运动是钻头刃齿脱落以及钻柱疲劳破坏的重要原因,在工程应用中需要尽量避免.当ε=60MPa,转速Ω0=60RPM和钻压Wbs=59.2kN时,得到的顶驱和钻头的运动曲线如图10所示.图10(a)显示,在该参数下,顶驱和钻头运动具有混沌

图9 钻头黏滑振动,ε= 60MPa,Ω0=60RPM,Wbs=36.5kN :(a) 纵向黏滑振动,(b) 扭转黏滑振动Fig.9 Stick-slip vibration of the drill bit, ε=60MPa,Ω0=60RPM,Wbs=36.5kN :(a) Axial stick-slip vibration,(b) Torsional stick-slip vibration

图10 钻头纵向跳起与扭转黏滑振动,ε=60MPa,Ω0=60RPM,Wbs=59.2kN :(a) 钻头纵向跳起,(b) 扭转黏滑振动Fig.10 Drill bit axial jump and torsional stick-slip vibration, ε=60MPa,Ω0=60RPM,Wbs=59.2kN :(a) Drill bit axial jump,(b) Torsional stick-slip vibration

特征.其中顶驱的振速幅值相对较小,但振动频率较高.钻头的纵向速度在-0.20m/s至0.35m/s之间波动,较(a)的振速幅值有所增加,且出现了速度为负的现象,即钻头跳起与岩层分离,这会导致多重再生效应,引起倍时滞跳变,造成系统的强非线性,不利于系统稳定.图10(b)显示,顶驱的扭振逐渐发散,且扭振振幅越来越大,扭振频率越来越高.与此同时,井底钻头出现了更为明显的黏滑运动,黏滞状态后的钻头高速旋转,其转速达到了名义转速的2倍以上.这种高频剧烈的黏滑振动更易造成钻头刃齿的脱落和钻柱的疲劳破坏.

(3)复杂时滞与传统时滞对比

选取不同参数进行时域仿真,对复杂时滞与传统状态依赖型时滞进行定量对比,如图11所示.参数为ε=60MPa,转速Ω0=60RPM和钻压Wbs=36.5kN时,时滞量随时间变变化如图11(a)所示,时滞量出现了0.2秒至1.0秒的大幅波动,但并未发生跳变现象,这说明,系统的纵向与扭转均出现了黏滑振动,但钻头与岩层并未发生分离,为连续破岩过程,即不存在多重再生效应.此时曲线显示,本研究提出的复杂时滞与以往研究中的状态依赖型时滞完全吻合.该状态下,复杂时滞的变化完全来源于转速波动,多重再生数nr=1,复杂时滞模型自动退化并兼容于以往的传统时滞.

图11 复杂时滞与传统时滞定量对比:(a) ε=60 MPa,Ω0=60RPM,Wbs=36.5kN,(b) ε=10 MPa,Ω0=40RPM,Wbs=120kNFig.11 Quantitative comparison of complex time delay and traditional time delay: (a) ε=60 MPa,Ω0=60RPM,Wbs=36.5kN,(b) ε=10 MPa,Ω0=40RPM,Wbs=120kN

参数为ε=10 MPa,转速Ω0=40RPM和钻压Wbs=120kN时,时滞量随时间变变化如图11(a)所示,本文采用的复杂时滞准确显示了时滞量的跳变与波动过程,而以往的状态依赖型时滞为连续波动的曲线.在该参数下,复杂时滞与以往的状态依赖型时滞产生了较大分歧,复杂时滞在某些情形下将跳到2倍值,说明此瞬时被切削岩层的上表面是由之前2刃齿所形成的;而某些情形时滞又降低到0,说明此瞬时钻头刃齿与岩层分离.此参数下系统多重再生数发生了周期-4的时变,即nr=1,0,1,2,1,0,1, 2….对应的最大多重再生数Nr=2.

3.4 基于边界参数优化的钻柱振动控制

分别在默认边界和柔性边界下,选取参数ε=60 MPa,转速Ω0=150RPM和钻压Wbs=96kN,进行时域仿真,验证边界参数优化后的钻柱振动抑制的有效性,分别如图12和图13所示.

图12显示,系统在默认边界下,顶驱(蓝色曲线)在经历一段暂态运动后,其纵向振动和扭转振动有逐渐发散的趋势,但总体振动幅值不大,可以忽略.而钻头的纵振和扭振较为剧烈,振动幅值首先逐渐增大,大概在140s后,运动趋于稳定的周期运动,其中图12(c)的相轨迹为极限环,也印证系统处于周期运动状态.

图12 默认边界下的系统时域仿真及相图:(a)纵向运动(b)扭转运动(c)钻头运动相图Fig.12 System time domain simulation and phase diagram under default boundary: (a) axial motion (b) torsional motion (c) phase diagram of drill bit motion

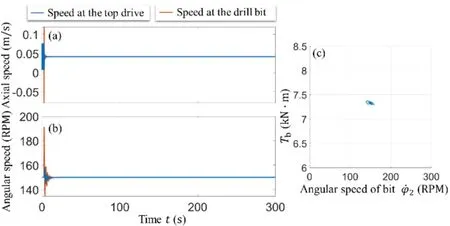
图13 柔性边界下的系统时域仿真及相图:(a)纵向运动(b)扭转运动(c)钻头运动相图Fig.13 System time domain simulation and phase diagram under general boundary: (a) axial motion (b) torsional motion (c) phase diagram of drill bit motion

相同参数条件下,对顶部的默认边界进行优化,取顶部悬挂刚度ka1=100kN/m,顶部悬挂阻尼ca1=3.8kNs,顶部旋转刚度kt1=10kNs/m,顶部旋转阻尼ct1=806kNs,得到的时域仿真及相轨迹如图13所示.可以明显看出,在经历一段暂态运动后,系统运动迅速收敛衰减,振动抑制明显.相轨迹[图13(c)]收敛于不动点.