基于流固耦合的介入机器人诊疗时血流动力学分析

朱宗铭 季苏强 王 浩 唐蒲华 梁 亮

1.长沙学院机电工程学院,长沙,4100222.湘潭大学机械工程与力学学院,湘潭,4111053.湖南师范大学工程与设计学院,长沙,410012

0 引言

区别于传统的血管介入手术,介入机器人可在血管内自由移动,并完成诊断血管、疏通血管和定点投药等工作[1]。血流动力学参数包括血流速度、血压、血流阻力(血管壁面剪切应力)等指标。血液在血管内流动时,血液流动和血管变形存在流固耦合效应。人们常引入计算流体力学、流固耦合等方法来预测血流动力学参数的变化。

血管内无介入装置时,国内外学者考虑流固耦合效应,对不同部位血管(胸动脉[2]、颈动脉[3]、椎动脉[4])、不同形状血管(直管[5]、弯管[6]和分叉管[7])和不同病变血管(含斑块[8]和囊肿[9])的血流动力学参数进行了数值计算和实验研究。

血管内存在介入装置时,血管的结构将发生变化,血液流动也随之改变。PEWOWARUK等[10]对导管介入前后的猪肺动脉分支狭窄模型中的血液动力学进行了数值模拟预测。JOHARI等[11]基于流固耦合效应,研究了专用支架植入颈动脉分叉血管后的管内血流动力学。DAI等[12]探讨了多个重叠非覆膜支架的孔隙率对主动脉夹层血流动力学的影响。WILLIAMSON等[13]采用粒子图像测速(particle image velocimetry,PIV)技术实验研究了主动脉髂分叉管中植入支架前后的分叉管近端和远端的血流动力学参数。江帆等[14]采用流固耦合方法,数值计算了弹性血管和刚性血管中介入机器人在固定位置旋转时的血流速度和血压等参数。LIANG等[15]研究了平移速度和转速等运行参数对刚性血管内运行的介入机器人综合性能的影响。

血流动力学研究分为血管内无介入装置和有介入装置两种。无介入装置时,考虑血管弹性(流固耦合作用)的研究主要涉及血管的部位、几何形状和病变结构。有介入装置时,研究主要涉及介入装置的类型(导管、支架、机器人等)、介入装置的运动状态(静止、旋转、移动等)、血管的力学性质(弹性和刚性)等。但针对弹性血管的研究未考虑介入装置的诊疗移动,针对介入装置移动的研究又假设在刚性血管内,即缺乏综合分析介入装置运动、血液流动和血管变形的耦合关系。本文基于血液和血管的双向流固耦合作用,对脉动血流环境中,介入机器人在血管内不同高度旋进诊疗时的血流特性开展数值计算和实验研究。

1 血管介入机器人的结构

介入机器人系统采用永磁体驱动,如图1所示,外部驱动永磁体为径向磁化的空心圆环。介入机器人外表面带有螺旋肋,内部有一个径向磁化的实心圆柱磁铁(与外部永磁体的异极相吸)。控制外部永磁体的平移和旋转(旋进)运动来驱动介入机器人做同样的旋进运动,清除血管内的血栓。

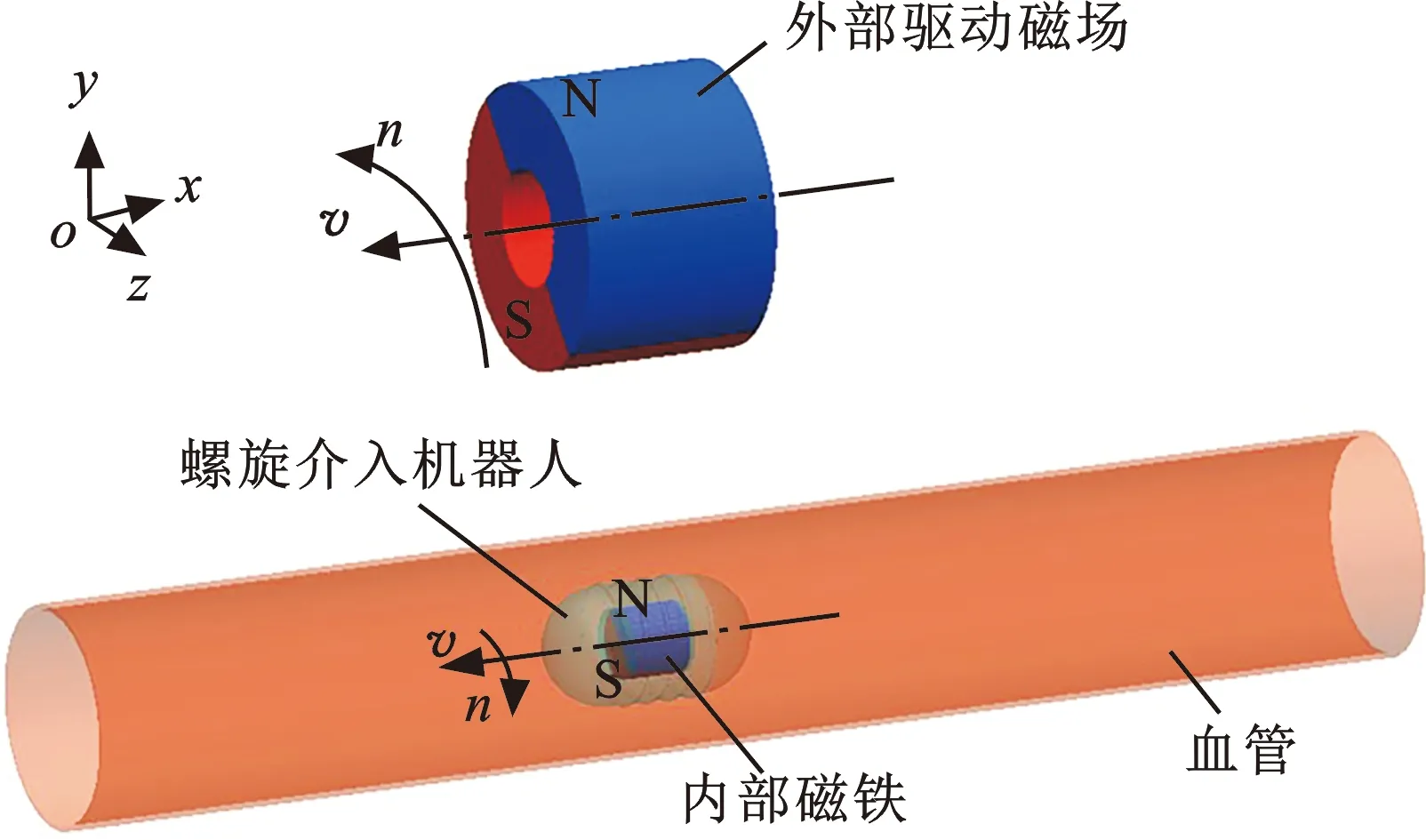
图1 血管介入机器人系统结构示意图

2 数值计算模型与方法

2.1 动力学控制方程

假设血液流体不受温度影响且不可压缩,则流体域控制方程包括连续性方程和动量守恒方程[16]：

(1)

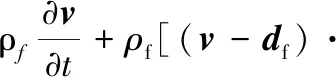
(2)

固体域控制方程可由牛顿第二定律导出:

(3)

式中,σs为血管壁应力张量;Fs为血管壁体积力;ρs为血管壁密度;ds为血管壁区域的局部加速度。

式(1)、式(2)为黏性流体动力学控制方程,式(3)为血管壁的固体控制方程,它们组成数值计算的数学模型。

在不考虑温度和热量影响的情况下,血液和血管壁耦合交界面处流体和固体满足

(4)

式中,σ为应力张量;n为边界法向向量;u为位移矢量;下标f表示流体,s表示固体。

2.2 系统建模

采用Pro/E软件建立包括机器人、血管和血液流体的介入机器人系统三维模型,相关参数见表1。为模拟机器人的运动,在机器人表面设计了一层包裹的流体(流体区域Ⅰ)。流体区域Ⅰ的厚度为0.5 mm。血管内剩余流体为流体区域Ⅱ。机器人系统的计算几何模型如图2所示。

表1 介入机器人系统相关参数

图2 血管机器人系统计算几何模型

2.3 网格划分

流固耦合过程中使用分区耦合算法计算,即流体域和固体域先独立计算,再进行数据交换,因此采用ANSYS-MESH模块对血管和血液进行网格划分。血管区域采用六面体结构网格Hex,默认单元尺寸为4.2426 mm。血液区域采用以四面体网格Tet为主、以楔形网格为辅的网格,默认单元尺寸为4.1976 mm。

流固耦合计算时,网格尺寸对计算结果和计算速度有较大影响。网格无关性分析的参考指标设为介入机器人运行时的血流出口平均速度。根据上述网格的划分方法,逐步对模型进行网格加密,并在其他参数相同的条件下进行数值模拟计算。采用不同网格数量的模型进行数值模拟,表2所示为网格数量与血流出口平均速度的关系,网格数量从387 904增加到632 711时,血流出口速度变化率(偏差)小于1%,满足网格无关性要求。综合考虑,选用第3组网格模型进行后续的数值模拟研究。

表2 网格无关性研究结果

2.4 双向流固耦合计算方法

介入机器人在血管中运行时,血管在流动血液的压力作用下产生变形,血管变形又会对血液流动造成影响,因此需构建双向流固耦合模型。

双向流固耦合研究中,流体区域(血液)和固体结构区域(血管)是并行求解的。每个子步骤中,流体域解和固体域解都需要收敛,才能继续下一个时间步长的计算,否则需要重新计算直至结果收敛。求解过程中,数据传递顺序如下:流体域将压力信息传递给固体域,固体域接收到压力信息后产生位移,位移引起计算区域发生变化,进而发生网格重构,之后,固体域再反馈给流体域。上述步骤完成一次即完成一个时间步长的计算,计算时间递增,直至达到计算周期结束,否则将固体域的位置与速度信息传递给流体域。双向流固耦合的计算过程如图3所示。

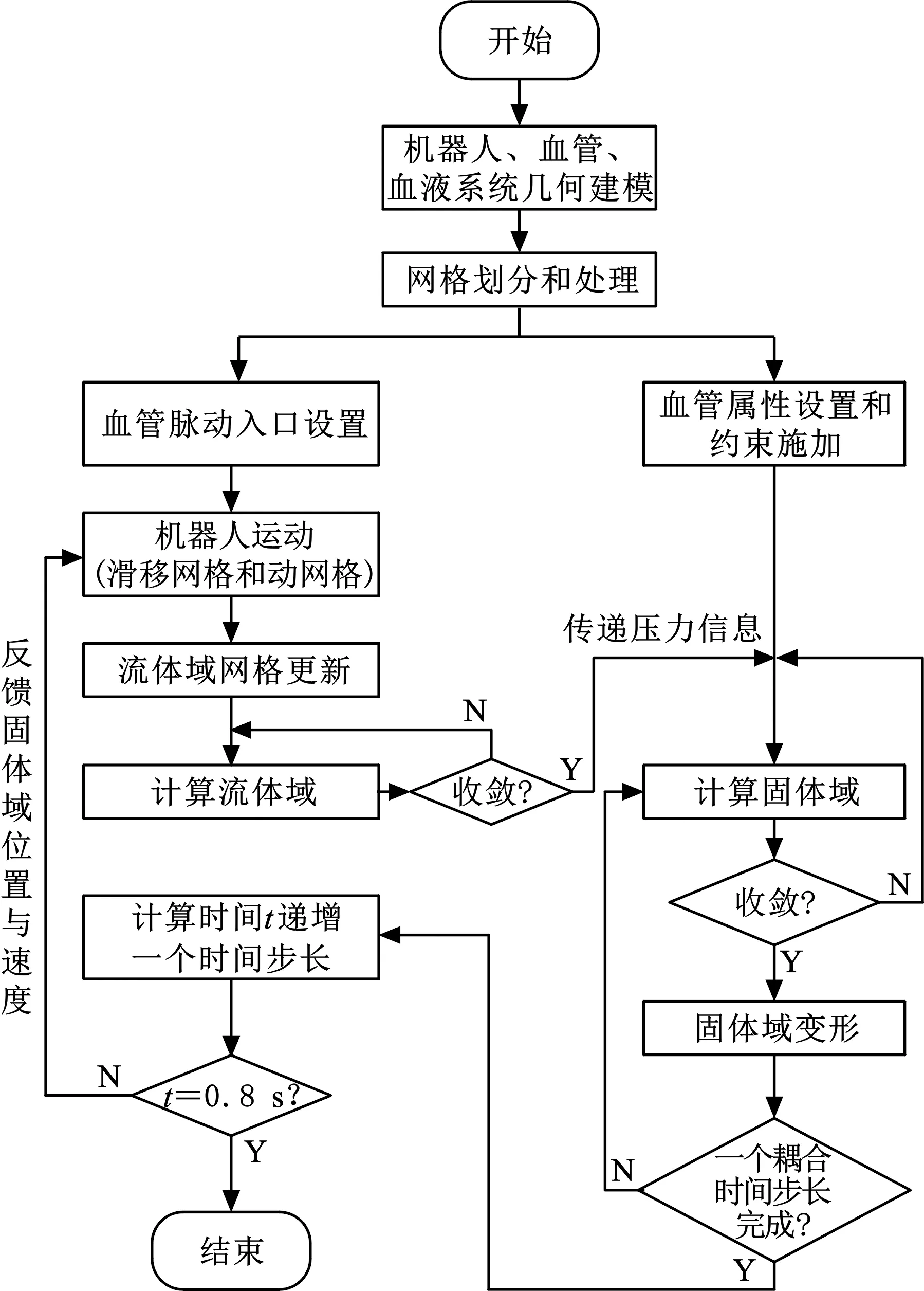
图3 双向流固耦合计算流程图

2.5 脉动血流入口条件和求解器参数设置

心房和心室规律性的收缩和舒张实现了间歇射血,使得动脉血具有显著的脉动特性。假设心脏搏动频率为每分钟75次,即心脏搏动周期为0.8 s。根据文献[17],采用图4所示的主动脉入口速度曲线拟合血流入口速度与时间的关系:

图4 主动脉血流入口速度曲线

vinlet=

(5)

采用用户自定义函数(userdefined function,UDF)编译脉动血流口速度条件,出口压力设为0。将血管的进出口端面定义为固定支撑。因为机器人的旋转运动,血管内流体的流动状态为湍流,故计算时采用标准k-ε湍流模型。设置湍流强度I为5%,水力直径D为18 mm。

根据实际情况,数值计算中设定机器人的平移速度vr为4 mm/s,运动方向与血流方向相反,机器人旋转速度nr为120 r/min。采用标准的SIMPLE算法求解流体压力和速度耦合方程,压力、动量、湍流动能和耗散率的差分格式均为二阶迎风格式。为模拟机器人表面邻近区域流体的运动,对机器人外层流体进行滑移网格设置,给定机器人外层流体转速等于机器人转速。

数值计算为非稳态计算,假定机器人沿着X轴正方向(图2)在管道内做旋进运动,其运动规律通过UDF控制。机器人移动和流固耦合作用导致的网格更新通过动网格重构实现。动网格区域创建中,流体与血管的交界面设定为系统耦合面,动网格重构时对邻近的边界层进行变形处理。系统耦合模块中,选择流体与血管的交界面为数据传输界面,其中,力传输的亚松驰因子设定为0.5。计算时间步长设置为0.01 s,计算结束时间为0.8 s。

3 数值计算结果与分析

机器人进入血管后,血液流动和血管变形都将受到影响,介入机器人在血管内不同高度运行时的血流动力学参数也将变化。假设血管中心轴的Y坐标为0,介入机器人在血管内5个不同高度(y1～y5)即机器人中心点的Y坐标分别为2.50 mm、1.25 mm、0 mm、-1.25 mm、-2.50 mm。

3.1 血流速度

图5所示为血流速度最大正值(t=0.25 s,收缩期内)时,介入机器人在血管内不同位置和无机器人介入时的血流速度流线,其中,血液从左侧入口流向右侧出口,机器人从右向左运动。由图5可知,t=0.25 s时,介入机器人在靠近血管壁时,血流速度略微增大,在血管中心的血流速度略微偏小,但总体差别较小,可见介入机器人高度对血流速度影响较小。血管内无介入机器人时,血流状态为层流,血管中心轴处的血流速度最大,为0.28 m/s,明显小于有介入机器人时的最大血流速度0.48 m/s。机器人的介入使得血管内径变小,血液流过机器人时,机器人周围流体域受到压缩,该区域血液流动速度增加,形成了高速流域。总体来说,不论介入机器人在血管哪个高度运行,血流速度均在人体的安全范围内,不会对血管造成损伤。

(a)机器人高度为2.50 mm

3.2 血压

图6为血流速度最大正值(t=0.25 s,收缩期内)和最大负值(t=0.45 s,舒张期内)时,介入机器人在血管不同高度和无机器人介入时的血液对血管壁压力(血压)分布图,可以看出,t=0.25 s时,机器人在不同高度的血压变化趋势大致相同:血管入口端的血压最大,并沿血流方向逐渐减小;血压最大值为120 Pa。无机器人介入时,血管内血压均匀变化,从入口向出口逐渐变小,血压最大值为72 Pa。因此,机器人的介入使血管内的血压变化不均匀,机器人周围的血压分布更复杂。收缩期内,机器人附近和血管末端会形成局部负压区。无机器人介入时,血流负压区仅在血管末端产生。在心脏收缩期,介入机器人在不同高度位置运行时,血压变化很小。

(a)机器人高度为2.50 mm(t=0.25 s)

t=0.45 s时,血液流动方向发生变化,部分血液回流,血压为负值(负压),血压绝对值从入口端向出口端递减。无机器人介入时,血压变化相对均匀,并且小于机器人介入的情况。介入机器人在不同高度的血压的最大负值和最小负值均相差较小。

因此,在心脏收缩和舒张期内,介入机器人在血管内运行高度的变化对血压影响均较小,且压力(-92 ～120 Pa)在人体安全范围内,不会对血管壁产生损伤,这说明介入机器人在血管内诊疗运行时是安全的。

3.3 血管壁面剪切应力

正常情况下,血液流动的剪切力对血管壁有益,能维持血管内皮细胞的功能。剪切应力过大或过小时,血管内皮细胞功能发生异常,影响血管壁的健康。因此,维持适当的壁面剪切应力对维护心血管健康至关重要。

壁面剪切应力与速度梯度有关,但较难通过临床直接测量获得。图7所示为一个脉动血流周期内的平均血管壁剪切应力-时间曲线。图7中,纵坐标为正值表示壁面剪切应力方向向右,负值表示壁面剪切应力方向向左。无机器人介入时,血管壁所受的最大剪切应力为0.076 Pa。血管壁面剪切应力长时间小于0.4 Pa会导致养分供给不足,使该区域易产生粥样硬化斑块。机器人介入后,血管壁面剪切应力明显增大,无论机器人在哪个高度运行,血管壁面剪切应力均在正常范围内波动,更有利于维持血管健康。

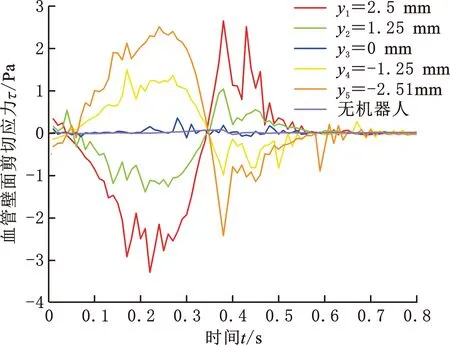
图7 平均血管壁剪切应力-时间曲线

由图7可以看出,介入机器人在不同高度的血管壁面剪切应力的变化趋势大致相同,并且与主动脉血流入口速度的变化规律基本一致。机器人越靠近血管壁,血管壁面剪切应力越大。因此,在机器人介入血管时,可调整机器人运行位置来改善壁面剪切应力以维持血管健康。

3.4 血管性质

上述研究考虑真实血管的弹性,采用流固耦合的分析方法,但血管性质对计算结果影响的大小如何,有待进一步分析。

表3所示为脉动血流收缩期内最大血流入口速度(t=0.25 s)时的血流动力学参数,可以看出,弹性血管模型下的最大血流速度、最大血压和血管壁面剪切应力均略小于刚性血管模型的结果。这是因为血管壁的弹性对血液流动起到一定的阻碍作用,使血流速度略微降低,导致血压和壁面剪切应力都减小。综合来看,考虑血管弹性的流固耦合计算结果更接近真实血管。

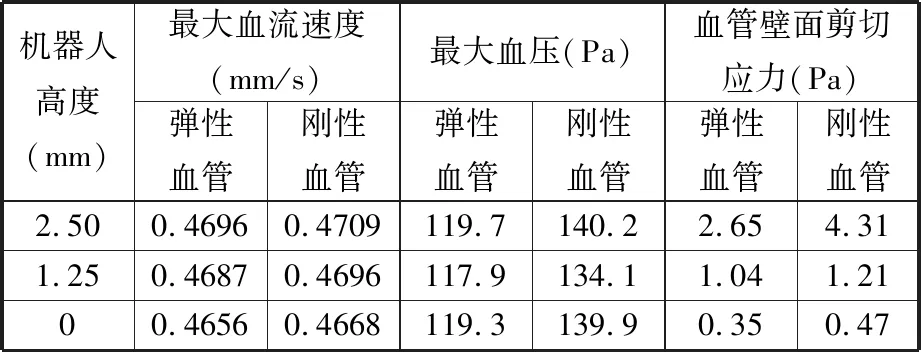
表3 弹性血管模型和刚性血管模型的血流动力学参数(t=0.25 s)

4 介入机器人管内脉动流场实验台

基于磁控机器人管内恒定流场测量系统[18],搭建了介入机器人管内脉动流场测量系统,如图8所示。介入机器人驱动部分主要由六自由度机器手、旋转电机、工作台、外部驱动永磁体、试验管道、螺旋介入机器人等组成。介入机器人系统相关参数与表1相同。实验中,外部永磁体平移速度和转速与数值计算中的数值相同。

(a)全景图

流场测量部分主要由粒子图像测速系统、蠕动泵、压力计、流量计、玻璃水槽、水槽支架和计算机等组成。脉动流由蠕动泵产生,通过流量计和压力计对流体数据进行监控。

结合流量计,对蠕动泵输出流体速度的幅值和脉动频率进行调节,使一个周期的流体速度与图4中的血流入口速度曲线红色部分相近,并将输出流体速度绘制成曲线,如图9所示。

图9 蠕动泵输出流体速度曲线

5 实验结果与分析

图10所示为蠕动泵输出流体速度达到最大值时,机器人在高度2.50 mm处向左运动时周围的流体速度,可以看出,机器人向左运动时,机器人下方存在一个流体高速区,机器人前后方为流体中速区,机器人尾部出现流体低速区。机器人介入后,机器人下方管道变窄,流体压力增大,流速随之增加,形成流体高速区。总体来看,机器人周围流体速度的实验值与计算值大体相似。实验时,外磁体的运动驱动机器人运动,机器人运动的滞后性导致机器人所受磁吸力不沿水平方向,机器人前进时与管壁反复碰撞,因此机器人运动轨迹呈波浪形。数值计算时为了简化计算,假设机器人沿水平方向运动,因此实验测量的管内流体速度没有数值计算结果均匀。

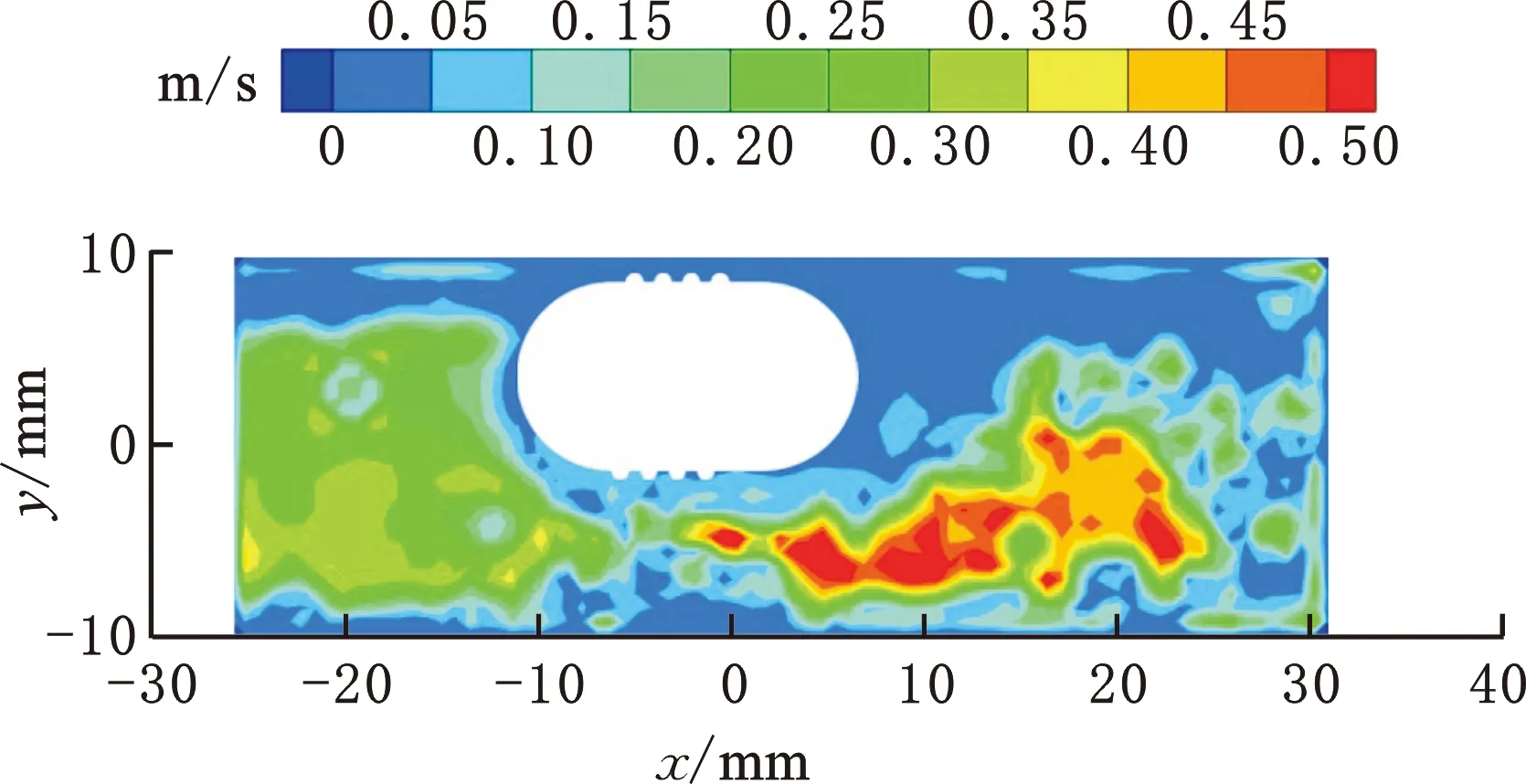
(a)实验测量

为定量比较实验测量和数值计算的结果,建立图11所示的参考坐标系,其中,管道中心轴为X轴,通过机器人中心的垂直线为Y轴,vf为流体速度,vr为机器人速度。

图11 流体速度定量比较的参考坐标系

图12所示为蠕动泵输出流体速度达到最大值时,介入机器人旋进和无介入机器人时的Y轴上管内流体速度的实验值(多次实验测量结果的平均值)和计算值,可以看出,无介入机器人时,对于脉动流入口,从管道底部往上,管内流体速度先增大,再相对平稳,最后减小,数值计算结果变化趋势与实验测量结果基本一致。管内中间段流体区域的数值计算结果与实验测量结果的最大误差约为13.1%。有机器人介入时,从管道底部往上,管内流体速度先快速增大,然后快速减小,机器人位置处的流体速度接近0,数值计算结果与实验测量结果的变化趋势基本一致。机器人和管道之间流体区域的数值计算结果与实验测量的结果最大误差约为19.7%。造成数值计算结果与实验测量结果误差的主要原因是,实验中机器人沿X轴运行时存在一定的上下波动。对比来看,机器人的介入使管内机器人下方流体速度增大。

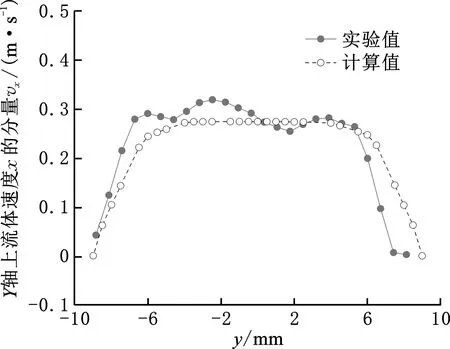
(a)无介入机器人

6 结论

使用双向流固耦合方法获得了介入机器人在弹性血管内运行时的管内流场特性。对比分析了无介入机器人和介入机器人在血管中不同高度时的血流流线和血压的变化差异,讨论了血管壁面剪切应力与血流入口速度的关系。研究发现,机器人的介入对血流速度、血压、血管壁面剪切应力等血流动力学参数有一定的增大作用,但数值均在安全范围以内,不会对血管造成损伤;机器人运行高度的变化对血管壁面剪切应力略有影响;弹性血管模型下的血流速度、血压、血管壁面剪切应力等血流动力学参数均低于刚性血管模型下结果。

搭建了介入机器人管内脉动流场测量系统,在弹性管道中实验测量了介入机器人旋进和无介入机器人的管内机流体速度。结果表明:实验测得的机器人周围流体速度与数值计算结果基本一致,两者误差在20%以内。这对介入机器人运动时管内复杂流场的计算是可以接受的。