基于复合规则和强化学习的混流装配线调度方法

郭具涛 吕佑龙 戴 铮 张 洁 郭 宇

1.上海航天精密机械研究所,上海,2016002.南京航空航天大学机电学院,南京,2100163.东华大学人工智能研究院,上海,201620

0 引言

随着航空航天、汽车等领域的客户化定制需求不断增加[1-2],越来越多的制造企业利用总装阶段的多品种混线生产保障产品的准时交付,并且逐步采用单元式生产模式,利用装配单元的资源配置柔性与物流供应柔性,实现给定生产节拍下的均衡生产。这种方式面临装配单元之间的负载均衡,以及不同产品之间的投产规划等调度难题,需要考虑工人装配能力差异和产品装配时间差异等约束,解决混流装配线的平衡与排序问题,合理安排各装配单元的工人和产品投产序列,提升装配线的生产效率。

针对混流装配线平衡与排序问题,目前的研究方法以启发式规则和智能算法为主[3-4]。RAUF等[5]融合优先级规则与多准则NEH算法,通过对优先级规则进行组合优化,实现了面向多目标集成优化的算法求解。AKYOL等[6]通过设计工人优先级规则和任务优先级规则,提出一种基于多规则的随机搜索算法。DEFERSHA等[7]设计了一种嵌入多阶段线性规划的遗传算法,求解了平衡与排序问题。ZHANG等[8]提出一种多目标遗传算法来集成优化平衡问题与排序问题。智能算法利用全局搜索能力可获得较优解,但需要大量计算时间,难以满足大规模生产的需求。启发式规则能以较短时间获得合理的调度方案,但对调度问题的适应性较差。复合规则对不同启发式规则进行线性加权,能通过参数变化适应不同问题,但参数设置依赖人工经验和试验结果,难以稳定获得较优的调度方案。

随着人工智能技术的发展,强化学习等机器学习方法将调度问题映射为状态-动作转移函数和奖励函数来最大化奖励函数的动作规划过程,获取较优调度方案。贺俊杰等[9]提出一种基于长短期记忆网络与强化学习算法的调度方法来求解最小化加权完工时间的等效并行机在线调度问题。WANG等[10]根据3种启发式规则(底层工序优先、最长加工时间优先和最短加工时间优先),提出一种双层Q-learning算法来求解最小化交付惩罚的装配车间调度问题。TORTORELLI等[11]提出一种基于并行深度强化学习的混流装配线平衡方法,以最小化生产周期。调度问题变化时,强化学习算法需要根据新的状态空间与动作空间重新训练,产生新的大量计算工作。

本文提出基于复合规则和强化学习的混流装配线平衡与排序方法,结合复合规则对不同问题的适应能力与强化学习对具体问题的学习能力,实现混流装配线的生产调度。首先构建混流装配线平衡与排序问题的数学模型,然后分别设计面向混流装配过程的平衡规则库与排序规则库,最后设计近端策略优化(proximal policy optimization, PPO)算法调控复合规则中的参数权重,获取调度方案。

1 混流装配线平衡与排序问题

1.1 问题描述

航天产品的混流装配线具有产品多品种、小批量,批产研制型号混线生产等特点,并且为满足班组操作需求,装配过程具有单元式组织的特点。因此,需要在装配线设计阶段实现各个装配单元之间的负载均衡,保障装配物流的连续性。随着批产订单和研制任务的增加,产能需求出现波动,设计阶段形成的装配单元之间的负载均衡被打破,需要利用装配单元的人员动态配置与不同产品的投产顺序规划,实现混流装配过程的再次平衡,即考虑装配单元容量和工人装配能力等约束条件,合理安排装配单元的工人,并考虑航天产品的最小生产集合(minimum part set,MPS)循环,规划产品的投产顺序,形成混流装配线的平衡与排序解决方案,避免装配单元出现过载和空闲等情况,实现最小化过载时间和最小化空闲时间的优化目标。根据以上生产特点,本文对航天产品混流装配线平衡与排序问题提出以下假设:

(1)工件以固定节拍进行投产;

(2)根据设计阶段的装配任务量,各装配单元具有相同的传送距离;

(3)工人为多能工,能完成多种产品的各项装配任务;

(4)装配单元是封闭的,工人不能在装配单元之间移动;

(5)装配单元内的工人共同完成装配任务;

(6)各装配单元可分配人数固定,工人装配能力存在差异,工人的装配能力影响产品在该单元的装配时间;

(7)过载工作由装配单元内的工人完成;

(8)过载工作对当前装配单元及下一个装配单元产生影响。

1.2 数学模型

混流装配线平衡与排序问题的数学模型如下所示,其中的数学符号如表1所示。

表1 混流装配线平衡与排序问题的数学符号

(1)

s.t.

(2)

(3)

(4)

(5)

p′ik=pikQk∀k

(6)

snk=en(k-1)-c

(7)

enk=snk+p′ik

(8)

uik=max[0,min(snk+p′ik-lk,lk-c)]

(9)

oik=min(0,T-enk)

(10)

式(1)给出了在航天产品混流装配线平衡与排序问题的目标函数——最小化的过载时间和空闲时间。装配单元的工人班组在设计的节距长度内不能完成装配任务时,需要临时延长装配时间以完成过载工作量,这可能会造成其他装配单元的工作延误,并增加潜在的装配质量风险。装配单元的工人班组提前完成装配任务时,由于装配单元的封闭性限制,工人只能等待,这造成了装配能力的浪费,因此需要同时避免装配单元的过载和空闲。式(2)表示由于航天产品的复杂性与尺寸限制,投产序列中的任意位置有且仅有一个待装配产品,即在每个生产节拍中,每个装配单元里仅有一个航天产品被执行装配操作。式(3)表示MPS中的所有产品都被安排到装配线上进行装配,即各个装配单元需要顺次完成一个MPS的产品装配任务。式(4)表示装配线中的所有工人都被安排到装配单元中,以实现工人装配能力的充分利用。式(5)表示根据工人分配结果,计算各个装配单元上的装配时间系数。式(6)表示根据装配时间系数,计算各类型产品在装配单元上的实际装配时间。式(7)、式(8)分别表示投产序列中第n个产品在装配单元k上的装配起始时间和装配结束时间。式(9)、式(10)分别表示投产序列中第n个产品在装配单元k上产生的过载时间和空闲时间。

2 混流装配线平衡与排序方法

针对以上约束条件与优化目标,航天产品混流装配线平衡与排序方法首先构建面向复合规则的平衡规则库与排序规则库,然后设计PPO算法对复合规则中的权值参数进行动态调整,根据复合规则生成平衡方案与排序方案,并计算目标函数(式(1)),对平衡与排序结果进行评价,如图1所示。

图1 基于复合规则和强化学习的混流装配线调度方法

2.1 平衡与排序规则库

2.1.1平衡规则库

在平衡过程中,综合考虑整体装配效率目标和工人装配能力分布[12],对装配单元上的工人配置设计以下规则。

规则b2：选择在装配单元上能力水平最高的工人w*,即满足w*=argmaxqwk。

规则b3：选择与瓶颈装配单元能力水平之差最大的工人w*,即满足w*=argmax(|qwk-qwkb|)。

规则b4：将工人w*分配至装配单元。

2.1.2排序规则库

排序过程中,综合考虑装配单元的操作时间和生产循环的产品需求分布[13],对装配线的投产排序设计以下规则。

规则s4：将产品类型i*投产到装配线。

2.2 近端策略优化算法

如图2所示,在平衡规则库与排序规则库基础上,PPO算法中的平衡智能体与排序智能体分别观察混流装配线的环境状态Sb和Ss,输出复合规则中的规则权重参数,并根据复合规则生成包括平衡调度与排序调度的马尔可夫决策过程,计算平衡与排序阶段的奖励回报函数rb和rs。以历史经验为样本数据,PPO算法设计如下的损失函数:

图2 基于PPO算法的平衡与排序调度过程

(11)

c(Rt(θ),1-ωclip,1+ωclip)=

分别训练平衡智能体与排序智能体。改进网络结构、设计优先经验回放机制,以提高PPO算法的数据利用率。

2.2.1平衡智能体与排序智能体

强化学习算法中的智能体以最大化累计奖励为目标,通过感知环境的状态S、对环境做出的动作A,根据环境的奖励反馈R进行学习[14-15]。为实现以上过程,平衡智能体与排序智能体采用Actor-Critic网络结构,其中,平衡智能体构建Actorb网络和Criticb网络,排序智能体构建Actors网络和Critics网络,利用Actor网络与Critic网络的交互,实现合理的装配单元工人配置与多种产品投产规划。

考虑平衡智能体与排序智能体的动作在装配时间、生产节拍等方面的关联性,在智能体之间设计GRU单元与注意力机制,即在GRU单元中综合考虑Actor网络的输入参数与隐藏状态,通过不断更新隐藏状态,学习平衡过程与排序过程的前后动作关联信息。同时,运用注意力机制加强对平衡过程与排序过程中关键状态特征的学习,提高网络学习的能力。

2.2.2平衡与排序的马尔可夫决策过程

根据混流装配线平衡与排序问题面临的约束条件与优化目标,建立平衡与排序的马尔可夫决策过程(Markovian decision process, MDP)模型,以MDP模型中的状态S、动作A和奖励R描述平衡与排序问题的调度要素。

(1)状态空间。平衡过程中,装配人员的能力水平和装配单元的人员配置是关键状态特征。因此,设计平衡智能体的观测状态空间

(12)

排序过程中,装配单元的产品操作时间和装配任务的开始操作时间是关键状态特征。因此,设计排序智能体的观测状态空间

Ss=(p′ik,d′i,snk,lk,T)

(13)

(2)动作空间。根据所设计的平衡规则库,得到混流装配线平衡阶段复合规则的评价值:

Hbi=ωb1hb1+ωb2hb2+ωb3hb3+ωb4hb4

(14)

式中,ωb1～ωb4为平衡智能体根据当前状态输出的规则权重;hb1～hb4为平衡规则b1到b4的评价值。

根据设计的排序规则库,得到混流装配线排序阶段复合规则的评价值:

Hsi=ωs1hs1+ωs2hs2+ωs3hs3+ωs4hs4

(15)

式中,ωs1～ωs4为排序智能体根据当前状态输出的规则权重;hs1～hs4为排序规则b1到b4的评价值。

(3)奖励函数。根据Actor-Critic算法框架,需要根据平衡与排序方案的评价函数f,对平衡智能体与排序智能体进行训练。考虑到平衡与排序问题的复杂性与规模性,以上训练过程会使训练过程迭代变慢,降低算法收敛速度,因此需要重新设计奖励函数。平衡过程中,将混流装配线的过载时间和空闲时间平均分配到每个动作回合,得到平衡阶段的奖励回报函数:

(16)

式中,tb为平衡过程的总步数;C为生产节拍常数。

排序过程中,根据每个排序动作产生的装配单元过载时间和空闲时间,定义排序阶段的奖励回报函数:

(17)

2.2.3优先经验回放机制

传统PPO算法在学习过程中进行历史样本的随机采样,在面临优化问题时的学习能力有限[16],因此提出一种优先经验回放机制,根据平衡与排序问题的目标函数值fi设置经验样本i被学习的概率即调度经验样本τ的采样概率

(18)

式中,i为经验库中调度经验样本τ的编号;T为经验库中所包含的调度经验样本总数。

通过权重保留较优经验进行采样,提高PPO算法的学习效率。

2.2.4算法训练流程

马尔可夫决策过程中,平衡智能体、排序智能体分别观察混流装配线平衡与排序过程中的状态空间Sb和Ss,Actorb网络和Actors网络输出复合规则的权重向量,通过集成平衡规则库与排序规则库,生成平衡调度方案与排序调度方案,得到式(16)、式(17)所示的奖励函数。将平衡智能体、排序智能体与混流装配线环境互动过程中的调度经验储存在经验库中,当经验库达到最大容量时,基于优先经验回放机制对历史经验进行采样,更新Actor与Critic中的网络参数分布,并通过经验回放的不断迭代,调控优化智能体的动作策略。以上过程中的算法步骤如下:

(1)初始化平衡智能体与排序智能体的Actor-Critic网络参数θb、θs、ψb、ψs,设置智能体中的迭代最大回合数emax、经验库容量z、经验库最大容量zmax;

(2)初始化航天产品平衡与排序问题调度环境,设置平衡智能体的工人配置步数tb=0与排序智能体的产品投产步数ts=0;

(3)根据平衡规则库,平衡智能体观察环境状态Sbt,根据策略πθb(abt|Sbt)输出复合规则权重向量,分配工人w*至装配单元,更新环境状态Sbt;

(5)根据排序规则库,排序智能体观察环境状态Sst,根据策略πθs(ast|Sst)输出排序规则权重向量,选择产品类型i*进行投产,更新环境状态Sst,反馈奖励函数值rst;

(8)更新平衡动作策略网络πθb(abt|Sbt),排序动作策略网络πθs(ast|Sst);更新平衡评价网络vψb(abt,Sbt),排序评价网络vψs(ast,Sst);更新网络参数θb、θs、ψb、ψs;

(9)若迭代循环次数达到最大回合数emax,训练结束,否则重复步骤(2)～步骤(8)。

3 算例验证

考虑PPO算法参数对复合规则学习过程的影响,结合多品种小批量生产与装配单元工人配置柔性等特点,首先利用随机算例进行混流装配线平衡与排序方法中的算法参数实验,然后根据文献[17-18]设计的标准化算例进行不同平衡与排序方法的对比实验。以上实验采用Intel i7-10875H CPU,内存16G,Windows11的计算机环境,对比方法包括PPO+单一规则、复合规则和遗传算法等调度方法。对比算法的具体说明如下:

(1)PPO+单一规则。使用PPO算法训练强化学习智能体,根据调度状态选取某条规则作为调度动作来选择备选工人或产品。

(2)复合规则。使用正交试验方法设计复合规则的权重,根据复合规则选择备选的工人或产品。

(3)遗传算法。采用十进制编码分别构建平衡过程与排序过程的染色体,平衡过程中的染色体进行循环交叉,排序过程中的染色体进行优先交叉。交叉变异过程采用两点交换法,通过三元锦标赛法和精英保留策略进行染色体筛选,最后根据染色体编码情况生成调度方案。

在算法参数实验中,以面向9种产品类型、包含10个装配单元的混流装配线为研究对象,在单元长度100 s、投产节拍为120 s的情况下,根据单元工人容量U[2,3]、产品数量U[4,7]、工人装配能力U[0.8,1.2]、产品装配时间U[80 s, 130 s]的分布情况,随机生成3个算例。通过正交试验分析以上算例中的PPO算法参数水平,得到PPO算法参数:Actorb的学习率RA,b=5×10-5,Criticb的学习率RC,b=5×10-5;Actorb网络结构参数为(256,128,128);Criticb网络结构参数为(256,128,128);Actors的学习率RA,s=5×10-5;Criticb的学习率RA,s=5×10-5;Actors网络结构参数为(256,128,128);Critics网络结构参数为(256, 128, 128)。

PPO+单一规则方法与表7所列算法参数设置相同,复合规则方法的权重设置基于三因素五水平的正交试验,平衡规则的权重wb1=0.25,wb2=0.625,wb3=0.125,排序规则的权重ws1=0.3,ws2=0.5,ws3=0.2;遗传算法初始种群规模100、交叉率0.8、变异率0.05、迭代次数200。在上述算法参数设置基础上,根据文献[17-18]中的生产循环、装配单元和工人设置,生成标准化算例,采用本文方法和对比方法进行求解,得到混流装配线调度问题的目标函数值f与方法运算时间即CPU time,结果分别如表2、表3所示。

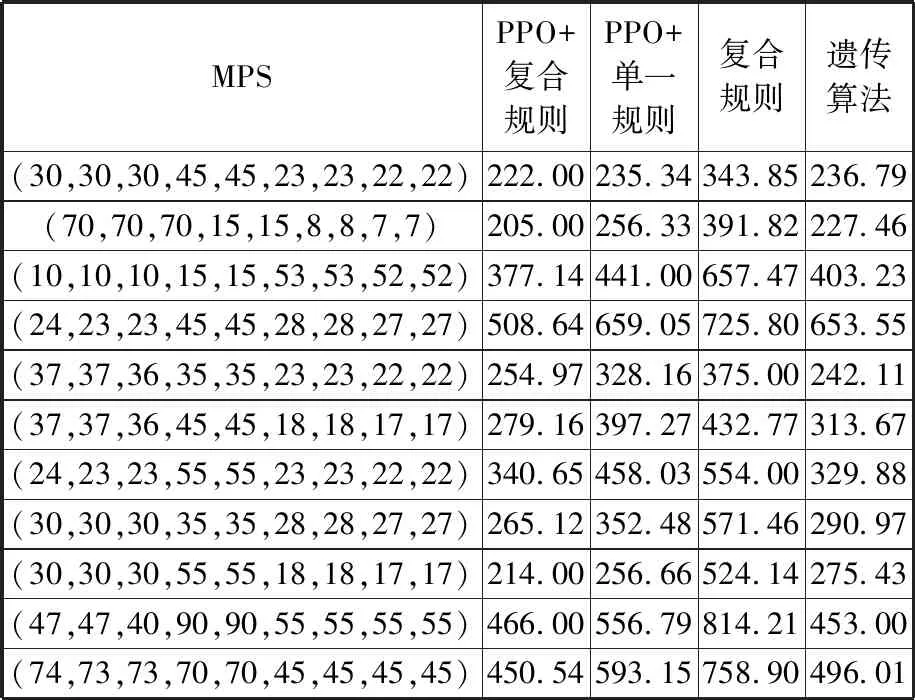
表2 不同方法的目标函数值结果

表3 不同方法的运算时间

如表2、表3所示,对于工人数量、装配单元数量、产品种类和产品数量共同决定的混流装配线平衡与排序问题的大规模解空间,PPO+复合规则方法利用平衡智能体与排序智能体,将多个启发式规则组合成复合规则,具备较好全局优化能力,并根据调度问题的目标函数设计了奖励回报函数,建立了基于PPO算法的学习过程,不断对复合规则中的权值进行动态调控,具备较好的局部适应能力,因此获得了平衡与排序问题的更优解,并缩短了计算时间。在大规模解空间中,PPO+单一规则方法容易在初始化阶段就陷入部分区域,使学习过程倾向于持续选择某个规则,导致算法过早陷入局部最优。该方法虽然在较短时间内获得了可行方案,但难以进一步生成更优方案。复合规则采用正交试验对启发式规则权重进行有限调整,虽然缩短了参数寻优的计算时间,但对大规模问题的优化十分有限,很难生成符合调度方案优化需求的复合规则,仅能获得次优解或可行解。遗传算法需要扩大种群规模、增加迭代次数来满足大规模解空间的全局搜索需求,但计算时间的大幅度延长,且增大后的种群规模难以形成有效的局部搜索能力,因此对大部分MPS难以获得近优求解效果。

4 结论

针对多品种小批量、单元制造的航天产品混流装配线平衡与排序问题,结合复合规则对不同调度问题的适应性与强化学习对调度问题的策略学习能力,提出一种基于复合规则和强化学习的混流装配线平衡与排序方法。在分析问题特点与数学模型的基础上,分别设计了平衡规则库与排序规则库,提出的强化学习PPO算法对规则组合下的复合规则权重参数进行调控优化,根据复合规则生成混流装配线平衡与排序方案,最小化装配单元的过载时间和空闲时间。所提方法与PPO+单一规则、复合规则和遗传算法的求解效果对比验证了所提方法的有效性。在此基础上,后续研究将关注混流装配线调度问题特点与PPO算法中复合规则权重分布的可解释性映射关系,进一步挖掘混流装配线平衡与排序方法中存在的调度机理。