基于点云曲面的定角度自动铺丝路径规划

2023-11-17姜世阔王小平

中国机械工程 2023年21期

姜世阔王小平汪凯金将

南京航空航天大学机电学院,南京,210016

0 引言

相比于传统材料,碳纤维复合材料具有小质量、高强度、高模量、设计制造一体化等优点,已成为航空航天制造工程的基础材料[1]。自动纤维铺丝(automatic fiber placement,AFP)是一种高效的复合材料自动化制造技术,具有曲面适应性强、铺放自由度大、成品率高等优点,因此,自动铺丝技术已成为复合材料自动制造技术的研究热点。自动铺丝路径规划作为自动铺丝技术的研究重点,已取得一系列成果。

PARNAS等[2]以双三次Bezier曲面表示芯模曲面,将Bezier曲线的控制点作为设计变量来生成铺丝路径。SCHUELER等[3]以样条线拼接技术构造初始路径。SHIRINZADEH等[4]提出了以平面与芯模曲面相交来构造初始路径的截平面法。BLOM等[5]以参数曲面的形式提出了定曲率、定角度曲线和测地线3种圆锥类构件的铺丝路径算法。WANG等[6]引入微分几何的原理,使用数学方程表示初始路径和偏移路径,将纤维路径规划问题改变为求解一阶常微分方程的初始值问题,该方法计算简单且精度较高。卢敏等[7]提出一种基于投影法的铺丝路径规划方法,即将铺丝路径主应力分布关键点偏移到曲面一端拟合成曲线后,再将拟合曲线投影到原曲面作为初始路径。孟书云等[8]提出一种可自动生成铺丝路径的经线包络法,根据曲面几何特征、自动铺丝纤维数量等相关工艺参数,自适应生成定角度的铺丝路径。年春波[9]使用Hermite曲线描述纤维的铺放路径,并使用开边柱面模型验证了算法的有效性。LONG等[10]提出一种基于微分几何的精确滚子路径规划方法,以减少两条丝束之间的间隙和重叠,提高铺丝质量。XU等[11]采用映射法在网格曲面规划铺丝路径,即先将多面体表面展平为平面网格,然后在平面网格规划路径,最后将规划的路径映射回初始网格。该方法误差过大,仅适用于可展曲面等简单曲面。李俊斐等[12]将传统参数曲面路径规划中的定角度法引入网格曲面,但没有给出一套完整的铺放方法。朱延娟等[13]研究了在三角网格曲面上生成测地线的算法,并以此为基础提出一套自动铺带轨迹路径的规划方法。PEI等[14]提出基于模型几何信息与承载信息局部优化的铺丝路径规划方法,某后机身模具的实际铺放证明了该算法的有效性。王小平等[15]提出的改进网格定角度初始路径规划算法避免了传统参数化求解过程的无解和多解。冉庆波等[16]提出针对含孔网格曲面的自动铺丝路径规划算法。周宇[17]提出了一套完整的三角网格曲面自动铺丝路径规划算法,该方法适用于曲率变化较大的复杂曲面或拼接曲面。

目前,铺丝路径规划的研究主要集中在参数曲面与网格曲面。在参数曲面上进行路径规划需借助曲面的参数表达式,但以参数方程表达复杂曲面是十分困难的。虽然网格模型可以表达复杂的曲面,但对于某些无法获得数字模型的产品(如竞争对手的产品),产品开发人员往往面对的是实物。伴随着三维扫描设备的发展,以点表示的点云模型应运而生。点云模型简单的数据结构可以灵活表示复杂的实物模型,已成为逆向工程领域的研究热点[18]。工程上,扫描得到的点云数据通常先转化为三角网格或曲面,再进行后续的加工。重建曲面过程繁琐,重构的曲面与原曲面之间存在一定误差,且产品制造过程中往往需要反复修改点云数据,不利于产品的后续开发。因此,研究直接在点云曲面上生成铺丝路径的规划算法,不仅缩短了产品制造的时间,为铺丝产品的设计与优化提供技术支持,而且对促进我国复合材料自动铺丝技术的发展具有重大意义。

目前,针对点云曲面的铺丝路径规划算法还鲜有报导,因此本文以点云曲面为研究对象,提出基于点云模型的铺丝路径规划算法。根据截平面法原理和点云曲面的离散特征,提出将初始路径离散成一组点并投影到点云曲面的直接投影法。针对自动铺丝工艺的特点,以点云投影算法改进点云切片法,提出点云投影切片法。使用三次B样条插值法对得到的投影点进行插值,生成初始路径,并使用具体算例验证了该方法的有效性。在点云曲面上以弦长代替弧长,实现了初始路径的平行等距偏移,并针对该方法的不足提出弦长细化投影法。通过CATIA逆向工程模块实现了算法的可视化验证,建立了三维建模软件与所提路径规划算法之间的联系。

1 初始路径

采用自动铺丝制造的飞机零件一般以准各向同性为铺放目标,大多采用0°、±45°、90°等定角度轨迹循环铺放成形。初始铺放路径是在综合考虑构件的曲面特征、加工工艺等条件下,预先规划和生成的,其余路径以初始路径为基准进行的等距偏移[19]。将参考传统参数曲面[2-8]和网格曲面[8-16]常见的路径生成方法——截平面法引入点云曲面。

1.1 法向量

点云模型一般仅包含数据点的位置信息,不包含法向量等信息,而法向量对后续工作的进行至关重要,因此,先计算各点的法向量。假设点云曲面S={P1,P2,…,PN},点云中的数据点Pi=(xi,yi,zi)∈R3,i=1,2,…,N。三维点云中任意点的法向量一般采用主元分析法(principal component analysis,PCA)[20]计算。对点云中的任一点P,获取与其最相近的k个相邻点,构造协方差矩阵

(1)

对协方差矩阵进行特征分解,将最小特征值对应的特征向量作为P点的法向量。PCA算法的鲁棒性较差,因此使用高斯加权的PCA算法来获得更精确的法向量:

(2)

式中,σ为常数。

1.2 直接投影法

截平面法是自动铺丝路径规划中生成初始路径的经典算法,其原理是创建平面与曲面相交,以交线为铺丝路径轨迹。根据截平面法的原理,可以将其视为平面上的一条直线或曲线沿给定方向投影到构件表面生成初始路径,如图1所示。投影可以看成计算投影线与曲面的交点,文献[7-8,11]详细阐述了直线或曲线投影到参数曲面或网格曲面的方法。点云曲面没有固定的表达式或拓扑结构,只有离散位置信息。将直线或曲线投影到曲面重建点云表面不仅耗时,而且重建的精度也不高。一种行之有效的方法就是先将直线离散成一系列点,再将离散点投影到点云表面,最后对投影点进行插值处理,生成实际的初始路径。

图1 截平面原理示意图

移动最小二乘(moving least squares,MLS)是点云模型中曲面拟合的重要方法[21],包括生成局部参考平面和曲面多项式拟合两个步骤。设p为待投影点,n为投影向量构造投影线。查找点云中与投影线距离小于规定搜索半径r的所有点,并将其组成投影点集S1={Pj|Pj∈S,j=1,2,…,m},如果m<3,则适量扩大搜索半径。点Pi与投影射线的距离

(3)

设p在局部参考平面上的投影点为x。该点法向量nx由S1各点法向量加权组合近似得到:

(4)

(5)

式中,θ(x,Pj)为权函数,本文取高斯函数;d(x,Pj)为点Pj到投影射线的距离;h为投影域的大小。

设过x点以nx为法向量的参考平面为H,其表达式为

(6)

(7)

式中,w(Pj,x)为在点k邻域内光滑、单调递减的正值函数,本文取为高斯函数。

式(6)衡量测量参考平面与点云的拟合质量,取得最小值时,可以获得最佳局部参考平面。通过上述计算得到局部参考平面H之后,定义平面H为XY面,以x为原点,以垂直局部参考平面的方向为Z向,构建局部坐标系。局部坐标系下,设qj为点Pj在XY面上的投影点,fj为点Pj与面XY的距离,即fj=nx·(Pj-x),如图2所示。然后构造如下目标函数:

图2 点云投影示意图

(8)

式中,(xi,yi)是点Pj∈S1在XY面上的坐标;g(xi,yi)表示移动最小二乘意义下局部拟合曲面的双变量多项式。

通过最小化式(8)即可得到移动最小二乘意义下局部拟合曲面的双变量多项式。p在局部拟合曲面上的投影点p*可以通过双变量多项式在局部直角坐标系原点处的坐标求得[22],即

p*=x+g(0,0)n

(9)

为保证算法的计算精度,参考XU等[23]提出的方法对上述算法加以改进。引入权重的阈值:

(10)

式中,wmean、wmax分别权重的平均值和最大值;l为迭代次数。

如果S1中某点的权重大于wlim,则保留;否则,将其从S1中去除。将获得的点集作为新的投影点集,将当前得到的投影点作为新的待投影点,再次进行投影,直到前后两次投影点的距离小于给定的阈值ε(本文取ε=0.01),或最大投影迭代次数lmax(本文取lmax=10)终止迭代。

在选择投影点集S1时,本文以距离投影线较近的点作为投影点集,但这样可能将一些距投影点位置较远的点选择进来。例如,将点以法向投影到圆柱面上半面时,根据数据点到投影线距离选择投影点集会将圆柱面下半面的点也选择进来。为解决这个问题,参考文献[22]对S1的选取方法加以改进:

(1)计算S1的中心,通过中心点创建一个垂直于投影光线的平面。该平面将S1点集分为点集S11和S12。

(2)计算S11和S12的中心点与待投影点p的距离,将中心点与待投影点距离较短的点集选为候选点集。

(3)重复步骤(2),直到输出的点集变为连续的点集。此时输出最终的投影点集。

1.3 投影切片法

使用直接投影法生成初始路径的方法需要提前设计一条初始路径,然后,将该路径离散化,并投影到点云曲面上。为实现铺丝路径规划的自动化,在参考点云数控加工[24-26]的相关工作后,本文提出点云投影切片法来生成初始路径。

点云切片法是一种基于点云模型特点的“截平面法”,先通过一组平行平面分割点云模型来确定截平面上的数据点,再利用这些数据点组成截面线,具体原理如图3所示。图3中,E为截平面,为求取平面与点云曲面的交线,在E的两侧以δ/2的距离生成平面E1、E2,其中,δ为切片厚度,与点云密度相关,一般选为密度大小的1～4倍[25]。

图3 点云切片法原理示意图

使用点云切片法求取交线的方法通常是投影法和求交法。投影法先将切片区域内的点云投影到截平面,再通过拟合投影点生成交线。该方法计算简单,但易产生冗余数据,误差较大。求交法先搜寻平面两侧的最近点,再以最近点连线与平面的交点来近似表达交线。该方法不受模型表面形状的限制,但计算过程复杂、繁琐,且截面线的精度受点云密度影响较大。定方向铺丝路径一般涉及多个角度,传统的切片法难以保证截面线的精度,因此,本文提出一种改进的点云投影切片法,具体步骤如下:

(1)计算点云质心

(11)

并以点云质心为原点构建空间坐标系。

(2)以垂直初始路径方向为截平面法方向,过点云质心创建截平面E。以平行于截平面且与截平面距离δ/2生成平面E1、E2,得到位于切片区域内的数据点。

(3)先将步骤(2)得到的数据点绕Z轴旋转,使截平面与OXZ平面重合,再将旋转后的切片数据点向截平面E投影,并将投影点集记为T。

(4)计算T中每一个点与X轴正向夹角。将夹角极小点和极大点记为始末点,并加入点集I。根据与X轴正向夹角,以固定步长将投影点集T划分为多个扇形区域,计算各扇形区域中的数据点与质心O的距离,并将距离最大者加入点集I。

(5)将点集I中的数据点以指向质心方向为投影方向,按照1.2节的方法投影到点云曲面,并记录投影点坐标。将投影点以步骤(2)的反方向绕Z轴旋转回点云原坐标系。最后将投影点依次连接,得到截平面与点云模型的交线。

1.4 B样条插值

以上算法得到的均是初始路径的投影点,将这些投影点依次连接就得到了初始路径。航空航天领域的产品往往要满足空气动力学或工艺的要求。因此本文引进三次B样条插值对投影点进行插值处理,将插值后的曲线作为初始路径。将上文得到的投影点称为待插值点qi(i=1,2,…,n)。k次B样条曲线的定义如下:

(12)

式中,di为控制顶点;Ni,k(u)为B样条的基函数。

三次B样条曲线的基函数为

(13)

则第i段三次B样条曲线的表达式为

(14)

工程实践中,三次均匀B样条插值可以满足自动铺丝的要求。使用三次B样条曲线对插值点进行插值处理,需要先从已知点反求出相应的控制点,再对控制点进行拟合。由每段B样条曲线端点处的性质,建立插值点与控制点之间的关系:

di+4di+1+di+2=6qi

(15)

式(15)为反求控制点的方程组。根据式(15)可知,方程组中有n个方程,而未知控制点为n+2个,因此需要补充2个条件。为保证整条曲线经过首末两点,补充边界条件:d0=d1,dn+1=dn,最终将式(16)写成矩阵形式:

(16)

使用追赶法求解式(16),得到三次B样条插值曲线上的控制点,进而得到插值曲线。

初始路径的数据点分布不均匀时,采用均匀参数化B样条插值将导致插值曲线打圈自交。因此,在使用直接投影法生成初始路径时,需将投影直线或投影曲线以合适的步长均匀离散化为待投影点,待投影点在曲面上的投影点也将在一定程度上保持均匀分布。对投影切片法而言,待投影点是在固定步长均匀划分的区间内获得的,投影后的投影点近似均匀分布。

1.5 算法验证

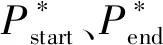
(a)抛物面 (b)可展曲面

(2)验证投影切片法。图5a、图5b所示为投影切片法在圆柱面点云曲面上生成的45°初始路径,其中,红线为插值后的初始路径,蓝线为参数曲面求解得到的初始路径。图5c、图5d所示为切片投影。

(a)均匀圆柱面点云 (b)散乱圆柱面点云

由图4、图5可以看出,直接投影法与投影切片法均可生成一条与实际路线相近且较为平滑的初始路径,投影切片法对非均匀点云曲面仍然有效。

2 路径密化与边界处理

生成初始路径后,其余的路径以之为参考进行密化。为避免铺丝时的路径发生干涉,以及丝束间产生间隙和重叠,一般采用在曲面上平行等距偏移的方法对初始路径进行密化,实现路径的完整覆盖[28]。文献[6]提出一种将初始路径的等距密化问题转换为求解参数域中一阶常微分方程初值问题的方法。ZHANG等[29]将初始路径上的点视为光源,通过控制光的传播时间间隔进行初始路径的平行等距传播,实现在网格曲面上铺丝路径的密化,但这两种方法不适用于点云曲面。对于表面平坦的构件,曲面相邻两点之间的距离与直线连线后的弧长非常接近,因此求解偏移路径时可以采用弦长代替弧长的方法。

2.1 偏移算法

为求取偏移方向,首先采用1.1节的方法计算投影点各点处的法向量,使用第1.4节的三次B样条插值方法生成初始路径。对B样条函数求取一阶导来获得各投影点的切向量。三次B样条的表达式求导之后的矩阵表达式为

(17)

使用1.3节方法得到控制点列,重新拟合B样条基函数求导后的表达式即可得到每个投影点处的切向量。

2.2 路径偏移

对于表面平坦、光滑的构件,曲面上相邻两点之间的弧长与直接连线后的弦长非常接近,因此可以采用弦长代替弧长的方法近似求取等距偏移点。近似偏移点与实际偏移点的误差在允许的范围之内即满足铺放工艺的要求。

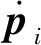
图6 路径偏移原理图

(18)

根据微分几何的相关知识可以得知,向量D′与初始路径垂直,与曲面相切,模长与D相等,符合平行等距的计算要求。在求得D′之后,采用1.2节的方法将D′沿法向投影至曲面,求得偏移点在曲面上的投影点Q。设q点至Q点处的局部曲率半径或平均曲率半径为R,弧长、转角分别为L和θ,如图7所示。

图7 弦长代替弧长的误差分析图

根据图7得tanθ=|D′|/R,而L=Rθ,则误差

e=L-|D′|=Rarctan(|D′|/R)-|D′|

(19)

由式(19)可以看出,该方法仅适合曲率较小的构件生成的偏移路径。对于曲率较大的构件,使用该方法偏移后的路径会产生较大的偏差。因此,改进该方法,提出弦长投影细分法,具体步骤如下:

(1)采用弦长替代弧长的方法生成投影弦,按照固定步长在弦上取n个点,以这些点的法向为投影方向,按照1.2节的方法将这些点投影到点云上。

(2)计算相邻两个点之间的弦长,并按照顺序累加弦长,直到长度恰好超过规定的弧长,记录此时的区间。

(3)采用二分法细分步骤(2)所得区间,直到累计弦长与弧长之间的误差收敛到规定的误差阈值(本文取0.01)。

求得偏移点之后,采用1.4节的三次B样条插值法插值得到偏移曲线。其余的偏移曲线以上一次求得的偏移曲线为基准,使用2.2节的方法求得,直到偏移曲线到达曲面边界。

2.3 边界延伸

路径偏移密化的过程中,构件的几何特征会导致一些不可避免的问题:①生成的路径超出曲面的边界。这个问题的解决方法通常是舍去超出边界的部分,如图8a所示。②生成的路径不与曲面边界相交,如图8b所示,左上角的一些曲线无法到达曲面的边界。针对这种情况,本文采取的方式是选取未达到曲面边界路径的末端点,求取路径末端点处的切方向,并以该点切方向为延伸方向做一条射线。采用1.2节的方法将射线离散后投影到点云曲面上,直到投影点超出边界或与边界相交。最后将投影点使用B样条插值的方法进行拟合,得到满铺路径。

(a)舍去多余边界 (b)边界延伸

3 仿真结果

3.1 直接投影法的算法验证

在开曲面构件中对基于直接投影法的铺丝路径规划进行可视化验证,结果如图9所示,其中,蓝色曲线为直接投影法生成的初始路径,红色曲线为以初始路径为基准等距偏移的满铺路径。直接投影算法在开曲面构件上可以生成与曲面贴合良好的铺丝路径。

(a)0°铺放路径 (b)90°铺放路径

3.2 投影切片法的算法验证

雷达罩、机身尾段等飞机零部件都是典型的锥形闭曲面构件,也是由自动铺丝成型工艺制造的典型构件。A380飞机的尾段蒙皮是采用自动铺丝技术制造的[30]。为验证本文算法的工程应用价值,基采用CATIA对某机型后机身段锥壳构件进行数字化建模,并将其转换成点云模型。采用本文算法对模型进行路径规划,最后通过逆向工程模块对本文算法规划的路径进行可视化验证。图10所示为后机身CATIA三维模型及其点云模型。图11所示为本文算法生成的0°、90°、±45°的铺丝路径,其中,0°铺丝路径以芯模轴线为参考线生成投影;将由投影切片法生成的路径点数据批量导入CATIA,在CATIA中拟合数据点来对路径进行可视化,最终效果如图12所示。