化可分离凸规划为对偶规划显式模型的普适解法研究比较1)

彭细荣 隋允康

* (湖南城市学院土木工程学院,湖南益阳 413000)

† (北京工业大学材料与制造学部,北京 100022)

引言

Fleury 首先将非线性对偶规划引到结构优化领域,进行建立模型和求解算法的研究[1-3].钱令希团队用对偶序列二次规划算法求解结构优化问题[4].结构优化中经典的优化求解算法如CONLIN (convex linearization method)[5]是基于对偶算法.Svanberg[6]提出的移动渐近线法(MMA)也是基于对偶算法.Beekers 等[7]和Hoppe 等[8]均是较早研究了利用原-对偶算法解决结构优化问题.隋允康等[9-10]结合累积迭代信息策略,研究了对偶算法在结构优化中的方法和应用.吴京等[11]和金鹏等[12]用对偶规划研究了钢管混凝土拱结构优化设计问题.Xuan 等[13]在优化层应用对偶内点法的线性规划和在分析层应用二次规划法求解非光滑结构优化问题.Etman 等[14]研究了利用对偶理论的近似对角二次规划法.Cronje 等[15]探讨了序列对偶近似规划中约束的等效性.Liang等[16]通过序列整数规划和典范对偶理论求解结构拓扑优化问题.

多数结构拓扑优化方法对应的模型归结为非线性规划,如均匀化方法[17],变密度方法[18]、ICM(独立连续映射)方法[19-21]、水平集方法[22-23]、拓扑导数法[24-25]、MMC(可移动变形组件)方法[26]、CBS(close B-splines)方法[27]等,可以采用基于非线性规划理论的各种求解算法.如果采用数学规划对偶理论,借助原-对偶变量的显式关系,将大规模的原问题转化为小规模的对偶问题求解,可以大幅度地提高算法的效率[19-21].然而,对偶目标函数却是一个含参数的极小化问题,难以求解出对偶目标函数的显式表达式,只得转而求其1 阶导数和2 阶导数,构造二次规划逼近对偶规划,迭代求解,最后由对偶问题最大解求出原问题的最小解.

隋允康等[28]从优化所建立的数学规划模型的特点出发,针对一大类广泛遇见的变量可分离的凸规划问题,突破了只是停留在对偶目标二阶近似的定势,推导得出了显式的对偶目标函数.在这一研究的基础上,提出了便捷求解的对偶规划显式模型(dual programming-explicit model,DP-EM)方法,并将其应用于ICM 方法[19-21]求解连续体结构拓扑优化问题,将DP-EM 方法与基于DSQP 算法及MMA 算法[6]的方法进行计算效率对比,结果显示DP-EM 方法具有更高的求解效率.

本文的工作旨在进一步提升DP-EM 方法的境界,隋允康等[28]提出的DP-EM 方法仅解决了优化模型中约束和目标函数的每一项均为幂函数形式的情况(对应于本文所列举的情况3: 幂函数形式的解法),而本文把常见的一类变量可分离的凸规划模型抽象为普适的可分离规划列式,在需要满足的一些条件下,转换为DP-EM 解法.相关工作有4 个具体的成果: (1)对偶变量迭代逼近法;(2)指数函数形式的解法;(3)幂函数形式的解法;(4)基于变换的精确解法.这一工作有深度与广度两方面的意义: (1)深度方面,加深了结构优化对偶解法的研究,相关的结论在结构拓扑优化里得到了验证;(2)广度方面,对数学规划对偶理论的发展做出了新贡献.预期今后无论在数学规划寻优算法和结构拓扑优化的求解中,都将会有进一步的应用.

1 普适的可分离凸规划转换为DP-EM 解法

可分离规划通常可以表达为

其中fi和gji为任意的单变量函数,即目标函数与约束条件属于可分离函数形式.

式(1)的拉格朗日函数为

其中 λj(j=1,2,···,M)为拉格朗日乘子.

原问题(1)的对偶问题为

式(4)的库恩-塔克条件为

式(5)表明存在如下的函数关系

式(6)表达了抽象的原-对偶设计变量关系,当对偶规划的最优解求出来之后,需根据具体的原-对偶设计变量关系式(5)由对偶规划的最优解求出来对应的原规划最优解.可以按如下两步求解式(5).

先得到如下非线性方程的解

由式(7)的解得到

为了给推导对偶规划的海赛阵做准备,先将式(6)代入式(5)得

对偶规划有如下结论[2-3]

由式(10)可列出对偶目标函数的梯度向量,而其海赛阵的元素则可在式(10)继续求偏导数给出

由式(12)得

式(13)是i∈Ia的结果;若i∉Ia,则有

于是,若i∉Ia时,将式(13)和式(15)代入式(11),就得到了

有了式(10)和式(16),就可以构造对偶规划的近似2 阶显式

其中 λ(v)取上一次的最优解 λ∗作为本次的初始点,以便构造第v次的对偶二次规划模型.

当第v次寻优收敛后,需要代入式(6)求出对应的原变量最优解.不过式(6)只是理论上的表达,具体将第v+1 次的最优解 λ(v+1)代入式(7)求出xs,然后代入式(8)得到第 µ +1 次的原变量x(µ+1),这里的µ与v不同,它表示结构重分析的指标.经过在x(µ+1)的结构重分析之后,重新构造新的对偶规划式(17),其中梯度向量和海赛阵分别按式(10)和式(16)构造,此时的式(17)中的v清零,取 λ(0)=λ(v+1),这里的 λ(v+1)是前一次的最优解,开始新一轮的对偶规划寻优,式(3)是一个迭代的寻优序列,直到得到新一轮的最优解为止.然后,再求出新的原变量.

值得探讨一下式(7)的算法实现.在求解式(7)时,于具体的 λ 值,除了可按变量xi非线性方程式求解,常常会遇到显式解,更为方便.

由于式(16)中含有 λj(j=1,2,···,M),因而需对此进行处理,使对偶二阶导数不显含对偶变量.下面给出4 种处理方法,分别是: (1)对偶变量迭代逼近法;(2)指数函数形式的解法;(3)幂函数形式的解法;(4)基于变换的精确解法.

1.1 对偶变量迭代逼近法

在迭代寻优过程中,取式(13)中的fk(λj)=(ti)β为上一次的变量,于是海赛阵中就不显含本次的对偶变量了.

至于由对偶规划的最优解按式(7)和式(8)求出对应的原变量,一般要求解N个变量xi各自的非线性方程解,有时存在原-对偶变量之间的显函数关系可以利用,从而勿需求解非线性方程.

1.2 指数函数形式的解法

若约束函数存在下述形式

其中aji和bi为实数值.

将式(18)代入式(16)得

为了将式(19)中含 λj(j=1,···,M)的项消除,现将式(18)代入到式(5),得

将式(20)代入式(19)得

为了求出原-对偶变量的函数关系,假定有

将式(22)代入到式(20)得

若上式右边大于0 能够保证,则得到原-对偶变量的如下显式关系,避免了非线性方程的求解

1.3 幂函数形式的解法

若约束函数存在下述形式

其中aji和bi为实数值.

同上一情况类似,可以推导出

为了求出原-对偶变量的函数关系,假定有

将式(25)和式(27)代入式(5),得到原-对偶变量的如下显式关系

上式开方时必须注意实根的存在.

1.4 基于变换的精确解法

第2 和第3 种处理针对两种函数形式的情况,能否给出约束函数更一般情况的处理？本文就如下情况予以回答.

若

满足凸函数条件,则将式(29)代入式(1)得

引入变换及其逆变换

代入式(30)得

仿前面的推导,得如下结果

其中表达原-对偶变量关系的式(36)并不需要解非线性方程,记

由式(37)解得后,可得规划式(30)的解

以上的4 种处理尽量不采用第1 种,原因是多了一个对 λ 的迭代过程.当分离的每一项函数形式为指数函数或幂函数时分别按第2 种和第3 种处理,一般情况下可采用第4 种处理.

2 算例

本研究团队以往用对偶规划求解结构优化问题时,多遇到幂函数的情况,故多按第3 种情况进行了处理,当时的推导均为个案进行,现以算例2 至算例5 中4 类不同结构拓扑优化问题为例,按本文的结果进行了验证.算例1 为特别设计的简单数学算例,以比较按第1 种情况和第4 种情况处理的效率,其它算例均是按第3 种情况处理.

2.1 算例1: 普适处理的效果比较

取

计算如下可分离非线性优化问题

取初值 (x1,x2)=(0.01,0.01),按第1 种情况处理,迭代12 次,目标值1.922 6,最优点(x1,x2)∗=(0.713 7,0.433 1).按第4 种情况处理,迭代9 次,目标值最优点值相同.第4 种处理方式的迭代次数更少.算例1 的目标函数等值线及约束可行域如图1 所示,星号点为最优点.

图1 算例1 的目标函数等值线及可行域Fig.1 Contour lines of the objective function and feasible region of example 1

2.2 算例2: 位移约束下连续体拓扑优化问题[19-21,28]

本算例以多工况位移约束下结构重量极小化结构拓扑优化问题为例,比较MMA 算法[6]与本文提出的DP-EM 算法的计算效率.算例数据如下.

如图2 所示,基结构尺寸为240×120×1 的平面体,材料弹性模量为E=1,泊松比为0.3.左右边界固定,工况1: 集中载荷F1=-1 竖直向下作用于上边界中点;工况2: 集中载荷F2=1 竖直向上作用于下边界中点(力以竖直向上为正).计算网格为240×120 个正方形单元.初始位移为工况1 沿集中载荷F1方向位移为-5.156,工况2 沿集中载荷F2方向位移为5.156 (位移方向竖直向上为正).位移约束为:工况1 时约束集中载荷F1方向位移大于等于-15,工况2 时约束集中载荷F2方向位移小于等于15.收敛精度取0.01.

图2 算例2 结构力学简图Fig.2 Mechanical diagram of example 2

使用MMA 算法经过80 次迭代收敛,历时247.904 s,最优点结构体积比为24.88%,上下结构边中点处约束点位移分别为-15.001 和15.001,最优拓扑图形如图3(a)所示.使用DP-EM 算法经过75 次迭代收敛,历时65.435 s,最优点结构体积比为23.76%,上下结构边中点处约束点位移分别为-14.999 和14.999,最优拓扑图形如图3(b)所示.MMA 算法的用时是DP-EM 算法的3.789 倍.结果显示DP-EM 算法具有更高的求解效率.

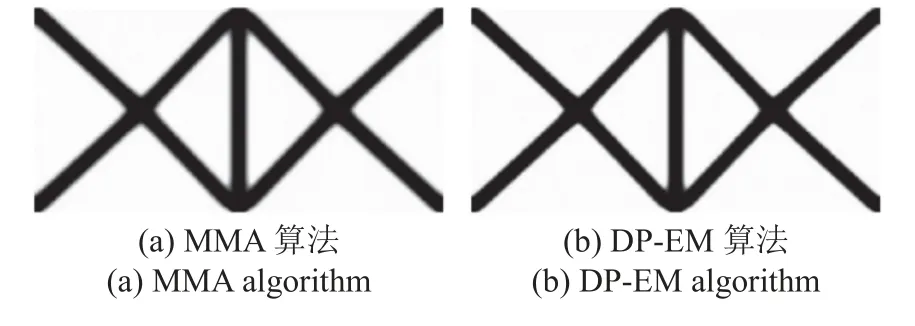
图3 算例2 最优拓扑Fig.3 Optimized toplolgies of example 2

2.3 算例3: 应力约束下连续体拓扑优化问题[29-31]

算例3 的基结构及载荷与算例2 相同,只是为了避免集中力作用导致的应力集中,将集中载荷分散布置在相邻的3 个节点上.Mises 应力约束小于或等于0.3.

取用本文算法,迭代66 次收敛,最优点体积比15.42%,最优拓扑图形如图4 所示.各工况的最大Mises 应力为0.295 7,两个工况下的Mises 应力分布图如图5 所示,满足应力约束条件.

图4 算例3 最优拓扑Fig.4 Optimized toplolgy of example 3

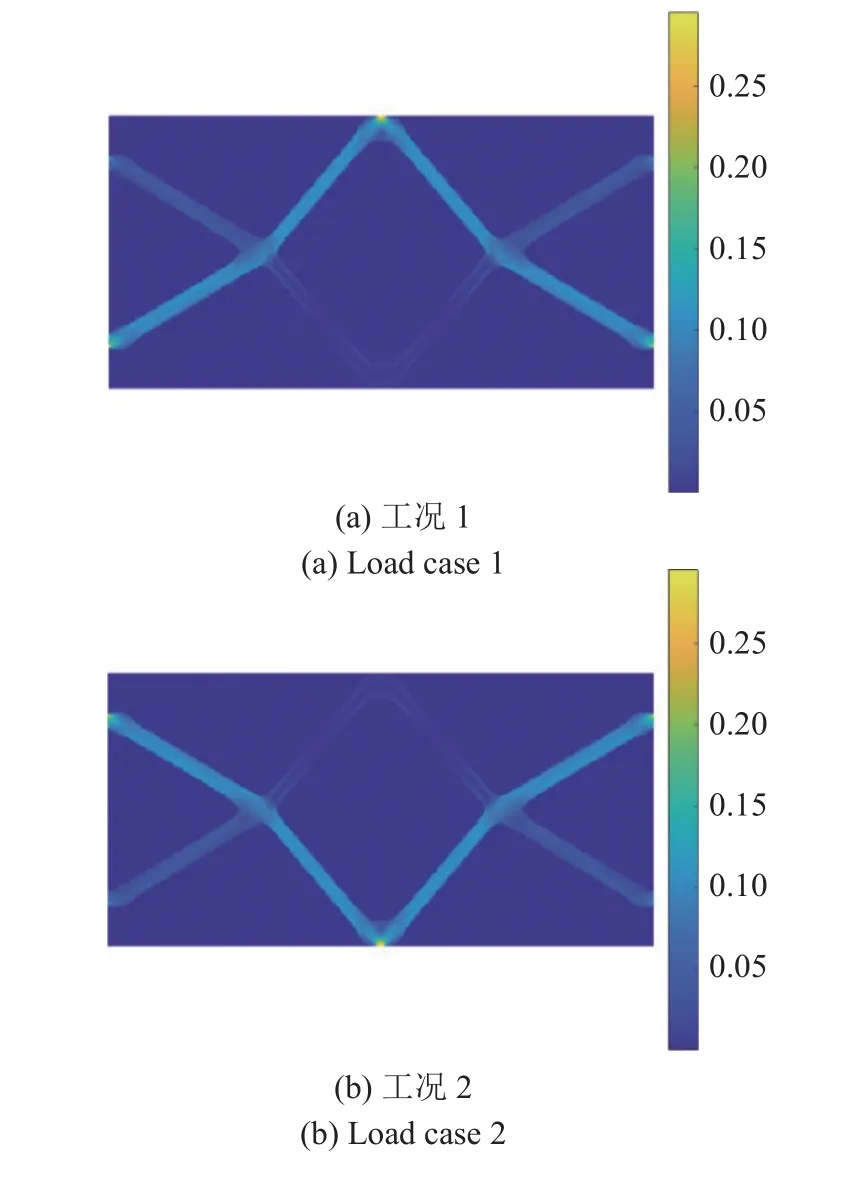
图5 算例3 Mises 应力分布Fig.5 Mises stress distributions of example 3

比较算例2 可知,位移约束与应力约束下的结构拓扑优化得到的最优拓扑是不相同的.

2.4 算例4: 疲劳约束下连续体拓扑优化问题[30-31]

如图6 所示,材料弹性模量为E=2.1×105MPa,泊松比 ν=0.3,材料对应于循环次数1.0×106的疲劳极限为 σs=250 MPa,基结构为300 mm×100 mm×10 mm 的平面体,划分为300×100 个正方形单元.基结构的左边界固定,正弦形式循环载荷F=7500 N且均值为零,相位角为零,作用于基结构右边界的中心点,为了避免应力集中将载荷施加在3 个节点上.疲劳寿命约束为大于或等于 1.0×105次.巴士昆公式σ=AL-m中,σ 为疲劳循环下的材料应力,L为对应的疲劳寿命,A与m为材料给定的常数量,此例中取值为m=0.10,A=995.3 MPa,S-N曲线如图7 所示.

图6 悬臂结构的分析优化模型Fig.6 Model of the cantilevel structure for analysis and optimization

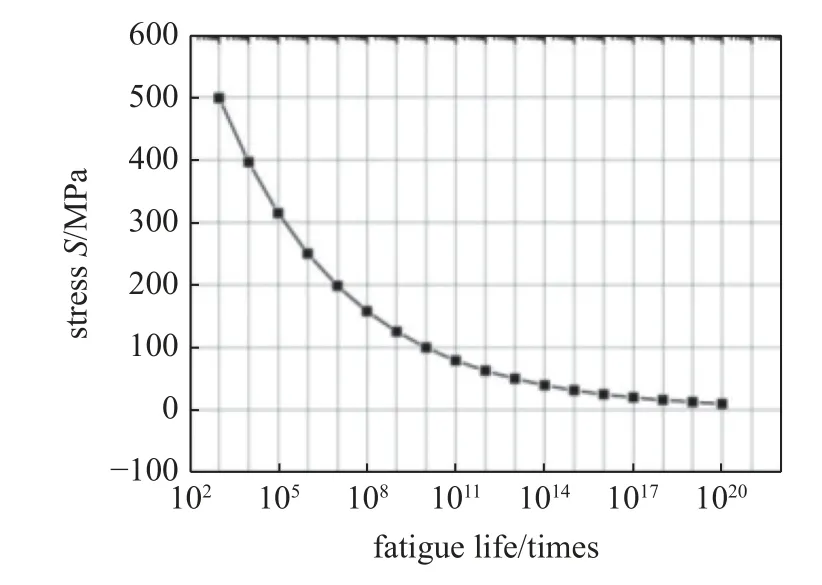
图7 m=0.10,A=995.3 MPa 材料的S-N 曲线Fig.7 S-N curve for the material with m=0.10,A=995.3 MPa

取用本文算法,经过62 次迭代收敛,最优体积比为39.73%,最大疲劳寿命为99 163 次.得到的最优拓扑如图8 所示,对应的疲劳寿命以10 为底的对数分布如图9 所示.

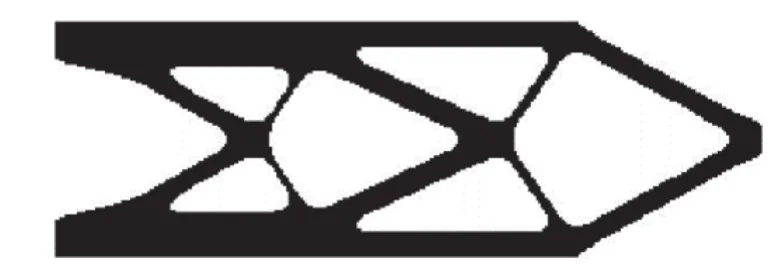
图8 算例4 最优拓扑Fig.8 Optimized topology of example 4

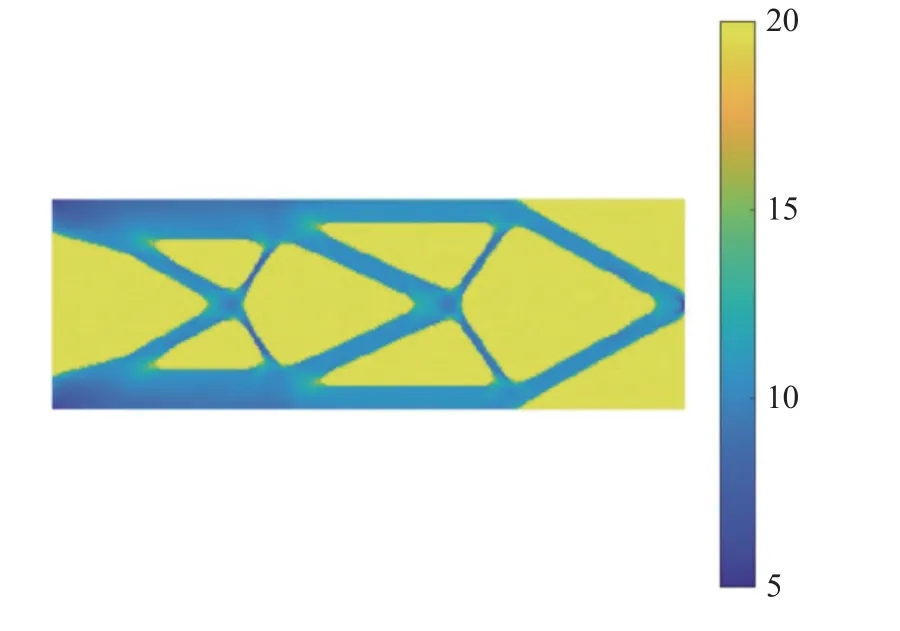
图9 算例4 最优时疲劳寿命分布Fig.9 Fatigue life distribution of of the optimized topology of example 4

2.5 算例5: 破损-安全拓扑优化问题[32]

如图10 所示,基结构为160×100 的平面体,厚度为1,材料弹性模量为1,泊松比为0.3.左边界固定,一集中载荷F=1 作用于右边界中心位置.采用25×25 的正方形作为结构局部破损模式,如图11中白色和灰色正方形所示,采用无缝平铺的结构破损状况预估分布模式,右边界附近区域为保留不发生破损的区域(如图11 所示方格子图案填充部分).有限元网格为160×100 个正方形单元,位移约束条件为A点的竖直向下位移值小于120.

图10 算例5 力学模型Fig.10 Mechanical model of example 5

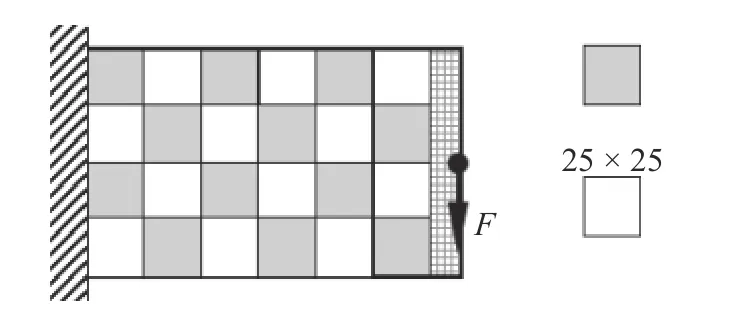
图11 算例5 的破损区域及其分布Fig.11 Fail regions and their distribution of example 5

不考虑破损-安全,按传统安全理念进行拓扑优化,得到的最优点体积比为18.40%,最优拓扑如图12(a)所示,最优点时约束点位移值为-119.9,满足位移约束条件.考虑破损-安全的结构拓扑优化最优点体积比为38.12%,最优拓扑如图12(b)所示.可以看出,考虑破损-安全之后得到的结构体积比更大,结构拓扑更复杂,但结构可满足所有破损情况下的安全.图13 为部分破损工况下的结构拓扑图及位移,表1 为最优点时所有各破损工况位移约束点的位移值,表中各行列数据均与图11 中的破损工况位置一一对应,例如表中的第1 行第1 列数据(-120.0)对应于图11 中第1 行第1 列破损位置发生破损,如图13(a)所示.可以看出有些破损工况是关键约束,有些破损工况不是关键约束,但所有破损工况均满足位移约束条件.

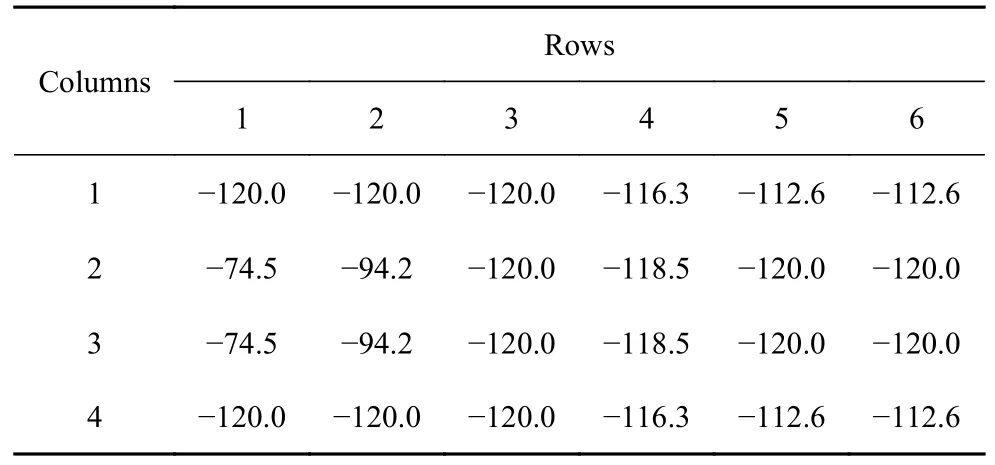
表1 算例5 最优点时各破损工况对应的约束点位移值Table 1 Displacements at constraint point for all failure cases at optimization of example 5

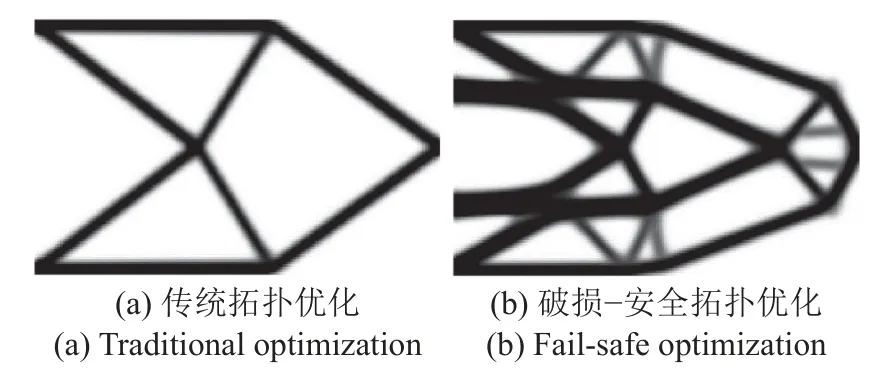
图12 算例5 最优拓扑Fig.12 Optimized toplolgies of example 5

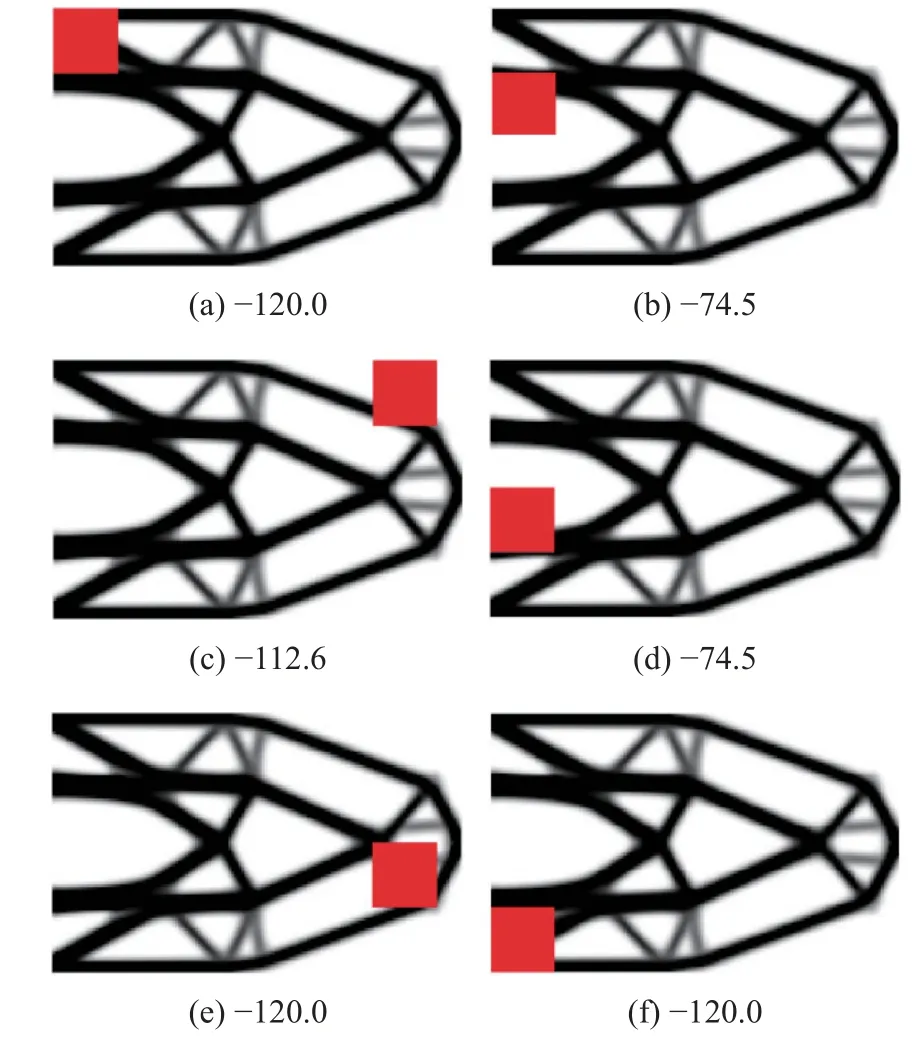
图13 算例5 带破损区域的最优拓扑及对应最优点时约束位移值Fig.13 Optimized toplolgies with failure regions and their constraint displacements of example 5

3 结论

我们团队以往经常把对偶规划用于结构优化的建模和求解,尤其用于结构拓扑优化问题,以提高求解效率,不过那时建立对偶规划的海赛阵,均为对个案的推导.

本文阐述了普适的处理方法,针对一类变量可分离凸规划模型,给出了4 种处理方法: (1)对偶变量迭代逼近法;(2)指数函数形式的解法;(3)幂函数形式的解法;(4)基于变换的精确解法.其中方法(1)和方法(4)是普适的方法,由于方法4 不需要采用迭代逼近的近似求解,比方法1 的求解效率更高.而方法2 和方法3 则示例了当函数形式给定后,依据具体的函数形式,同样可以给出直接解法,而不需要如方法1 中采取迭代解法.

不同于以往变密度法或ICM 方法中针对某一具体惩罚函数或过滤函数形式所建立的优化模型给出个案的求解公式及算法,本文针对一类变量可分离凸规划模型所阐述的普适处理方法,对文献[28]的DP-EM 方法进行了推广,从原来的只处理幂函数形式推广为可处理任意函数形式,因而保证今后惩罚函数或过滤函数采取不同函数形式时,优化模型的求解有一套普遍适用的可靠理论和算法.本文所提出方法相比广泛使用的MMA 方法具有更高的求解效率.这说明理论高度的提升会导致更有效和广泛的应用前景.相信本文的工作也会对于同行有借鉴作用.

附录A

以下列举基于ICM 方法建立的位移、应力、疲劳等约束下结构拓扑优化模型,以及考虑破损-安全的结构拓扑优化模型.

(1)位移约束连续体结构拓扑优化[19-21,28]

采用幂函数形式的过滤函数,单元重量及单元刚度用过滤函数识别

其中wi及ki为单元重量及单元刚度阵,及为单元固有重量及单元固有刚度阵.fw(ti)=(ti)α及fk(ti)=(ti)β分别为单元重量及单元刚度的幂函数形式过滤函数.

结构总重量表达为

其中N表示单元拓扑设计变量的总数.

位移利用莫尔定理表达为

用ICM 法建立的拓扑优化模型表示为

式中t=(t1,t2,···,tN)T是单元拓扑设计变量向量表示第j号位移约束的上限.

(2)应力或疲劳局部性能约束连续体结构拓扑优化[30-31]

对结构重量(或体积)、结构局部性能如应力或疲劳寿命等,均用过滤函数进行识别

式中,fw(ti)及fψ(ti)分别为结构重量(或体积)及结构性能如应力或疲劳寿命等的过滤函数,及分别为结构固有的重量(或体积)及结构性能如应力或疲劳寿命允许值等.

将N个约束应用K-S 函数进行集成,得到基于K-S 函数集成的局部性能约束优化模型

(3)考虑破损-安全的连续体结构拓扑优化[32]

应用ICM 方法,建立的结构拓扑优化模型为

其中,t为拓扑设计变量向量;V(t,Φ)为结构失效状况集合Φ中所有结构失效状况中体积最大值;ujls(t)为结构失效状况集合 Φ 中第s号结构失效状况 Ωs在第l的载荷工况下的第j号位移约束函数,为第j号位移约束值;J为位移约束总数,L为载荷工况总数;为防止有限元分析时总刚度矩阵奇异而设置的拓扑变量下限值.

结构总体积及位移约束的显式化与1 中的式(A1)～式(A4)类似.在此不再重复.