内爆炸载荷下泡沫铝夹芯圆管塑性动力响应及能量耗散机理1)

张天辉 刘志芳 雷建银 王志华 李世强

(太原理工大学机械与运载工程学院,太原 030024)

(太原理工大学应用力学研究所,太原 030024)

引言

金属与多孔材料结合构成的结构-功能一体化材料具有吸能性好、抗冲击性强和轻质等优点.在民用和军事领域得到广泛应用[1-9].

长期以来,关于冲击载荷作用下的结构变形机制和吸能特性的研究和取得的成果,已形成了基本的理论分析框架,也提出不同的实验测试方法和数值计算模型[5,10-13].泡沫铝方形夹芯板在爆炸载荷下动态响应的实验测试和数值模拟研究表明: 泡沫芯层的能量吸收占比较大,且随芯层密度和厚度的增大,能量吸收占比也随之增大[5].为考虑爆炸载荷作用下夹芯结构的动力响应及分层梯度泡沫芯层分布对屈服轨迹和抗爆性的影响,可分别应用边界屈服和内切屈服准则建立变形响应的近似解.实验测试和数值模拟结果证明: 前者得出的结果与实验测试和数值模拟结果吻合较好,后者较差[8].爆炸载荷作用下的3 阶段理论模型考虑夹芯梁的一维流固耦合问题及结构的塑性弯曲和拉伸变形[14].刚塑性模型的假设多用于夹芯梁、板和壳的动力响应的分析,得到的理论预测值略高于实验测试和有限元模拟结果[15-18].

如何考虑梯度夹芯结构层间相互作用及结构的压缩变形机制是理论建模的关键[19-24].材料迎爆面上受均布载荷作用的理论假设适用于起爆中心与结构距离较大的情形.在近距离爆炸载荷作用下须考虑结构动态响应的非线性特征.内爆载荷作用下泡沫夹芯圆柱壳结构动力响应分析属于具有自由端边界的近距离爆炸问题.涉及到强时空非线性和不均匀性[25-29].梯度泡沫铝芯层圆柱壳的动力响应的有限元模拟表明: 在外管发生变形之前,梯度芯层压溃变形表现出由低相对密度到高密度的逐层发展模式.而且梯度芯层的压缩量大于均匀芯层的压缩量[30].内爆载荷下梯度泡沫夹芯管的一维动力学模型将夹芯管的变形过程分为3 个阶段: 流体与结构相互作用阶段、芯层压缩阶段和外管的变形阶段.分析表明: 炸药量、芯层梯度与面板厚度对夹芯管动态响应产生影响;梯度泡沫夹芯管的吸能性能受内管壁厚的变化影响较大,受外管壁厚的变化影响较小;芯层的排布方式可改变结构的吸能性及外管变形特征[31].内爆载荷下夹芯圆管动态变形的4 阶段理论模型考虑了外管未变形阶段芯层在加速、减速运动下的压缩、外管变形阶段芯层二次压缩和芯层密实化后结构整体变形的4 个变形过程.该理论解析模型能够分析和解释芯层压缩和外管的变形阶段应力的传播过程.此外,基于相应的参数分析可对夹芯圆管进行进一步的优化设计[32].

已有内爆载荷作用下泡沫夹芯圆管动态响应的研究主要基于一维分析模型.但实际中人们更关注整体结构的响应.这就需要考虑环向膜力和轴向弯矩对夹芯圆管的变形行为和吸能机制的影响.

作者所在课题组近期开展的研究工作涉及到泡沫铝芯层轴向梯度分布对夹芯圆管的动态变形和吸能机制的影响[29].在实验测试和数值模拟研究基础上,假设内爆载荷具有空间呈三角形分布、时间服从指数衰减规律,建立考虑环向膜力和轴向弯矩对夹芯圆管动态响应的纵截面二维分析模型.通过选取不同几何参数,以无量纲形式确定了外管中心线的挠度,研究了夹芯圆管的内爆压缩变形行为.如何在确定结构变形行为的基础上进一步构造描述结构能量吸收机制的分析模型,并通过合理结构参数的选取获得比吸能较大、圆管中心线挠度较小的最优结构是一个亟待解决的问题.本文基于不同几何参数和药量的泡沫铝夹芯圆管的内爆实验观察,确定圆管试件的变形模式.在考虑环向膜力和轴向弯矩的作用下,提出描述内爆载荷作用下内外管变形及吸能量机制的理论模型.基于三维Voronoi 算法构建了夹芯圆管有限元模型,研究几何参数对结构的变形模式和抗爆性能的影响.

1 实验研究

实验试件的材料参数如表1 所示.不锈钢的材料参数根据ISO 6892-1:2009 标准,使用拉伸测试方法获得.利用线切割技术从100 mm 厚,相对密度为15%的闭孔泡沫铝板上切割出泡沫铝芯层,泡沫铝基体材料为铝合金.采用图1 所示的实验装置进行泡沫铝夹芯圆管内爆实验.实验装置由球形乳化炸药、泡沫填充夹层圆管、基座和支架组成,底座和支架与地面平行放置.为了避免爆炸后地面反射冲击波的影响,泡沫填充的夹层圆管位于高度为1 m 的基座上.利用支架来保证炸药在试件中心位置起爆,球形乳化炸药的爆炸由雷管触发.将内外管与泡沫铝芯层组装到一起得到泡沫铝夹芯圆管试样,泡沫铝与内外管之间无黏结.试件总高度L=100 mm,芯层壁厚为hC,内外管壁厚分别为hI和hE.实验参数如表2 所示,其中,RI和RE分别为内外管半径,W为乳化炸药质量.芯层壁厚hC=RE-RI-hI由内外管半径和内管壁厚确定.

图1 实验装置示意图Fig.1 Schematic of the experimental setup

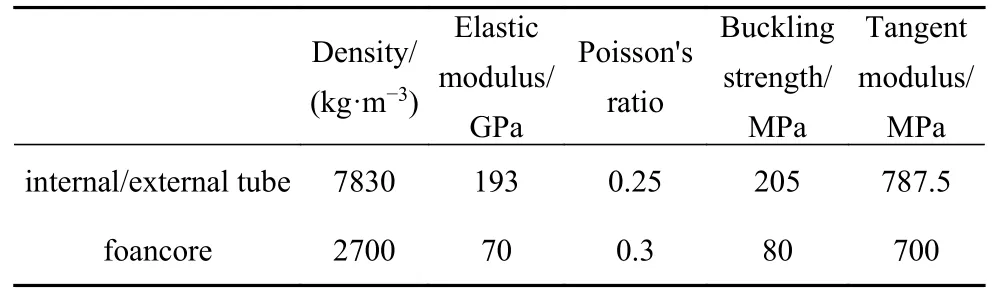
表1 材料参数Table 1 Material parameters

表2 实验参数Table 2 Experiment parameters

将表2 中7 组试样进行内爆炸实验,所得内外管跨中挠度如表3 所示,UI为内管挠度,UE为外管挠度.当炸药质量相同时(Test 1-1 与Test 2-1、Test 1-2 与Test 2-2、Test 1-3 与Test 2-3),增大外管半径使内管跨中挠度增大,芯层压缩量增加,且外管跨中挠度减小.

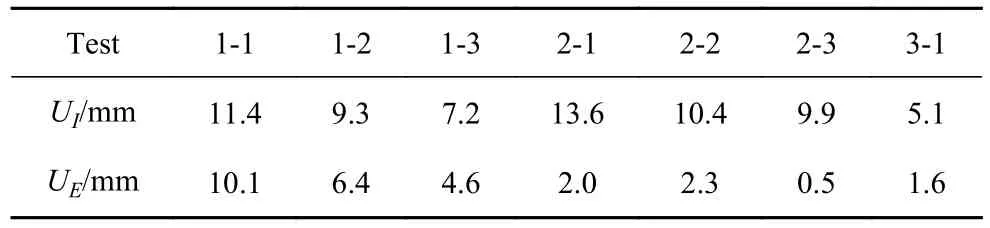
表3 实验结果Table 3 Experiment results

图2 给出了试件1-2 的最终变形模式.从图中可以看出,内外管的最终变形分为3 个区域: 塑性变形较大区域;围绕塑性铰刚性旋转区域和边界未变形区域[29].可见: 内外管的变形模式与文献[33]报道的侧向爆炸载荷作用下薄壁圆柱壳纵截面的变形模式相似;芯层的压缩使内外管具有不同的未变形边界.这个观察结果为分析夹芯圆管在内爆载荷作用下的变形机制提供了科学依据.

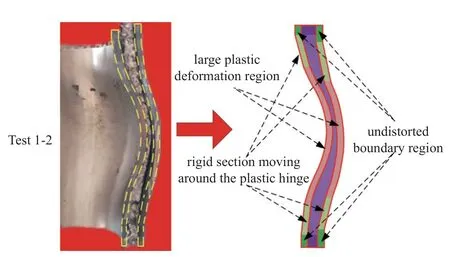
图2 试件1-2 实验结果Fig.2 Experiment result of Test 1-2

2 理论分析

泡沫铝夹芯圆管在内爆载荷下的动态响应可分为3 个阶段: 爆炸载荷与内管相互作用,具有初始速度的内管压缩芯层,芯层达到密实化后外管变形.取模型的轴向单位面积进行分析,其几何尺寸及各个阶段变形的受力分析如图3 所示.其中,l为模型总高度的1/2,NI,NC和NE分别为内管、芯层及外管的环向膜力,Mx为轴向弯矩.

图3 结构变形过程: (a)轴向截面选取;(b)爆炸载荷作用于内管;(c)具有初始速度的内管压缩芯层;(d)外管变形Fig.3 Deformation process of the structure: (a)Axial section selection;(b)Blast loading interacting with the internal tube;(c)Internal tube with the initial velocity impacting the foam core;(d)External tube deformation

假设爆炸载荷在轴向空间呈三角形分布,在环向空间为均匀分布,在时间上为指数衰减.根据Henrych[34]对临近爆炸载荷的分析,假设内爆炸下产生的脉冲载荷为

其中,τ 为爆炸载荷持续时间,P0为爆炸载荷超压峰值.关于爆炸载荷超压峰值及超压持续时间的计算方法,采用下式进行计算[35]

其中,R为炸药爆心到内管表面的距离,WT为TNT当量.根据山东圣世达化工有限责任公司提供的乳化炸药当量实验测试数据,实验用乳化炸药与TNT炸药质量关系式为WT=0.6W.

基于泡沫夹芯圆管的变形特性,建立分析模型时采用了以下假设:

(1)内外管假设为刚塑性模型,当材料达到屈服强度时发生塑性变形,卸载后结构不发生形变恢复;

(2)忽略应变率和应变强化的影响,简化理论推导过程,但会造成一定误差;

(3)假设结构在响应过程中以塑性变形为主,忽略内外管和芯层的破坏失效;

(4)在芯层压缩过程中,假设芯层在压缩过程中以塑性变形为主并以恒定的平台应力被压缩.

2.1 第1 阶段: 爆炸载荷作用于内管

根据图3(a)中脉冲载荷函数分布及公式(1)中的函数假设,爆炸载荷作用于内管时内管获得的总冲量为

假设速度沿轴向分布为v0(1-x/l),内管的动量为

其中,mI为内管的单位面积质量.结合式(7)和式(8)得出内管初速度

2.2 第2 阶段: 芯层压缩

如图3(b)所示,根据爆炸载荷的大小,内管分为变形和未变形区域.当P0(1-x/l)≤NI时,内管不变形,当P0(1-x/l)>NI时,内管发生变形并压缩芯层.内管膜力NI=σYIhI,其中,σYI为内管屈服强度.定义轴向方向的单位环向截面超压=P0(1-x/l),在内管未变形区域,和NI存下以下关系

假设内管受爆炸载荷产生的冲击力与式(1)中的超压在轴向的分布相同,内管的速度场近似等效为vI(x)=(1-x/l),uI为内管在初始位置随时间变化的位移.在芯层压缩阶段,内管运动的微分方程为[36]

其中,Qx为结构的剪力,σpl为芯层平台应力,Nθ=NI+NC=N1,NC=σYChC为芯层环向膜力,σYC为芯层屈服强度.当x=0 时,剪力Qx=∂Mx/∂x=0 以满足对称性要求,且Mx=-M0以形成环向塑性铰,M0为内管在纯弯曲作用下的塑性弯矩.在x=l(1-NI/P0)=x1处,Mx=M0.因此,式(11)可变为

初始条件:uI(0)=0,=P0τ/mI.因此可得

式(14)可用于确定芯层压缩阶段某一时刻内管的位移和速度.在芯层压缩过程中,若芯层压缩至密实化,结构进入外管变形阶段.因此,需要对内管最终位移与芯层量对比来确定结构在变形过程中是否进入外管变形阶段.根据Li 等[37]提供的相对密度为15%泡沫铝在准静态压缩载荷下的应力-应变曲线和Fan 等[38]对于多孔结构在压缩过程中密实化的研究,确定15%泡沫铝的密实化应变 εd为0.5.取公式(14)中=0,则内管在芯层压缩阶段的最终跨中挠度

若uI1≤hCεd,外管不发生变形,泡沫夹芯管在芯层压缩阶段运动结束.若uI1>hCεd,泡沫芯层在第2 阶段达到密实化,外管开始变形.此时式(15)中所得的内管挠度没有考虑到外管变形的影响,对内管的最终挠度需进行进一步分析.

2.3 第3 阶段: 外管变形

若外管发生变形,需确定芯层达到密实化时对应的时间,取uI=hCεd代入式(14)中,则

在外管变形阶段,芯层已达到密实化,内管继续做减速运动.在外管变形阶段,内管和泡沫芯层的运动使外管开始做加速运动.当外管速度与内管和芯层速度相同时,结构做整体减速运动直至变形结束.以内管的运动为研究对象,内管的加速度为

其中,N2=NI+NC+NE,外管膜力NE=σYEhE,σYE为外管屈服强度.初始条件:uI2(t2)=hCεd,(t2)=-k1t2+P0τ/mI.结合式(18)和外管变形阶段的初始条件得出内管在第3 阶段的速度和位移

当内管速度为0 时,结构整体运动结束,取=0代入式(19)中可得出结构变形结束所需时间

在理论计算中忽略了内外管和芯层的耦合关系,因此,外管的位移uE=uI-hCεd.内管对应的变形轮廓

取uf=hCεd代入式(22)中可得外管轴向变形边界

根据动量守恒定律,在外管变形阶段,内/外管和泡沫芯层的共同速度为

其中,mC和mE分别为泡沫芯层和外管的单位面积质量.结合式(17)和式(19),得到内外管和泡沫芯达到此速度所需的时间.

2.4 能量吸收机制

基于上述对于泡沫铝夹芯圆管在内爆炸载荷下的3 阶段变形分析,结合结构在响应过程中动能的变化及环向膜力和轴向弯矩的作用对其在响应过程中的能量吸收机理进行理论分析.如图3(a)所示,以泡沫铝夹芯圆管轴向单位面积为研究对象,内管的初动能为

当内外管和芯层达到共同速度之后,结构开始做整体的减速运动.由动量守恒得出内外管和芯层的共同速度v1

根据内外管在轴向方向上的变形位置x1和x2可以得出内外管达到共同速度时的动能

内外管和芯层达到共同速度时泡沫铝夹芯圆管轴向单位面积的能量吸收E1=-.

在结构整体运动阶段,由环向膜力和芯层动平台应力所消耗在结构中的轴向单位面积的总能量E2为

综合考虑泡沫铝夹芯圆管受到的环向膜力和轴向弯矩的影响可以得出,结构在整个运动过程中轴向单位面积吸收的总能量表达式

根据表2 中实验所得内外管最终挠度可知,泡沫铝夹芯圆管在内爆炸载荷作用下变形较小.在内外管和芯层达到共同速度到整个泡沫夹芯管达到最终变形的过程中,由内外管和芯层的弯矩引起的能量吸收很小,可忽略不计.因此,式(32)可改写为

3 数值模拟及算法验证

3.1 有限元模型

采用商业软件ABAQUS/Explicit 有限元程序进行数值模拟.基于结构和载荷的对称性,建立了泡沫铝夹芯圆管的1/8 模型,如图4 所示.1/8 模型的边界条件定义为: 结构顶部为自由边界,在其他边缘施加对称边界条件(X-Z面约束Y方向位移和X,Z方向转角,Y-Z面约束X方向位移和Y,Z方向转角).内外管采用8 节点线性实体单元(C3D8R),利用三维Voronoi 算法[39]构建相对密度为15%泡沫铝芯层,采用传统的3 节点壳单元(S3R)进行网格划分.为保持结构变形的稳定性,在ABAQUS/explicit 中采用罚函数方法来加强约束,内外管与泡沫芯层之间定义硬接触(hard contact),摩擦系数设置为0.02[39].采用表1 中的内外管和芯层的材料参数进行数值模拟.泡沫铝芯层采用双线性强化模型,内外管均为不锈钢材料,在模拟中使用各向同性随动强化塑性模型,应变率 ε 采用Cowper-Symonds 模型,屈服应力为 1 +(ε/C)1/q,其中C=100 s-1,q=10[33].球形爆炸载荷采用ConWep 算法来模拟结构变形.芯层和内外管的网状尺寸定义为0.5 mm,进一步的细化并没有明显提高计算结果的精度.

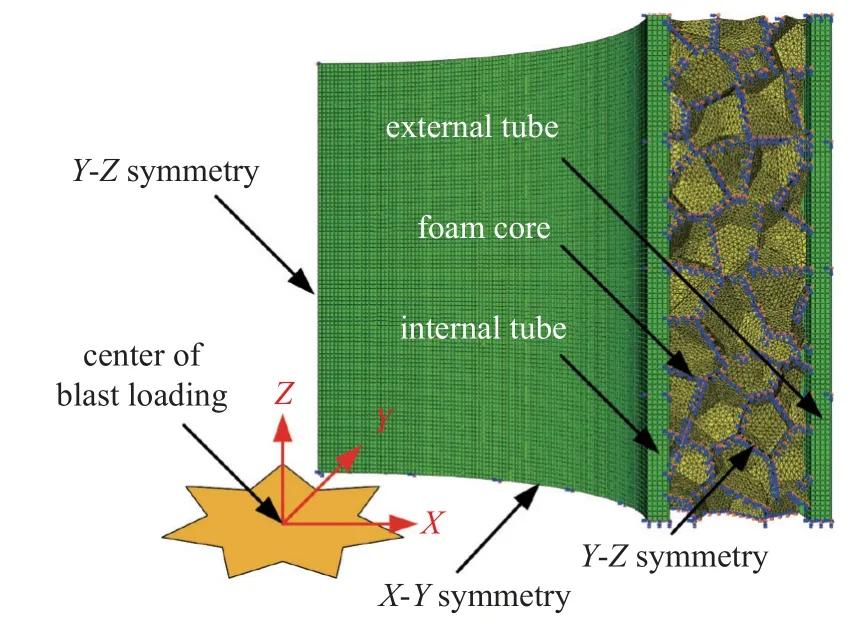
图4 有限元模型Fig.4 Finite element model

3.2 模型验证

图5(a)为试件1-2 和试件2-3 实验与数值模拟最终变形模态对比,数值模拟结果具有明显的3 个变形区域,且内外管的未变形边界不同,与图1 实验模态中观察到的结果一致,二者吻合较好.以内外管中点挠度为对象来验证数值模拟与理论分析模型的有效性,所得结果如图5(b)所示.

图5 模型验证Fig.5 Validation of the model

在数值模拟中忽略了泡沫芯层在变形过程中的破坏以及内外管与芯层之间的耦合作用,低估结构的强度,导致大多数模拟结果略高于实验值.在理论分析过程中,假设泡沫芯层达到密实化后,外管开始变形,已经密实化的芯层不再进一步发生断裂和失效破坏.此外,在结构3 阶段变形过程中,采用解耦的办法进行逐步分析,忽略了内外管与芯层之间的流固耦合作用.且理论分析中忽略了应变率和应变强化的影响,大多数理论预测的中点挠度略高于实验结果.

4 结果与讨论

4.1 参数无量纲化

根据结构的几何模型和材料强度进行无量纲参数的定义

将无量纲参数代入式(13)和式(18)可得

将内管和外管的跨中无量纲挠度定义为

结合式(16)、式(20)、式(21)、式(35)和式(36)可得内外管中点无量纲挠度的最终表达式

将无量纲参数代入式(25)、式(27)和式(28)并消除结构质量的影响,可得结构在各响应阶段的比吸能

4.2 参数分析

图6 列出了给定内外管和芯层材料参数的泡沫铝夹芯圆管在TNT 药量为30 g 下外管中点无量纲挠度随结构壁厚变化的响应体.可以看出,利用泡沫芯层和内外管的壁厚可以有效地评估外管的无量纲挠度.内管壁厚对外管中点挠度影响较大,芯层和外管壁厚对外管中点挠度影响较小.当芯层和外管壁厚一定时,外管中点挠度随内管壁厚的增加而减小.当 β1=0.053,β2=0.105,β3=0.053 时,外管无量纲中点挠度出现最大值,为0.3.由于外管挠度随几何参数的变化呈单调趋势,因此,需结合总能量吸收来进一步得出结构的最优构型.

图6 外管无量纲中点挠度响应体Fig.6 Response volume of nondimensional midpoint deflection of the external tube

取内管半径RI=38～44.5 mm,外管半径RE=44.5～54 mm,内管壁厚hI=2～4 mm,外管壁厚hE=2 mm,在TNT 药量为18 g 来研究结构比吸能和外观中点挠度的最优解,所得结果如图7 所示.当内管半径RI=38 mm,外管半径RE=44.5 mm,内管壁厚hI=2 mm 时比吸能最大,为2.39 kJ/kg,此时对应的外管无量纲中点挠度为0.13.内管壁厚及内外管半径的变化使结构在既定的炸药质量下出现了许多外管无量纲挠度为0 的几何构型.在外管无量纲挠度为0 的条件下,内管半径RI=38 mm,外管半径RE=53.5 mm,内管壁厚hI=2 mm 的比吸能最大,为1.15 kJ/kg.根据图7 所列出的数据,可以在实际工程中给定的外管挠度条件下找出比吸能最大的几何构型.此外,也可以在给定比吸能条件下找出外管挠度最小的结构.

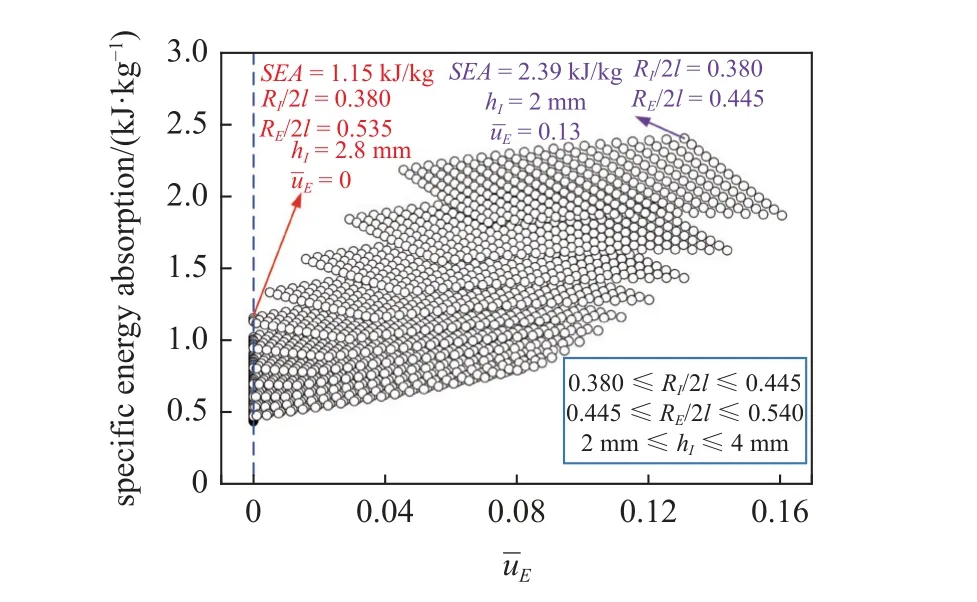
图7 比吸能与外管无量纲挠度最优解Fig.7 The optimal solution of specific energy absorption and nondimensional midpoint deflection of the external tube

4.3 梯度芯层

如图1 所示,芯层的相对密度沿轴向每20 mm变化一次.根据1/8 有限元模型的对称性,在数值模拟中相对密度 ρs1的高度为10 mm,如图8 所示.芯层的轴向梯度分布模型参数如表4 所示.其中,G0为非梯度模型对照组.

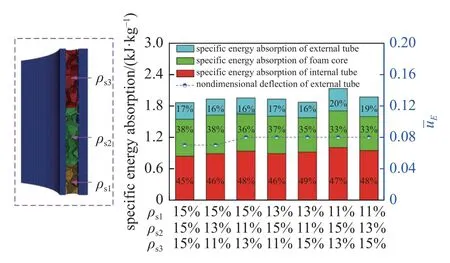
图8 不同泡沫芯层分布的比吸能和外管无量纲挠度Fig.8 Specific energy absorption and nondimensional deflection of external tube for various foam core distributions

表4 梯度模型参数Table 4 Graded model parameters

以内管半径RI=38 mm,外管半径RE=44.5 mm,内管壁厚hI=2 mm,外管壁厚hE=3 mm,TNT 药量为30 g 为基础来研究芯层轴向梯度分布对结构抗爆性能的影响,所得结果如图8 所示.G5 梯度模型具有最高的比吸能,且外管无量纲中点挠度与其他混合梯度结构相同,但芯层吸能占比仅为33%.对于G1 梯度模型,外管无量纲中点挠度低于其他轴向梯度分布结构,且芯层能量吸收占比为38%.

5 结论与展望

采用实验、理论和数值模拟相结合的方法,研究了泡沫铝夹芯圆管在内爆炸载荷作用下的动力响应.建立了泡沫铝夹芯圆管内爆炸响应的解析表达式.采用理论和有限元分析方法对泡沫铝夹芯圆管的动力学行为、变形机理和能量吸收进行了详细分析.详细讨论了外管半径、内外管壁厚、炸药量和芯层梯度分布对结构力学响应的影响.本文得出主要结论如下.

(1)理论分析模型与泡沫铝夹芯圆管在内爆炸载荷作用下的实验和数值模拟结果吻合较好.所提出的动态显示算法具有较好的可靠性.

(2)通过内爆炸实验得到了泡沫铝夹芯圆管在内爆炸载荷作用下3 个不同变形区域: 塑性变形较大区域、围绕塑性铰刚性旋转区域和边界未变形区域.

(3)内管壁厚对外管中点挠度影响较大,芯层和外管壁厚对外管中点挠度影响较小.通过改变结构的几何参数得出了结构比吸能和外管中点挠度的最优解集.

(4)在所有芯层轴向梯度分布的泡沫铝夹芯圆管中,芯层轴向分布由中心到边缘递减的梯度夹芯圆管模型的外管无量纲挠度最小,芯层能量吸收占比最大.

本文所建立的理论解析模型中,内外管在受载变形时假设为理想刚塑性模型.而基体材料本身存在应力强化过程,且泡沫铝夹芯圆管在受内爆炸载荷作用下的弹性变形效应[40]对结构的整体响应机制存在一定的影响,这也是所提出的理论预测值与实验存在误差的原因.关于如何结合基体材料的应力强化和结构的弹性效应来构建更为精确的动态显示理论计算方法可展开更为深入的研究.

文中未涉及关于径向梯度泡沫铝夹芯圆管在内爆炸载荷下的理论分析,径向梯度芯层压缩阶段需考虑每一层泡沫芯的相互作用,可以假设梯度芯层为解耦的逐层压溃模式[31].但如何确定径向梯度的每一层芯层的变形边界及应力波在梯度芯层中的传播规律是需要解决的重点和难点.