基于共振转换器的自主水下航行器动力学建模及减振降噪1)

张康宇 路 宽, 程 晖 傅 超 郭 栋

* (西北工业大学力学与土木建筑学院,西安 710072)

† (西北工业大学智能飞行器结构强度与设计研究所,西安 710072)

** (西北工业大学机电学院,西安 710072)

引言

近些年来,我国海洋军事发展迅猛,以鱼雷、潜艇等为代表的自主水下航行器(autonomous underwater vehicle,AUV)凭借其隐蔽性好、破坏威力大以及命中率高等显著优势,在海洋战争中扮演着“杀手锏”的角色[1-3].其高隐身技术是评价现代AUV 先进性的重要指标之一,研究显示此类系统辐射噪声每提高5 dB,敌方报警距离将提高50%,有效命中率缩减25%[4].AUV 本质上是一种内部高速旋转的水下航行器,主要由外部壳体和内部部件组成,壳体内表面附有加强环,内部含有螺旋浆、推进轴系、电机、轴承和连接结构等部件,其振动辐射噪声主要来源于内部动力电机,电机运行输出扭矩并通过推进轴系带动螺旋桨高速旋转,致使外界周围流场突变产生流动噪声;另一部分主要来源于螺旋桨与电机的振动通过连接结构传递至壳体从而带动外表面周围流体介质引起辐射噪声[5].

针对AUV 此类系统的减振降噪研究受到了海内外学者的广泛关注[6-8].美俄等国早在20 世纪中期就开展了相关技术的研究,并成功用于多种型号,起初的AUV 隔振技术主要采用特殊材料制成的结构添加至连接结构中,振动在传递过程中逐渐被吸收衰减.早期服役的MK46 采用了多个先进降噪技术,包括采用工程塑料作为螺旋桨的材料、采用“○”形橡胶圈对段间联接所用的箍环进行密封、自导头中的声换能器基阵以悬挂的方式固定于壳体,同时之间采用多层弹性材料连接[4].20 世纪70 年代,美国更为先进的MK48 通过在隔振座上安装自动驱动设备减小主动力装置振动向鱼雷壳体的传递,同时壳体内表面敷设阻尼材料,抑制壳体振动以此降低壳体的声辐射效率[3].MK54 在动力电机与壳体之间采用弹性软连接结构降低振动传递效率,均具有很好的噪声抑制效果[4].

国内对于AUV 声隐身设计的研究起步较晚,但近年来,许多学者就相关问题进行了广泛而深入的研究,在模型结构以及求解等基础研究中取得了一定进展[9-12].Pan 等[13]考虑了任意边界条件下受环肋加强的圆柱壳的振动特性.对于简支和其他边界条件,圆柱壳的位移函数分别采用三角函数和指数函数的表达式进行求解.Wei 等[14]采用波函数法对加肋圆柱壳的自由振动特性进行了分析.Zhao 等[15]用能量法计算了简支旋转复合材料加肋圆柱壳.他们在处理纵肋和环肋时,采用了平均分摊法和离散法,并且考虑了肋骨的偏心影响.刘扭扭[16]利用耦合有限元/边界元计算方法,建立桨-轴的半解析模型和有限元模型,通过模态分析及谐响应分析分析了桨-轴的纵向振动特性以及艇体基座弹性对桨-轴的纵向振动的影响,结合螺旋桨上的作用力谱,提出推进轴系纵向振动控制的目标频率.

目前在AUV 减振降噪领域,针对振源和被控对象,主要有消振、隔振、阻振、吸振和优化结构等方法,具体的包括主动控制[17],比如采用压电式作动器,基于正逆压电效应由闭环电路进行驱动控制[18];半主动控制通过调整装置的刚度、阻尼和质量等物理参数来协助主动控制实现振动控制[19],比如可调阻尼器、可调振动减缓器和液压减振器等[20].以上方法具有响应快,控制范围广等优点,但受限于控制力大小,被动控制广泛应用于舰体等大型和高速航行器[21-22].

共振转换器(resonance changer,RC)是一种利用流体介质的动态减振器件,最早由Goodwin[23]于20 世纪60 年代提出,发展于21 世纪,被广泛用于舰体等航行器轴向力传递的抑制.共振变换器由圆柱活塞和油腔组成,中间由细长导管相连,通过油腔内部液压油的压缩或膨胀在活塞处产生力的作用,经推导该力的数值大小可以振动方程的形式体现,通过RC 的结构参数设计得到最优等效质量、等效阻尼和等效刚度,使其固有频率等于系统共振频率以此达到反共振的目的[24].Paul 等[25]研究了当螺旋桨叶片通过非均匀伴流旋转时,推力的微小变化在螺旋桨处产生振荡,导致螺旋桨在叶频处产生轴向激励,使用RC 降低了振动传递和避免船体轴向共振的激励.Sascha 等[26]以RC 的等效刚度、阻尼和质量为设计参数,研究了表征整体辐射声功率的代价函数,通过应用基于梯度的优化技术找到代价函数的最小值,并采用伴随算子计算代价函数对设计参数的灵敏度,探究了螺旋桨振动引起的声辐射对共振转换器优化的影响以及叶片通过频率高次谐波幅值降低对控制性能的影响.胡泽超等[27]在推力轴承上集成RC 改变了轴系纵向振动的传递路径,衰减传递到基座的响应使轴系的固有频率避开螺旋桨叶频及其倍叶频激励力,从而实现了减振及调频的目的.

本文对鱼雷等AUV 系统进行了减振降噪研究,在模型建立过程中发现多数学者集中于圆柱壳体与内部旋转机械在流体介质中动力学特征的独立研究.在大多数研究中简单模型考虑了动力旋转机构的影响,对于复杂桨-轴-壳模型则忽略了旋转偏心激励,然而此类简化处理并不符合AUV 实际模型构成,不可避免地会影响其动力学特征.本文研究工作着重于AUV 减振降噪的关键技术问题,基于双梁系统建立了含有浆-轴-壳的精细化动力学模型,充分考虑了非线性轴承及其他连接部件的影响,对比线性弹簧与非线性轴承两种支撑下双梁系统的动力学响应,揭示了AUV 此类系统的动力学行为机理.以壳体声功率级作为代价函数并根据系统幅频响应特征,添加经过参数设计后RC 装置,结果显示能够大幅度降低系统共振响应幅值及振动辐射声功率级.

1 动力学模型及其振动声辐射场

1.1 有限元模型

AUV 舱段结构如图1 所示,考虑实际工况下的旋转特性,故采用轴对称模型.外部壳体的内表面附有加强环起到紧固作用,同时环上附有螺纹孔连接内部零部件,其内部包含动力电机、末端螺旋桨和中部推进轴系,使用3 个滚珠球轴承和线性弹簧连接至壳体,壳体通过3 个线性弹簧固定.

图1 水下航行器舱段结构示意图Fig.1 Schematic diagram of the AUV power cabin

根据各部件对系统振动辐射噪声影响重要度,将AUV 舱段简化为浆-轴-壳双梁模型.外部为耐压壳体,将其处理为内表面均匀分布矩形截面加强环的圆柱形空心梁,由于壳体及轴系的长径比分别为0.2 和2.5,因此均采用Timoshenko 梁[28].此外,耐压壳的端板相对于壳体在径向方向上的刚度可认定为是刚性的.内部推进轴系简化为实心梁,螺旋桨/轴系系统模块化物理模型如图2 所示.

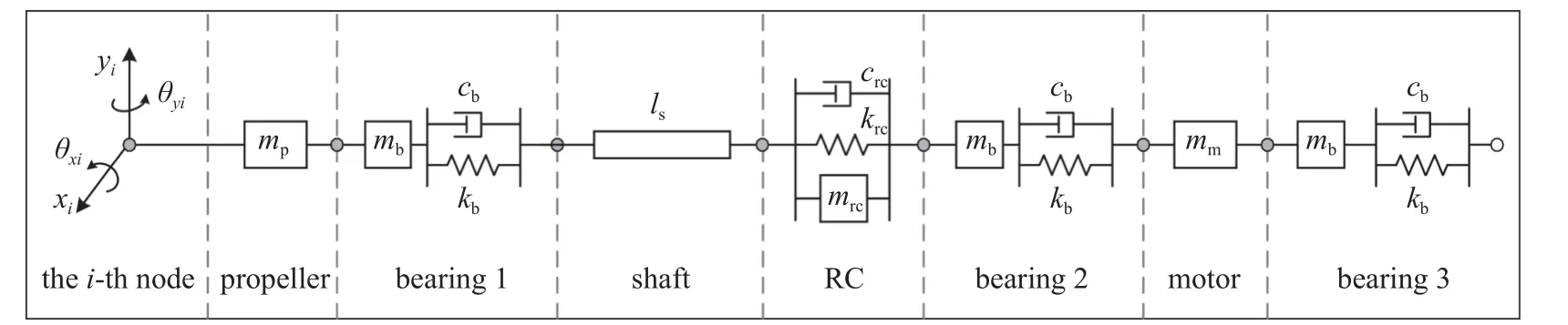
图2 螺旋桨/轴系系统模块化物理模型Fig.2 Modular physical model for the propeller/shaft system

图2 给出了AUV 动力舱段系统模型的全局坐标系o-xyz,原点建立在螺旋桨中心处.由于系统沿轴向的扭转角及其位移分量很小,可忽略不计[29],重点研究壳体在电机偏心激励和外部流体介质激励作用下的径向振动.推进轴系(均分为11 个节点)和壳体(均分为21 个节点)的每个单元节点具有沿径向水平o-x和径向竖直方向o-y的平移xi,yi和绕其转角 θxi,θyi4 个自由度,轴承单元节点具有沿径向水平和竖直方向的平移xi,yi2 个自由度.采用Lagrange法推导AUV 双梁系统的动力学微分方程,振动系统的第二类Lagrange 方程可表示为

系统总动能由质量点的平移动能和旋转动能组成,具体可表示为

其中,mi,Ji为推进轴系与壳体的节点质量和极惯性矩,mj为轴承外环的节点质量.值得注意的是,具有一定偏心距的螺旋桨和电机被简化为质量点附加到推进轴系的对应节点上.

系统总势能包含推进轴系和壳体的变形能,轴承外环支撑弹簧和壳体支撑弹簧变形储存的能量,可表示为

其中,Ks表示推进轴系和壳体组成的刚度阵,Kb表示轴承外环和壳体相连弹簧的刚度阵;nc,kc表示壳体支撑弹簧的数量和刚度大小,uc为弹簧两端壳体与轴承外环的相对位移量.

仅考虑推进轴系的Rayleigh 耗散能,总耗散能可表示为

其中,Cs为推进轴系的阻尼阵.

系统在各节点处受到的合力为F,主要包括各节点的重力、螺旋桨和电机的偏心力,轴承非线性恢复力.系统重力Fg=mkg0平均分配到各节点上,g0表示重力加速度.偏心力大小表示为

其中,mp,ep为螺旋桨的质量和偏心距,mm,em为电机的质量和偏心距.

如图3 所示,轴承主要由内环、外环、滚动球和保持架组成,轴承内环固定在轴上,外环通过线性弹簧-质量-阻尼系统与壳体连接.内外环与滚珠之间存在点接触,根据赫兹接触理论,滚珠与滚道接触变形在x和y方向产生的非线性恢复力具体可表示为[30]

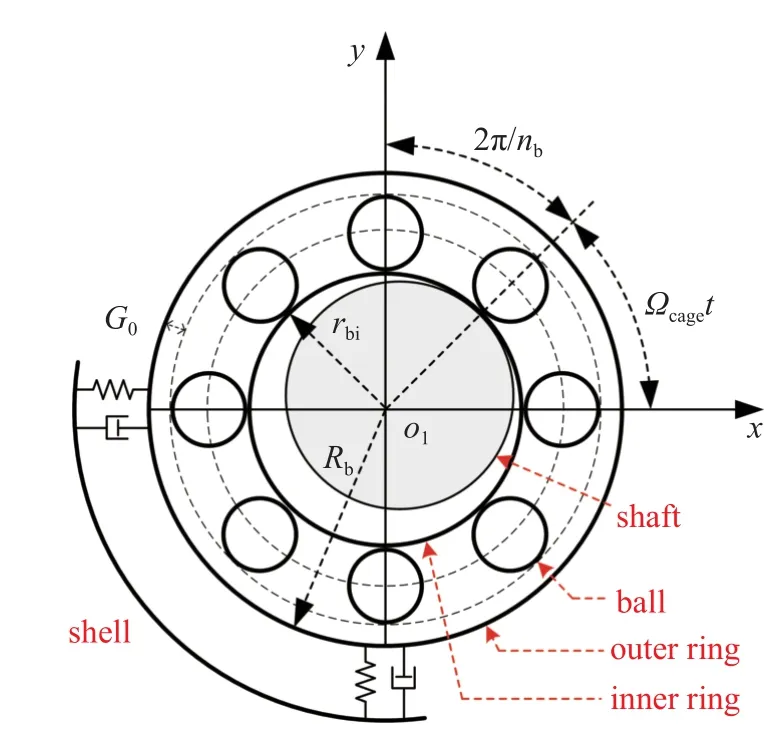
图3 非线性轴承物理模型Fig.3 Physical model of the nonlinear bearing

其中,Cb表示赫兹接触刚度系数,其大小与轴承的材料和形状有关;x,y分别为轴承内环中心在径向水平和竖直方向的位移.G0为轴承的径向间隙,H(δj)=xcosβj+ysinβj-G0为轴承的Heaviside 函数.

将总动能、势能、耗散能及激励力代入Lagrange方程中,可得到双梁系统的振动微分方程为

其中,M,C,G,K分别表示双梁系统的总质量阵、阻尼阵、陀螺阵以及刚度阵,Ω 为推进轴系的旋转角速度,Frc为RC 产生的反共振力,其原理及具体表达式见第2 小节.

其中,Ms为推进轴系和壳体质量阵,由Timoshenko梁单元质量阵组成;Me为偏心质量阵;Jdp,Jdm分别为螺旋浆和电机的直径转动惯量;Mb=mbE2nb为轴承外环质量阵,由于系统轴承参数相同,故E为单位矩阵.

其中,Ks为推进轴系和壳体的刚度阵,由Timoshenko梁单元刚度阵组成;Kc为壳体支撑弹簧刚度阵;kb为轴承外环和壳体相连弹簧的刚度.

取Rayleigh 阻尼(Rayleigh damping),故阻尼阵为

其中,α,β 均为Rayleigh 阻尼系数.

其中,Jp,Jm分别为螺旋桨和电机盘的极转动惯量.

1.2 壳体声辐射模型

为了更真实模拟AUV 在实际工况下的运动状态,将螺旋桨在空间非均匀流场中引起的噪声激励简化为施加在壳体艉部的正弦激励,可表示为

其中,Ax,Ay,ωx,ωy,αx,αy分别为在径向水平和竖直方向上激励幅值、频率和相位.

如图4 所示,为方便直观地表达壳体系统振动辐射噪声大小,采用简化球体声偶极子源推导了壳体系统的声辐射场模型,建立辐射噪声大小与壳体表面响应的数值关系[31].由于声波在传播过程中的声功率级是不变的,以此作为目标值来确定噪声的幅值.

图4 偶极子声源的声辐射模型Fig.4 Acoustic radiation of the dipole source

将偶极子源假设为一个以频率 ω 振动的刚性球体,声辐射问题可以归结为波动方程的求解,不考虑流体黏性的波动方程可表示为

其中,p为刚性球外表面的声压,k0=ω/c0为流体波长,c0为声在流体介质中的传播速度.波动方程的形式解可以写为

声压大小与振动速度的关系可以通过动量平衡方程得到.根据流体介质的速度等于壳体接触面的振动速度这一边界条件,推导出声压和速度为

其中,Ca=jωρ03/[2+2jk0a-(k0a)2],ρ0为流体介质的密度,a为刚性球的半径,则积分在刚性球表面得到的辐射声功率级为

2 RC 的工作原理及其参数设计与应用

本文将RC 简化为并联的弹簧-质量-阻尼系统,分别附加在推进轴系的径向水平和竖直方向上.如图5 所示,RC 由气缸活塞、油腔、细长导管液压油组成.工作原理的推导需要以下主要假设[32]:

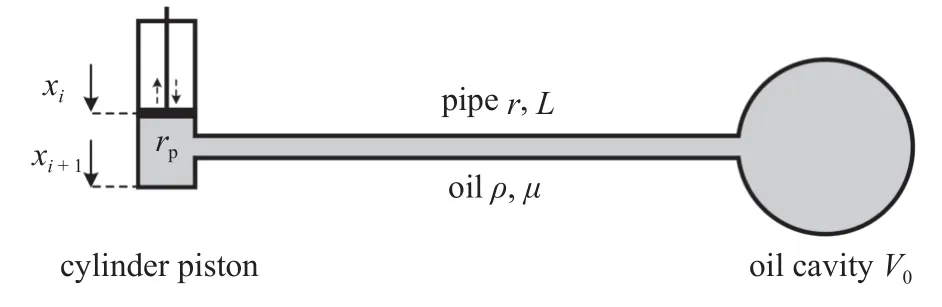
图5 RC 装置示意图Fig.5 Principle model of resonance changer

(1)气缸活塞、油腔、导管均为刚性,受力时不发生弹性变形;

(2)假设液压油在管道中的流动为层流;

(3)由于液压油大部分集中在油腔内,液压油的压缩或膨胀只发生在油腔内,气缸活塞内的液压油可忽略不计.

作用在导管内液压油上的力可以写为

其中,r为导管的横截面半径,P为作用在气缸活塞上的压力,其数值是实时变化的.

根据本节第3 个假设,油腔内液压油受到压缩产生的压力可表示为

其中,rp为活塞横截面半径,V0为油腔体积,B为液压油体积模量,(xi+1-xi)为油缸活塞相对位移.油腔内液压油对导管内液压油的作用力可表示为

液压油中的黏性阻尼特性导致管道内层流流动中具有一定的压力损失,可由本节第二个假设得到

其中,µ,ν 分别为液压油黏度及其在导管中的平均流速,L为导管长度,为气缸活塞相对速度.液压油在导管中产生的黏性阻尼力可以写为

将导管中的液压油作为受力分析对象,根据牛顿第二定律其受力状态表示为

RC 引起的反共振力由简化公式得到,上式可转化为振动方程形式,具体可表示为

其中,mr,cr,kr分别为RC 等效质量、等效阻尼和等效刚度,可将其定义为

首先求解双梁系统的动力学微分方程,扫频后得到系统的共振频率,将RC 视为单自由度系统附加在推进轴系上,其固有频率为RC 结构参数的函数,通过参数设计与优化使其固有频率与双梁系统共振频率相同,以此达到反共振的目的.

3 结果与讨论

3.1 外界激励作用下AUV 动力学响应分析

基于第2 节中建立的动力学微分方程,系统结构参数依据已公开资料和一定缩比后得到[5],其中,推进轴系、电机和螺旋桨结构参数在表1 中列出,壳体及流体介质参数在表2 中列出,表3 提供了轴承的结构参数.基于Runge-Kutta 法[33]求解系统振动微分方程.将壳体中部位置所在节点标记为C点.鉴于鱼雷等AUV 动力电机最高转速为3000 r/min,即转子偏心所能提供最大的偏心激励为50 Hz,因此选取0～50 Hz 范围进行研究.

表1 推进轴系结构参数Table 1 Model properties of the propulsion shaft

表2 壳体结构参数Table 2 Properties of the shell

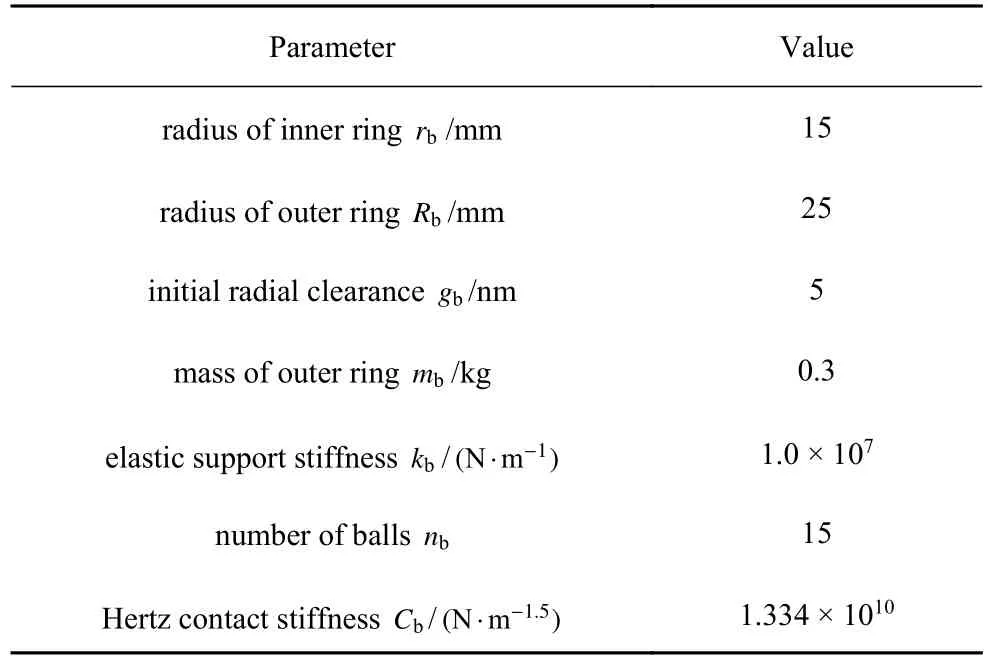
表3 滚珠球轴承结构参数Table 3 Properties of the ball bearing

图6 给出了在外界激励作用下当电机转速变化时含有非线性轴承的壳体径向竖直方向平衡状态下响应分岔图,从图中可以看出,响应曲线整体分布在径向竖直方向负区域,此现象由重力产生的位移大于振动响应位移导致.为更加直观突出共振峰,使电机在低转速下系统幅频响应保持平缓,在壳体艉部节点上施加正弦激励Fp,可以使电机在低转速下系统幅频响应保持平缓,当转速为零时,也具有一定的响应.双梁系统共有3 个共振区I,II 和III,共振频率段分别集中在P1 点(18.5 Hz)、P2 点(25.5 Hz)、P3 点(39 Hz)附近.图7 则给出了当电机转速变化时壳体径向竖直方向平衡状态下的最大振动响应,和图6 相对应,共有3 个共振峰P1,P2,P3,且3 处峰值排序为 |yC(P1)| >|yC(P3)| >|yC(P2)|,因此后面将在最大共振峰值P1 处施加共振变换器,进行减隔振研究,详细内容见3.3 小节.

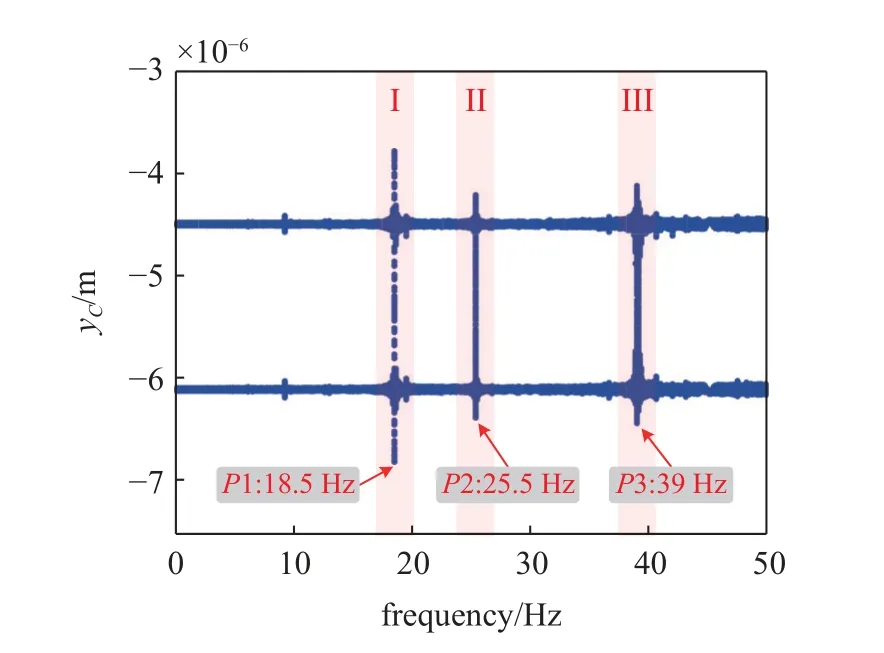
图6 外界激励下含有非线性轴承壳体响应分岔图Fig.6 Bifurcation diagram of shell under external excitation with nonlinear bearings supporting

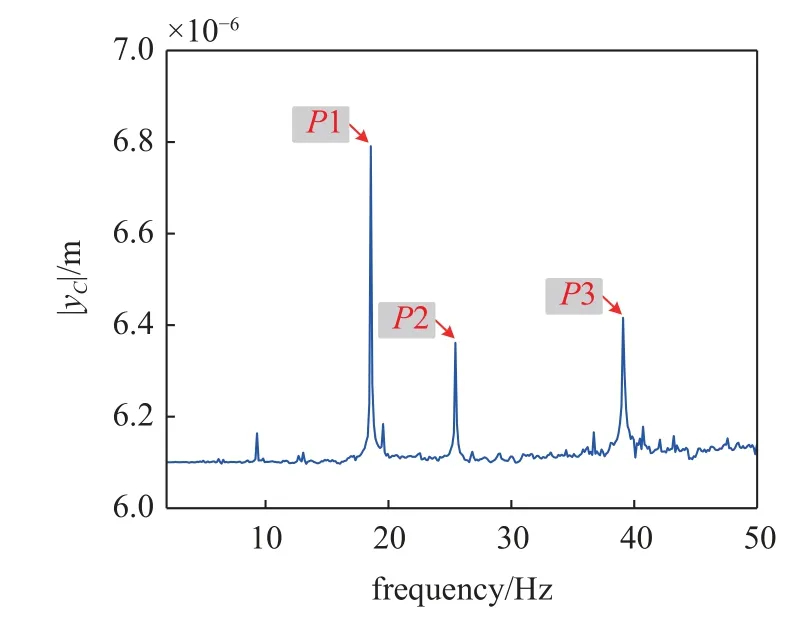
图7 外界激励下含有非线性轴承的双梁系统壳体幅频响应图Fig.7 Amplitude-frequency response under external excitation with nonlinear bearings supporting

为了深入研究共振区位置处AUV 双梁系统的动力学响应特征,选取共振峰值最大处频率点P1=18.5 Hz 和稳定频率点30 Hz 作为对比参照,其时间历程曲线、频谱、轴心轨迹和相图,如图8 和图9所示,由于在径向水平和径向竖直方向双梁系统响应结果类似,因此选取径向竖直y方向进行响应分析.在共振区域I,轴承非线性因素导致系统稳态时间历程具有多个幅值,呈现不稳定运动,如图8(a)所示.图8(b)给出了稳态历程为7～8 s 的频谱图,除了与转速同步的频率18.5 Hz 外,频谱中还观察到y方向外界激励频率45 Hz 成分以及组合频率105 Hz 成分,经研究发现在不同转速下均出现了该组合频率,此现象说明组合频率不包含转子偏心频率,实际为外界激励频率的组合 2 ωx+ωy,并且存在位移幅值关系X(ωy)>X(2ωx+ωy)>X(ω).结合图8(c)和图8(d)中的轴心轨迹与相图,系统呈现不稳定运动.共振区域II 和III 处双梁系统的动力学行为与区域I 类似,此处不再赘述.

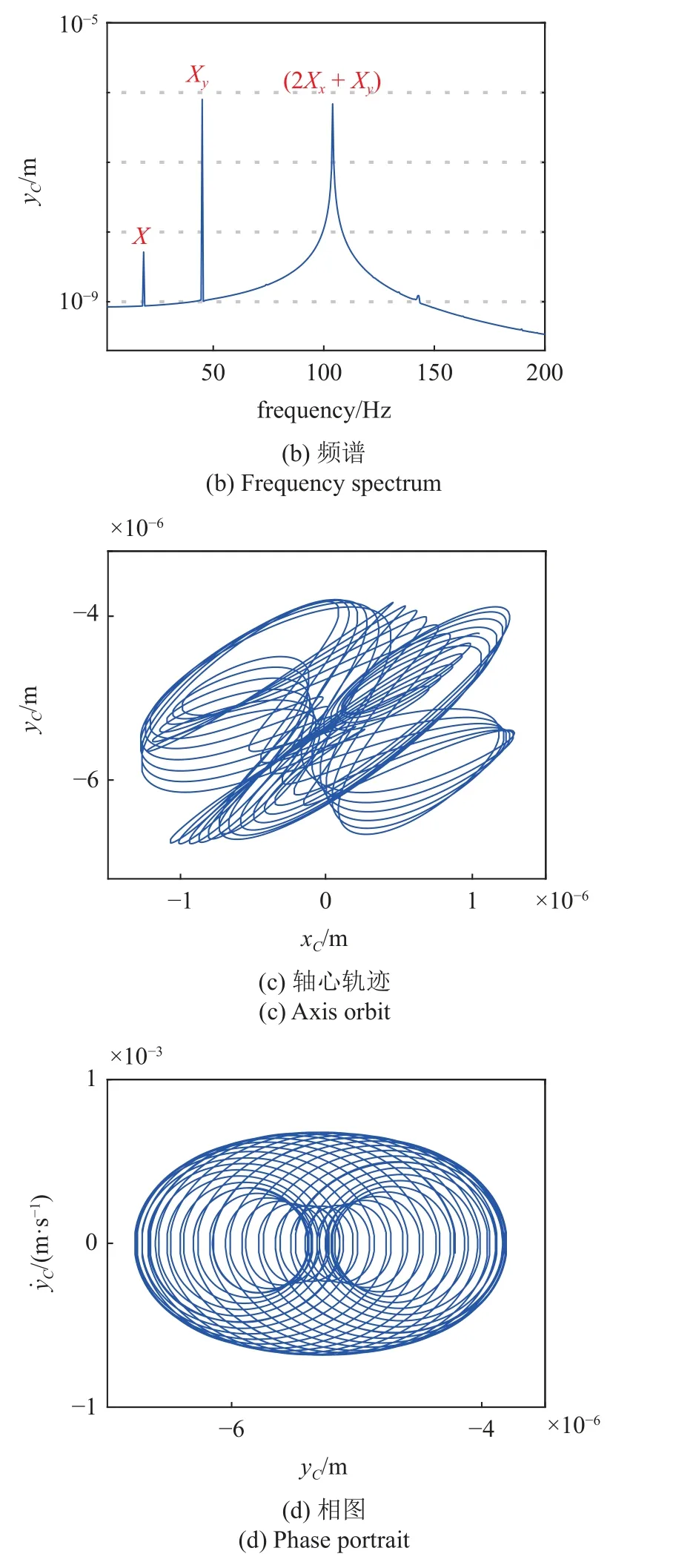
图8 P1 处壳体动力学响应Fig.8 The typical dynamic behaviors at P1 with nonlinear bearings

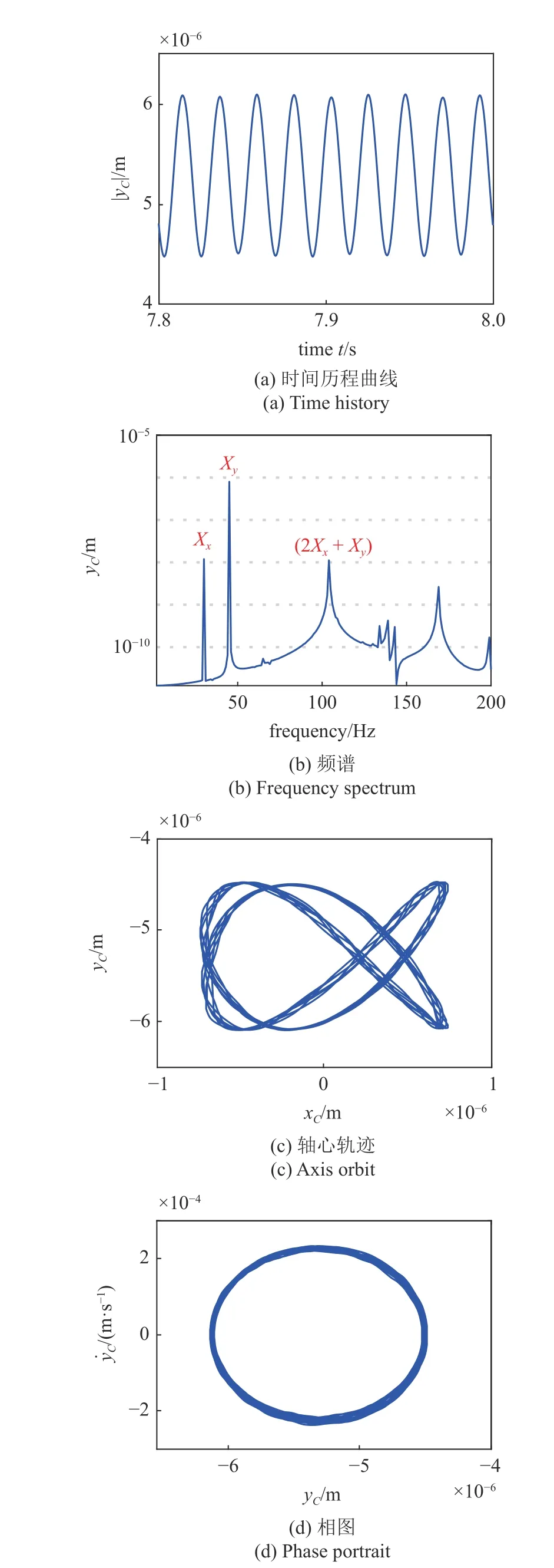
图9 30 Hz 处壳体动力学响应Fig.9 The typical dynamic behaviors at 30 Hz with nonlinear bearings

作为对比分析,选取稳定频率点 30 Hz 进行动力学分析,其结果如图9 所示.从图9(a)中可以发现,系统稳态时间历程曲线具有较少几个幅值,为周期或拟周期性运动.在图9(b)频谱中出现了转子偏心频率(与x方向外界激励频率相同)、y方向外界激励频率 ωy、组合频率 2 ωx+ωy,同时位移幅值X(ωy)最大且占主导分量,其他可忽略不计.相比图8(c),图9(c)轴心轨迹显得更加具有规律性,运动轨迹相对稳定很多.相图整体呈现规则的椭圆带状,如图9(d)所示,结合时间历程说明系统处于拟周期运动.

3.2 转子偏心激励下大推力AUV 非线性响应分析

为研究系统本身固有属性,现排除外界激励影响,仅考虑转子偏心激励.在转速一定的条件下,基于调整螺旋桨和电机尺寸来提高AUV 推力,螺旋桨半径、长度、偏心距和质量分别增加至 50 mm,30 mm,1 mm 和1.85 kg,电机半径、长度、偏心距和质量分别增加至80 mm,300 mm,0.5 mm 和47.35 kg.为避开壳体支撑弹簧共振频率落在0～50Hz,因此选取支撑刚度为4.7×107N/m使壳体支撑弹簧共振频率为所研究最大频率的2倍.

图10 给出了不同电机转速下含有非线性轴承的壳体径向竖直方向平衡状态下响应分岔图,当转速大于22 Hz 时,响应最大幅值开始出现在径向竖直方向正区域,说明此时振动响应位移大于由重力产生的位移.在低转速下系统响应较小,随着转速的升高响应逐步增大,慢慢向壳体支撑共振频率靠近并达到最大值.如图10 所示,在15～30 Hz 处系统呈现复杂运动状态,其中,双梁系统具有两个较为明显的共振区I,II,分别集中在P1 点和P2 点附近.从放大图可以看出,在P1 处响应幅值出现了较为明显的跳跃,即非连续现象,该点为分岔点,P2 处共振响应幅值达到最大,为 3.53×10-5m.

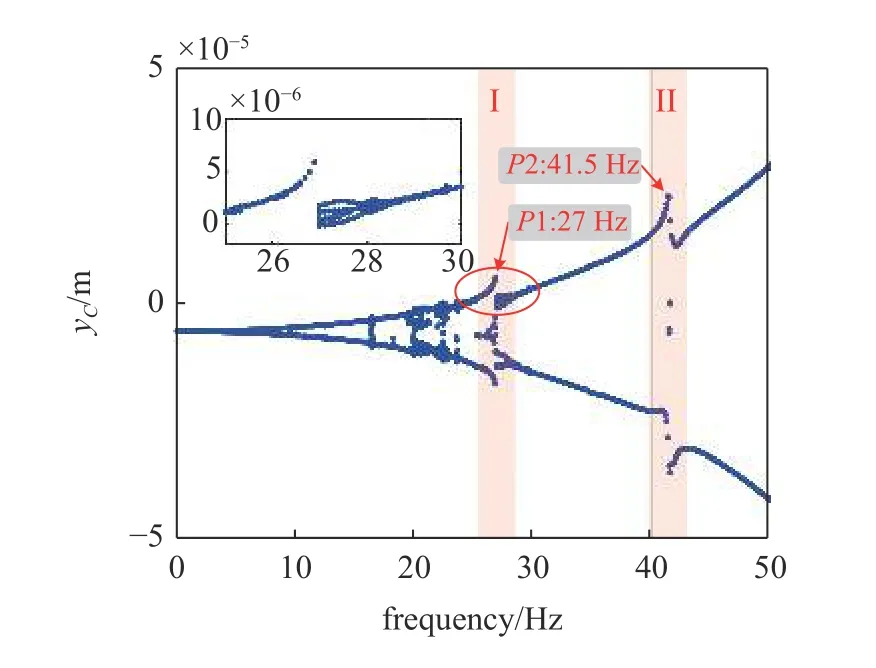
图10 不同转速下含有非线性轴承的壳体响应分岔图Fig.10 Bifurcation diagram of shell at multi-revolution speed with nonlinear bearings supporting

图11 表示转速在15～30 Hz 处壳体的轴心轨迹,该转速段壳体轴心轨迹具有多个形态,但整体上呈现圆环状.同时在x和y方向振动响应范围大致相同,说明此时转子偏心激励相比于重力占主导分量.可以观察到随着转速的不断升高,壳体轴心轨迹所示圆环边界越来越大,和实际工况相符合.

图12 表示在P1 和P2 转速(图10)下双梁系统整机的轴心轨迹,黑色线代表壳体的轴心轨迹,蓝色线代表内部推进轴系的轴心轨迹,为方便直观地观察到整机的运动情况,将推进轴系轴心轨迹缩小至原来的1/10,放入壳体轴心轨迹内部.侧向说明内部推进轴系的响应幅值要比壳体大一个数量级,这是由于壳体支撑刚度大约为推进轴系支撑刚度的5 倍导致.从图12(a)和图12(b)中可以发现,振动源与其壳体对应位置轴心轨迹边界圆环最粗,即此处振动响应幅值最大,振动向两端传递并依次递减,由于壳体艉部相比于艏部更靠近偏心桨和偏心电机,因此艉部的振动响应幅值要高1.5 倍以上,此现象与实际工况相符合.

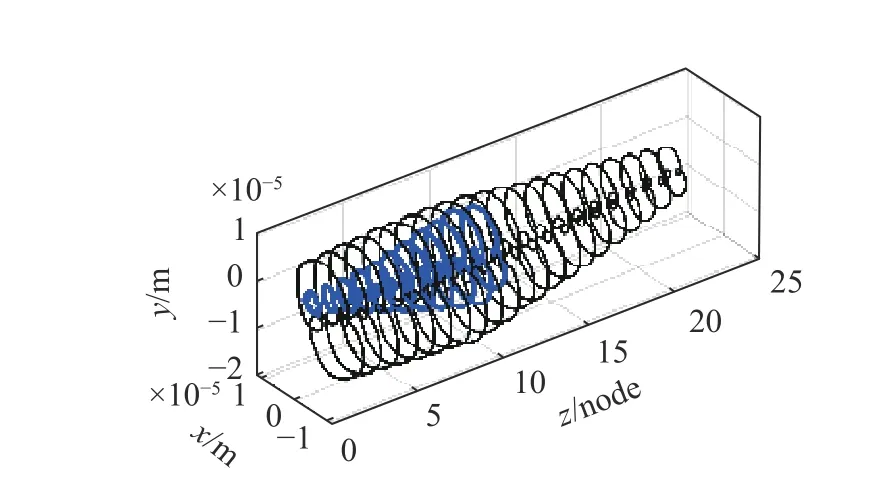
图12 在P1 点处含有非线性轴承的双梁系统轴心轨迹Fig.12 Axis orbit of double beam system at P1

选取系统分岔点P1 和共振频率点P2(图10),其时间历程曲线、频谱、轴心轨迹和相图,如图13 和图14 所示.图13(b)的频谱图中不仅包含与转速同步频率X(P1)外,还出现了2X,3X以及4X频率成分,其中,X和3X成分占主导分量,2X和4X成分可忽略不计.图14(b)的频谱图中包含X(P2),2X以及3X,其中,X和2X成分占主导分量.

图13 P1 处壳体动力学响应Fig.13 The typical dynamic behaviors of shell at P1 with nonlinear bearings

图14 P2 处壳体动力学响应Fig.14 The typical dynamic behaviors of shell at P2 with nonlinear bearings

3.3 RC 作用效果分析

RC 本质上是一个反共振装置,文献显示安装在靠近振动源位置处减振效果相对最优,因此在本文中将RC 安装于推进轴系上第7 和第8 个单元节点之间(靠近动力电机),在两节点处产生一对大小相等方向相反的作用力.基于第2 节中RC 工作原理使用流程,根据3.1 小节模型中的共振峰值及共振频率,分别选取RC 固有频率为18.5 Hz 进行结构参数设计,具体参数在表4 给出.

表4 RC 结构参数Table 4 Parameters of RC

图15 给出了在非线性轴承和线性弹簧支撑下壳体的噪声强度,即振动辐射声功率级随转速变化的关系图,国际基准声功率级为W0=1.0×10-12W.通过辐射声功率级表达式可发现壳体声功率级大小与壳体外部接触面的振动速度的平方成正比.当线性弹簧刚度取为 1.0×107N/m 时可以发现,非线性轴承支撑下的系统壳体声功率级主体趋势是沿着线性结果分布的,同时均高于线性系统噪声.在对应共振区域P1,P2 和P3 处(图6)振动辐射噪声声功率级达到峰值.

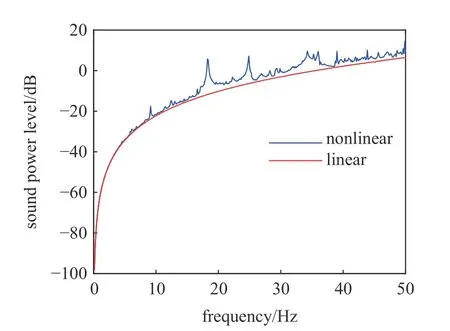
图15 非线性轴承和线性弹簧支撑的壳体声功率级Fig.15 Sound power level of shell with supporting by nonlinear bearings and linear springs

图16 表示RC 器件对含有非线性轴承支撑壳体幅频响应的影响,其中,蓝色线代表没有加入RC 的数据、红色线代表加入RC 的数据结果.可以观察到蓝色线整体位于红色线下方,说明RC 可以有效降低系统振动幅值,尤其在系统共振频率设计点处减振效果最为显著,最大共振幅值降低了52%以上.在共振频率设计点处频率没有发生偏移,但在20～30 Hz 区间内,图16 局部放大图所示,除了最大共振幅值分别降低了2%和36%之外,可观察到共振频率由22.25 Hz 和24.88 Hz 偏移到了23.75 Hz,说明RC 除了具备良好的减振效果,还可以使共振频率产生偏移,达到隔振的目的.

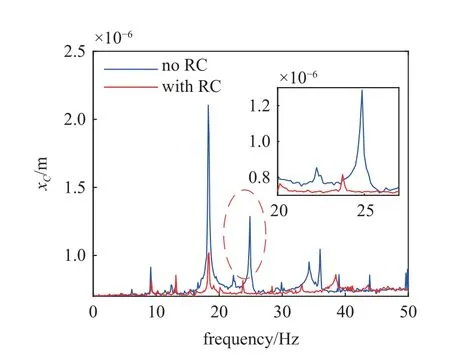
图16 RC 对含有非线性轴承支撑壳体幅频响应影响Fig.16 Amplitude-frequency response with RC and no RC

图17 表示分别在x和y方向RC 对含有非线性轴承支撑的壳体噪声抑制效果,其中,蓝色线代表初始系统声功率级大小,红色线代表加入RC 的声功率级大小.可以发现,在所研究的AUV 转速内 RC装置可以有效抑制振动辐射噪声,尤其在噪声声功率级较大15～40 Hz 处降噪效果较为显著,如图17局部放大图所示.在AUV 系统推进轴系的径向水平和竖直方向上施加具有相同参数的RC,但减振效果却不相同,对于RC 共振频率设计点(18.5 Hz),在x方向声功率级降低约9.5 dB,在y方向降低约0.4 dB,初步判定为沿径向竖直负方向的重力对RC 的减振降噪效果产生了一定的抑制作用.不过在y方向其他转速区间内噪声抑制效果格外显著,如频率段37.5～42.5 Hz 内,从最大噪声17 dB 减小至6.6 dB,降低了约61%.

图17 RC 对含有非线性轴承支撑的壳体声功率级影响Fig.17 Sound power level of shell with RC and no RC

4 结论

本文以AUV 振动噪声抑制及其隐秘性提高为研究背景,提出了一种考虑轴承非线性的AUV 振动-声学模型,并寻找RC 最佳设计参数使壳体产生的振动声辐射功率级最小,达到反共振的目的.通过Lagrange 法建立了含有浆-轴-壳的双梁模型,基于赫兹接触理论加入轴承非线性因素,根据声传播原理推出了声偶极子辐射场模型;通过 Runge-Kutta 法求解并分析了系统动力学特征,以壳体声功率级作为代价函数并根据响应分析结果,进行了RC 参数设计.基于数值研究结果可以获得以下重要结论:

(1)在不同转速下,AUV 附属的螺旋桨和动力电机作为振动源,其尺寸和装配偏心距对系统的共振频率峰值及声功率级大小影响十分显著,即其灵敏度较高,在工程中可为AUV 前期结构参数设计中提供反馈指导;

(2)通过对比非线性轴承和线性弹簧两种支撑,发现AUV 在非线性轴承支撑下壳体振动辐射声功率级主体趋势是沿着线性结果分布的,同时均高于线性弹簧支撑下的系统噪声,并且在对应共振区域达到峰值;

(3)针对AUV 双梁系统设计的RC 装置,能够大幅度降低系统共振响应幅值及振动辐射声功率级,尤其在共振频率设计点处减振降噪效果最为显著.在共振频率设计点处频率没有发生偏移,但在其他个别区间内,除了最大共振幅值降低明显之外,共振频率产生一定的偏移.

本文的理论模型揭示了AUV 动力学响应特征及参数影响规律,其研究结果可为AUV 的减振降噪优化设计提供新的改进思路,具有一定的理论指导意义.本文是在假设螺旋桨和壳体在空间非均匀流场中引起的噪声激励为正弦激励进行研究的,与AUV 实际工况下对比必然存在一定的误差.同时还发现RC 结构参数对系统影响敏感性各不相同,如果加入参数灵敏度分析将会更合理.后续,作者将在RC 作用位置优化以及结构参数选取等方面进一步开展研究工作.