一类双层薄膜结构振动能量采集器的数据驱动建模方法及应用1)

邱宏蕴 王志霞 丁 北 王 炜

(天津大学机械工程学院,天津 300350)

引言

在人们观察世界,开展生产实践,预测实践结果的过程中,建模方法发挥着至关重要的作用.传统建模方法通过对基础理论的梳理归纳以及数学演绎,得到适用于当前问题的模型.然而,该方法极度依赖先验知识,对于线性、直观问题的分析较为有效,而对于包含强非线性因素的系统则适用性有限,也因此为基于实验数据的建模方法提供了成长空间.

数据驱动建模方法,以工程实践过程中获取的物理实验数据及有限元仿真结果为基础,挖掘其中隐含的规律性,从而获取真实反映系统运动状态的动力学方程,现阶段已逐步成为国内外学者关注的热点问题.在相关领域,Frank 等[1]提出岭回归,实现了较高精度的模型预测功能.Tibshirani[2]基于最小二乘法(ordinary least square,OLS)和岭回归提出Lasso,该方法能够充分压缩模型,获得复杂度更低、解释性更好的模型.然而,Lasso 仅对于维度较低、数据量较大的问题具有较好的效果[3],且对特征值相差过大的数据模型存在过度压缩现象[4],这无疑降低了其广泛应用于实际场景的可能性.为了解决此类问题,Zou 等[5]提出弹性网络(elasticnet,EN),该方法补充了Lasso 在高线性相关数据处理方面的不足,具有更好的模型压缩效果.此后,诸多学者[6-8]建立了基于实验数据的模型辨识方法,以识别动力系统的输入、输出和噪声等信号在系统模型中的表现形式.上述方法主要识别非线性振动方程中的具体参数,并不能直接建立系统动力学模型,因此仍属于参数识别的范畴.此后,Donoho[9]利用压缩感知中关于近似最优子空间的研究,证明了Banach 空间理论在稀疏识别中应用的可行性.Wang 等[10]采用稀疏识别和压缩感知理论构建非线性动力学系统,以实现对故障信号的预测和诊断,但是由于模型复杂度高以及频繁出现的模型压缩过度等问题[11],仍不能直接建立完整的动力学模型.直至2016 年,Brunton 等[12]提出了稀疏非线性动力系统辨识算法(sparse identification of nonlinear dynamical systems,SINDy),实现了从实验数据到非线性控制方程的过渡,并且极大地简化了模型复杂度,提高了算法鲁棒性.

此后,Rudy 等[13]基于SINDy 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics,PDE-FIND),江昊等[14]、刘吉悦[15]通过对PDE-FIND 的研究,证明其对于强非线性偏微分方程的识别也具有较好精度,弥补了SINDy 难以识别非线性偏微分方程的不足,进一步提升了方法的实用性.聂滋森等[16]将稀疏正则化方法应用于悬臂梁损伤识别中,仅使用少量数据即可识别损伤的位置和强度,实现了正则化方法在小训练集问题上的实际应用.与另一种广泛使用的数据驱动方法动态模式分解[17](dynamic mode decomposition,DMD)相比,SINDy 无需假设基本形式,可直接通过实验或者仿真数据获取系统的非线性控制方程,因此实现了模型复杂性与计算精度之间的平衡,并且在机械和生物等诸多领域具备应用价值[18-19].

然而,工程实践中的数字信号通常会受到噪声干扰,即使微小的噪声信号,都可能导致误差的急剧放大,进而在一定程度上影响以SINDy 为代表的数据驱动建模算法的分析精度[20].因此,学者们将滤波模块与数据驱动方法进行前后叠加,形成了提升建模方法可靠性的噪声数据处理方法.如Brunton 采用的全变分正则化(total-variation regularization,TVR)[21]处理,以及Zou 等[22]提出的稀疏主成分分析(SPCA),在降维的同时也达到了降噪的目的.与前后叠加的噪声处理方法类似,这些方法依次进行数据滤波与数据驱动,先后达到降噪与建模的目的,其降噪效果虽然显著,却未必能达到最佳的系统识别精度.因此,处理好数据滤波与数据驱动之间的关系,实现二者的有机结合,而并非简单叠加,才是减小噪声影响,提高识别精度的可能途径,值得进一步研究.

另一方面,在数据处理过程中,当非线性函数库构成的状态矩阵特征值差异较大,各分量间线性相关程度较高时,矩阵将呈现病态矩阵的性质.SINDy在处理此类病态矩阵时,容易表现出模型压缩过度[20]和多解[23]等问题,即所谓奇异性问题.面对奇异性问题时,SINDy 可能表现出较低的鲁棒性,并影响其识别结果的准确性[24-25].因此,解决奇异性问题对于提升以SINDy 为代表的数据驱动方法的实用价值具有重要的现实意义.

作为应用,本文讨论的电磁式薄膜振动能量采集器(electromagnetic vibration energy harvester,EMH),由环境振动作为激励源,带动薄膜上的永磁体振子做低频振动,并导致相应的线圈内部的磁通量发生变化,产生感生电动势.为深入研究该EMH的复杂振动特性,需要构建精确的动力学模型.然而,对于振幅较大的薄膜结构而言,强几何非线性以及阻尼因素的影响较为明显,这为直接运用力学理论建模增加了难度.在包含强非线性因素的控制方程中,线性项与非线性项系数数量级差距很大,状态矩阵的构造方式更加复杂,不仅容易产生模型压缩过度[20]和多解[23]等问题,对数据驱动算法的鲁棒性以及建模精度也提出了更高要求.因此,尝试数据驱动方法与非线性理论相结合的建模方式,更适合精确构建此类薄膜结构EMH 数学模型,进而开展复杂的振动行为分析.

综上所述,针对数据驱动方法难以处理的强噪声、强奇异性问题,本文将SINDy 算法进行相应的改进,提出了增强型稀疏非线性系统辨识算法(enhansed sparse identification of nonlinear dynamical systems,ESINDy).结合传统非线性理论研究方法,通过研究一类双薄膜式双稳态振动能量采集器的动力学特性,对ESINDy 算法精度及稀疏效果进行分析和验证,以期为数据驱动方法的实际应用提供参考.

1 识别算法

1.1 SINDy 算法及数据滤波算法

由于传统数据驱动建模方法存在耗时长、模型复杂等问题,Brunton 等[12]提出了SINDy 方法,并在其中加入了TV-R 数据滤波算法.该方法是一种利用实验数据进行数据驱动建模的方法,主要原理是将给定的一系列非线性函数组成基函数库,并将基函数库构建的状态矩阵与TV-R 算法构造的导数矩阵形成线性残差优化问题,求解该优化问题得到各个基函数分量的系数,最终获得较为精确的控制方程.

(1)数据滤波算法

总变分正则化(TV-R)是最常用的数据滤波手段之一,但求解较为复杂.Gong[26]提出的曲率滤波(curvature filters,CF)在TV-R 的基础上,使用更简结的算法达到更好的滤波效果.

传统正则化方法的正则化项能量会随着优化进程的进行而逐渐降低,而正则化项作为优化主体,能量的降低会导致优化效果变差,曲率滤波使用已知的曲率来优化其对应的正则项,从而达到更好的优化效果.对一维含噪信号x(t),曲率可表示为

其中,Ix和Ixx分别表示x(t)对t的1 阶、2 阶导数.对一维含噪信号,曲率表示的正则化项可表示为

其中,λ为正则化参数.在dt的步长下,曲率优化更新过程可表示为

正则化方法依赖正则化参数的选择[27],然而在实际问题研究过程中,通常需要先进行数据滤波,随后使用滤波后的数据进行SINDy 数据驱动.这就导致正则化参数不能随着数据驱动问题的变化而自动选取,限制了SINDy 的工程场景应用[28].

(2)SINDy 算法

假设振动系统的方程可以表示为如下形式

其中,x(t)为系统在t时刻的状态,f(x(t))为系统控制方程.矩阵 Θ 为由给定非线性函数构成的基函数库

根据基函数库,构造状态矩阵A

假定控制方程f(x(t))可由基函数库中的部分项构成,Ξ 为基函数库中各成分系数构成的矩阵,则振动系统方程可表示为

因此,在已知导数矩阵与状态矩阵A的前提下,对振动系统方程的识别问题可转化为对的识别问题.该问题可通过最小二乘法(OLS)解决,目标函数Target可以表示为均方误差形式

化简式(9),最小二乘法解可表示为

Lasso 法[2]通过在最小二乘法目标函数后增加L1 正则化项的方法,达到稀疏效果.稀疏方法可以简化复杂的数学模型,得到项数较少的简单模型来表征系统的动力学特性,并综合考虑模型压缩程度和模型精确性之间的矛盾.Lasso 法的求解目标可表示为

求解驻点,并将式(10)代入

SINDy 以Lasso 解作为循环主体函数,将式(12)不断迭代,使得均值误差处在一定容许范围内,从而求得稀疏矩阵的局部最优解,进而完成控制方程的重建.

虽然SINDy 具有不依赖先验知识,能够直接从数据中建立控制方程的算法优势,但由于Lasso 方法本身对特征值差距较大的系数识别效果较差[4],这就使得SINDy 面对病态矩阵时也产生了类似的诸如模型压缩过度等奇异性问题[20,23],需要进一步改进.

1.2 ESINDy 算法

具体而言,关于SINDy 存在受噪声数据影响显著和难以识别病态矩阵等不足,主要表现为: 一方面,SINDy 虽包括基础的抗噪功能,但面对强噪声就需要引入额外的降噪手段,这其中数据处理和识别过程会放大噪声,需要加入额外的数据滤波模块减小噪声影响.现有数据驱动方法针对噪声的处理通常是在数据驱动前对数据信号进行降噪预处理.这种方法虽然简单便捷,但数据滤波与识别作为相对独立的两个过程被割裂开来,因此从算法的整体性和完整性角度考虑,还存在提升空间[28].另一方面,SINDy 通过构造时间序列矩阵,从而将控制方程的识别问题转化为线性优化问题,并使用Lasso 法作为循环主体函数对优化问题进行分析.时间序列矩阵构造方法的局限性会加大其内部低阶成分与高阶成分间线性相关程度和特征值差异,导致以Lasso作为循环函数体的SINDy 在处理相关数据时存在明显的局限性.

有鉴于此,本节从数据滤波模块和稀疏识别循环函数体两个方向入手,提出改进型SINDy 分析方法(ESINDy),如图1 所示.该方法将曲率滤波正则化参数与识别结果的稀疏性(sparsity,SP)进行关联,实现数据滤波与数据驱动的有机结合,以改善数据滤波效果;同时,使用弹性网络(EN)代替Lasso 作为循环主体函数,使其在面对线性较强、特征值差异较大的数据时有更好的处理效果;最后,借助帕累托前沿分析(Pareto front analysis)[29]确定最小均值误差,从而自动筛选最优解.

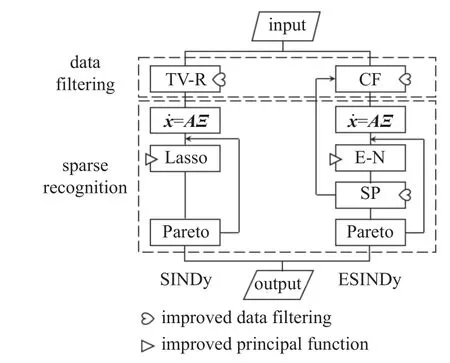
图1 SINDy 分析模式与ESINDy 分析模式对比Fig.1 Comparison between SINDy and ESINDy

(1)数据驱动部分

使用L1 正则化项的Lasso 能够实现良好的稀疏效果,但对病态数据的识别能力存在显著不足,导致SINDy 在处理此类数据时出现精度降低、压缩过度等问题.使用L2 正则化项的岭回归,虽然无法得到精简模型,却能在处理上述数据时具有更好的鲁棒能力,实现较高精度的识别.EN 同时使用L1 和L2 正则化项,巧妙地结合了L1 的稀疏能力与L2 的鲁棒能力,因而具有更好的识别效果.EN 的等价优化问题为

经推导可知闭式解可表示为

(2)数据滤波部分

TV-R 和曲率滤波等正则化滤波算法具有处理频带宽、降噪效果好等优点,然而正则化参数通常使用经验选择,极大地限制了其通用性[27].在所有可能解中,稀疏性意味着能够使用较少的项描述模型的本质,从而制定较为精简快速的控制方案.因此,筛选适合的正则化参数,使得识别结果稀疏度最大,并使用该参数执行曲率滤波,即可识别到更为稀疏的模型.

ESINDy 算法流程如表1 所示,其中:X为待处理数据,λ1,λ2为正则化参数,iter为循环次数,Sp为通过L1 与L2 范数间差异定义的稀疏度,表达式为

表1 ESINDy 算法流程Table 1 ESINDy algorithm

上述方法不仅解决了正则化参数筛选困难的问题,还将曲率滤波与SINDy 有机结合,赋予了正则化参数新的物理意义,从而提高数据滤波效果,间接提高了稀疏识别的准确性.接下来将针对Rösler 系统进行研究,以验证ESINDy 方法处理奇异性问题的有效性.

1.3 Rösler 系统识别

Rösler 系统作为混沌系统,识别结果的微小差异会显著反映在系统中,并且标准Rösler 系统的计算集具有一定的奇异性,这无疑对SINDy 算法的鲁棒性和奇异问题的识别能力提出了新的挑战.

数学上常使用条件数判定矩阵奇异及病态程度,矩阵奇异性越强,条件数越大.Rösler 系统数值解状态矩阵条件数为 3.227×103,具有一定病态矩阵的性质.分别使用SINDy 与ESINDy 识别该系统,x分量识别结果如表2 所示,关键参数识别结果如表3 所示.

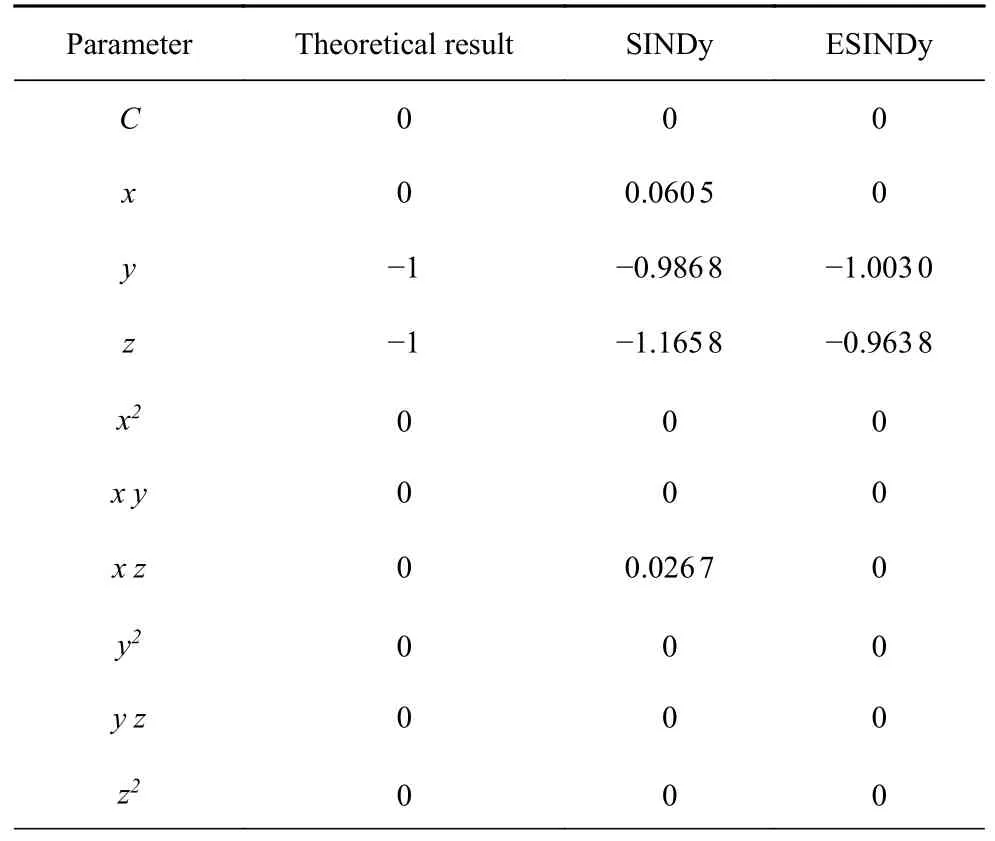
表2 x 分量识别结果Table 2 x component identification result

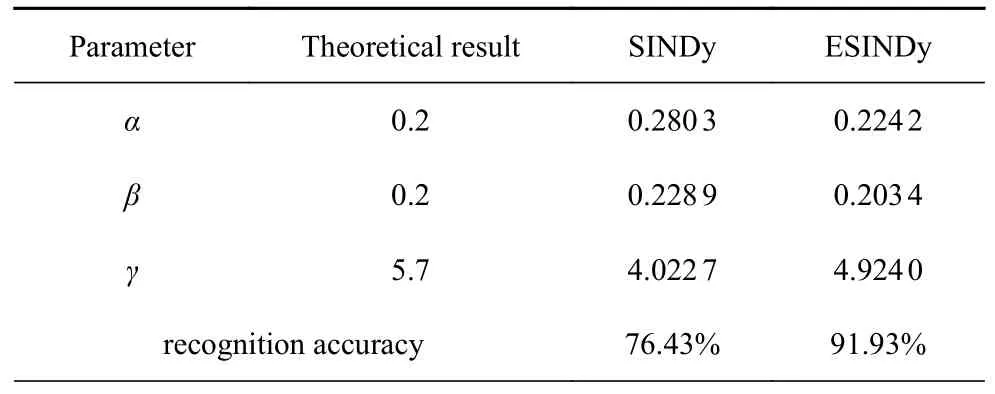
表3 部分参数识别结果Table 3 Partial parameter identification results

由表3 可知,ESINDy 较SINDy 具有更高的识别精度.就识别结果中稀疏项的正确率而言,ESINDy(8 项,100%)较SINDy (6 项,75%)更高,具有更好的稀疏效果.

如图2 所示,使用两种方法分别重构系统并计算x分量数值解,ESINDy (90.71%)的准确率远高于SINDy (44.59%),证明ESINDy 在面对奇异问题时拥有比SINDy 更优越的性能.

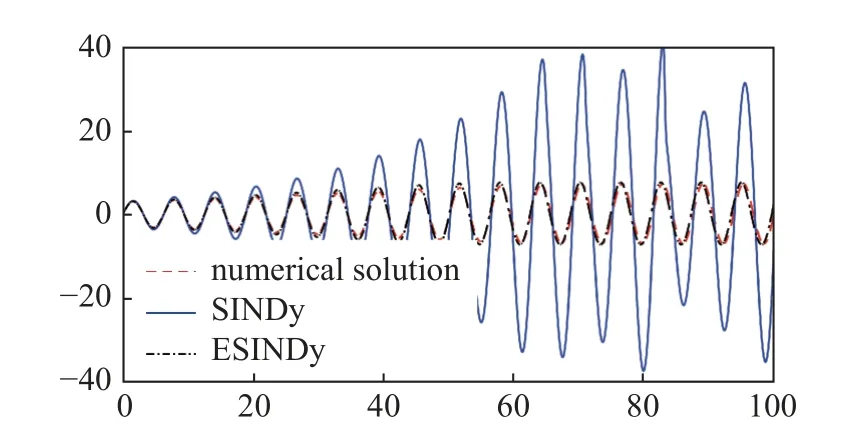
图2 重建系统x 分量数值解Fig.2 Numerical solution of x component of reconstruction system

2 实验模型

2.1 非线性结构设计

选用一类双薄膜式双稳态振动系统作为算法的实际应用范例,结构示意图如图3 所示.该结构主要由薄膜、中间质量体、外壳和外部磁铁组成,其中:质量体携带磁铁通过切割镶嵌在外壳中的线圈产生电流,两端通过磁铁固定在薄膜上,并与外部磁铁相吸引;上下端盖可通过旋转改变外部磁铁与薄膜上磁铁间距,从而改变磁力大小.实验与仿真结果都表明,对常见的单层薄膜结构而言,双薄膜的设计可以有效地避免由于质量体周向旋转而产生的无关振型.

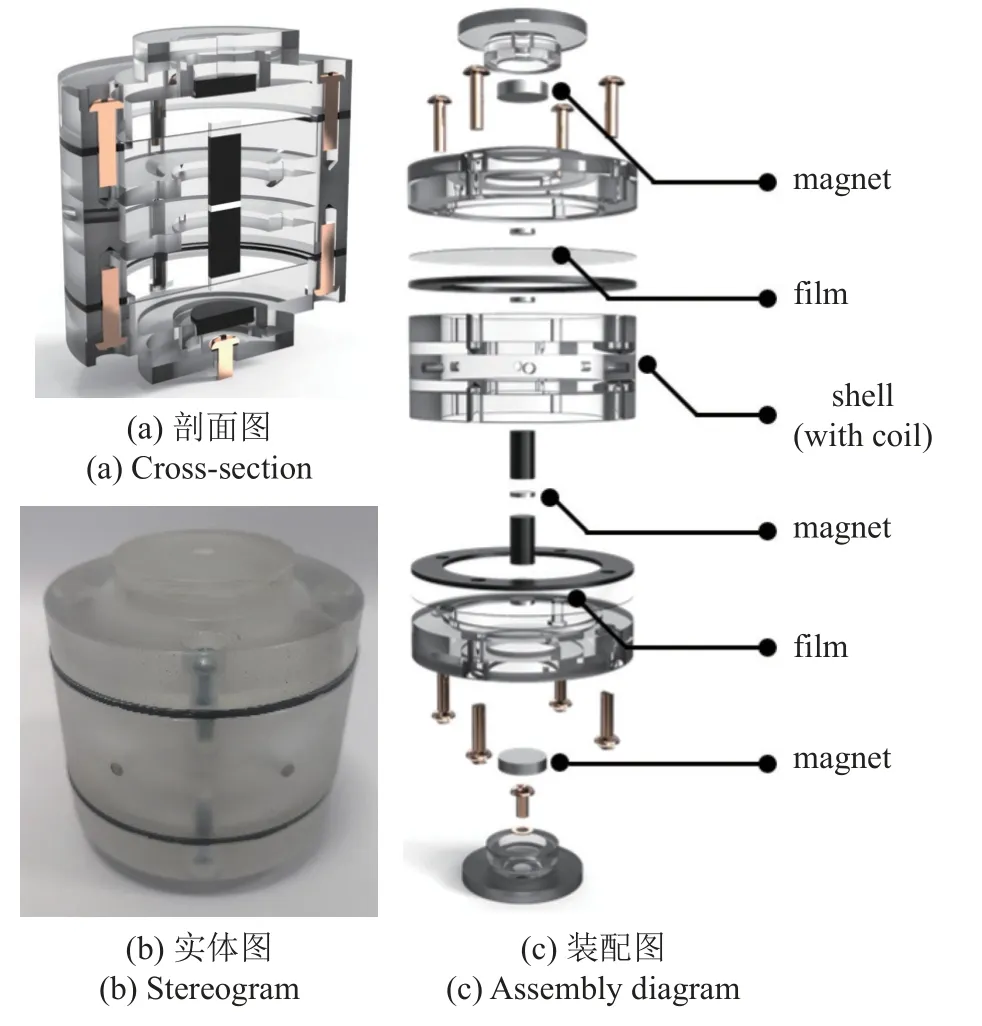
图3 双薄膜式双稳态振动系统结构Fig.3 Double-film-type bistable vibration system

质量体的振动微分方程可表示为

其中,c()表示阻尼项,k(x)表示弹性项,e(x)表示磁力项,h(t)表示激励项.

2.2 非线性项分析

对强非线性耦合系统而言,非线性项会极大影响系统的非线性响应及动力学行为[30],因此识别非线性项是识别系统方程的重中之重.系统控制方程中非线性成分主要由弹力、磁力提供,使用板壳理论分析弹力项.挠度方程可表示为

其中,ω 为挠度,q(ρ,θ)为极坐标表示下的载荷,D为抗弯刚度.实验模型可简化为中间受集中载荷环形模型,积分求解式(18),最大挠度可表示为

其中,P为作用于中间区域的集中载荷,R为圆环半径,孔径比 ξ=r/R.该模型最大挠度为

通过对比式(19)和式(20),发现 ωm与 ωp成正比.因此,可由中间孔的尺寸确定挠度改变的程度ωm=G(ξ)ωp,定义无量纲偏移系数

薄膜恢复力与挠度的关系为

由于薄膜为大变形,力-变关系实际满足如下关系

当 ω <ωL时,式(23)所述关系可以认为是小变形.3 次拟合关系近似斜率与线性关系斜率应满足下述条件

挠度小于半径的1% 可以认为是小变形,即ωL=0.01R,则恢复力与薄膜变形关系可表示为

振子质量为M,故弹力项可表示为

对于磁力项,由磁偶极子理论[31-32],一对圆形磁铁间磁力Fe(l)可表示为

其中,C为与永磁体剩余磁通密度、空间磁导率、永磁体体积有关的常数,a和b为与永磁体半径和厚度有关的常数.EMH 具有两对距离相同的磁铁,假设在振子位移为x时,磁铁间磁力可表示为

其中,l为两端磁铁间距离.磁力项e(x)通过泰勒展开可表示为3 次多项式形式

其中,M为振子质量,c1和c3为未知定常数.磁铁力矩关系可表示为

其中,f(x)为不包含关于x的1 次和3 次项的未知函数,a1和a3为待拟合系数且有如下关系

通过测量并拟合单对磁铁力-距关系的a1和a3并代入式(31),即可获得c1和c3,并由式(29)得到磁力项.

2.3 参数测量及仿真

在对EMH 系统进行识别前,需要先对其动力学建模后的结果进行实验与仿真,以验证动力学建模结果的正确性,便于与数据驱动建模结果进行比较.

针对磁力项,使用COMSOL Multiphysics 5.X进行仿真计算,并搭建如图4(a)所示实验系统,测量磁力与磁铁间距离的关系.

图4 磁力及弹力参数测量装置 (1.测力计,2.手轮,3.磁铁,4.EMH)Fig.4 Magnetic force and elastic force parameters measuring device(1.dynamometer,2.rocker,3.magnet,4.EMH)

实验与理论、仿真结果比对结果如图5 所示.实验中两磁铁距离在 5 ∼10 mm 间变化,该区域实验和仿真数据较为接近,因此对距离l>5 mm 的仿真数据进行3 次多项式拟合

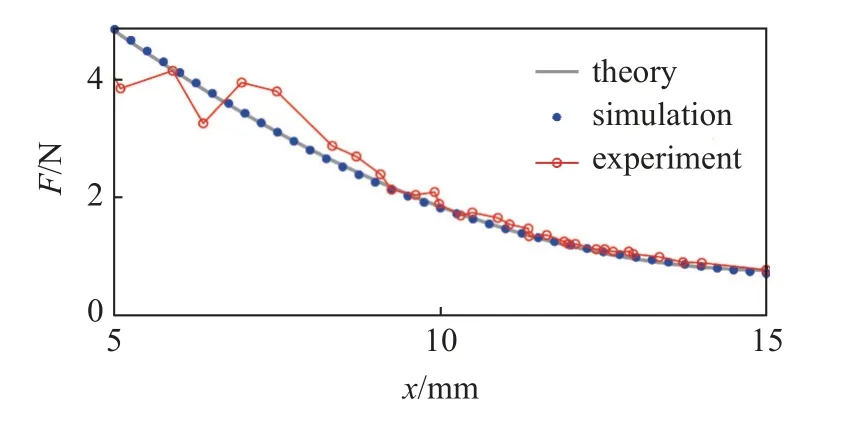
图5 磁力的实验、仿真与理论结果Fig.5 Experimental,simulation and theoretical results of magnetic force

将式(32)代入式(29),磁力项可表示为

针对弹力项,使用Ansys Workbench 进行有限元仿真,几何参数与仿真参数见表4,仿真模型为周边夹支边界条件的圆环模型.

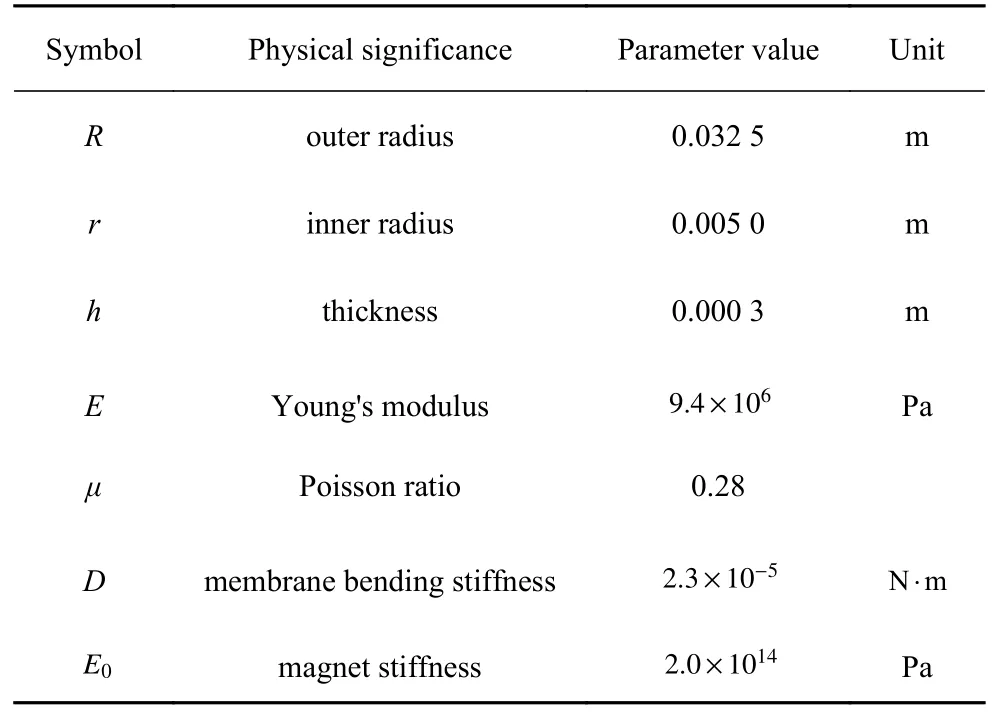
表4 Ansys 仿真采用的模型参数Table 4 Model parameters used in Ansys simulation

EMH 可视为孔径比 ξ=2:13 的圆环,根据式(25),恢复力与薄膜中心点位移应满足

此处考虑内部气体压强影响,则导致力-变关系存在一定偏移

其中,假设内部空气压强比大气压高1%,则中心偏移量b≈2 mm,此时力-变关系可表示为

搭建如图4(b)所示的实验系统,测量恢复力与中央磁铁位移的关系,并将测试结果与理论、仿真结果比对,如图6 所示.首先,无偏移理论与仿真数据吻合,这说明从理论角度对于薄膜结构弹力的分析较为准确;其次,在考虑中心偏移的情况下,实验测试数据与式(36)的力-变形关系基本吻合,也证明了偏移假设的必要性.因此,后续分析以式(36)的弹力关系作为实际表达式.

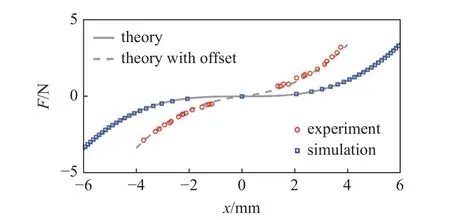
图6 恢复力实验、仿真与理论结果Fig.6 Results of experiment,simulation and theory of resilience

3 实验

搭建如图7 所示振动测量实验系统,使用位移传感器测量振子振幅,加速度计测量样机外壳加速度.测量得到的振幅和加速度数据信噪比约为31 dB,为混杂了一定强度随机噪声的采集信号.使用振幅和加速度数据构造状态矩阵,状态矩阵条件数为 1.056 3×1013,表现出病态矩阵的性质.

图7 振动实验测试系统Fig.7 Vibration experimental system

分别使用SINDy,ESINDy 两种分析方法进行数据驱动建模,两种方法的识别结果和理论结果的对比如表5 所示.

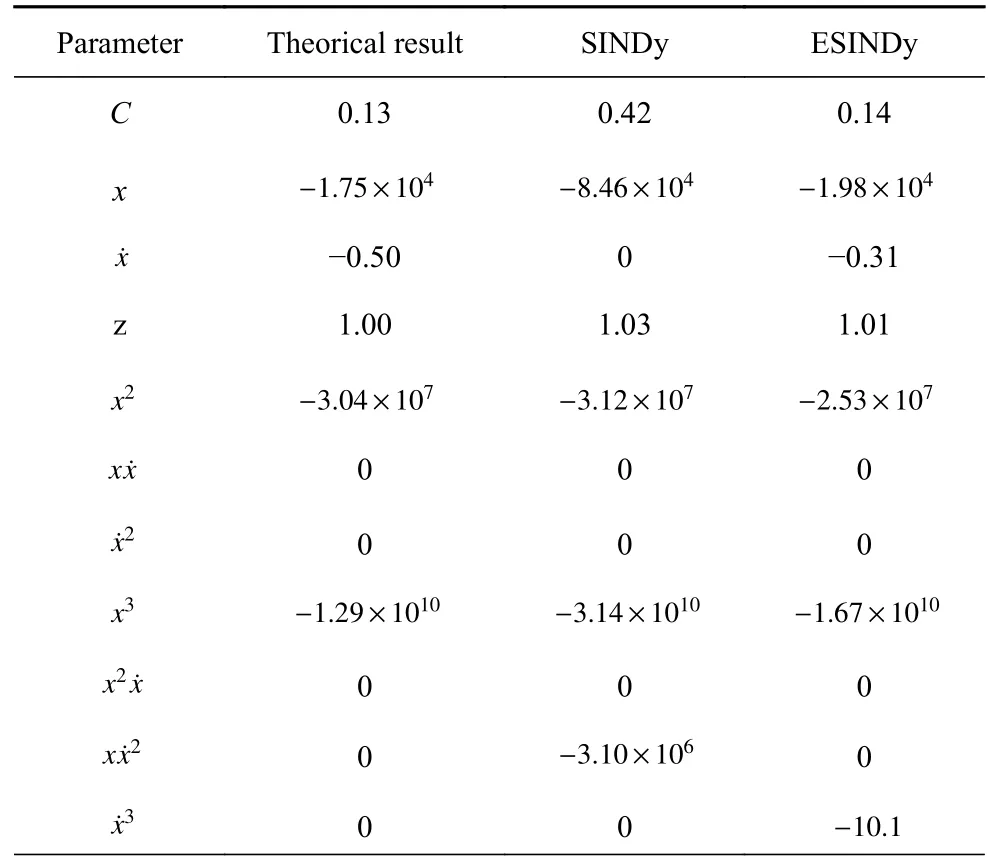
表5 理论和识别结果对比Table 5 Comparison between theory and identification results

相比较传统理论手段建模,数据驱动方法具有精度更高,能够识别到难以识别的阻尼和非线性项等优势;相比较单一使用数据驱动方法建模,理论与数据驱动相结合的方法能够预先估计可能含有的项及部分项的系数,具有更高的精度和更宽的应用场景.

比较两种数据驱动方法,从识别结果来看,ESINDy的识别准确率(83.07%)相较于SINDy (62.48%)有显著提高.就稀疏项的识别准确率而言,ESINDy 正确识别稀疏项数(4 项)与SINDy (4 项)相仿,ESINDy 错误识别稀疏项数(0 项)低于SINDy(1 项),表明SINDy 面对病态矩阵确实存在过度压缩现象,而ESINDy 则没有此类问题.

从系统重构效果来看,SINDy 对系数筛选的错误导致相图中重要信息的丢失.如图8 所示,ESINDy重构相图表现出与真实相图类似的马鞍形状,且鞍点与稳定点的位置几乎相同,而SINDy 重构相图仅表现出一定的非线性特点.

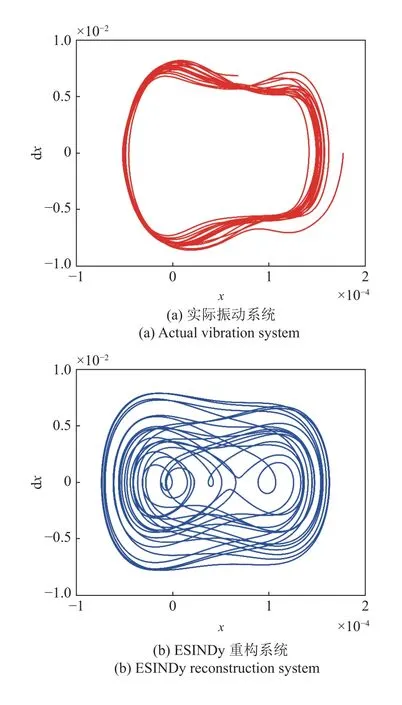
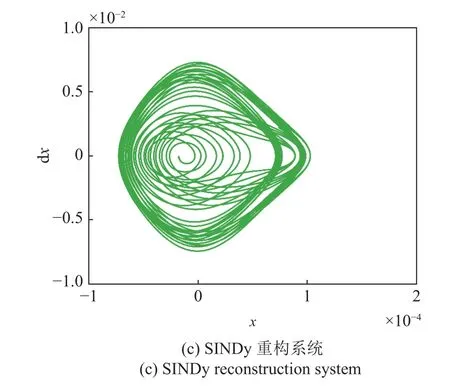
图8 振动系统真实相图与SINDy,ESINDy 重构系统相图Fig.8 Real phase diagram of vibration system,SINDy and ESINDy reconstruction system

4 结论

本文针对传统SINDy 方法难以处理强噪声数据和奇异系统的缺点进行改进,提出改进型ESINDy算法.改进主要集中在将曲率滤波与SINDy 进行结合,从而提供更适合的正则化参数,以获得更好的降噪效果;使用ElasticNet 作为SINDy 的循环主函数体,从而大大增强了SINDy 对奇异系统的处理能力.使用ESINDy 算法识别Rösler 模型和EMH 模型,研究得出如下结论.

(1)通过对Rösler 系统的分析,证明相较于SINDy,ESINDy 在稀疏项筛选精度和有效项识别精度上均有显著改善,精度提升约15%～20%,说明改进方法有效提高了针对奇异问题的分析能力与分析精度.

(2)通过对EMH 系统的分析,证明数据驱动方法具备重建控制方程的能力,其中: 基于对重构系统的数值计算与分析,系统的动力学特点得以更加深入而准确地呈现,即ESINDy 能够准确识别出EMH 系统的鞍点、稳定点、周期、振幅等隐含信息,且避免了诸如过度压缩等问题,表现出比SINDy更优越的性能.

(3)稀疏辨识算法既可以识别理论分析方法无法计算的参数,又可以完善系统的控制方程.随着研究对象日益复杂,利用稀疏辨识算法结合理论方法对物理模型进行预测的手段具备潜在优势.

在后续研究中,将发挥ESINDy 方法的优势,对于EMH 的复杂振动问题进行进一步的深入分析.