离心式气流分级机不同湍流模型流场模拟结果分析与对比研究
2023-11-15孙国刚
刘 波,孙国刚
(1.中国五环工程有限公司,湖北 武汉 430223;2.中国石油大学(北京),北京 102299)
离心式气流分级机是目前应用最广泛的粉体分级设备,原理是利用强制涡流中粉体颗粒受到的离心力与空气曳力的不同进行分选,但是分级机内部结构复杂,很难通过实验分析其内部流场的特点。分级机内部流场的分布特点决定了粉体颗粒的运动方式,因此提高分级机分级性能,开发高效离心式气流分级机,必须对分级机内部流场进行准确有效地分析。计算流体动力学(简称CFD)技术是分析分级机内部流场的一条有效途径。旋流分离中的单相湍流数值模拟大多采用标准k-ε模型、RNGk-ε模型、雷诺应力模型(简称RSM)。各种模型都有其优缺点及适用性,为流场分析选择准确、合适的湍流模型,准确且有效地预测内部流场具有至关重要的作用。目前,对离心式气流分级机内部流场模拟如何选择湍流模型研究鲜有报道。北京化工大学的研究团队[1-4]和西南科技大学的研究团队[5-8]一般采用RNGk-ε模型或RSM进行研究,对局部叶片之间的流场分析也可采用标准k-ε模型[9]。本文采用标准k-ε模型、RNGk-ε模型、RSM这3种湍流模型对广泛用于催化剂细粉分级及S-Zorb废吸附剂分级[10]中的LHF型[11-12]分级机进行模拟计算,分析其内部流场的速度分布特性,并通过实验利用五孔球探针[13]测量分级机内部流场速度,验证模拟的准确性。
1 控制方程和湍流模型
1.1 控制方程
假设分级机内流场是等温、不可压过程,分级机内的气相流动可以用不可压流体的连续性方程和动量守恒方程(2)来描述。连续性方程为:
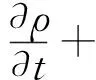
(1)
动量守恒方程为:
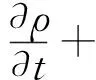
(2)
其中,

1.2 湍流模型
1.2.1标准k-ε模型
标准k-ε模型是由Launder和Spalding于1972年提出的双方程湍流模型,用于求解湍流动能k方程:
(3)
以及湍流耗散率ε方程:
(4)
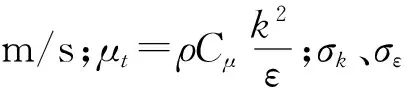
1.2.2RNGk-ε模型
RNGk-ε模型在标准k-ε模型的基础上修正湍流黏度,考虑了平均流动中旋转及旋流流动的情况,因此可以更好地预测强旋流和弯曲程度较大的流动。湍流动能k方程为:
GK-ρε
(5)
湍流耗散率ε方程为:
(6)
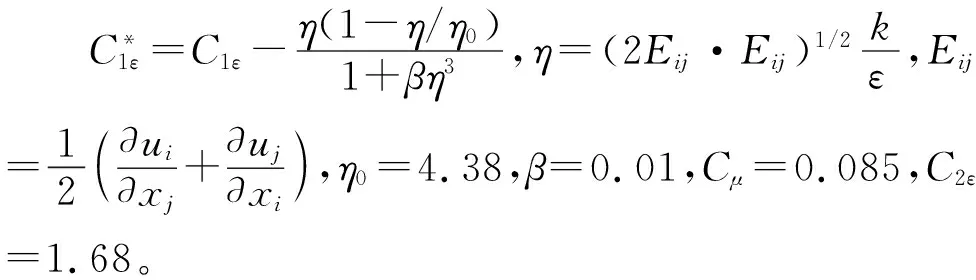
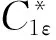
1.2.3雷诺应力模型
RSM是根据时均化法则构建雷诺应力的输运方程,对输运方程中产生的未知项按梯度模拟的概念模拟,并模拟与压力脉动有关的关联项,从而构成封闭方程组。在三维模拟中需要求解包括控制流体运动的时均方程、湍流动能k方程、湍动能耗散率ε方程和雷诺应力方程在内的7个方程。该模型摒弃了湍流各向同性的假设,在强旋流和大曲度流动模拟中表现较好[15]。
湍流动能k方程为:
(7)
湍流耗散率ε方程为
(8)
雷诺应力方程为:
(9)
其中,
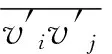
2 计算前处理
2.1 网格划分
模型选取实验用LHF-300型分级机,分级机内径为312 mm,直筒段高为450 mm,转轮叶片数为40,径向安装,转轮外圆直径为160 mm,转轮以雷诺应力方程模型y轴为旋转轴,风筛入口结构为多切向入口结构。通过ANSYS软件的前处理软件DM建立模型,然后导入Meshing划分网格,分级机三维模型及网格划分见图1。网格划分均采用四面体网格,并对转轮区域进行加密处理,网格总数约为7×105,网格最大畸形值为0.87。
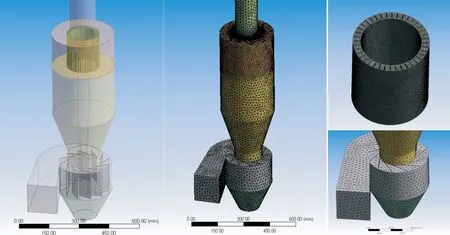
图1 分级机三维模型及网格划分
2.2 边界条件
设置流体介质为空气,密度为常数。采用SIMPLE算法求解速度与压力耦合,计算时分别采用标准k-ε模型、RNGk-ε模型、RSM这3种模型。考虑到分级机内部流场是非稳态的,同时为了提高模拟的计算精度,采用非稳态求解方法。分级机内部为强旋流动,具有各向异性,压力梯度采用PRESTO!格式。离散方程其他项均采用二阶迎风格式计算以提高计算精度,近壁区域采用壁面函数法处理。
将分级机分为静止区域和转动区域2个部分,区域之间设置为交界面。将转动区域与静止区域之间的耦合设置为滑移网格,同时确定转动区域的转速及旋转方向。根据实验工况,转速为3 528 r/min,入口气量为250 m3/h,设置速度进口边界条件为v=3.1 m/s,出口设置为压力出口。模拟计算中,迭代的时间步长为0.000 5 s,时间步数为2 000,计算的物理时间为1 s,时间步长内最大迭代次数为50。对进出口压降进行检测,发现气流流动时间超过0.6 s后压降趋于稳定,表明分级机内部流场在0.6 s后形成了稳定的强旋流场。
3 流场模拟结果与分析
3.1 方向和截面的定义
分级机内流场是一个复杂的三维强旋流场,切向速度vt、轴向速度vz、径向速度vr,这3个速度分量的正方向定义见图2。为了准确比较3种湍流模型对分级机内部流场的计算结果,分别考察3个代表性截面上切向、径向与轴向3个速度分量,并与实验值对比(见图3)。截面Ⅰ是分级轮中间的截面,截面上切向速度占主导,切向速度决定颗粒的切割粒径。由于实验测量无法在分级轮内部测量,因此从分级轮外缘开始取点。截面Ⅱ是筒体中部的截面,是颗粒分散及滞留区域,从中心轴开始取点。截面Ⅲ是锥体段中部的截面,靠近入口区域。
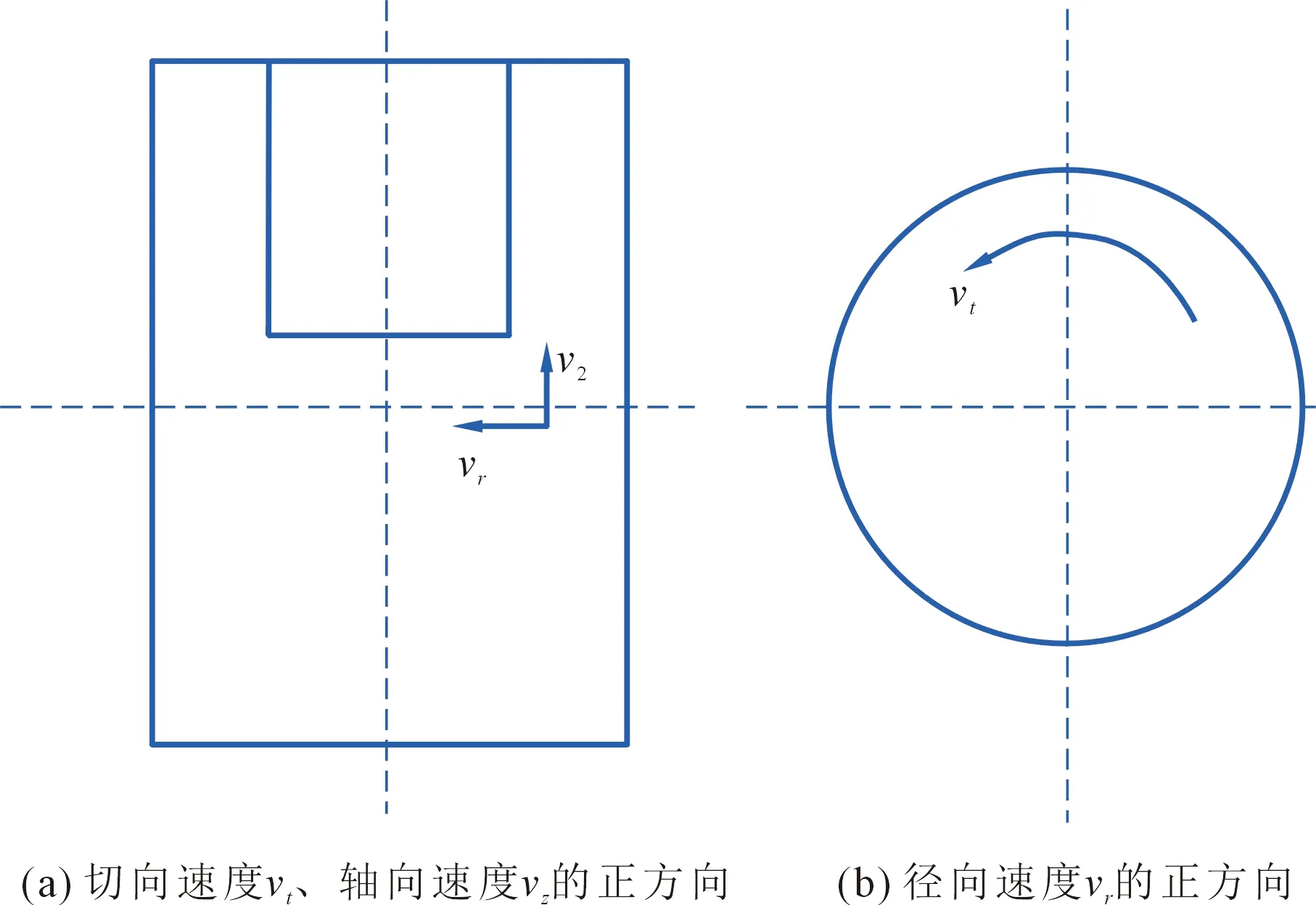
图2 分级机内流场
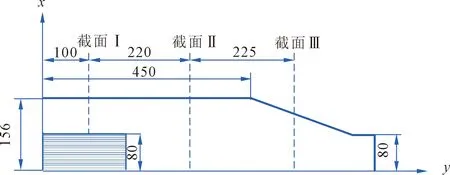
图3 分级机内部结构及截面划分
3.2 3个方向的速度对比
3.2.1切向速度对比
在分级机内,切向速度占主导地位,由它带动颗粒进行高速旋转运动,颗粒在离心力的作用下甩向外壁而被分离出来。图4所示为不同湍流模型计算得到的切向速度与实验实测值的对比。可以看出,3个截面上标准k-ε模型的计算结果均与实测值差别很大,标准k-ε模型计算的切向速度分布过于平缓,特别是在锥体段截面Ⅲ上,与实测值相比,无法定性预测切向速度的走向。原因是采用了湍流局部各向同性的假设,难以描述实际中各向异性的强旋流[16]。RNGk-ε模型计算的结果能较好地定性预测切向速度的分布趋势,但是与实测值有一定的偏差,特别是在叶轮附近,截面I模拟计算得到的切向速度均大于约为2 m/s的实测值,RNGk-ε模型在计算切向速度时,预测值会有一定的夸大。3个截面上RSM计算结果的数值和趋势均与实测值接近,可以很好地预测分级机内的切向速度。

图4 3个截面上切向速度沿径向的分布
3.2.2轴向速度对比
轴向速度分布较复杂,一般可将轴向速度分为外侧下行流和内侧上行流2个区域,原因是风机的抽吸使气流向上运动,到达转轮附近时,转轮的高速转动产生强烈的“风扇排风”效应,一部分气流经过顶壁被排向边壁,到达边壁后沿壁面向下运动形成下行流。图5为不同湍流模型计算得到的轴向速度值和实验实测值的对比。可以看出,3个截面上RNGk-ε模型预测轴向速度的计算结果与实测值相比,速度分布的趋势与定量分析相差都很大。标准k-ε模型的计算结果仅在截面Ⅰ上与实测值接近,在截面Ⅱ、Ⅲ上不能很好地预测轴向速度的分布。在转轮附近的截面Ⅰ上,RSM可以很好地预测上行流和下行流的分界点,在锥体段截面Ⅲ上,轴向速度先增大,然后在边壁面减小,与实测值的基本趋势一致。从上行流转变为下行流是一种变换曲度较大的流动,这也验证了该模型摒弃湍流各向同性的假设[17],在大曲度流动模拟中表现较好的结论。
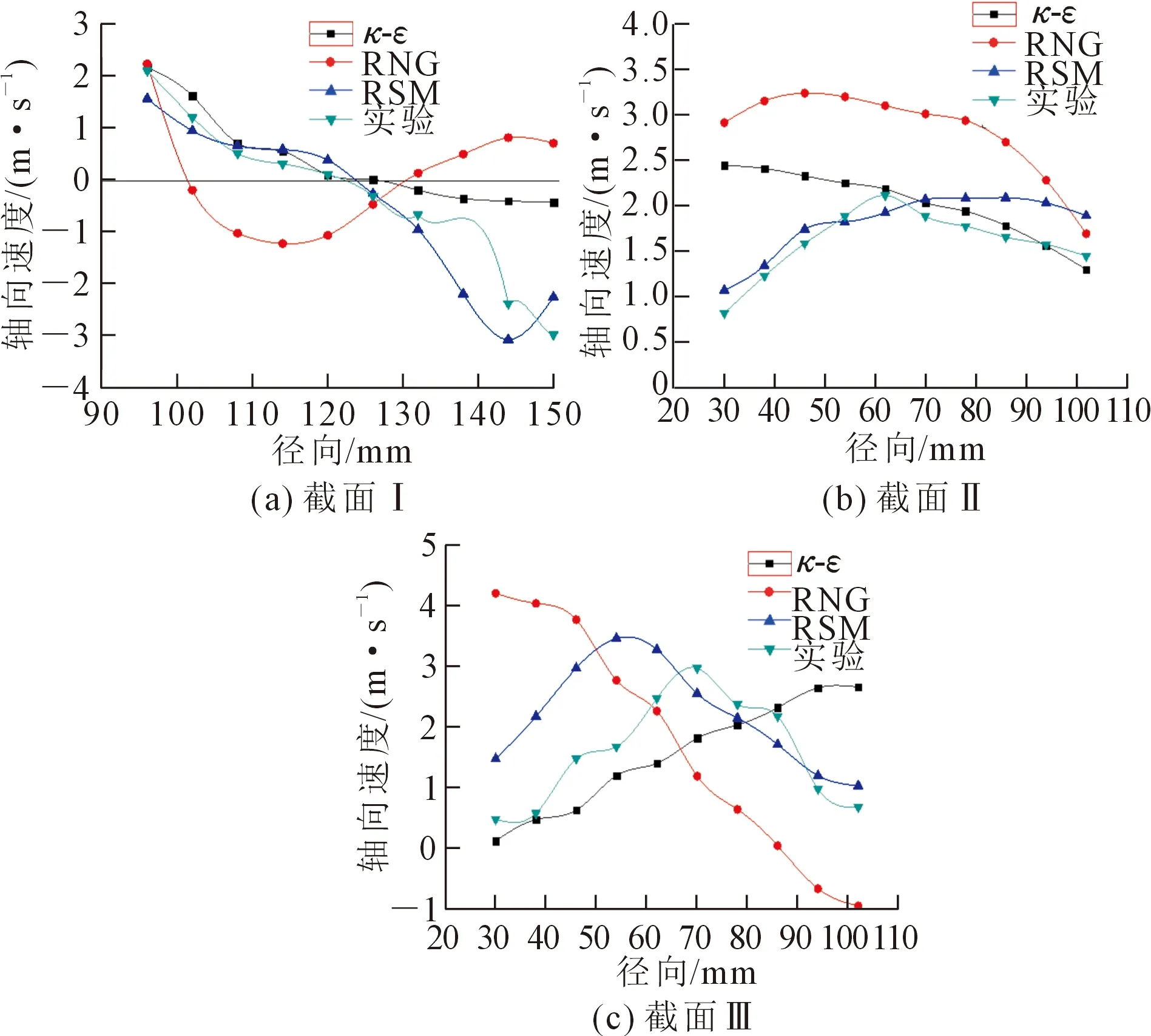
图5 3个截面上轴向速度沿径向的分布
3.2.3径向速度对比
径向速度vr大部分沿半径方向由壁面指向分级机中心,只有在二次环流处有小部分的向外流动。图6为不同湍流模型计算得到的径向速度值和实验实测值的对比。可以看出,在截面Ⅰ、Ⅱ上,RNGk-ε模型预测径向速度的计算结果与实测值相比,速度分布的趋势与定量分析相差都很大,RNGk-ε模型预测内部流场切向速度时可靠性较好,但是轴向和径向速度分布与实测值相去甚远。原因如下:虽然RNGk-ε模型是在标准k-ε模型的基础上,通过修正湍动黏度来适应更高的应变率及弯曲度、更大的湍流流动,但是仍然对充分发展的湍流更有效。标准k-ε模型的计算结果仅在截面Ⅰ、Ⅱ上与实测值接近,但是径向速度分布过于平缓,不能很好地预测径向速度的走势。在截面Ⅰ和截面Ⅱ上,RSM模型计算结果的数值及趋势均与实测值接近,可以较好地预测径向速度分布,但是在截面Ⅲ上,3种模型都无法很好地预测径向速度分布,实测值的径向速度波动较大,原因可能是锥底截面处的径向速度分布较复杂,此处为入口区上部,流动不稳定,变化较大,因此难以预测此处的径向速度。
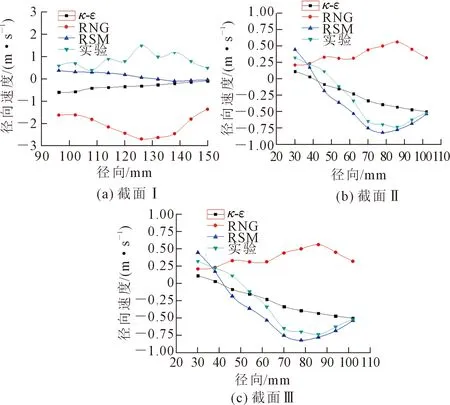
图6 3个截面上径向速度沿径向的分布
4 结语
(1)通过采用标准k-ε模型、RNGk-ε模型、RSM这3种湍流模型,对广泛用于催化剂细粉分级中的LHF型分级机进行模拟计算,发现标准k-ε模型计算的结果在3个方向上的速度均难以预测趋势,RNGk-ε模型预测切向速度时表现良好,但是预测轴向和径向速度时,与实测值差距较大,这2个模型不适用于离心式气流分级机内的强旋流流动。
(2)RSM预测的3个截面上切向与轴向速度均与实测值较接近,在截面Ⅰ、Ⅱ上可以较稳定地预测径向速度,离心式气流分级机流场特性研究时可以利用RSM模型进行模拟计算,为深入研究分级机内部的流动趋势、开发高效的离心式气流分级机提供了较可靠的依据。
