基于BELLHOP 声线模型的水声信道特性研究∗

代 伟

（91388部队 湛江 524022）

1 引言

随着陆地资源持续不断的开发，导致了资源的短缺，人们纷纷把视线投向了海洋，并且由于世界各国海军的建设和发展的需要，也要求对海洋有进一步的认识。水声信号是目前人们所掌握的主要的水下信息传播载体，在水下目标探测［1］、水声定位［2］、水声对抗［3］、水声通信［4］等领域发挥着重要的作用。水声信号在海洋中传播，海洋是水声信号传播的信道，由于海洋中噪声干扰严重［5］，多途［6］和混响［7］等也严重影响着信号的传输，可以将海洋信道看作是一个随着时间、空间、频率变化的滤波器。海洋信道对水声信号的传播起着关键的作用，因此研究水声信道的特性具有重要的意义。

对于水声信道特性的研究，很多科研机构做了大量而有意义的工作，这些富有意义的工作有力的推进了水声领域科研的进步，促进了水声探测、水声定位、水声导航等领域的研究。文献［8］基于射线理论模型，建立了两种常用的水声信道模型：相干多途信道模型和时变信道模型，模型在某种程度上反映了水声信道的主要特点。文献［9］提出的时变多径水声信道模型基本上实现了对海洋水声信道的模拟，在一定程度上反映了海洋介质的物理特性；对Rayleigh 衰落模型的仿真，反映了海洋介质的不均匀性以及信号在水声信道中传输的时变特性。文献［10］简要分析了水声信道的传播特性，主要针对水声信道强烈的多径效应的特点，研究了浅海水声多途信道的物理模型，并通过BELLHOP 射线传播模型实现了声场环境模拟以及水声信道的建模。文献［10］采用BELLHOP模型对水下信道进行仿真，并研究了对目标声源的探测方法和阵列最佳布放方法与声线的关系。但水声信道受声速剖面、海水深度、海底掠射角、水声信号传输距离等多种因素的影响，并没有文献对这些综合因数对水声信道的影响给予研究。

本文基于BELLHOP 声线模型，通过计算机仿真的方法研究了水声信道各种因素对水声信号传输的影响，研究了声线的传播损失和时延随传播距离的变化关系，海底反射损失和海底掠射角的关系，声线传播损失和水声信号传播深度的关系以及和水声信号传播距离的关系，并得出了一些有益的结论。

2 声线模型的基本原理［12～13］

在经典声线声学的研究范畴内，对声场的描述是由声线来传递声能量的，从声源发出的声线经过一定的路径传播到达接收点，接收点的声场是由所有到达接收点的声线叠加形成的。由于声线都有一定的传播路程，因而不同的声线到达接收点时相应的都有不同的到达时间和不同的到达相位。每条声线可以看作是一个能量管道，每根声线管携带的能量守恒，因此，声线强度由声线管的截面变化确定。在声线声学的范畴内有两个基本的方程：一个是用于确定声线传播规律的程函（Eikonal）方程，另一个是用于确定单根声线强度的方程。

声线声学的这两个基本方程可以由波动方程在一定条件下近似得到。简谐振动过程的波动方程为

设波函数ψ为

将式（2）代入式（1），并分离实部与虚部，则有：

在式（3）中，如果略去第二项，即当满足：

时，则得到S(x，y，z)的方程为

式（6）即为声线声学的第一个基本方程——程函方程（Eikonal），由它可以确定声线的走向。声线的方向定义为等相面S(x，y，z)=const的法线，于是声线的方向矢量γ(α，β，γ)为

可由微分几何中关于曲线S(x，y，z)=const的法线方向余弦得出：

由式（4），并注意到

∇∙(A2∇S)=2A∇A∙∇S+A2∇2S，

可得到声线声学的第二个基本方程，即强度方程：

如果考虑到声线强度I为

则由式（8）给出：

即声线强度矢量满足管量场条件diν(I)=0，由式（9）所定义的声线强度其数值正比于波函数ψ的幅度A的平方，而其方向即为声线的方向。

由上面的讨论可知，由声线基本方程式（6）及式（10）所确定的波函数ψ为

ψ=A(x，y，z)eik0S(x，y，z)

是在条件式（5）得到满足时波动方程的近似解。

以上理论便是BELLHOP 声线模型的理论基础。根据上述波动方程的理论公式，在一定边界条件和约束条件下，运用计算机编程计算便可得到特定环境条件下的定解。这就是本文研究的理论基础。

3 仿真计算结果与分析

水声信道可以看作是一个随时间、空间、频率变化的滤波器，它受水声信道波导的多种条件的影响。本论文仿真计算时设定发射信号声波频率为200Hz，海深100m，声源深度为50m，接收换能器深度为50m，海洋传播距离为1000m，海水声速剖面的声速变化范围为1523m/s 至1541m/s，海水密度为1022kg/m3，海水中横波吸收系数为69.2912dB/wavelength 至69.4261dB/wavelength，海底沉积层厚度为20m，沉积层中声速度为2000m/s，沉积层密度为1810 kg/m3，沉积层中横波吸收系数为0.5dB/wavelength，仿真中计算10条声线的传播路径。

图1 为仿真计算出的10 条不同声线的传播路径。海面反射声的落点位置由近及远依次排列，可以看出10条声线每条都会经过海面反射，图中有8个反射点，另有两个反射点的位置出现在1000m以外的海面上，前8 个海面反射点距离声源的水平距离依次分别为179.1m、226.9m、303.6m、440.3m、570.3m、707.4m、752.1m、928.4m。并且从图中可以明显看出海面反射点和海底反射点距离声源的距离越近声线传播路径越趋近于直线传播，而随着海面反射点和海底反射点的位置距离声源越来越远，声线呈现不同程度的弯曲，距离越远弯曲程度越大。

图2 为每条声线的传播损失随传播距离的变化关系以及每条声线的时延随传播距离的变化关系。由图中可以明显地看出距离声源越近的地方，声线的传播损失越大，最大值的地方达到接近100dB 的值，随着传播距离的增加，声线的传播损失逐渐变小，在最远距离处，声线的传播损失约为60dB。声线的时延随着传播距离的增长而线性增长，距离声源越远的地方，声线的传播时延越长。10 条声线的时延和传播损失与传播距离的变化关系的规律一致，有很多地方交叠在一起，总体看来，在距离声源100m 的地方，声线的时延约为0.07s，在距离声源1000m的地方，声线的总体时延大约为0.66s。

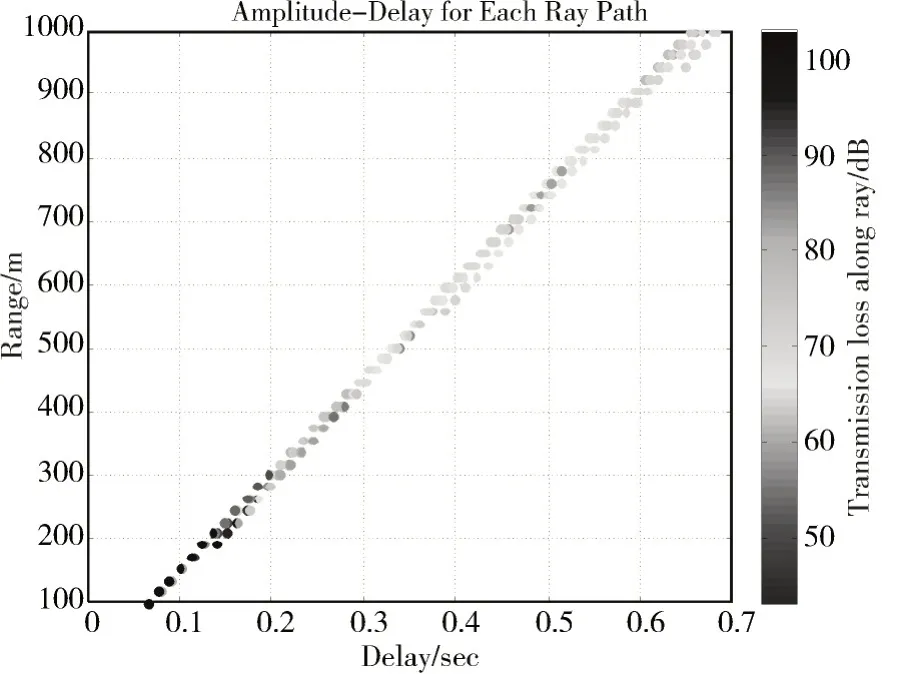
图2 每条声线的传播损失与时延

图3 为海底反射损失与海底掠射角的关系。由图中可以看出随着海底掠射角的增加，海底反射损失值也在不断的增加，在掠射角为38°的值之前，海底反射损失随着掠射角的增加大致成线性增长的趋势，并且海底反射损失的增长非常缓慢，从0dB 增长到0.4dB 左右，在这一角度以后，海底反射损失的值急剧增加，成抛物线形快速增长，在海底掠射角的值达到90°时，反射损失的值达到最大，为7.9dB 左右。由此看来，海底掠射角的变化对声线的海底反射损失的影响很大，大的掠射角会增大海底的反射损失，因此在实际的水声信号的传输过程中，应当尽量保证信号经过海底反射时的掠射角尽可能的小，以减小海底的反射损失，从而保证信号可以传输得更远，以增大声纳的探测作用距离。

图3 海底反射损失与海底掠射角的关系

图4 为声线的传播损失与深度的变化关系。可以看出在海深小于100m 的水深中，声线的传播损失小于60dB。本论文中计算时设置的声源深度为50m，从图中可以看出在声源位置处，声线的传播损失为0dB，而随着声线的传播偏离声源的深度位置时，声线的传播损失成逐渐增大的趋势，在水深从50m逐渐减小到0m也即逐渐接近海面的过程中，声线的传播损失逐渐增大，最大传播损失接近58dB，而在水深从50m逐渐增大到100m的过程中，声线的传播损失也逐渐的增大，在海底的位置处，声线的传播损失达到59dB。

图4 声线传播损失与深度的变化关系

图5 为声线传播损失随传播距离的变化关系。由图中可以看出随着水声信号传播距离的增加，信号的传播损失值大致呈现逐渐增大的趋势。在距离声源很近的水平距离上，水声信号的传播损失大致为32dB，随着距离的增加，声线的传播损失逐渐加大，从图中可以看到，在距离声源840m左右的位置处，声线传播损失的值达到71.32dB。由此可以得出如果要使声音信号能够有更大的传播距离，需要增大发射信号的功率，但发射功率的增加会使得水中的空化噪声增大，影响信号接收机的工作，因此需要处理好这两者之间的关系。

图5 声线传播损失与传播距离的关系

4 结语

本文以BELLHOP 声线模型为理论依据，初步研究了水声信道的一些特性。首先详细的讲述了BELLHOP 声线理论模型的基本原理，并推导了声线方程的基本公式；计算了水声信道中10 条声线的传播路径，研究发现一次海面或海底反射点距离声源的距离越近声线传播路径越趋近于直线传播，而随着一次海面或海底反射点的位置距离声源越来越远，声线出现不同程度的弯曲，距离越远弯曲程度越大；距离声源越近的地方，声线的传播损失越大，随着传播距离的增加，声线的传播损失逐渐变小，声线的时延随着传播距离的增长成线性增长，距离声源越远的地方，声线的传播时延越长；海底反射损失随着掠射角的增加先线性缓慢增长，在一定的拐点以后按抛物线的变化规律增长；在距离声源较近的位置，传播损失较小，随着深度和距离逐渐远离声源位置，水声信号的传播损失逐渐增大。