OCT内窥镜驱动控制用微型压电马达的机电耦合动力学特性研究

刘周龙,周 铄,朱强国,郑友成,王光庆

(浙江工商大学 信息与电子工程学院(萨塞克斯人工智能学院),杭州 310018)

光学相干成像技术(optical coherence tomography,OCT)是一种新型的成像检测技术,广泛应用于胃肠道、血管、眼科、皮肤以及肾脏等器官的检测,是光学医学影像研究的前沿和热点[1]。通常,OCT内窥镜前端反射镜的旋转运动是由微型电磁型马达驱动实现的。电磁型马达具有转速高等优点,但其输出力矩小、可控性低、低速需要减速结构,导致结构设计难度和复杂度都增大。

压电马达是利用压电陶瓷(piezoelectric,PZT)的逆压电效应将外界输入的电能转换为超声频域的振动能,并通过定子与转子间的摩擦耦合推动转子实现旋转运动[2]。与电磁型马达相比,压电马达具有低速大力矩、结构设计灵活简单、控制精度高以及无电磁干扰等优点,非常适用于OCT内窥镜的驱动控制[3]。

OCT内窥镜驱动马达受空间尺寸限制,压电马达通常只有1 mm左右大小,设计难度非常大;此外,压电马达是复杂的机电耦合的动力学系统,涉及压电陶瓷与定子之间的力-电耦合、定子和转子之间的摩擦耦合、以及转子与负载之间的力耦合等等。为了有效设计微型压电马达,有必要建立精确的压电马达整体机电耦合动力学模型,该模型建立得越精确,对压电马达的性能预估越准确,压电马达也会设计得越好[4-5]。当前,对压电马达动力学分析方法主要有：等效电路法[6-7]、有限元[8]和解析方法[9]等。等效电路法在马达设计和结构优化过程中无法实时调整马达参数;有限元方法运算量太大、耗时长[10]。

本文针对OCT内窥镜驱动与控制技术要求,同时考虑结构空间尺寸的局限性,利用有限元分析方法设计了直径1 mm长度5 mm的一体化压电微马达。首先利用铁木辛柯梁方法求出定子的振动模态,然后利用Hamiltion变分原理[11],建立能量转换过程,结合定转子之间的接触模型和转子力矩平衡原理,得到微型压电马达的机电耦合动力学模型,仿真分析了压电马达的力矩-转速、力矩-功率和负载特性等。

1 压电马达定子弯曲振动模式

设计开发直径1 mm长度5 mm的圆柱微型压电马达,其包含一种新型定子结构——一体化定子。

一体化定子结构如图1所示,主要包括金属圆柱、两片PZT、金属帽、输出轴以及磁性金属底座。直径1 mm,高5 mm的金属圆柱在加工时会提前切割两个正交的切面,用于粘贴陶瓷片;两片PZT的尺寸为5.00 mm×0.60 mm×0.15 mm、且极化特性完全相同,采用正交90°粘贴在金属圆柱的切割面上,其表面通过点焊方法分别连接两个正交的高频外部激励电压(sinωt和cosωt);压电马达定子固定在磁性金属底座上,形成下端固支,上端自由的梁模型。当两相正交的高频激励电压以相同的幅值和频率加载在两压电陶瓷片上,压电片在电场的作用下发生正交弯曲振动,从而使金属柱状定子表面形成行波[12],并通过定、转子之间的摩擦力驱动转子进行旋转运动。

图1 金属柱状一体化定子结构示意图

为确定压电马达一体化定子的振动模式,把微型马达定子看作一端夹持固定一端自由的悬臂梁模型。

假设PZT的应力-应变满足胡克定律和线性关系。因此悬臂梁在单相正弦激励(例如A相)单独作用时产生的弯矩可以表示为

Mz(t)=μVapp(t)=μVampsinωt

(1)

式中：Mz(t)为在电压Vapp(t)激励下引起均匀分布的弯矩[13];Vapp(t)为压电陶瓷片的激励电压,幅值为Vamp(t),电压频率为ω;μ为比例系数,与压电马达的材料特性和结构尺寸有关,即

(2)

式中参数物理意义及取值详如表1所示。

表1 μ的参数值

根据铁木辛柯梁振动理论[14],悬臂梁中任意一点的振动方程可以用绕度y和弯曲斜率ψ来描述,即

(3)

(4)

式中：E为定子材料的弹性模量,GPa;G为定子材料剪切模量,GPa;I为定子横截面极惯性矩,m4;A为定子横截面面积,m2;J为转动惯量,kg·m2;ρ为定子的密度,kg/m3;k为横截面的形状系数。

假设

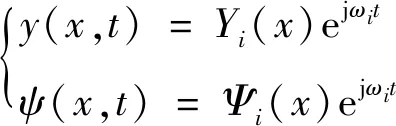
(5)

将式(5)代入式(3)和式(4)中,计算得到Yi(x)和Ψi(x)的通解形式,即

Yi(x)=C1coshbiαix+C2sinhbiαix+

C3sinbiβix+C4cosbiβix

(6)

(7)

压电马达的定子为一端固定一端自由的悬臂梁,则梁的充分必要边界条件为：

固定端

Ψ(0)=0,Y(0)=0

(8)

自由端

(9)

利用通解式(6)、式(7)和梁边界条件式(8)、式(9)求得式(3)、式(4)的特征解以及第i阶振动模态bi。

通过上述条件得到定子梁的第i阶模态变量：横向位移Yi和弯曲饶度Ψi

Yi(x)=D[coshbiaix-λiτiδisinhbiaix-

cosbiBix+δisinbiBix]

(10)

(11)

式中：D和H为无量刚常数,由悬臂梁的边界条件决定,横向位移Yi和弯曲饶度Ψi还满足以下的振动正交条件

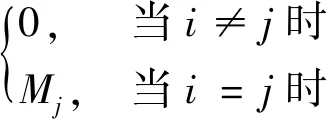
(12)

式中,Mj为广义质量。

压电马达在正交谐波电压激励下,使用模态求和法得到定子的近似响应,即定子的响应形式由其模态与广义坐标qi(t)的乘积和来表示

(13)

在此过程中定子自由端形成均匀分布的弯矩Mz(t),因此式(3)可替换成

(14)

压电定子通常工作在第一阶弯曲振动模式下,因此取第1阶模态进行计算,将式(13)代入式(4)和式(14),考虑到在实际情况下系统存在黏滞阻尼,则A相单独激励时定子运动方程为

(15)

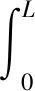
同理,当B相激励时定子的运动微分方程为

(16)

由式(15)解得

sin(ωt-φ)

(17)

同理当施加另一项电压时,其振动幅值相同,位移相差90°。

2 定子质点运动轨迹

假设微型马达定子端面上存在任意一点P(x,y),为方便分析,忽略金属圆柱的切割面,因此定子俯视图可看作半径为r的圆形,如图2(a)所示,O点为定子轴线与上端面中心的交点,θ为方位角,是点P与x轴的偏转角度。

(a) P点俯视示意图

因此在A,B两相单独激励时定子的横向位移分别表示为

yL(t)=Y1(t)q1(t)=γsin(ωt)

(18)

yL(t)=Y1(t)q2(t)=γcos(ωt)

(19)

P点在x,y方向的位移偏量ua,ub简化为

(20)

若A相电压单独激励时,定子表面的质点会产生纵向偏移,如图2(b)所示,纵向位移ωp可通过式(13)、式(17)联合求得。定子梁在外界激励时,其弯曲饶度ψL(t)为

ψL(t)=Ψ1(t)q1(t)=βsin(ωt)

(21)

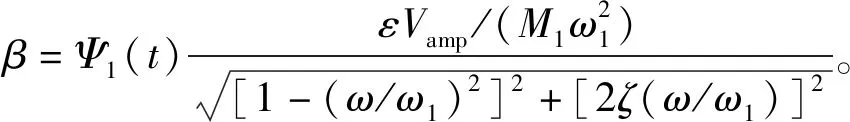
当A相电压单独激励时,其纵向位移为

wpa=-Rβsinθsin(ωt)

(22)

A,B两相电压幅值相同,时间相差90°,则B相的纵向位移为

wpb=-Rβcosθcos(ωt)

(23)

因此当A,B两相同时激励时,定子的纵向位移为两相之和

wp=wpa+wpb=-Rβcos(ωt-θ)

(24)

从式(24)可以发现P点在z方向的位移不仅与时间t有关,还与Ox轴的角度θ有关,位移响应呈简谐波,波数为1,波长为2πr。由于此波没有固定的节点和波腹位置,并且沿着周向旋转,因此认定为行波。

将图2(a)中的P点在A,B两相电压下的横向位移ua,ub沿P点的径向和切向分解,得到P点在径向和切向的位移ur,uτ,表达式为

ur=uasin(θ)+ubcos(θ)=γcos(ωt-θ)

(25)

uτ=uacos(θ)-ubsin(θ)=γsin(ωt-θ)

(26)

从式(25)、式(26)中可得出：P点在切向和径向位移均呈行波方程。

马达在运行过程中定子表面的质点会发生偏转,如图3所示,P点为定子静止时端面的某一点,P0为P点发生偏转后的位置,P1是P0点在xy平面上的垂足,P1P2⊥PP2。因此定子发生偏转后P点在xy水平面的偏移量为PP1,其式子为

图3 P点空间运动示意图

(27)

设过点P的切线方向为x1轴,与x1轴垂直,且与PP0在同一平面的为y1轴。当马达发生偏转时,在x1Py1平面中P在x1方向的位移偏量为PP2,表达式为

PP2=-PP1sin(ωt+θ)=-γsin(ωt+θ)

(28)

y1方向上的偏移量为P0P2,要确定其大小需先求出P0P1与P1P2,P0P1为定子偏转时质点的纵向位移wp,表示为

P0P1=|wp|=-Rβcos(ωt+θ)

(29)

P1P2=PP1cos(ωt+θ)=γcos(ωt+θ)

(30)

P0P2为

(31)

由式(28)和式(31)可以得出定子发生偏转时质点的运动轨迹

(32)

由式(32)可知,A,B两相同时输入幅值相同,相位差为90°的激励电压时,定子表面质点的运动轨迹为椭圆,符合微型压电马达的设计要求。

3 微型压电马达动力学模型

3.1 定转子接触模型

微型压电马达在工作时,定子表面质点会做椭圆运动,而定转子摩擦接触产生的摩擦力会驱动转子旋转。对于转子的运动问题,需重点考虑垂直方向运动和绕轴旋转运动。根据牛顿运动定律[15],转子在垂直方向的力平衡关系可以得到运动方程

(33)

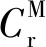
在绕轴运动时,根据力矩平衡关系可以得到其旋转运动方程

(34)

定转子在接触过程中,定子与转子表面会发生力的相互作用,如图4所示。x轴为定子静止时的初始表面,曲线为定子在外界激励时产生的行波波形,定子的行波方向为x轴的正向,转子的运动方向与定子方向相反,即x轴的负向。

图4 定转子的接触界面

假设微型压电马达的定子与转子之间互相紧贴,则定子对转子的压缩量g可等价定子的纵向位移wp,压缩量g与振动位移q1,q2的关系式为

g=-Rψ1(t)[q1(t)sinθ+q2(t)cosθ]

(35)

把转子在接触面上的作用力分解为z相的接触压力fn和水平平面上的摩擦力fd。z向接触力与摩擦层的形变量成正比,摩擦力与fn满足库伦定律,即

(36)

式中：kn为接触点摩擦层等效的刚度系数;μd为定转子摩擦界面的滑动摩擦因数。

对式(36)的第一个式子积分得到

Fint=∬sfndS=∬kngrdrdθ

(37)

同理,式(34)中的MTint可以表示为

MTint=∬sγθfθrdS=∬γθμdkngcos(α)r2drdθ

(38)

式中：γθ为符号函数,由转子速度决定;r为转子半径;fθ,fr分别为fd在切向和径向的分量,即

(39)

式中,α为摩擦角,主要由定子和转子的相对速度决定

(40)

式中：Vr和Vθ为定子在运行过程中某点在径向和圆周切向的速度;Vτ为转子在该点的周向速度,可通过转子的半径乘以其角速度得到。

3.2 接触面能量损失和输出效率

马达在接触界面产生的摩擦损耗功率Pdc可以分为径向滑动[16]和周向[17]滑动引起的损耗Pdr,Pdθ。

Pdc=Pdr+Pdθ

(41)

其中

(42)

(43)

式中：t为定转子接触系统达到稳定状态时的某个时间点;T为对压电陶瓷片施加激励电压的周期。

令定、转子接触界面在运行过程中一个周期的能量传递效率为η,即

(44)

式中,Pout为马达的输出功率,其值为

(45)

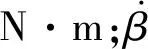
3.3 机电耦合模型及其性能仿真

当马达的A,B两相同时输入激励电压,两相电压分别代入式(15)和式(16),再结合式子(33)、式(34),可推导出能同时描述定子和转子动力学行为的机电耦合模型,其表达式为

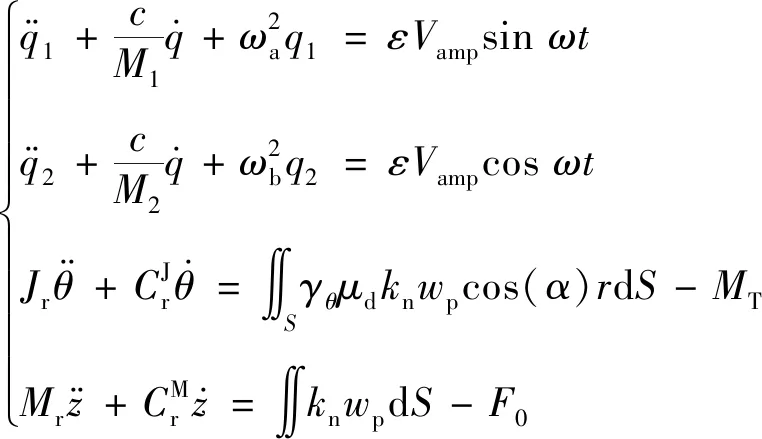
(46)

式中的wp可以用式(35)替换,得到转矩、角速度与振动幅值的关系。

通过式(46)对微型压电马达的输出特性进行仿真,仿真参数如表2所示。

表2 马达仿真参数

将仿真参数代入式(46)的一、二式中,可得到悬臂梁在单相激励下的振动位移。图5(a)与图5(b)分别是定子空载时A,B两相电压单独激励时的振动幅值,其激励电压30 V,电压频率21 kHz。由于激励电压的频率较大,所以振动幅值的周期就越小,间距越密。从图5中可以发现q1,q2的振动幅值随着时间的增大而增大,在0.4 s时定子的振动幅值趋于稳定,即马达达到稳定状态,最大振动幅值为0.6 μm。图6为压电马达在稳定状态时q1,q2振动幅值对比图,q1与q2的振动幅值相同,但q1与q2的位移相位相差90°,与激励电压的时间相位差相同。

(a) A相电压单独激励

图6 q1与q2振幅对比

当马达运行时,转速是不可忽略的输出特性,影响转速变化的因素有电压大小、频率,接触面的摩擦因素、负载力矩、预压力等。

压电马达的激励源为相位相差90°,峰值为30 V,频率21 kHz的交变电压。对微型马达施加不同的负载力矩,观察马达在启动过程中转速的变化。如图8所示,当施加不同负载时,马达在稳定状态时的最大转速会发生变化,负载越大,转速越小。除此之外,马达在空载时启动是瞬间启动,当增加负载时,马达的启动有一个短暂的时延,且负载越大,启动时延越长,如图7所示,负载分别为0.5 mN·m和1 mN·m时,启动时延分别为5 ms和0.04 s。这主要是由于负载增大,定转子接触面的初始摩擦力小于负载的阻力,无法驱动转子运行,因此转速在一段时间内为零。当摩擦力大于阻力时,转子开始加速旋转。马达转速在启动时加速较快,随时间变化其增加趋势趋于缓慢直至达到稳定状态。

图7 启动时电机转速变化

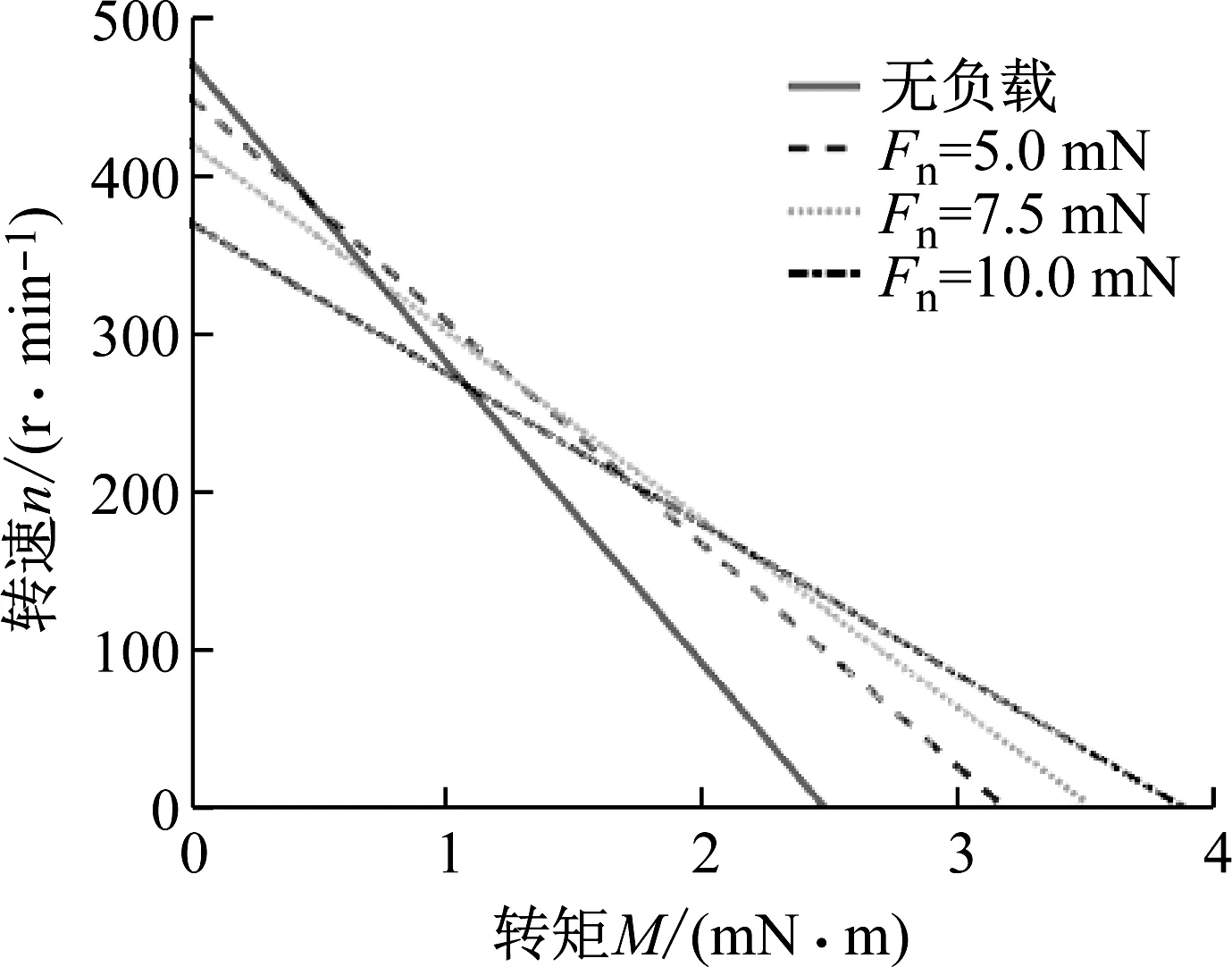
图8 不同压力对马达转速的影响

改变微型马达的预压力,其机械特性的输出效果也会产生变化,在试验过程中,主要通过增加转子上方的垫圈数量改变其预压力的大小。如图8所示,改变预压力的大小马达的转速与力矩呈线性下降,空载时,转速达到最大,堵转时,马达转速降为零,这种情况下马达发热严重,容易烧毁马达。此外,预压力增大,马达的空载转速减小,无压力时,马达的空载转速为470 r/min,当预压力增大到10 mN,空载转速下降到370 r/min;但马达的堵转扭矩会从2.5 mN·m增大到4 mN·m。同时由于马达的预压力增大,马达的负载特性曲线由“软”变“硬”,即马达驱动的最大负载能力逐渐增加。

与传统马达相比,压电马达的输出功率较小。输出功率的变化与转矩有关,会随着转矩的增大先增加后减小,输出功率最大值对应的转矩为最优转矩点。

预压力的变化也会对输出功率产生影响,如图9所示。转子的预压力增大,其最大输出功率先增大后减小,即马达存在最优预压力,此时马达输出功率最大。在预压力增大过程中,堵转力矩也会增大,且最优转矩点随着预压力增大往左偏移。当预压力为7.5 mN时,马达的输出功率达到最大值38 mW。从式(45)中可以看出,输出功率的大小取决于输出转矩与角速度,微型驱动马达的输出转矩在增大的过程中,角速度会降低,当输出功率达到最大值之后,马达转速下降的趋势大于输出转矩增加的趋势,输出功率开始降低,当速度趋于零时,马达的输出功率为零。

图9 压力对输出功率的影响

马达性能的好坏可通过其输出效率来判断。当压电马达工作时,转子转动过程中会在径向和周向发生滑动引起损耗,两者的损耗统称为摩擦损失的功率,损失的功率会随着预压力的增大而增大,如图10所示。其主要原因为预压力增大时定转子的接触界面增加,另一原因是压力增大时,在运行过程中产热增加,增加功率损耗[18]。

图10 不同预压力马达损失的功率

不同的预压力对马达输出效率的影响如图11所示,其变化趋势与马达的输出功率趋势相似。从图11可以发现,只有预压力合适时,马达才会有良好的输出效果,输出效率最大值为预压力7.5 mN时,其输出效率为33%。

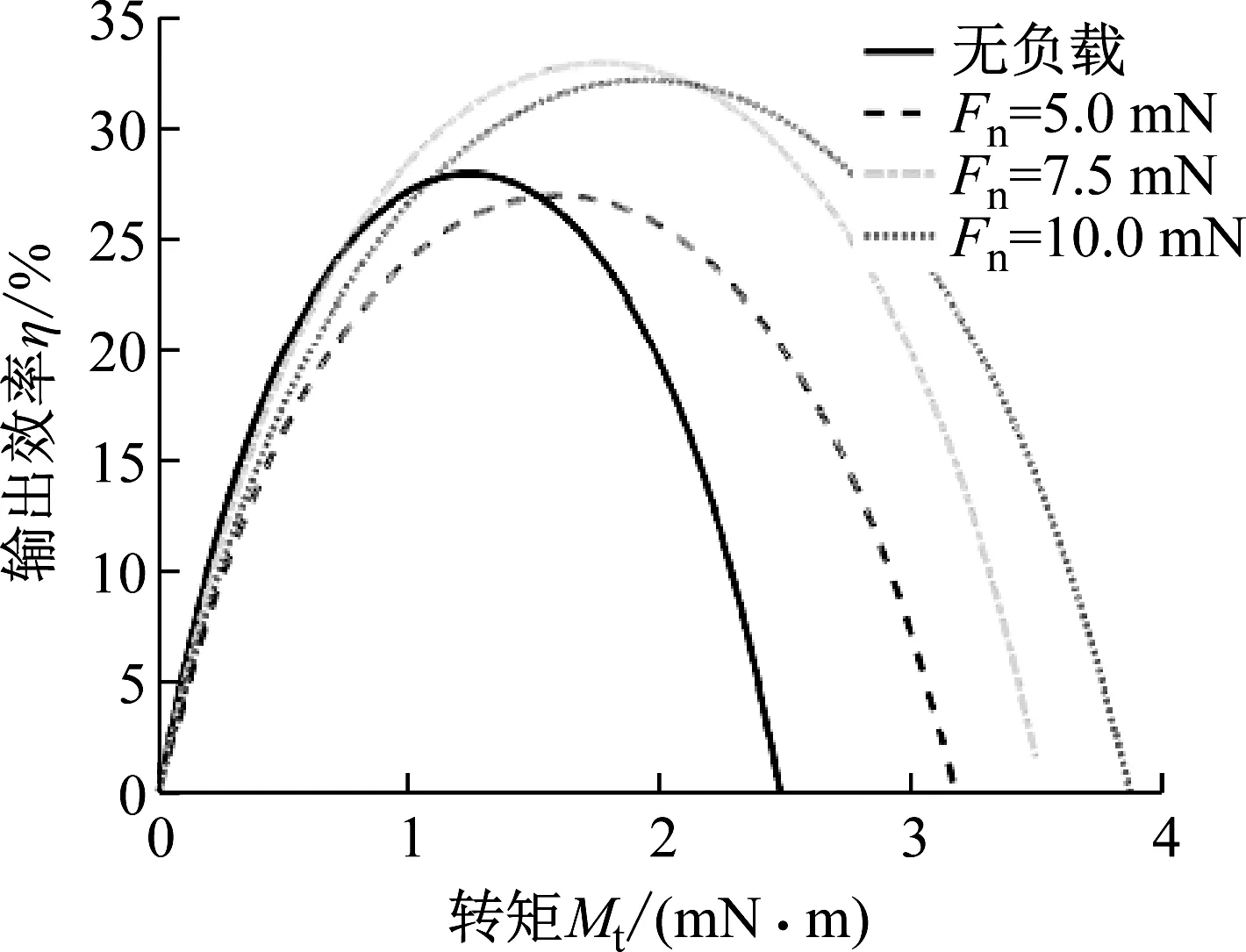
图11 压力对输出功率的影响

4 试验分析

利用两片PZT和长5 mm、直径1 mm的金属圆柱制作微型压电马达样机,马达样机包括一体化定子、磁性金属底座、转子和垫圈,马达总长度为7 mm,如图12所示。

图12的黄线与绿线一端分别与两片PZT焊接,另一端分别连接A,B两相电源,黑线一端连接磁性金属,一端接地。为方便观测在转子侧边粘贴黄色细纸条,转子上方放置垫圈,可通过改变垫圈的数量改变预压力大小,为方便区分,图中的垫圈与转子处于分离状态。

首先利用阻抗分析仪,对微型压电马达样机的阻抗进行测量,图13为试验测得的压电马达阻抗/频率曲线,其第一阶弯曲振动模式谐振频率约为20.5 kHz,与仿真结果21 kHz相仿,表明微型压电马达的样机符合设计要求。

图13 阻抗试验图

由于微型压电马达尺寸较小,转速较快,因此无法通过肉眼直接进行观测,需要借助其他设备辅助测量。

设计了一种检测方法：通过激光位移传感器来检测微型压电马达的转速,下位机传感器与上位机电脑相连。试验过程,压电马达的转子在旋转过程中,每旋转一周,转子侧边的纸片就会经过一次激光传感器发出的激光信号,由于纸片遮挡激光信号,因此上位机监测的位移数值会发生短暂的改变,只需要统计激光位移传感器在1 min内位移发生波动的次数,即可确定马达的转速。激光位移传感器的型号为KEYENCE LK-G80,其最小精度为2 ms,在压电马达的转速范围之内。

图14(a)～图14(d)为电机的试验结果。当改变激励电压的频率,其转速会发生变化,且在第一阶弯曲振动谐振频率附近时,马达的转速较大,激励电压的频率偏离一阶振动频率时,转速减小,见图14(a)。

(a) 频率-转速

对压电陶瓷片输入不同的激励电压时,在一定范围内,马达的转速会随着电压的增大而增大,如图14(b)所示。若在试验过程中输入的电压幅值大于PZT所能承受的最大值,则PZT会被击穿报废。

在试验过程中,增大转子的预压力,马达的堵转力矩会发生变化,堵转力矩通过角加速度法[19]测得。如图14(c)所示预压力增大,堵转力矩增大,相同但其增大的趋势趋于平缓,当预压力达到临界点时,马达则会无法启动。

试验测得预压力增大过程中,马达空载状态下的转速会减小,见图14(d)。试验结果低于仿真结果,但总体趋势一致,主要原因是外界转子与定子之间存在摩擦,以及其他外界因素对试验造成误差。

5 结 论

本文首先利用铁木辛柯梁模型计算得出长度为5 mm,直径为1 mm的微型压电马达的定子的振动幅值响应,结合Hamilton能量变分原理建立马达的机电耦合模型。通过MATLAB软件计算马达的输出特性,考虑不同影响因素对马达输出特性的影响,在一定范围内改变预压力大小后对马达进行仿真。

仿真得出：马达的转速随着负载转矩的增加,转速降低;当马达在有负载的情况下,马达的启动速度会减慢,但达到稳定状态速度一致;预压力会改变马达的输出特性,且存在一个最优点。仿真结果满足马达的制作要求,为微型驱动马达的制作及进一步研发和性能优化提供了基础。不足之处：在仿真马达的输出特性时,在转矩或预压力增大过程中无法考虑马达温度升高对其的影响。

试验结果表明：激励电压的幅值增加,马达转速增大;电压的频率在一阶模态频率附近,其转速较大;预压力增大,马达的最大空载转速会降低,但马达的堵转力矩会增大,试验结果与仿真的误差在允许范围内。

1 mm微型压电马达的一体化定子由于尺寸微小,加工制作时在精确度上会比较困难,但其设计结构易于马达的安装。在试验结果与仿真存在一丝误差,误差的可能原因为外界摩擦的因素以及样机的尺寸精度,在后续工作中会继续提高精度,减少试验误差。