压电圆盘的轴对称振动:改进的双勒让德多项式方法
2023-11-14周红梅韩康乐禹建功张会端王现辉张小明
周红梅,韩康乐,禹建功,张会端,王现辉,张小明
(河南理工大学 机械与动力工程学院,河南 焦作 454000)
压电陶瓷是一种重要的功能材料,具有优良的压电、介电和光电特性,广泛用作传感器和执行器部件,应用于结构的形状控制、振动和噪声主动控制以及结构健康监测等诸多领域。作为具有压电效应的横观各向同性材料,其自由振动问题受到了国内外学者们的广泛关注。该类问题归结为特征值求解问题,目前应用于压电材料自由振动的方法包括解析法[1-9]、半解析法[10]、有限元法[11-14]、数值分析法[15]、无网格法[16]等。其中解析法利用三维弹性理论和压电理论,一维剪切变形理论、弹性薄板理论等,将位移和电势扩展成无穷级数的形式,代入求解特征值问题来获得振动频率及谐响应。Kim等[3]利用圆柱膜理论推导出二维控制方程,应用力学和电学边界条件,得到了压电开壳换能器谐振频率的特征方程,计算了基频和机电耦合系数。Li等用广义超几何函数代替横观各向同性压电陶瓷轴对称电场的精确解,分析了安装在金属轴上的径向极化圆柱形压电驱动器的轴对称振动特性。Razavi等利用一致耦合应力理论和圆柱壳模型,建立了功能梯度压电材料纳米圆柱壳的机电振动控制方程,研究了特殊模型在不同边界条件下的自由振动。林书玉[17]对压电陶瓷圆环径向振动进行了研究,由机电等效电路,推导出了压电陶瓷圆环振子的共振和反共振频率方程。
勒让德多项式方法最早由Lefebvre等[18]应用到导波传播求解,该法通过将边界条件导入到传播控制方程,将微分方程转化为特征值来求解问题。之后,Elmaimouni等[19]提出了一种无限长均匀各向异性弹性材料圆柱杆中导波传播的多项式方法,计算了其归一化频率。Raherison等[20]将勒让德多项式方法扩展到体波谐振器的建模方面,得到了Al/ZnO/Al夹心板体波谐振器的谐振频率和反谐振频率。Elmaimouni等[21]将映射正交函数法推广到考虑电源的三维声波问题中,得到了一维解析模型下特定几何形状的归一化频率和电输入导纳。
由于双勒让德多项式法可以通过添加矩形窗函数将压电材料两个方向上的边界条件加入其振动控制方程,现将其引入到压电圆盘的振动特性研究,但传统计算方法因求解过程的积分函数引入了双勒让德多项式级数、矩形窗函数及其导数,处理数值积分需要大量的运算时间,尤其高阶数值积分计算相当费时,而低阶时谐振频率值收敛性较差,因此限制了双勒让德多项式法在压电材料振动控制方程求解中的应用。为了解决计算缓慢这一问题,本文对双勒让德多项式的传统求解方法进行改进,引入解析积分过程,用解析积分代替传统数值积分的方法,使得程序计算时间大大缩短。
1 振动控制方程及求解
极化后的压电陶瓷是横观各向同性材料,一般规定极化方向为Z轴方向。若在垂直于Z轴方向压电圆盘的上下表面加上金属电极,可近似认为只存在轴向电场Ez(忽略电极的边界效应),因加上的电极很薄,其质量和刚度也可以忽略不计。由于压电圆盘的几何结构、外加电场和约束条件都是轴对称的,故压电圆盘作轴对称振动。基于三维线弹性理论,假设压电材料上下表面和侧面应力自由机械边界条件,侧面电开路、上下面电短路电边界条件。考虑材料结构为圆盘,故采用柱坐标系(r,θ,z),压电圆盘的结构示意图如图1所示,其中V0jωt为压电圆盘外加电源。

图1 压电圆盘
压电材料的本构和压电方程为
(1)
式中:i,j,k,l=1,2,3;σij,εkl,EkDi分别是应力、应变、电场强度和电位移;Cijkl,ekij和δik分别为弹性常数、压电常数和介电常数。
式(1)在柱坐标系中展开分别为式(2)和式(3)
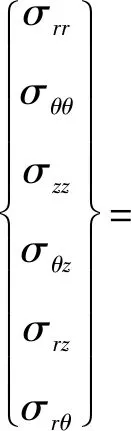
(2)

(3)
其中电场强度用式(4)表示
(4)
式中,φ为电势。
式(2)、式(3)中的应变满足下列几何方程
(5)
式中,u,v,w分别为r,θ,z方向的位移。
基于三维线弹性理论,假设在柱坐标系下的边界条件
考虑到边界条件的处理问题,引入两个方向(r和z)的矩形窗函数
将式(4)和式(5)代入式(2)和式(3)并添加上述矩形窗函数,分别得到式(6)和式(7)
(6)
(7)
不考虑体力和体电荷,压电圆盘的振动控制方程为
(8)
压电圆盘作轴对称振动,所以振动与方位角θ无关(∂/∂θ=0,v=0),式(5)、式(6)对应项为0,式(8)中第二项都为0。将式(6)和(7)代入式(8)得到
(9)
(10)
(11)
式中,u(r,z),w(r,z),φ(r,z)分别为径向位移、轴向位移和电势,其解的形式可以用多项式表示为
(12)
(13)

(14)

(15)
(16)
式中,Pm和Pn分别为第m阶和n阶勒让德多项式。理论上m和n从0变化到∞,而实际上对于求和多项式(12)~式(14),当m和n取到有限值m=M和n=N时,更高阶的项可以认为是高阶小量,忽略不计。
将式(12)~式(14)和式(15)、式(16)代入式(9)~式(11),利用不同次数的勒让德多项式在区间[-1,1]上正交的特性,用Qi(r)Qj(z)e-jωt乘各式的两边,i从0变化到M,j从0变化到N,再将各式对z从-1到1、r从-1到1积分,利用其正交特性,式(9)~式(11)可转换为下列形式
(17)

为了便于计算,取

(18)
与此同时,求出式(17)中的rm,2n+1并代入式(18),可以得到
[ABC+Ω2MM]pm,n=CfV0
(19)
式中:ABC=AB-CC(C3)-1AB3;Cf=CC(C3)-1·f3-f1,2。
由压电材料的谐响应特性可知,谐振频率点处的阻抗很小,即此时模型电极间的电势很小,近似为零。将V0=0代入式(19),即可得到求解谐振频率的特征方程
(MM)-1ABCpm,n=-Ω2pm,n
(20)
利用特征矩阵求特征值,可得归一化频率Ω。
计算过程中引入解析积分法,使得程序计算时间大大缩减。解析积分法转换前公式为
(21)
转换后为
(1) 当a+m≥n和a+m-n=偶数
当a,m,n取其他值时,I1=0。
(2) 当a+m-1≥n和a+m-n-1=偶数
当a,m,n取其他值时,I2=0。
(3) 当a+m-2≥n和a+m-n-2=偶数
当a,m,n取其他值时,I3=0。
(22)
2 数值算例
为了验证该方法的准确性和高效性,本章给出了两种材料压电圆盘的自由振动分析算例。其中材料参数如表1所示。本文程序用MATLAB 2018b编制,运行电脑配置 CPU为Inter core I7-4790,3.6 GHz,内存为16 G。

表1 材料参数
2.1 算例1
首先以PZT4压电圆盘(R=12.4 mm,H=2.05 mm)为例,将本文解析法与传统方法进行比对,并与已有文献结果对比,如表2所示。

表2 解析法与传统方法结果对比
从表2可以看出随着双勒让德多项式阶数(M,N取值)的增大,压电圆盘的谐振频率低阶快速收敛,高阶相对收敛较慢,相同阶数传统求解时间比解析法求解时间多数百倍,传统法随着阶数增大,耗费CPU时间剧增以致7阶以上无法求解。通过与文献结果比对发现M=N=15时前3阶的误差均在0.5%以下。
为了分析压电圆盘固有频率与径厚比的关系,PZT4压电圆盘厚度H=2 mm,改变圆盘直径,图2给出了不同径厚比对应的圆盘固有频率半径积。图2给出了前3阶模态关系曲线,从图2可以看出随着径厚比增大到5之后频率半径积趋于稳定,而且低阶更快达到稳定。图2中小图是[1,4]区间细化后的图,明显3阶频率半径积都是先增大再减小到固定的稳定值。

图2 PZT4压电圆盘频率半径积随径厚比关系
以径厚比R/H=10,H=2 mm为例,其径向u和轴向w位移如图3和图4所示,从图3、图4得出u向关于厚度中面对称分布,半径大小对前3阶位移影响较小。w向位移对于H中面呈反对称分布,同样半径大小对低阶影响较小。
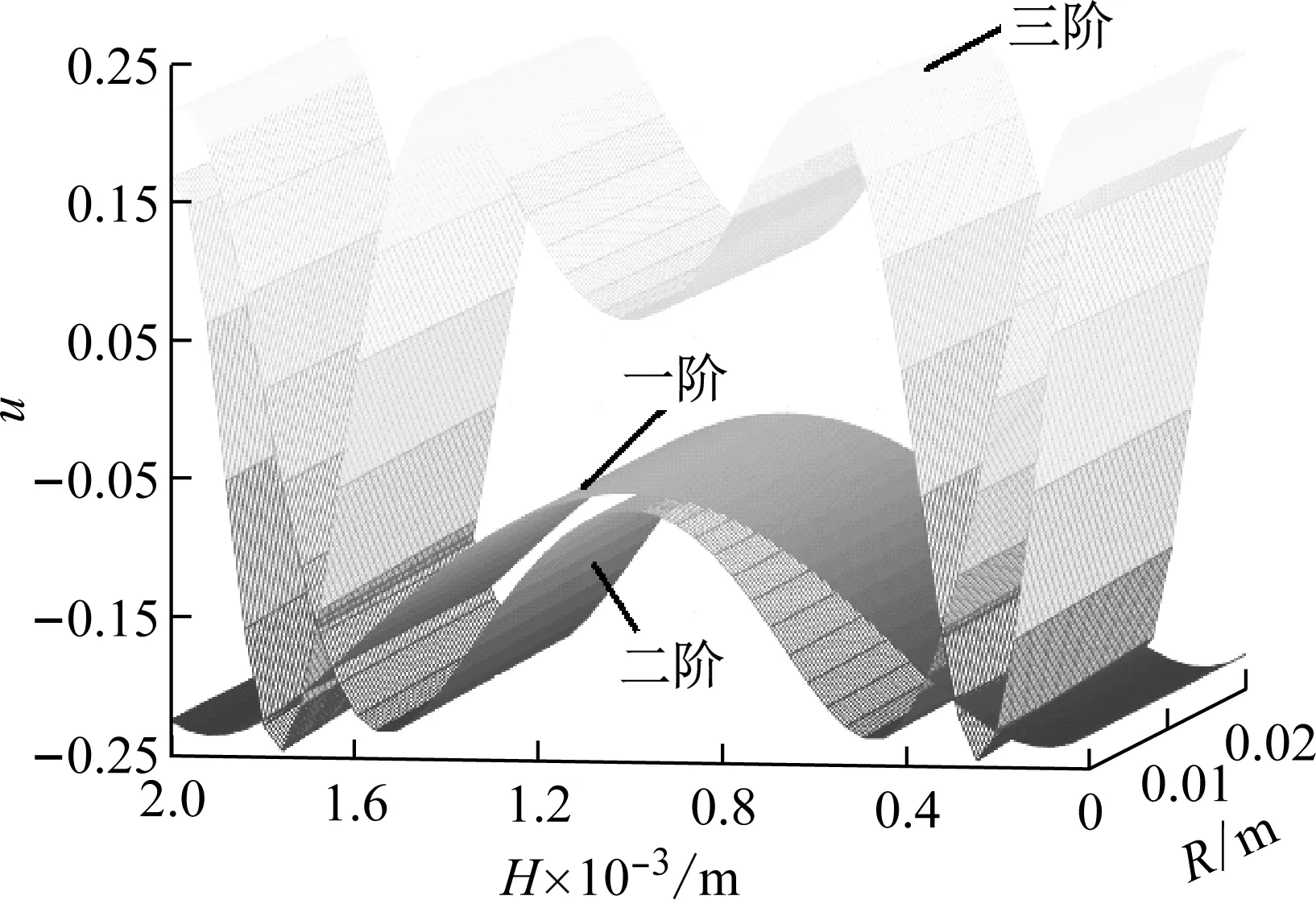
图3 PZT4压电圆盘u向位移
为了分析压电圆盘固有频率与厚度变化关系,PZT4压电盘R=50 mm,改变其厚度H,图5显示不同厚度圆盘固有频率前3阶数值。从图5可明显看出厚度在[2,10]内也就是径厚比在[5,25],固有频率随厚度变化较小。图2~图5所用双勒让德阶次M=N=15。

图5 PZT4压电圆盘频率随厚度变化关系
2.2 算例2
材料为PZT5A,R=20.05 mm,H=2.03 mm,得到其谐振频率如表3所示,其中理论计算是通过电输入导纳计算获得。

表3 PZT5A压电圆盘谐振频率(R/H=10,M=N=15)
对于薄圆片的径向振动模式可以通过式(23)计算电输入导纳,结果见图4。
(23)
从表3可以看出谐振频率前两阶与文献[22]相比误差较小,在0.5%以内。高阶时误差逐步增大。通过引入电输入导纳理论计算获得数据与本文方法高度吻合,5阶的误差仅为0.54%,进一步验证了本文方法的准确性。
3 结 论
本文应用三维压电弹性理论,结合力电耦合的本构方程、几何方程和振动控制方程,把位移和电势分别扩展成相乘的包含待定系数的双勒让德多项式级数,然后利用多项式的正交性分别与不同阶的正交多项式相乘,并在R和Z方向进行积分,得到关于频率的特征方程,其特征值为压电陶瓷振动的谐振频率,特征向量为勒让德多项式级数的待定系数,可转化为压电陶瓷的谐响应。
多项式级数法的边界条件处理是将应力和电位移乘上限定边界的矩形窗函数,把边界条件直接添加到振动控制方程中,在后续积分中消去矩形窗函数。但是求解过程因为积分函数引入了勒让德多项式级数、矩形窗函数及其导数,处理数值积分需要大量的运算时间。为了解决这一问题,本文引入解析积分法,导出了用解析积分代替数值积分的转换公式,使得程序计算时间大大缩短。将计算结果与文献及理论结果进行了对比,充分说明了方法的准确性与高效性。
勒让德多项式方法可以直接把变系数的弹性常数引入本构方程[23]。因此,本文所提出的改进方法在求解功能梯度结构、黏弹性结构的振动问题时也将有较大优势。
