考虑惯性载荷的多材料结构拓扑优化

任毅如 ，杨林海 ，米栋 ，张立章 ，何杰 ，向剑辉

（1.湖南大学 机械与运载工程学院，湖南 长沙 410082；2.中国航发湖南动力机械研究所，湖南 株洲 412002）

拓扑优化指在给定的设计域内不断优化设计变量使得结构在满足设计要求的同时达到材料分布的最优解，其由于具有优化自由度高、材料利用率强的优点，被广泛应用于汽车设计、航空航天、声学等领域［1-3］.

1981 年程耿东［4］对实心弹性薄板的优化研究，被认为是连续体结构拓扑优化的奠基性工作.各算法相继被提出用于解决拓扑优化问题.然而在早期的拓扑优化问题中，研究重点大多侧重于施加外部载荷作用下的优化，惯性载荷作为与设计结构质量直接相关的载荷往往被忽略［5］，以此得出的优化结果应用于实际工程问题是不可靠的.Rozvany 等［6］首先提出了关于自重的优化设计问题.陈树勋和叶尚辉［7］为解决天线设计问题提出了导重法.Bruyneel等［8］对固体各向同性材料惩罚模型（Solid Isotropic Material with Penalization，SIMP）进行了修正，来改善惯性载荷作用下结构拓扑优化中低密度区域存在的寄生效应.Huang 等［9］开发一种新的带有插值函数的双向结构渐进优化方法（Bi-directional Evolutionary Structural Optimization，BESO），在对具有自重的结构进行优化时相比较SIMP 插值模型能够获得更好的优化结果.Xu 等［5］指出在使用导重法时，RAMP 插值函数相比其他插值方法更适用于惯性载荷作用下结构的拓扑优化.Jain等［10］研究表明自重对结构的最优拓扑有显著影响，结构的拓扑构型取决于外加载荷和结构自重的双重作用.Kumar［11］提出了一种基于密度的拓扑优化方法来设计自重载荷下的结构，并利用Heaviside函数得到一种新的质量密度插值策略.

同时在结构设计中，轻量化和性能要求越来越高，多材料混合结构能够在多方面更好地满足设计需求，增材制造技术的发展也使得多材料结构拓扑优化从理论设计变为现 实［12-13］.Huang 等［14］采 用BESO 来解决多相结构拓扑优化问题.Tavakoli 等［15］将多材料拓扑优化问题分解为多个单材料拓扑优化子问题并提供了一个可在MATLAB 上运行的通用框架.Zuo 等［16］提出了一种单变量有序SIMP 插值方法，用于质量约束和成本约束下的多材料拓扑优化.刘继凯等［17］提出了基于Ordered SIMP 方法的点阵-实体多材料插值模型.Gao等［18］使用交替有源相位法与蒙特卡罗模拟相结合来解决多材料的拓扑优化问题.

多材料下的多个优化变量增加了优化求解的复杂性，且在解决惯性载荷作用下结构拓扑优化问题时，由于密度趋于0，质量惩罚与刚度惩罚之比过大，在低密度区域结构的位移和柔度趋近于无界，由此产生寄生效应［8，19］，更是加大了拓扑优化的难度.目前针对惯性载荷下的多材料结构拓扑优化的相关研究还较少.基于上述研究，本文将通过数值算例对比提出基于RAMP 插值模型的导重法，并将其应用于考虑惯性载荷作用下多材料结构拓扑优化问题.研究体积约束下柔度最小的多材料结构拓扑优化，提供多材料组合下的优化方案.

1 基于导重法的优化模型

1.1 体积约束下的多材料结构优化模型

进行多材料结构拓扑优化时假设共有p相材料，N个单元结构，将孔洞材料看作一种材料，传统的单材料结构拓扑优化即为二相材料结构拓扑优化.在进行多材料结构拓扑优化时，将所有材料两两组合，p相材料拓扑优化即被分解为p（p+1）/2 个二相材料结构拓扑优化，再对每个优化组合运用导重法进行求解.优化时其余组合保持不变.优化过程中，将弹性模量较大的材料称为a材料，较小的称为b材料.在一个循环中，体积约束下的以柔度最小为目标的多材料结构拓扑优化数学模型如下.

1.2 不同插值模型下的迭代公式

对于多材料结构拓扑优化，其弹性模量插值公式为：

式中：Ea和Eb为材料a，b的弹性模量；f()为插值函数模型.

常见的插值函数模型有RAMP、SIMP、EAMP.用式（3）表达，其中qR、qS、qE分别为不同插值模型的惩罚因子.

将柔度对设计变量进行求导，获取关于柔度的灵敏度［式（4）］，其中ki和ui分别为单元刚度矩阵和单元位移向量矩阵.

当Fi为固定载荷时，∂Fi/=0，见式（5）；当Fi为惯性载荷时，其大小随着每次迭代优化改变而变化时，式（4）不变，根据四节点矩形单元的形函数可得到每个单元的等效节点载荷［式（6）］.

其中，Gi和mi为单元重量和单元质量，wi为结构旋转的角速度，ri为各单元至旋转轴的距离，P0=[0-10-10-10-1]，P1=[1 0 1 0 1 0 1 0] 分别为自重和离心作用下的方向矢量.

根据库恩塔克条件由式（1）可推导出：

为确保设计变量迭代的收敛性，引入步长因子m0［20］，本文取m0=0.5.为减少计算量采取二分法来求解λ.将上式代入即可得到的迭代式.当相邻迭代步中误差小于0.001时，优化结束.

2 数值算例分析

2.1 不同插值函数对优化进程的影响

为了比较SIMP、RAMP、EAMP 插值方法对导重法处理惯性载荷作用下多材料结构拓扑优化问题的影响，分别采用这三种插值方法对经典简支梁模型进行优化，体积约束设置为0.3，使结构的目标函数即柔度最小.惩罚因子选取合适大小.同时为方便对优化结果的可制造性进行定量分析，引入灰度因子Mi，由式（11）可以看出，Mi数值越大，代表优化结果中间密度单元越多，优化结构的可制造性也就越差.

图1 为简支梁（算例1）模型图，其两端固定，长120 m，高30 m，离散后的单元数目为3 600，泊松比V统一设置为0.3.只受到自身的重力影响.在优化对比中设置了二相材料（即单材料）结构以及三相材料结构，其弹性模量及体积占比见表1.密度统一设置为1 kg/m3.

表1 多材料下算例1的参数设置Tab.1 Multi-material parameters setting for example 1

图1 算例1模型图（单位：m）Fig.1 Model diagram of example 1（unit：m）

划分为黑色、红色.由图2 可以看出，使用不同的插值函数对于不同相数材料结构的优化结果都是大致相同的，优化结果呈现经典的“拱桥”形状，在三相材料优化结构中，弹性模量大的材料集中在主拱圈处.其次使用SIMP 插值方法在惯性载荷作用下的材料结构优化中无法得到清晰的拓扑图形，存在明显的灰度单元，且在得到初始稳定拓扑形状后其目标函数随着迭代而缓慢升高.使用RAMP 和EAMP插值方法能够得到清晰的拓扑图，目标函数相对更低，其原因在于在低密度区域，RAMP 和EAMP 插值方法中的是有界且维持在一个小范围内，而SIMP 插值方法的在低密度区近于无界，因此不可能实现一个较好的0～1分布优化［5］.

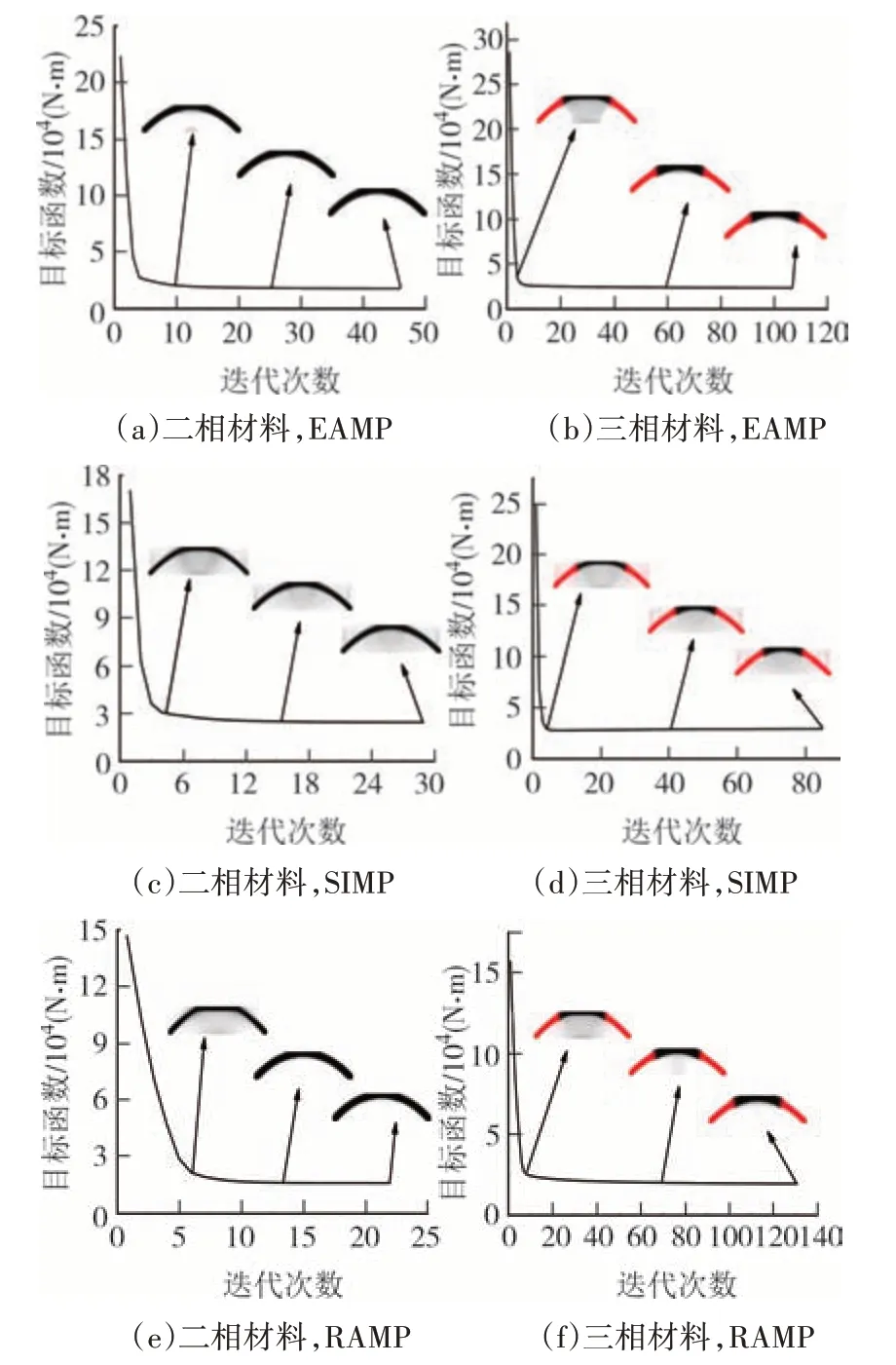
图2 不同插值模型的优化进程图Fig.2 Optimization process diagram of different interpolation models

从表2可以看出，使用RAMP插值方法获得的最终拓扑图其目标函数和灰度因子明显小于EAMP 和SIMP 插值方法，利用RAMP 插值函数对结构进行拓扑优化后在二相材料下得到的目标函数相比EAMP插值函数减少8.2%，对比SIMP 插值函数减少了35.2%，三相材料下相比EAMP插值函数减少16.1%，对比SIMP 插值函数减少了33.1%，且需要的迭代步数与其他方法比较接近.显然在运用导重法解决惯性载荷下结构的拓扑优化问题时，RAMP 插值方法明显优于EAMP和SIMP插值方法.

表2 不同插值模型下的优化结果Tab.2 Optimization results of different interpolation models

2.2 多载荷作用下的数值算例

上节已验证了基于RAMP 插值函数的导重法在处理惯性载荷下多材料结构拓扑优化的优越性，本节将其应用于同时包含集中力与惯性载荷的多载荷拓扑优化问题，且其结构优化将包含更多相数的材料.

2.2.1 自重与集中力载荷作用

悬臂梁（算例2）模型图如图3 所示，长80 m，宽40 m，共计3 200个单元，其受自身重力影响，同时为防止优化过程中悬臂梁末端低密度区域造成优化结果不收敛，在其末端的中点处施加一个质量点，大小为自身重力的25%.

图3 算例2模型图（单位：m）Fig.3 Model diagram of example 2（unit：m）

结构的多材料参数如表3 所示，密度统一设置为1 kg/m3.厚度设置为1 m，重力加速度为9.8 N/kg.根据式（7）可以推导出算例2 所受重力的表达式.在体积约束设置为原材料的30%的情况下使得整体结构的柔度最小.

表3 多材料下算例2的参数设置Tab.3 Multi-material parameters setting of example 2

不同材料依据其弹性模量由大到小分别用黑色、红色、蓝色、绿色表示，即E黑＞E红＞E蓝＞E绿.如图4所示，基于RAMP插值函数下的导重法应用于受自重和集中力作用下的结构拓扑优化，拓展到5 相材料所得到的优化图依旧清晰可见，且优化结构保持一致，呈现桁架结构，其拓扑构型在力的传递方面表现合理.其中弹性模量最大的材料分布在固定端及结构顶端，除去固定端，距离固定端越远，其材料的弹性模量越大.这是由于距离固定端越远，所受自重影响越大，所在设计区域分布材料弹性模量越大.由图5 可以看出，目标函数随着迭代次数的增长而下降，且在迭代初期就趋于最终解.随着材料相数的增加，最终优化结果的目标函数依次升高.这是因为加入了弹性模量较小的材料，导致其整体刚度降低，符合预期结果.

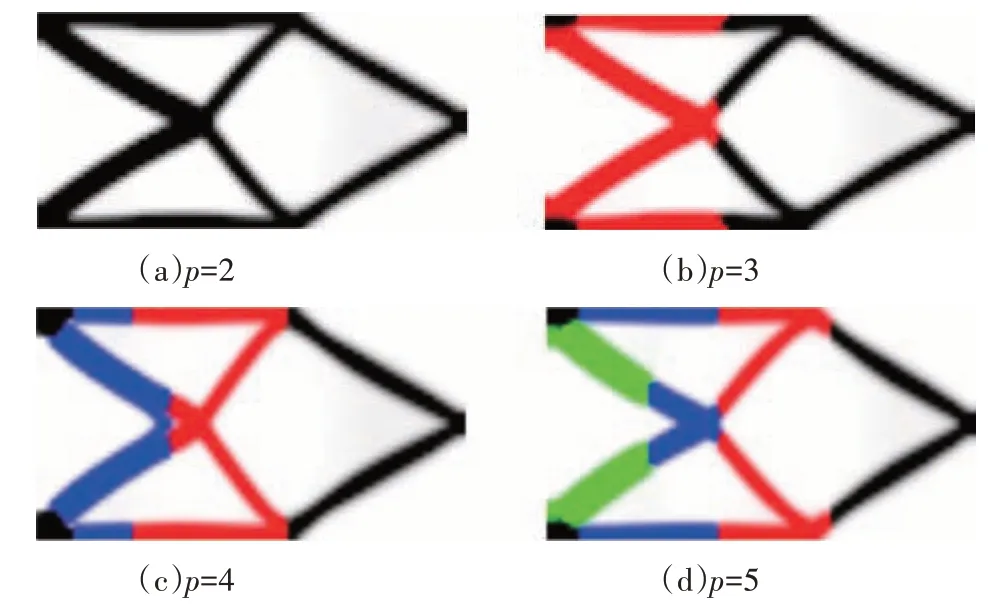
图4 多材料下算例2的优化结果图Fig.4 Multi-material optimization plots of example 2

图5 算例2的目标函数迭代曲线Fig.5 Objective function iteration curve of example 2

2.2.2 离心力与集中力载荷作用

受离心力悬臂梁（算例3）模型图如图6 所示，长80 m，宽40 m，共计3 200个单元，绕着固定端以恒定角速度旋转，ω为旋转角速度取2 rad/s，mi为单元质量，ri为各单元到旋转轴的直线距离，F为质量点，施加在结构末端的中点区域，为总重力的1.2 倍.各材料参数如表4 所示，体积约束设置为30%，使得整体结构的柔度最小.

表4 多材料下算例3的参数设置Tab.4 Multi-material parameters setting of example 3

图6 算例3模型图（单位：m）Fig.6 Model diagram of example 3（unit：m）

算例3 的优化结果图和目标函数迭代曲线分别如图7、图8 所示.可以看出结构在离心力和集中力作用下优化构型呈三角形，由固定端上下两侧连接至末端中点区域.结论与上节类似，结构绕固定端旋转时，距离固定端越远，所受离心力影响越大，其所在设计域分布的材料弹性模量越大.目标函数随着材料相数的增加依次升高.

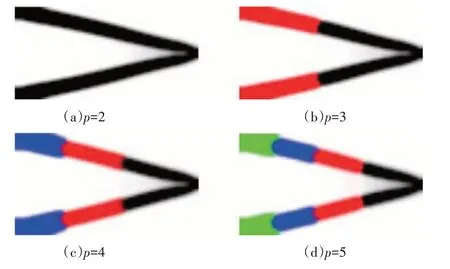
图7 多材料下算例3的优化结果图Fig.7 Multi-material optimization plots of example 3

图8 算例3的目标函数迭代曲线Fig.8 Objective function iteration curve of example 3

3 多材料组合下的优化策略

在上节中已经证明了导重法在处理惯性载荷下多材料拓扑优化问题的可靠性，本节将在体积约束的前提下，通过自重情况下简支梁（算例1）的拓扑优化，论证多材料结构优化下，如何选取不同参数的材料使得目标函数即柔度较低.选取以下3 种材料，其材料参数如表5 所示，为更直观研究参数对于目标函数影响，将所选材料参数进行归一化，使得其数值的绝对值转变为相对值关系，所选取材料的弹性模量和密度最大值被映射为“1”［21］.进行归一化处理后如表6 所示，在优化图中显示的颜色分别为黑色、红色、蓝色，其中Ei、ρi分别为材料的归一化弹性模量及密度.图9为在体积约束为0.3的条件下，对3种材料排列组合进行优化的结果.从图9 可以看出，通过改变材料组合并不改变优化结构形状，分布规律与上节结论相同，弹性模量最大的材料分布在固定端及结构顶端.在单独使用B 材料进行拓扑优化时所得结构的柔度最大，单独使用C 材料时柔度最小即此时刚度最大，最满足设计需求.这是由于C 材料的归一化模量密度比（Ei/ρi）最大［21］.

表5 各材料参数Tab.5 Materials parameters

表6 不同材料的归一化参数Tab.6 Normalized parameters for different materials

图9 多材料组合下的优化结果Fig.9 Optimization results of multi-material combination

4 结论

本文主要研究单一体积约束条件下柔度最小的考虑惯性载荷作用的多材料结构拓扑优化问题，通过不同数值算例的对比，确立了基于RAMP 插值函数的导重法，能够有效减少优化结果的灰度单元，有助于获得清晰的拓扑构型，降低结构的整体柔度.并有下列结论：所受惯性载荷的影响越大，所在设计区域分布材料弹性模量越大；选取不同材料用于多材料结构拓扑优化设计，材料的模量密度比越大，结构的整体柔度越小，刚度越大，对于实际工程应用有着一定的指导作用.