输入时延下约束不确定系统的有限时间控制

王芳 ，赵瑞莹 ，周超

（1.燕山大学 理学院，河北 秦皇岛 066004；2.河北农业大学 海洋学院，河北 秦皇岛 066003）

与线性系统相比，非线性系统能够更好地描述实际工程应用系统.近年来，已经有大量关于非线性系统控制的研究成果［1-6］.反步控制是常用的方法之一，但是，在反步设计过程中，虚拟控制输入的连续求导会产生“计算爆炸”问题.针对这一问题，Zhou等［7］和Li等［8］提出了一阶滤波器，但是没有考虑滤波误差的影响.Wang 等［9］首次针对指令滤波器进行了研究.基于Wang等的滤波器，文献［10-12］研究了不确定非线性系统的控制.文献［7-12］中系统获得了良好的跟踪效果，但并未考虑有限时间稳定.

收敛速度是衡量系统性能的一个重要指标，有限时间控制可以使系统具有更快的响应速度以及更好的抗干扰能力.Yu 等［13］针对非线性系统提出了基于反步法的有限时间控制策略.Xu 等［14］考虑带有未建模动态的非线性系统，并设计了有限时间反步控制器.Liu 等［15］结合有限时间控制和预定性能函数，提出了自适应控制策略.Shen 等［16］考虑进场车辆的控制问题，构造基于积分终端滑模面的快速有限时间收敛控制器，并给出了收敛时间的显式估计.

文献［13-15］在反步控制的框架下研究了高阶非线性系统的有限时间跟踪控制.针对反步控制的“计算爆炸”问题，Cui 等［17］考虑输入饱和下的非线性系统，采用一阶滤波器处理“计算爆炸”问题，并设计了有限时间反步控制策略.有限时间滤波器在解决“计算爆炸”问题的同时，有助于闭环系统实现有限时间稳定.Wu 等［18］针对多智能体系统，提出基于有限时间滤波器的反步控制策略，实现了系统的实际有限时间稳定性.Yu 等［19］针对具有死区的非线性系统，结合指令性滤波器和事件触发机制设计了有限时间控制策略，但是提出的有限时间滤波器只含有非线性部分，可能会导致滤波器状态在远离平衡点时收敛速度较慢.本文将设计新型有限时间滤波器.另外，Wu 等［18］和Yu 等［19］没有考虑输入时延问题.输入时延会导致系统的响应变慢，影响系统的实时性能.而有限时间控制可以确保控制系统在规定时间内完成控制目标，从而提高效率.因此，考虑输入时延下的有限时间控制很有意义.

系统的运行过程中，如果输出违反约束条件，不仅会严重影响系统的性能，还可能造成安全事故，因此，输出约束是设计控制系统时值得考虑的问题.障碍Lyapunov 函数［20-23］能有效解决输出约束问题.Tee等［20］利用障碍Lyapunov函数解决了非线性系统的常数输出约束问题.Liu 等［21］进一步研究了时变输出约束问题.Sun等［22］使用障碍Lyapunov函数研究了高阶非线性系统的输出约束问题.Liu等［23］基于积分障碍Lyapunov 函数处理了输出约束问题.然而，上述文献利用障碍Lyapunov 函数解决输出约束问题时，可能会使控制器设计更加复杂.Meng等［24］和Tran等［25］利用状态变换方法解决了输出约束问题，但把输出约束问题转化为输出误差约束问题时，没有考虑输入时延对系统的影响.

实际系统中，输入时延不可避免，如何减弱输入时延的影响，提高控制效果是值得讨论的问题.Pade 近似法能在统一的框架下处理输入时延，极大程度简化了控制器的设计.Li 等［26］采用Pade 近似法处理输入时延，通过障碍Lyapunov 函数解决输出约束问题，并设计了模糊控制策略.随后，Min 等［27］和Zhou 等［28］结合神经网络和障碍Lyapunov 函数，研究了带有输出约束和输入时延的非线性系统的控制问题，但考虑的是对称的常值输出约束，并没有考虑系统的有限时间稳定问题.本文综合考虑时变非对称输出约束和输入时延对非线性系统的影响，在反步控制的框架下，设计有限时间控制器，以实现闭环系统的有限时间稳定性.

基于以上分析，本文针对非线性系统，考虑输入时延和非对称时变输出约束的影响，设计自适应有限时间反步控制策略：1）设计新的非线性状态变换函数，直接对系统输出进行约束，适用于时变、对称及非对称的约束情形；2）设计新型有限时间滤波器解决反步控制的“计算爆炸”问题，同时通过补偿机制消除滤波误差的影响；3）利用Pade 近似法消除输入时延对控制效果的影响；4）通过Lyapunov 稳定性理论，证明闭环系统的实际有限时间稳定性，同时输出满足约束条件.利用滤波器对比仿真及机械臂系统的应用仿真体现控制策略的优越性.

1 系统描述和预备知识

1.1 系统模型

考虑一类非线性系统：

控制目标：设计有限时间反步控制器，使闭环系统实际有限时间稳定，系统输出在满足约束条件的前提下能够跟踪参考指令yd.

实际有限时间稳定性的定义由如下引理给出：

引理1［12］对于系统=f(x)，若存在正定函数V(x)：D∈R，λ1，λ2，b＞0，h∈(0，1)及关于0 的开邻域 Ξ ⊂D，使 得(x) ≤-λ1V(x)-λ2Vh(x) +b，x∈Ξ{0}，则平衡点x=0 是实际有限时间稳定的.此外，存在0 ＜γ＜λ1和T(γ，x0)＜+∞使得

其中，t0为系统运行的初始时刻.

1.2 假设及引理

假设1期望轨迹yd及已知且有界.

引理3∀si∈R，0 ＜m≤1，则

引理4若h＞1，x＞0，y≤x，则(x-y)h≥yh-xh.若h，y＞0，x≥0，则xh(y-x)h＜

1.3 系统转换

本节采用如下的Pade 近似法补偿输入时延，以消除输入时延的影响：

其中，ℓ{u(t)}是u(t)的Laplace 变换，s是Laplace 变量.定义

因此，系统（1）转变为如下形式：

注1 系统（2）中的xn+1不是系统的真实变量，而是中间变量，不会对控制器的设计造成影响.

注2 时延应小于系统的响应时间，以免影响系统的稳定性.若输入信号变化较快，应选择较小的时延.

注3 由文献［29-30］可知，采用Pade近似法处理输入时延时，较大的时延会使系统的响应变慢以及e-τs≈[1-(τs/2)]/[1 +(τs/2)]的误差增大，致使逼近精确度降低甚至系统不稳定.因此，Pade 近似法只适用于短时延情形，不适用于长时延情形.

1.4 非线性变换函数的构造

为了解决输出约束问题，构造如下非线性函数：

式 中：p1(t)、p2(t)是连续的正时变函数；Ψd=coth{[p1(t) +yd] [yd-p2(t) ]}.

当x1→-p1或x1→p2时，Ψ→±∞.因此，只要保证Ψ的有界性，输出x1一定保持在约束范围内.

对Ψ求导，得

注4 双曲余切函数cothx=coshx/sinhx和双曲余割函数cschx=1/sinhx为奇函数，在(-∞，0) 和(0，+∞)内单调递减.本文设计的状态变换函数需要满足：1）状态变换函数单调递减；2）当状态x1分别趋于下边界-p1和上边界p2时，p1(t) +x1→0+，x1-p2(t) →0-，状态变换函数Ψ→±∞.(cothx)'=-csch2x且cothx=±∞，因此将其用于状态变换函数的设计.

注5 与障碍Lyapunov 函数［20，22-23］解决输出约束问题相比，文献［20，22-23］研究的是对称输出约束.Meng 等［24］和Tran 等［25］虽然使用转换技术处理输出约束问题，但均把输出约束问题转化为输出误差约束问题.本文设计的非线性变换函数把输出约束问题转化为新状态的有界性问题，而且，此变换函数适用于时变、对称或非对称约束的情况.非线性函数式（3）可以选取为文献［24-25］中的非线性变换函数，但是文献［24-25］需要将输出约束问题转化为输出误差约束问题.此外，式（3）可以选取为文献［31-32］的分式型和双曲余切型状态变换函数，本文的状态变换函数进行求导时计算相对简单，计算量小一些.

2 有限时间控制策略设计

本节将基于反步法设计控制策略，控制系统框图如图1所示.

图1 控制系统框图Fig.1 The block diagram of control system

2.1 有限时间滤波器设计

为了避免反步设计的“计算爆炸”问题，设计有限时间滤波器，首先给出如下假设：

假设3 滤波器的输入信号的导数有界.

设计的有限时间滤波器如下：

式中：υi，ε，qi1，qi2，qi3，qi4为正常数；ξi1为滤波器的输出；ei=ξi1-αi为滤波误差.

定理1 在假设3 下，对于以上滤波器，存在δ=[(1-α)/α]＞0，α∈(1，min{[ρ/(ρ+2)，1/2]})，ρδ＞2，使得

式中：ο(ερδ-i+1)代表ξii-的逼近误差.

证明：构造以下非线性系统.

其中，q1，q2，q3，q4为正常数.

选取Lyapunov函数

对V0求导，可得：

由文献［9］可知，非线性系统（5）是有限时间稳定的.因为∀ψ，φ∈R，|arctanψ-arctanφ| ≤|ψ-φ|，所以

其中，q=max{q1，q2，q3，q4}.由文献［4］，定理1得证.

注6 文献［10-12，19］的滤波器只有线性部分或者非线性部分，可能会造成当滤波器状态靠近平衡点时收敛速度慢，远离平衡点时收敛速度快.本文设计的有限时间滤波器式（4），同时包含线性部分和非线性部分，可以保证滤波器状态无论靠近平衡点还是远离平衡点时都具有较快的收敛速度.

注7 由定理1可知α∈(0，1/2)，ρδ＞2，根据稳定性分析可知，|ei|≤ερδ-i+1lμδ，μ=2c-1Hv，l=[rc(1-θ)-1]＞0，H为利普希茨常数，v=+h2，h1，h2＞0，分别为虚拟控制输入信号的导数(dαi/dt)，(d2αi/dt2)的上界.当α的取值很小时，δ很大，根据ρδ＞2 可知ρ很小，则v=+h2和μ=2c-1Hv相对很小，因此lμδ很小.此外，选取尽可能小的ε使得滤波误差中ερδ-i+1更小.因此α，ε的取值越小越好.另外，根据稳定性分析可知，q=max{q1，q2，q3，q4}，其中q1=qi1/υi，q2=qi2/υi，q3=qi3/υi，q4=qi4/υi与H有关，选取较小的qi1，qi2，qi3，qi4以及较大的υi，可以使μ=2c-1Hδ的值相对较小.

2.2 自适应有限时间控制器设计

首先，定义如下误差变量：

其 中，Ψd=coth{[p1(t) +yd][yd-p2(t) ]}，αi，c=ξi1为有限时间滤波器的输出.

注8 本文结合Pade 近似法和坐标变换，消除了输入时延对控制效果的影响.zn=xn-αn-1，c+λ-1gn xn+1和实际控制器u对时延τ和引入的中间变量xn+1进行补偿，xn+1在反步设计的最后一步被消除.

为消除滤波误差ei的影响，引入补偿信号ri，定义误差补偿变量hi=zi-ri，i=1，2，…，n.

接下来，将基于反步控制法设计控制器.

Step 1：选取Lyapunov函数为

对V01求导，得

由杨氏不等式，得：

定义θ1=max{1，}，a1，b1，c1，d1＞0.

将式（9）代入式（8），得：

设计虚拟控制输入和补偿信号为：

选取Lyapunov函数为：

对V1求导，得：

基于式（14），设计自适应律为：

结合式（10），将式（11）、式（12）、式（15）代入式（14），得：

Stepi(2 ≤i≤n-1)：选取Lyapunov函数为：

对V0i求导，得：

由杨氏不等式，得：

定 义θi=max{1}，ai，bi，ci＞0.将 式（18）代入式（17），得：

设计虚拟控制输入和补偿信号为：

选取Lyapunov函数为：

对Vi求导，得：

基于式（23），设计自适应律为：

结合式（19），将式（20）、式（21）和式（24）代入式（23），得：

Stepn：选取Lyapunov函数为

对V0n求导，得：

由杨氏不等式，得：

定义θn=max{1}，an，dn＞0.将式（27）代入式（26），得：

设计虚拟控制输入和补偿信号为：

选取Lyapunov函数为：

对Vn求导，得：

基于式（32），设计自适应律为：

结合式（28），将式（29）、式（30）和式（33）代入式（32），得：

3 稳定性分析

闭环系统的稳定性可总结为如下定理：

定理2 对于非线性系统（1），若满足假设1～假设3，则在控制律式（29），自适应律式（15）、式（24）、式（33）的作用下，闭环系统实际有限时间稳定；输出满足约束且输出误差在有限时间T内收敛到关于零的任意小邻域.其中，

t0为系统运行的初始时刻.

证明：基于式（34）、引理2、定理1 和杨氏不等式，可得

其中，|gi(⋅)| ＜Λi2＞0，mi＞0.

将式（35）～ 式（37）代入式（34），得：

其中，χ=[χi，，ri]，i=1，2，…，n.

令a0=min{a01，a02}；b0=min{b01，b02}；w0=max{w01，w02}，则

由闭环系统的实际有限时间稳定可知，hi，，ri有界，因此z1=h1+r1有界.由yd有界可知Ψd有界，所以Ψ=Ψd+z1有界.从而x1保持在约束范围内，即-p1(t) ＜x1＜p2(t).

注9 计算稳定时间T涉及的参数有：t0，a0，a，b0，w0，p，其中，t0=0，a0=min{a01，a02}，0 ＜a＜a0，b0=min{b01，b02}，w0=max{w01，w02}，1/2 ＜p＜1.根据稳定性分析中a01，a02，b01，b02，w01，w02的表达式可知，参数k11，kn1，li，σi1，σi2＞0，i=1，2，…，n.另 外，ki1＞ki1＞0.5，i=2，…，n-1；ki2＞1/(2p)，σi1＞σi2p，i=1，2，…，n.结合p的取值范围进一步可知，ki2＞1，σi1＞σi2.因此，在保证闭环系统稳定性的前提下，可以恰当选取计算有限时间所涉及的参数.

注10 文献［7-8］未考虑一阶滤波器的滤波误差影响.本文设计补偿机制，消除了滤波误差的影响.

注11 由η的表达式可知，当x1=(p2-p1)/2 时，η=0.采取如下两种方法解决此问题：1）设系统运行时输出x1的真实约束为-p01(t) ≤x1≤p02(t)，p01(t)，p02(t) ＞0（可由输出的参考指令确定大概的范围），只要(p2-p1)/2 ＜-p01或(p2-p1)/2 ＞p02时，可以保证η≠0，即p2＜p1-2p01且p1＞2p01或者p2＞2p02+p1且p1＞p01；2）当x1=(p2-p1)/2 时，令η=ε0，ε0为远小于1的正常数.

注12 文献［25］考虑了约束非线性系统的有限时间控制问题.文献［27-28］研究了具有输出约束和输入时延的非线性系统控制问题.但是二者都将输出约束转化为输出误差约束问题.本文同时考虑输出约束和输入时延，设计只与输出有关的非线性变换函数，保证输出满足约束，并提出有限时间反步控制策略.

注13 根据文献［33］可知，Pade 近似法适用于时变时延情形.本文中，若考虑时变时延，首先需要假设输入时延τ及其导数有界，则存在γ＞0，使得|λ-1|＜γ.在控制器的设计过程中，误差补偿机制以及前n-1 步的虚拟控制输入、自适应律与常数时延情形相同.不同之处在于第n步控制输入和自适应律中Φn的表达式不同.时变时延时，Φn=类似于常值时延时闭环系统的稳定性分析，可得时变时延下，由引理1 可知，闭环系统是实际有限时间稳定的.

4 仿真分析

为了验证所设计的有限时间滤波器式（4）和控制策略的有效性，将本文滤波器式（4）与有限时间滤波器［19］以及一阶滤波器做对比仿真.然后，将设计的控制策略应用于机械臂系统控制的仿真.

4.1 滤波器的对比仿真

将有限时间滤波器式（4）与一阶滤波器［7-8］及有限时间滤波器［19］做对比，选取如下两种滤波输入信号：情形1，αi=1；情形2，αi=sint+sin(0.5t).

在相同的初值条件和参数下进行仿真，选取滤波器参数为：υi=0.1，ε=0.01，q11=q12=q13=500，q14=50.图2、图3为滤波器的对比结果.

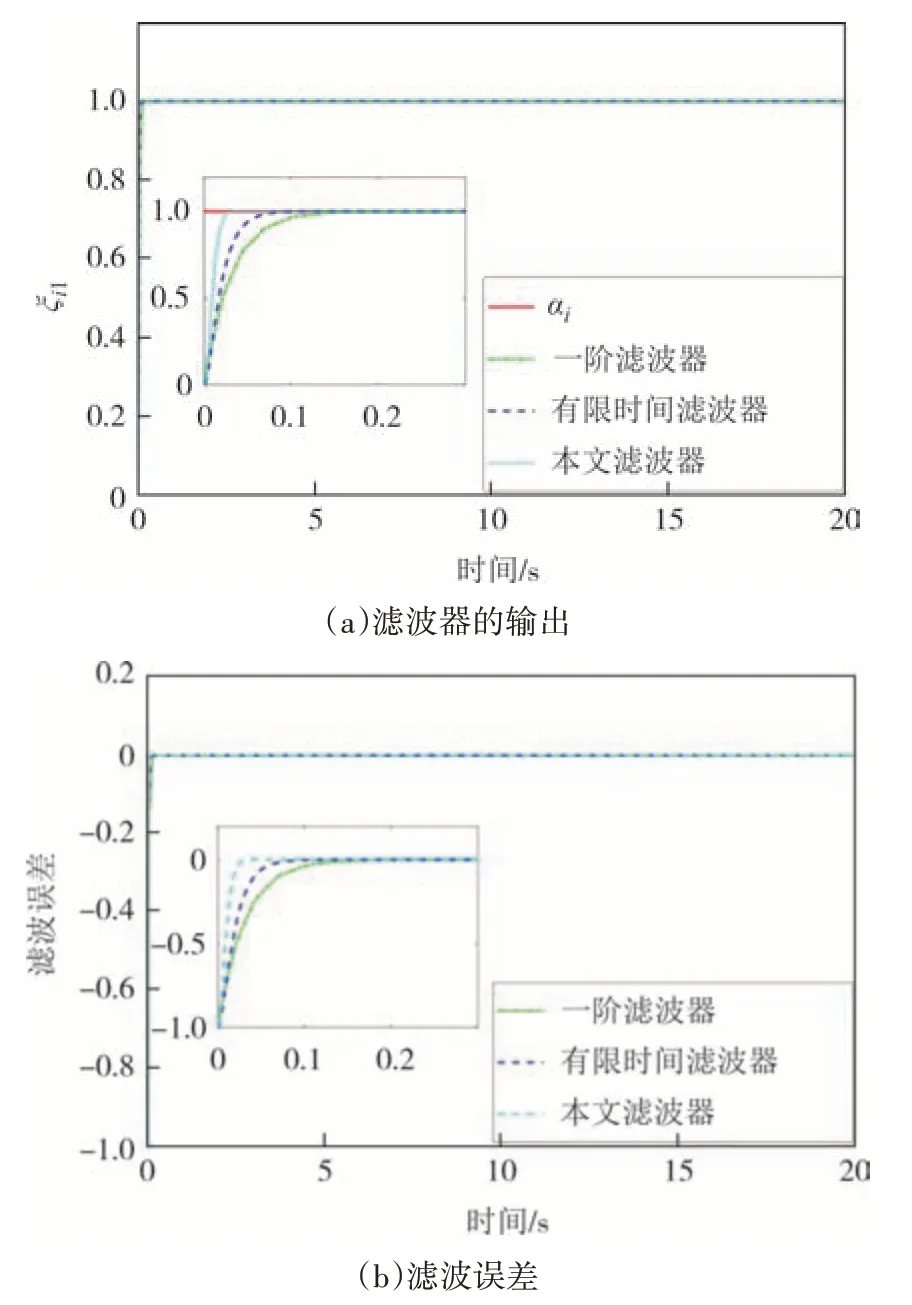
图2 情形1的对比结果Fig.2 The comparison results of case 1

图3 情形2的对比结果Fig.3 The comparison results of case 2

如图2、图3 所示，本文的有限时间滤波器在两种情形下，均具有最快的收敛速度和较好的估计精度.具体地，由图2 可知，情形1 中，一阶滤波器的估计误差在0.19 s 收敛.有限时间滤波器作用下，估计误差在0.14 s 收敛.而本文的有限时间滤波器式（4）的估计误差在0.05 s 收敛.由图3 可知，三种滤波器作用下，本文有限时间滤波器式（4）的估计误差精度最高.

4.2 机械臂系统应用仿真

为了验证设计的控制策略的有效性，进行如下的单链机械臂系统的仿真：

其中，q、分别代表连杆的角位置、角速度和角加速度，m为连杆质量，L为连杆长度，g=9.8 m/s2为重力加速度，u为连杆的控制扭矩.

考虑输入时延，令x1=q，x2=，上述系统转化为：

在相同的初值条件和控制器参数下进行以下两种情形的对比仿真：

情形1：常值输入时延τ=0.05 s；

情形2：时变输入时延τ=[0.015+0.002sin(3t)]s.

仿真中，机械臂参数选取为：M=1 g⋅m-2，m=2 kg，L=0.1 m 且考虑连杆长度10%的不确定.参考指令yd=[0.28cos(0.5t)]+0.2 m，非对称输出约束函数 为p1(t)=[1.1+0.3sin(2t)] m，p2(t)=[0.69 +0.13sint] m.初值选取为：x1(0)=-0.09，x2(0)=0.01，x3(0)=0；(0)=(0)=0.05.滤波器参数选取 为：ε=0.6，ν1=0.36，q11=105，q12=70，q13=0.052，q14=1.45.控制器参数选取为p=0.8，k11=1.52，k12=2.34，k21=0.75，k22=5.35，σ11=2.15，σ12=2.1，σ21=2.5，σ22=2.01，l1=0.01，l2=0.23.结合计算有限时间所涉及的参数可得，a0=0.695，b0=0.006 25.常值时延时，Vn[χ(t0) ]=1.28，w0=52.11；时变时延时，Vn[χ(t0) ]=1.289 3，w0=64.62.令a=0.5 ＜a0，计算可得常值时延时，稳定时间T≤8.6 s；时变时延时，稳定时间T≤9.008 s.

仿真结果如图4、图5所示.图4为输出和跟踪误差的变化曲线，可以看出两种情形下，输出在8.6 s和9.008 s 内实现对参考指令yd的跟踪，且始终保持在约束范围内，跟踪误差收敛到零附近的小邻域.图5为状态x2和误差z1的变化曲线，由图5 可知，z1收敛到零附近的小邻域.图6 为和u的变化曲线，能够看出参数估计误差收敛到零附近的小邻域.根据以上分析可知，Pade 近似法既适用于常值时延的情形，也适用于时变时延的情形，本文设计的控制策略在两种情形下均可以实现较好的性能.从仿真结果可以看出，常值时延下跟踪精度优于时变时延，时变时延下，相比常值时延，控制输入的变化更慢.

图4 输出和跟踪误差的变化曲线Fig.4 The curve of output and tracking error

图5 x2和z1的变化曲线Fig.5 The curve of x2 and z1

图6 和u的变化曲线Fig.6 The curve of and u

5 结论

本文研究了输入时延和输出约束影响下的不确定非线性系统的控制问题.首先构造新的非线性变换函数保证输出不违反约束，设计了有限时间滤波器解决了“计算爆炸”问题.同时，设计了补偿机制消除滤波误差.基于此，设计了自适应反步有限时间控制策略.接着，利用Lyapunov理论证明了闭环系统的有限时间稳定性.最后，滤波器的对比仿真和机械臂系统的控制仿真体现了滤波器的优越性和控制策略的有效性.Pade 近似法只适用于短时延的情形，因此，未来将讨论长时延影响下不确定非线性系统的控制问题.