热环境下弹性地基上多孔FGM 圆板的自由振动特性

滕兆春 ，王伟斌，薛刚

（兰州理工大学 理学院，甘肃 兰州 730050）

功能梯度材料（Functionally Graded Materials，FGM）是一种新型的非均匀复合材料，其作为智能化材料的典型代表，在工程领域内应用广泛［1］.随着新型材料的兴起，FGM 圆板/环板作为核工业、航天、机械和土木等工程中常见的重要功能结构元件，在工程实际中具有较多的应用背景，尤其是应用于高温工况中.为了准确评估FGM 结构的机械行为和为工程设计提供理论依据，许多学者先后展开了大量的研究工作.

目前，关于FGM 圆板结构的力学行为研究已有较多的研究成果，具体可参考Boutahar 等［2］、Allahverdizadeh 等［3］、Ma 等［4］和李世荣等［5］诸多学者的系列研究工作.近年来，许多研究者对FGM 圆板/环板结构的静动态响应分析，如屈曲和振动方面做了大量的工作，可见文献［6-7］.由于FGM 圆板/环板是大多数结构的关键元件，以下文献集中利用不同理论和不同方法对FGM圆板/环板力学行为进行研究.如Hosseini-Hashemi 等［8］基于一阶剪切变形Mindlin 理论，给出了阶梯厚度圆形和环形功能梯度板自由振动的精确解.利用分离变量法求解了其自由振动，研究了FGM 板的几何参数和材料参数，如阶梯厚度比、阶梯位置和梯度指数对固有频率的影响.Asemi等［9］首次采用三维弹性理论，研究了FGM 环形、扇形板的剪切屈曲问题，详细研究了载荷、边界条件、梯度指数和扇形角等对FGM 环形、扇形板剪切屈曲载荷和振型的影响.Malekzadeh 等［10］基于三维弹性理论，研究了热环境下FGM 厚环板的自由振动分析，应用微分求积法（DQM）求解了热弹性平衡方程和自由振动方程，研究了温升、材料和几何参数对固有频率的影响.Tajeddini 等［11］基于线性、小应变和精确弹性理论，分析了Pasternak 地基上径向变厚度的厚各向同性材料和FGM 圆形及环形板的三维自由振动问题，并利用多项式Ritz法求解了特征值问题.

在此研究基础上，考虑到FGM 构件的实际应用背景和材料自身情况，如FGM 微纳米器件和多孔FGM 等，许多研究者相继将微观理论和多孔材料特性等应用于FGM 圆板开展研究，如Goodarzi 等［12］利用修正应变梯度理论（MSGT）和修正偶应力理论（MCST），研究了黏弹性地基上圆形和环形纳米板的热-机振动问题，使用微分求积法（DQM）和伽辽金法求解控制方程，研究了尺寸相关、平面预紧力、温度变化和弹性介质等因素对固有频率的影响.Eshraghi等［13］给出了统一表示的位移场，基于修正的偶应力理论介绍了热载FGM 环形和圆形微板的静力弯曲和自由振动问题的求解方法，分析了热载荷、材料和几何参数对静态变形、应力和自振频率的影响.Jabbari 等［14］研究了具有压电驱动器层的多孔材料径向实心圆板的热屈曲，利用变分得到了压电多孔板的控制方程，给出了圆板在温度载荷作用下的封闭解，分析了多孔板厚度、孔分布、压电厚度、外加驱动电压和孔隙率变化对临界温度载荷的影响.Behravan等［15］基于三维弹性理论，分析了受非均匀面力和非对称Kerr 弹性地基上非轴对称变厚度FGM 多孔圆板的磁-弹问题，基于径向和厚度方向上的微分求积和状态空间矢量技术，讨论了面力、边界条件和弹性地基对位移、应力、电磁应力和磁扰动量的影响.Rahmani 等［16］通过考虑两种类型的孔隙率分布，首次应用修正的高阶夹层板理论，使用伽辽金法研究了两种多孔FGM圆形夹层板的振动特性.

综上所述，已有关于FGM 圆板的文献表明，对多孔FGM 圆板的研究则相对较少，同时一些研究结果也很好地验证了微分变换法（Differential Transformation Method，DTM）在求解特征值问题时的实用性和有效性［17］.目前关于热环境下弹性地基上多孔FGM 圆板自由振动问题的研究在国内外还鲜见有文献报道，因此本文考虑均匀分布孔隙引入力学模型，采用DTM 对不同温度场中多孔FGM 圆板自由振动展开研究，分析梯度指数、孔隙率、升温、边界条件、厚度与半径比和弹性地基系数等对多孔FGM 圆板无量纲固有频率以及相关各参数对临界温升值的影响，为今后多孔FGM圆板的研究提供数据支撑.

1 多孔FGM 圆板的物性参数

1.1 材料物性描述

如图1（a）所示，选取柱坐标(r，θ，z)分别表示径向、环向和横向坐标，建立弹性地基上多孔FGM 圆板的力学模型.多孔FGM 圆板半径为R，厚度为h，kw为Winkler 弹性刚度系数，上表面为纯陶瓷，下表面为纯金属，含均匀孔隙FGM 各物性参数P(z，T)（弹性模量E、密度ρ和热膨胀系数α）可用改进的混合幂律公式表示［18］：

图1 弹性地基上多孔FGM圆板的几何模型和横截面上均匀分布的孔隙Fig.1 Geometric model of porous FGM circular plate on elastic foundation and uniformly distributed pores in cross section

式中：n为梯度指数；Pc、Pm分别表示无孔隙时陶瓷和金属材料的物性参数；β为孔隙率，均匀分布的孔隙如图1（b）所示.

上述金属和陶瓷的某一物性参数P随温度T的变化可采用 Touloukian 非线性函数［19］统一表述为：

式中：P0、P-1、P1、P2和P3为温度相关的系数，一般由实验给出，见表4.

1.2 温度场描述

在不考虑材料导热率情况下，本文给出一种统一的温度场表达式，可以更好地描述温度场

式中：ΔT=Tc-Tm表示多孔FGM 圆板上下表面温度差，Tc和Tm分别为上下表面温度值；η为温度指数.当Tm=T0=300 K时，表示无应力状态的参考温度，此时当η=0 时为均匀升温，当η=1 时为线性升温，当η取其他值时均为非线性升温.

将式（2）、式（3）代入式（1），即可得到不同孔隙率下多孔FGM圆板的物性参数.

2 控制微分方程的推导与DTM变换

2.1 无量纲控制微分方程

基于小挠度假设和一阶剪切变形理论，多孔FGM圆板的位移分量如下：

式中：ur、uθ和uz分别表示圆板径向、环向和横向位移；φ为法线的转角；w为横向位移；t为时间；z0为物理中面.物理中面内应力分量与应变分量为零，其表达式如下［20］：

圆板考虑轴对称，其几何方程为：

式中：εr、εθ和γrz分别表示径向应变、环向应变和切应变.物理方程为

式中：σr，σθ和τrz分别表示径向应力、环向应力和切应力；ν为泊松比；T0表示无应力状态的参考温度，本文取T0=300 K.

多孔FGM 圆板单位面积的薄膜力和弯矩分别为：

式中：B、C、D为刚度系数；κs为剪切修正系数，且取κs=π212；NT和MT分别为热轴力和热弯矩，可定义为

应用Hamilton 变分原理可推导出热环境下弹性地基上多孔FGM 圆板的自由振动问题的控制微分方程.Hamilton原理如下：

式中：Π 为Hamilton 作用量；S、U和V分别为系统的动能、应变能和外力做的功；δ为变分符号；t1和t2分别表示系统运动的初始时刻和终止时刻.

可得多孔FGM圆板的动能的变分为：

惯性系数为：

其中，

多孔FGM圆板的应变能的变分为：

多孔FGM圆板的外力做功的变分为：

式中：kw为Winkler弹性刚度系数.利用上述Hamilton原理，可得到多孔FGM 圆板的热环境下弹性地基上多孔FGM圆板自由振动的控制微分方程.

将式（8）～式（12）代入式（17）和式（18），并假设多孔FGM 圆板做简谐振动，令w(r，t)=wˉ(r)cosωt，φ(r，t)=-φ(r)cosωt，其中ω是多孔FGM圆板的固有频率，wˉ(r)和-φ(r)是形状函数.代入式（17）、式（18），可以得到多孔FGM圆板的运动控制微分方程为：

引入如下无量纲参数：

式中：λ为厚度与半径比；Kw为无量纲Winkler 弹性刚度系数为无量纲热载荷；Ω为无量纲固有频率.

综上可得到热环境下弹性地基上多孔FGM 圆板自由振动的无量纲控制微分方程

对于热环境下弹性地基上多孔FGM 圆板自由振动问题，本文考虑了两种边界条件，其形式如下：

ξ=0，圆板中心边界为：

2.2 DTM变换

对于热环境下弹性地基上多孔FGM 圆板自由振动的无量纲控制微分方程组（20）、（21）的特征值问题，这里采用一种半解析方法——微分变换法（DTM）进行求解.该方法在求解特征值问题时具有过程简单、编程方便的特点，且对于特征值无需经逆变换过程即可得到［17，21］.按照DTM的求解过程及原理［22］，将其无量纲控制微分方程组转换为如下的迭代代数方程组可表示为：

边界条件的DTM变换如下：

ξ=0，圆板中心边界为：

3 算例分析与数值讨论

应用MATLAB 软件编写相关程序，由此可得到通过DTM 求解多孔FGM 圆板自由振动时的无量纲固有频率.为了验证DTM 的正确性，不考虑材料受温度依赖，经算例1 退化为孔隙率为零时的FGM 圆板，得到表1、表2 和表3 结果，并与文献［23］和［24］中的结果进行比较.考虑材料受温度依赖，经算例2得到图2～图9新的结果.

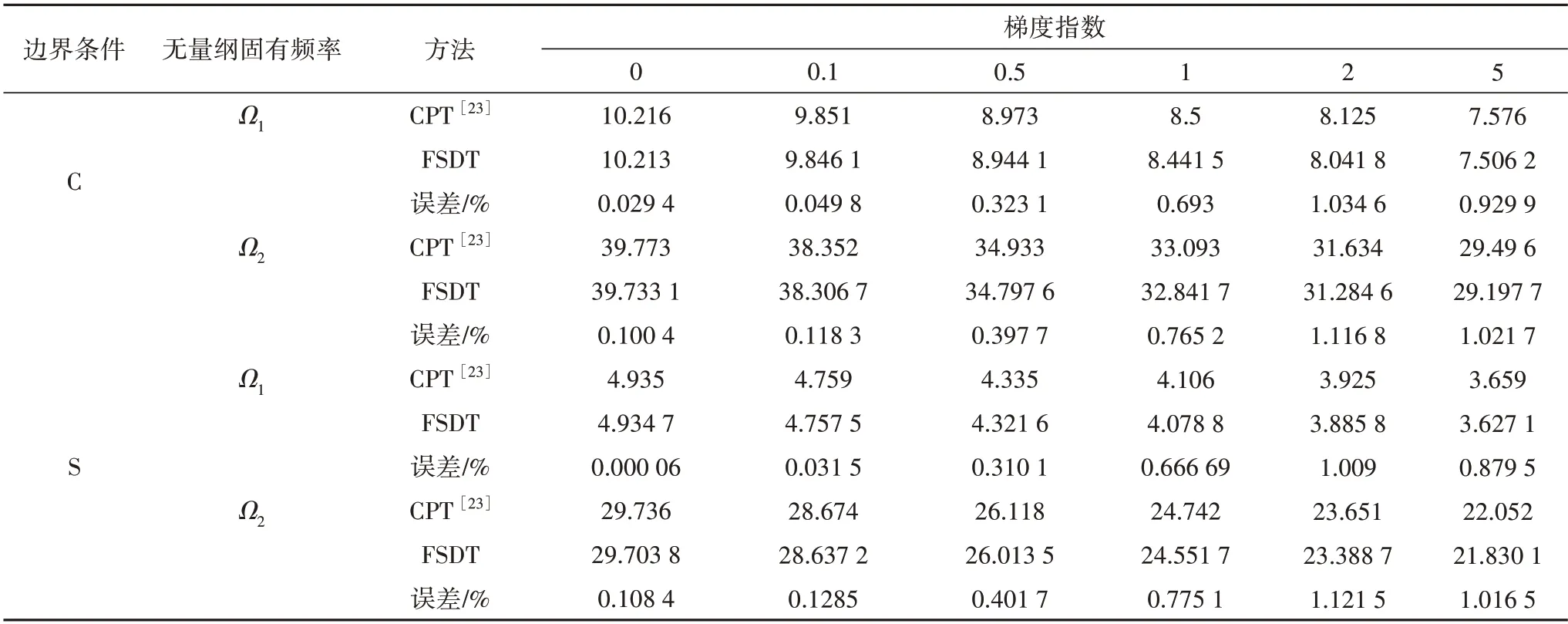
表1 固支和简支边界条件下一阶剪切变形理论和经典板理论的无量纲固有频率对比（λ=0.01）Tab.1 Comparison of dimensionless natural frequencies between first-order shear deformation theory and classical plate theory under C and S boundary conditions（λ=0.01）

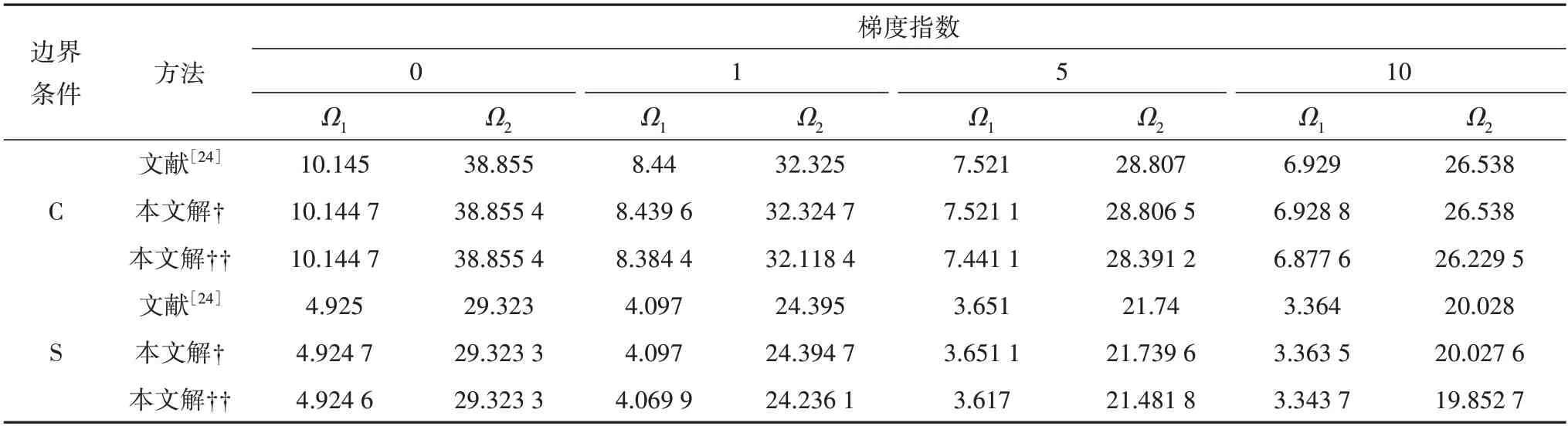
表2 固支和简支边界条件下不同梯度指数对FGM 圆板无量纲固有频率的影响（λ=0.05）Tab.2 Effects of different gradient indices on the dimensionless natural frequencies of FGM circular plates under C and S boundary conditions（λ=0.05）

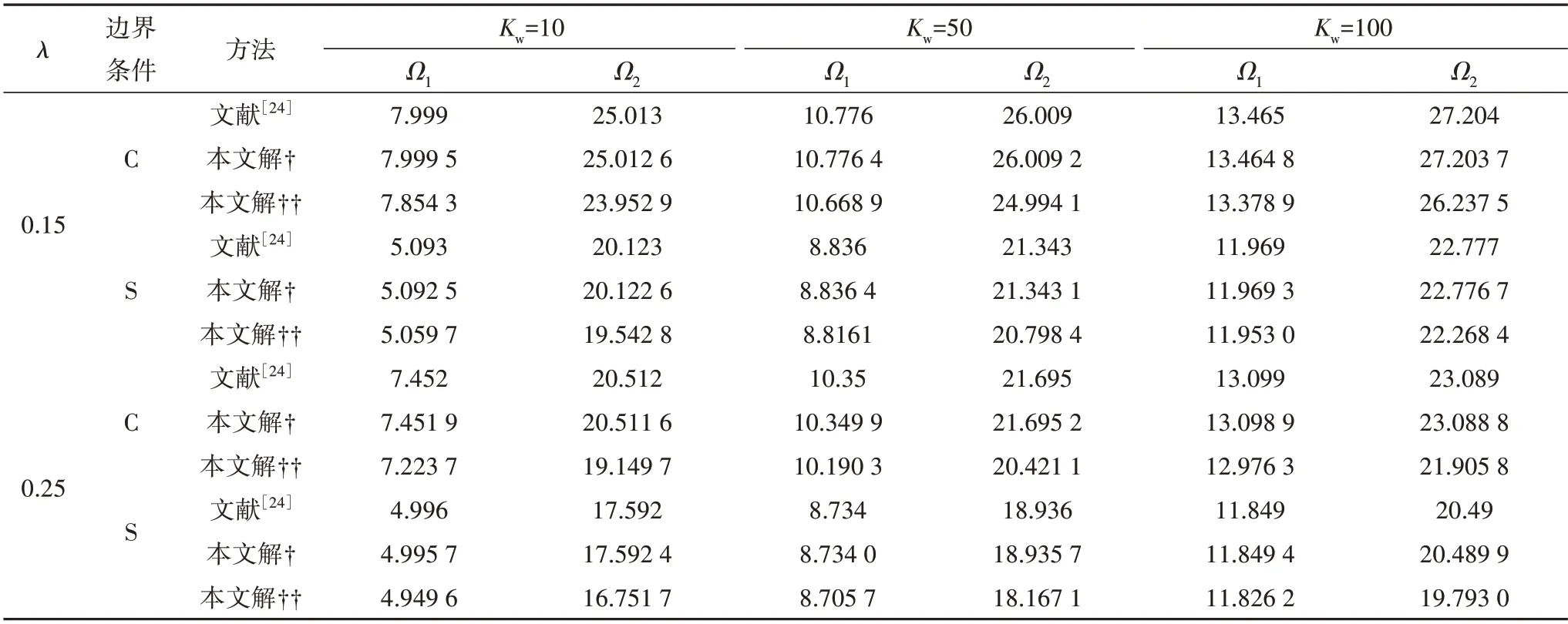
表3 固支和简支边界条件下不同Winkler系数对FGM 圆板无量纲固有频率的影响Tab.3 Effect of different Winkler parameter on the dimensionless natural frequency of FGM circular plate under C and S boundary conditions

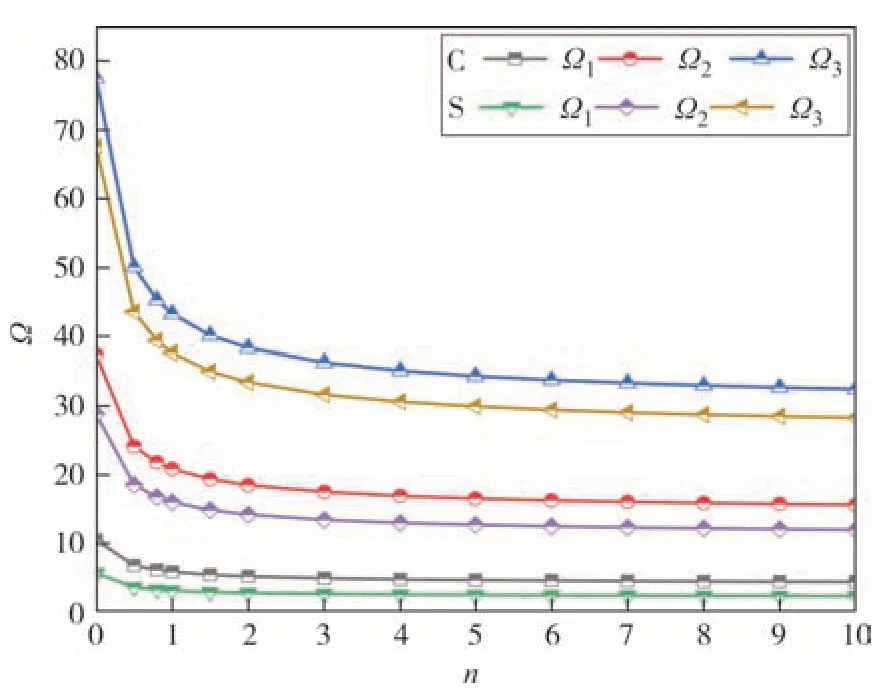
图2 均匀升温下梯度指数对无量纲前三阶固有频率的影响曲线Fig.2 The influence curve of gradient index on the first three dimensionless natural frequencies under uniform temperature rise

算例1：表1 给出了在固支（C）和简支（S）边界条件下，FGM 圆板取不同梯度指数时，基于经典板理论（CPT）的前两阶固有频率［23］与本文基于一阶剪切变形理论（FSDT）的DTM 解对比，发现DTM 求出的解与文献解在准确性和精度上完全吻合.其中取ρc=3 800 kg/m3，ρm=2 700 kg/m3，Ec=380 GPa，Em=70 GPa，ν=0.3，λ=0.01，β=0.

表2 和表3 为固支（C）和简支（S）边界条件下，不同梯度指数和Winkler 系数下，基于一阶剪切变形理论（FSDT）得到FGM 圆板和弹性地基上FGM圆板振动的无量纲前两阶固有频率，若依据文献［24］对刚度无量纲过程处理方法，得到本文解†与之对照，发现其数值结果完全吻合.本文在刚度无量纲过程中与文献［24］不同，引入了物理中面，虽然文中拉-弯耦合刚度为零，但对结构的耦合影响被带入弯曲刚度D和惯性刚度I2中，所以得到本文解††与表3 中无量纲前两阶固有频率略有差别，但也进一步证明了DTM 的精度满足要求，其中取ρc=3 800 kg/m3，ρm=2 702 kg/m3，Ec=380 GPa，Em=70 GPa，ν=0.3，β=0.

算例2：图2～图9 中各物性参数均遵循表4 中的实验数据，由于泊松比的取值对振动频率几乎没有影响，故在此ν取常数.

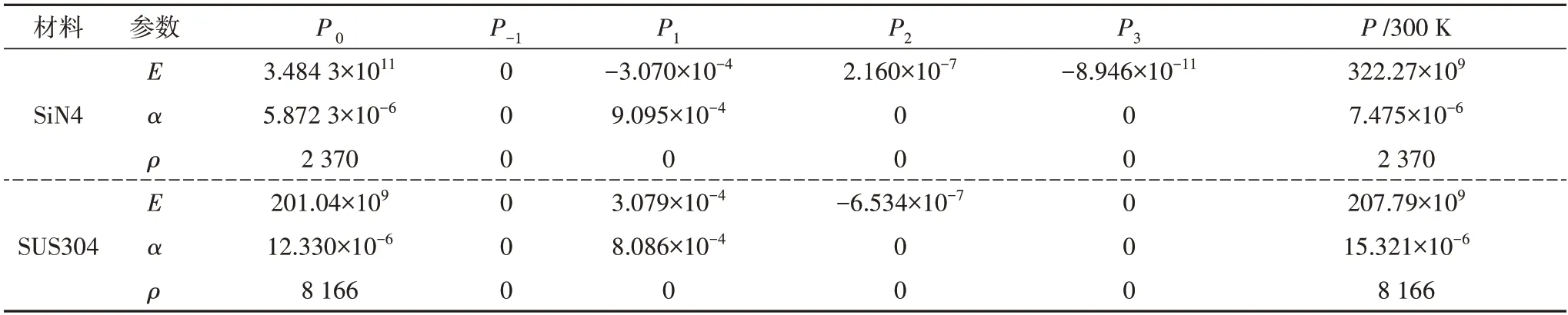
表4 陶瓷和金属材料物性参数的温度相关系数［19］Tab.4 Temperature correlation coefficient of physical parameters of ceramic and metal materials

图2 和图3 为多孔FGM 圆板在固支（C）和简支（S）边界下，当β=0.1，λ=1，Kw=10，ΔT=100 K时，不同梯度指数对无量纲前三阶固有频率Ω的影响曲线.可以看出在温度指数一定时，随着梯度指数n的增加，多孔FGM 圆板的无量纲固有频率Ω逐渐下降，当n在小值范围取值时（1 附近），无量纲固有频率Ω（减小的）波动很剧烈；当n在较大值范围取值时，无量纲固有频率变化趋于平缓.合理解释了FGM中陶瓷材料向金属材料过渡的特性.温度指数的变化表示升温类型的变化，均匀升温（η=0）和线性升温（η=1）类型下，梯度指数对固有频率的影响趋势基本一致，当梯度指数n一定时，随着温度指数η增大，无量纲固有频率在增大，边界约束越强，无量纲固有频率越大.

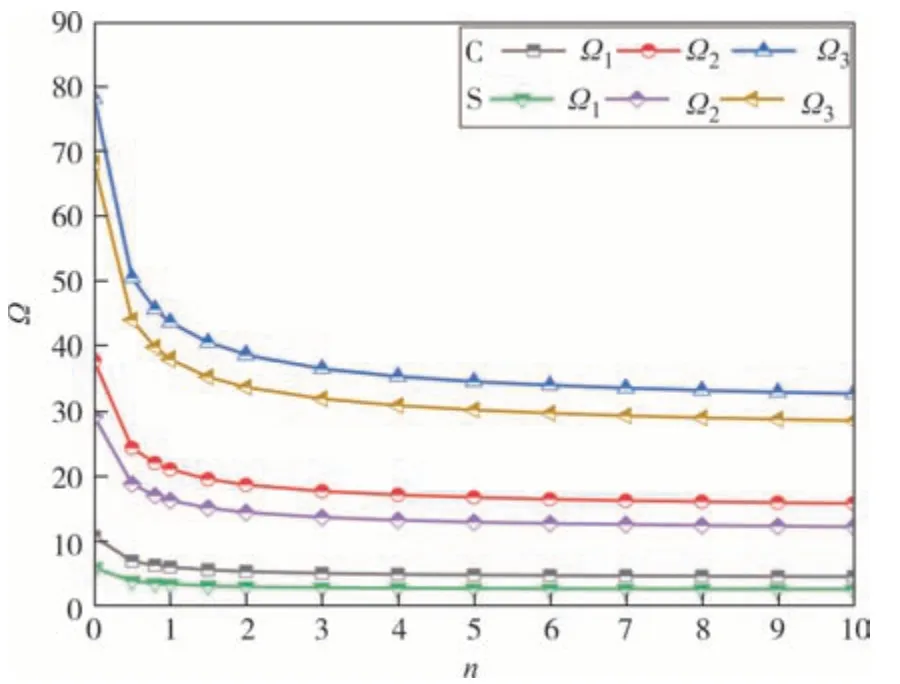
图3 线性升温下梯度指数对无量纲前三阶固有频率的影响曲线Fig.3 The influence curve of gradient index on the first three dimensionless natural frequencies under linear temperature rise

图4为多孔FGM 圆板在固支（C）和简支（S）边界下，当β=0.1，n=1，Kw=10，ΔT=100 K时，不同温度指数和厚度与半径比λ对无量固有纲频率Ω的影响曲线.可以看出随着厚度与半径比λ的增大，多孔FGM圆板的无量纲固有频率Ω在非线性单调减小，λ的取值在0.15～0.35 之间，C 边界下一阶固有频率减小的速度较快，S 边界下减小得较缓慢，而两种边界下二阶固有频率减小的速度均较快.当厚度与半径比λ一定时，随着温度指数η增大，无量纲固有频率增大，边界约束越强，无量纲频率越大.

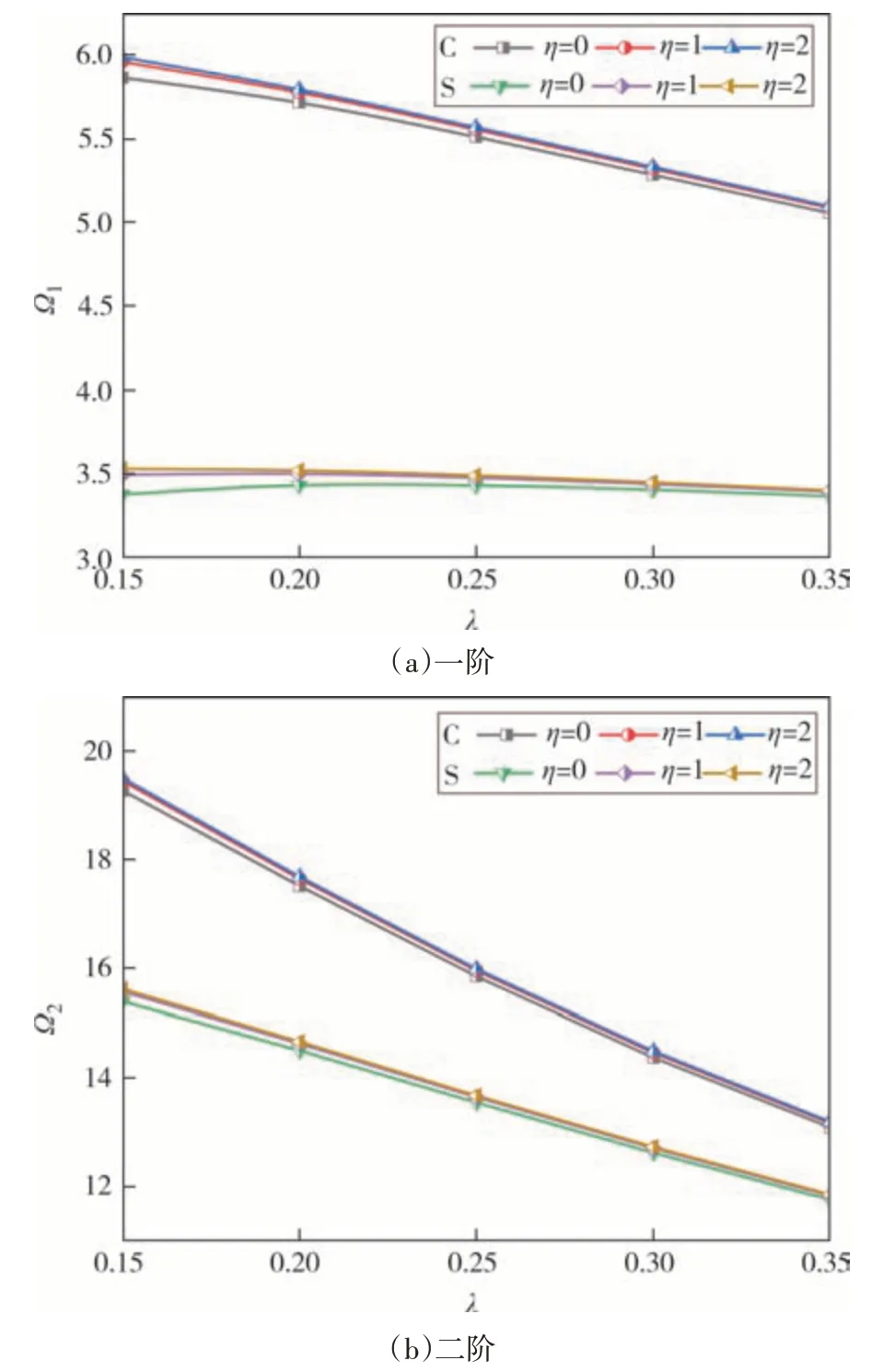
图4 不同厚度与半径比，不同温度指数对无量纲前两阶固有频率的影响曲线Fig.4 The influence curve of different thickness-to-diameter ratio and different temperature index on the first two order dimensionless natural frequencies

图5为多孔FGM 圆板在固支（C）和简支（S）边界下，当β=0.1，n=1，Kw=0，λ=0.1和不同温度指数时，温升值对无量纲基频Ω1的影响曲线.由结构稳定性理论［25］可知，当结构自振基频为零时，意味着结构构件发生失稳，所加载荷为最危险载荷即临界屈曲载荷，此时对应的温度即为临界屈曲温度.由图5可见，随着温升值的增加，多孔FGM 圆板的无量纲频率逐渐下降，具体表现在无量纲基频Ω1均随温升值的增大而减小，由于材料受温度依赖性温度300 K ≤T≤1 100 K［26］，当温升值取800 K 以内时，η=0 时，表示均匀升温下，无量纲基频Ω1减小至临界升温ΔTcr（或临界屈曲温度Tcr=T0+ΔTcr），（C 边界下，ΔTcr=679 K，S 边界下，ΔTcr=278 K），结构发生热屈曲而失稳，此时达到临界平衡状态，即Ω=0.当η=1时，表示线性升温，S边界同样减小至临界升温，此时ΔTcr=490 K，发生热屈曲，C 边界只有减小的趋势.同样，边界约束越弱，达到临界热屈曲时的温升值越小.

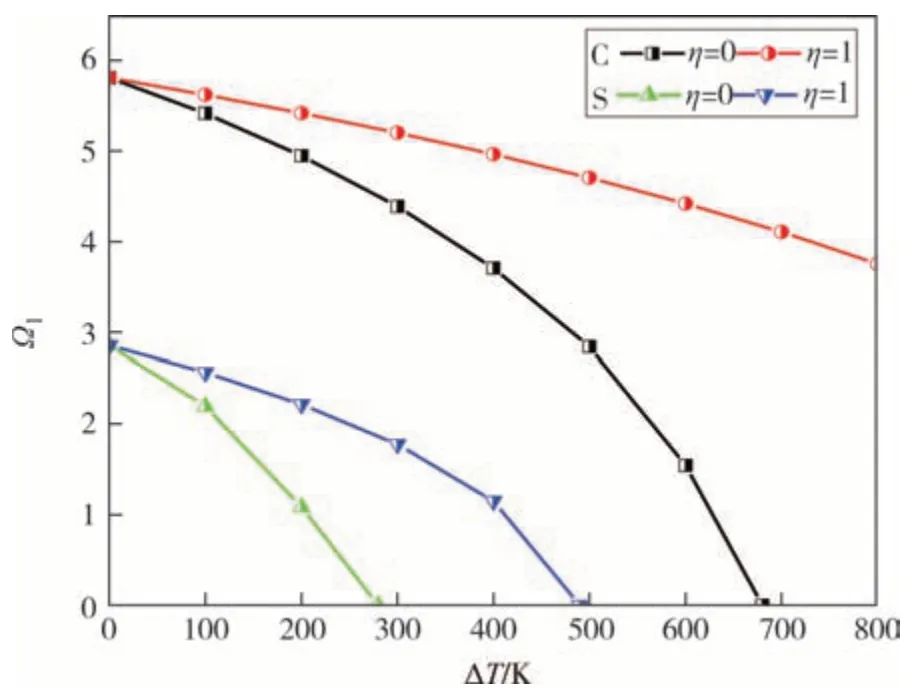
图5 不同升温类型对无量纲基频的影响曲线Fig.5 The influence curve of different heating types on dimensionless fundamental frequency

图6 和图7 反映了固支（C）和简支（S）边界和不同升温类型下，当ΔT=100 K，n=1，β=0.1，λ=0.1时，孔隙率β对多孔FGM 圆板无量纲前两阶固有频率Ω的影响曲线.图中显示：均匀升温（η=0）和线性升温（η=1）类型下，孔隙率β对无量纲固有频率Ω的影响趋势基本一致，当升温类型和温升值一定时，随着孔隙率β的增大，多孔FGM 圆板的无量纲固有频率逐渐上升，是因为孔隙的存在不仅削弱了FGM圆板的整体刚度，同时也降低了等效质量，此时质量的弱化强于刚度弱化.当孔隙率β一定时，随着温升值增大，无量纲固有频率减小，边界约束越弱，无量纲固有频率越小.

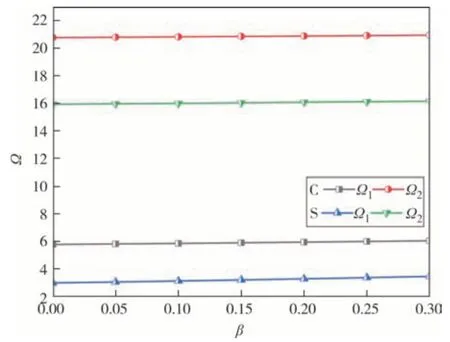
图6 均匀升温下孔隙率对无量纲前两阶固有频率的影响曲线Fig.6 The influence curve of porosity on the first two dimensionless natural frequencies under uniform temperature rise

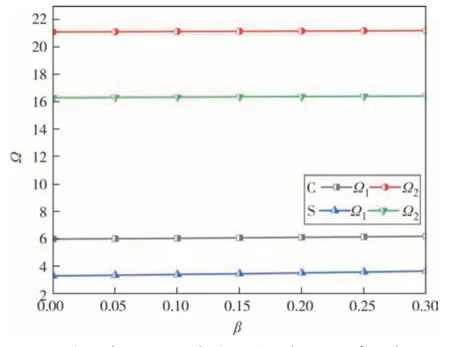
图7 线性升温下孔隙率对无量纲前两阶固有频率的影响曲线Fig.7 The influence curve of porosity on the first two dimensionless natural frequencies under linear temperature rise

图8 和图9 给出了在固支（C）和简支（S）边界条件下，当ΔT=100 K，n=1，β=0.1，λ=0.1 时，无量纲Winkler 弹性刚度系数Kw对无量纲固有频率Ω的影响.结果表明：当无量纲弹性刚度系数增大时，无量纲固有频率增大，且无量纲二阶固有频率几乎呈线性变化.当刚度系数增大时，增强了结构的整体刚度，且当弹性刚度系数Kw一定时，边界约束越强，无量纲固有频率越大.

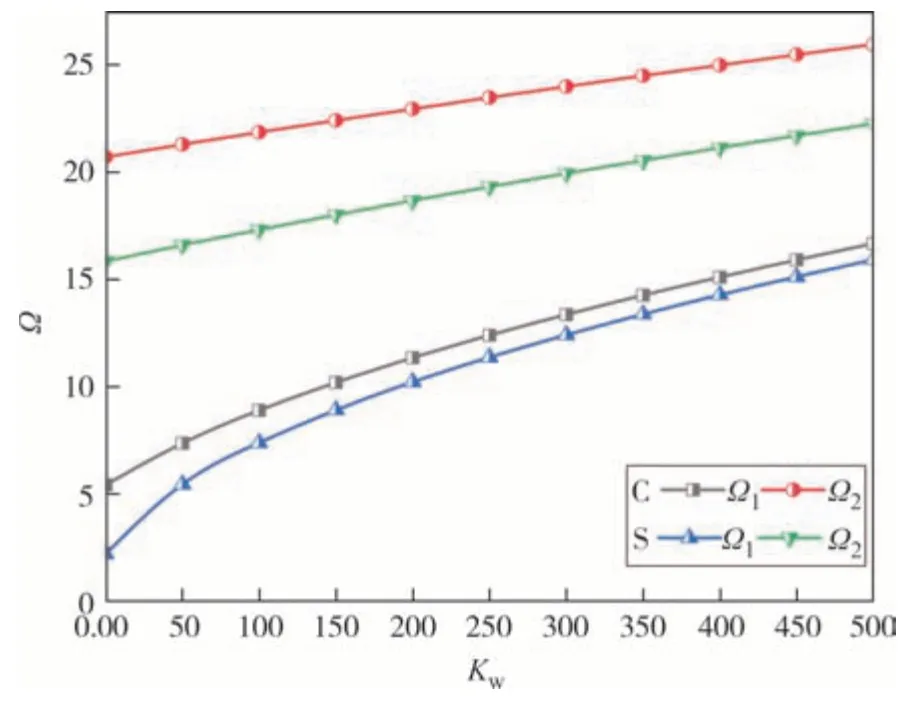
图8 均匀升温下无量纲Winkler弹性刚度系数对无量纲前两阶固有频率的影响曲线Fig.8 The influence curve of dimensionless Winkler elastic stiffness coefficient on the first two dimensionless natural frequencies under uniform temperature rise

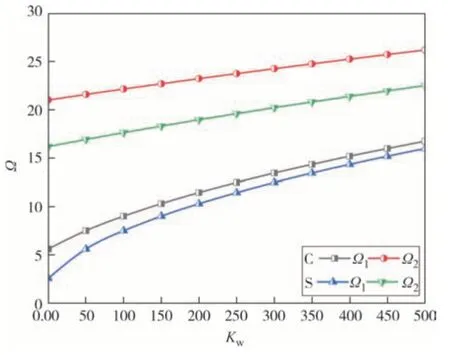
图9 线性升温下无量纲Winkler弹性刚度系数对无量纲前两阶固有频率的影响曲线Fig.9 The influence curve of dimensionless Winkler elastic stiffness coefficient on the first two dimensionless natural frequencies under linear temperature rise

4 结论

本文基于一阶剪切变形理论，考虑修正的混合幂律多孔FGM 圆板模型，在统一温度场下应用Hamilton 原理导出该热环境下该结构自由振动的控制微分方程，使用微分变换法（DTM）对自由振动和屈曲的运动控制微分方程及边界条件进行变换，通过编写MATLAB 程序计算多孔FGM 圆板的无量纲固有频率和临界温升值，并且与已有文献对比以验证结果的正确性.分析了不同边界、孔隙率、梯度指数、温度指数、厚度与半径比、温升值和Winkler 弹性刚度系数对多孔FGM 圆板无量纲固有频率的影响和相关参数各对临界温升值的影响.主要结论如下：

1）无量纲固有频率随着梯度指数n的增大而减小，随着梯度指数n趋向于无穷大，无量纲固有频率趋于不变，合理地解释了FGM 中陶瓷材料向金属材料过渡的特性.

2）随着厚度与半径比的增大，无量纲固有频率减小，随升温类型η值的增大，无量纲固有频率增大.

3）无量纲固有频率随着孔隙率β增大而增大，因为存在孔隙，降低了多孔FGM 圆板的整体刚度和有效质量，而对质量的弱化强于刚度弱化的原因导致了这一结果.

4）随温升值的增大，无量纲固有频率减小，减小直至发生热屈曲而失稳，使得无量纲基频变为零，此时达到临界平衡状态.

5）无量纲Winkler 弹性刚度系数Kw越大，无量纲固有频率Ω越大，且二阶固有频率几乎呈线性变化.