基于GAMLSS-GLO及随机森林算法的土石坝渗流监测模型

2023-11-13赵明哲沈立锋赵培双唐小松宋博旭聂兵兵

水资源与水工程学报 2023年5期

赵明哲, 樊牧, 沈立锋, 赵培双, 马俊, 唐小松, 罗航, 宋博旭, 聂兵兵

(1.华能澜沧江水电股份有限公司糯扎渡水电厂, 云南普洱 665005; 2.华能澜沧江水电股份有限公司, 云南昆明 650214)

1 研究背景

土石坝在实际运行过程中会经常面临库水位频繁变化以及台风、暴雨等极端天气情况,甚至遭遇多种天气、地质事件叠加的复杂工况,影响土石坝渗流的分布规律及坝坡稳定,众多的影响因素使得土石坝渗流过程具有复杂性、随机性等特点,对土石坝安全运行提出了严峻挑战[1-4]。由于外界扰动及测量误差的影响,实际工程中的渗流监测数据并不是渗流量、渗透压力、水位等指标的真实值[5]。因此,为保障土石坝的运行安全,通常构建渗流预测模型,分析实际渗流监测过程的变化规律,建立土石坝渗流监测模型,挖掘渗流序列的随机性、趋势性、周期性特征,实现渗流监测资料的分析、评估与修正[6]。

目前,大量学者基于回归分析原理建立了考虑上下游水位和降水量等要素的土石坝渗流模型,且已取得丰富的研究成果。基于回归分析的土石坝渗流监测分析模型与方法主要包括多元线性回归模型[7]、多元非线性回归模型[2]、时间序列预测模型[8]、机器学习算法[9](支持向量机、相关向量机、神经网络)等。研究表明,人工智能和机器学习技术在处理土石坝渗流预测模型等非线性复杂问题中具有明显优势[10]。Beiranvand等[11]对基于人工智能、机器学习技术的独立模型与混合模型预测土石坝渗流及孔隙水压力的相关研究进行了综述,分析了不同大坝渗流建模方法的使用条件和有效性。Li等[12]选取27个影响土石坝渗流预测模型精度的要素,建立了基于随机森林算法的大坝安全监测模型,并量化了各要素对模型的贡献率。He等[13]基于贝叶斯网络(Bayesian network)构建了土石坝安全智能评价框架,评估了土石坝渗流破坏的极端风险。张鹏等[6]根据土石坝渗流影响要素的滞后效应,探究了上下游水位及降水量共同作用下大坝渗流的变化规律。此外,部分学者还针对土石坝渗流监测的误差问题,采用误差修正模型[14]以及卡尔曼滤波算法[15]等方法,对渗流监测结果进行了处理。Rehamnia等[16]将卡尔曼滤波器与前馈人工神经网络模型相结合,提出了一种大坝逐日渗流量预测模型。

虽然土石坝渗流监测与统计分析研究已取得一定成果,但现有方法主要将渗流监测值的影响要素作为整体进行考虑,构建多要素影响的渗流预测模型。此类方法难以准确刻画各要素对效应量(渗流监测值)的作用特征及贡献量,也不利于精细化描述各要素对渗流监测值的影响过程。此外,现有研究主要以确定性方法为主,难以考虑渗流监测结果的随机性和波动性。

因此,本研究针对土石坝渗流监测分析在预测模型、响应解析等方面的不足,提出基于GAMLSS-GLO及随机森林算法的土石坝渗流监测模型,以糯扎渡水电站心墙堆石坝为实际工程案例开展相关研究。首先,筛选前7 d无降水条件下量水堰监测的大坝渗流量,构成无降水影响的大坝渗流序列,采用随机森林算法,构建无降水条件下渗流量与上下游水位的回归模型;考虑渗流量受前期累积降水的综合影响,提出大坝渗流监测的综合降水因子;在此基础上,引入广义可加模型(generalized additive models for location, scale and shape of generalized logistic distribution, GAMLSS-GLO),模拟降水影响下土石坝渗流监测值的波动特性;将水位影响下渗流回归过程与降水影响下渗流的波动区间相叠加,搭建土石坝渗流监测的区间预测模型。通过上述研究以期提高渗流模拟预测的质量,为土石坝渗流安全监控、合理评价及预警预报提供依据。

2 土石坝渗流分析模型与方法

2.1 基于随机森林算法的水位-渗流量回归模型

近年来,机器学习算法发展迅速,此类方法通过样本训练确定模型的结构和参数,拟合变量间的相依关系,已广泛应用于各个领域,在大坝渗流预测上亦得到了成功应用[11]。本研究采用参数设置简单、易实现、精度较高的随机森林算法(random forest algorithm),建立土石坝渗流量与上下游水位的相关关系模型,对渗流的水位影响分量进行回归及还原计算,进而对渗流监测序列进行分解。

基于随机森林算法构建水位-渗流量的回归模型时,采用Bootstrap方法从总体中抽取样本构成训练集,计算集合特征,再通过分类回归树(classification and regression tree, CART)算法生成回归模型决策树[17],并且以最小均方差作为决策树节点分裂的依据,如公式(1)所示。

(1)

式中:m为决策树节点分裂的最小均方差;s为节点包含的所有训练集;A为节点抽取的特征集;yi为子集的输出值;D1和D2为节点全集s根据特征A分裂的子集;c1和c2为两子集的均值。对于任意节点,根据公式(1)计算使得均方差达到最小的分裂方式及其生长信息。

训练过程中,重复计算各节点的分裂生长信息,当计算达到决策树深度、节点最小样本数、最小均方差阈值等指标的终止条件时,得到Bootstrap抽样训练集的回归决策树。对抽样得到的所有训练集进行训练,便形成随机森林回归模型。

2.2 大坝渗流综合降水因子分析方法

大坝渗流量的监测值是一定时效期内库水位和降水等因素动态变化作用下的瞬时效应量[2],考虑到糯扎渡大坝的规模等特征,结合量水堰实测的渗流量序列与水位、降水序列的定性分析结果,确定其大坝渗流监测值会受到前7 d累积降水的影响,并且其影响作用呈现出复杂的非线性关系。因此,本研究采用综合降水因子反映前期累积降水对渗流监测值的扰动作用。影响渗流监测值的综合降水因子(PrecipFactor)计算公式如下:

PrecipFactor=(Pday1·θday1+Pday2·θday2+…+

Pday7·θday7)θfix

(2)

式中:Pday1,Pday2,…,Pday7分别为渗流监测时间前1 d至前7 d的降水量,mm;θday1,θday2,…,θday7分别为逐日降水影响渗流量的效用系数;θfix为修正系数。

为量化逐日降水量对渗流监测结果的影响,以综合降水因子与渗流监测降水分量的相关系数最大为目标,采用粒子群优化算法(particle swarm optimization, PSO),优化确定逐日降水影响渗流的效用系数,其目标函数如下:

(3)

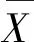
2.3 大坝渗流波动降水影响区间的GAMLSS-GLO模型

降水导致渗流监测值的波动特性与降水的大小具有较强的相关性。从统计学角度来看,如果将土石坝渗流监测值的波动作为随机变量,则其概率分布将随综合降水因子的变化而发生变化,即概率分布各阶矩表现出随综合降水因子演化的特征。

传统的概率统计方法(如固定的概率分布模型)难以反映渗流监测值的波动随综合降水因子的变化情况,而分位数回归方法则难以全面反映不同降水状态下渗流监测值波动的分布特征。为了更为准确地模拟降水条件下土石坝渗流量监测结果的波动特性,本研究参照非一致水文频率分析中应用的时变矩模型(time-varying moments model)和广义可加模型(generalized additive models for location, scale and shape, GAMLSS)对趋势性演化的水文序列进行了分析[18],并提出了渗流降水影响分量的GAMLSS模型。

2.3.1 大坝渗流监测波动量的概率分布考虑到统计分析中常用的正态类(正态分布和对数正态分布)、Г类(指数分布、Gamma分布、P-Ⅲ分布、对数P-Ⅲ分布)、极值类(广义极值分布、Gumbel分布、Weibull分布)等分布类型通常情况下为右偏态(正偏)形式,其左偏态(负偏)形式下参数取值范围与分布函数、密度函数的形式将发生较大变化,不适合用于构建降水影响下土石坝渗流监测波动量的概率分布。

广义逻辑分布(generalized logistic distribution)具有灵活可靠、适应性强等优势[19],可用于描述土石坝渗流监测波动随机变量的分布情况。为了满足渗流监测波动样本序列的不同偏态特性,本研究采用Hosking于1997年提出的考虑偏斜系数的V型GLO分布,构建大坝渗流监测波动随机变量的概率分布。GLO-V分布的累积分布函数、概率密度函数以及累积分布逆函数如下:

(4)

(5)

(6)

(7)

式中:F(x)和f(x)分别为GLO-V分布的累积分布函数和概率密度函数;x(F)为GLO-V分布累积分布的逆函数;μ为位置参数,μ∈(-∞, ∞);α为尺度参数,α∈[0, ∞);k为偏斜参数(系数),k∈(-∞, ∞)。

为了反映GLO-V分布对于左偏态和右偏态样本序列的适应性,给出了当μ=0,α=2,k={-0.45,-0.30,-0.15,0,0.15,0.30,0.45}时,GLO分布的正-负偏态示意图,如图1所示。

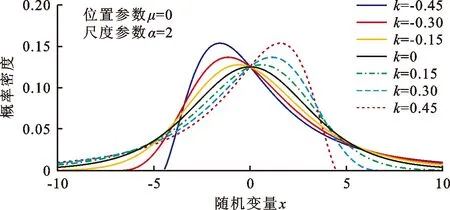
图1 不同偏斜参数下GLO分布正-负偏态示意图

从图1可以看出,GLO-V概率分布对不同样本的适应性较强,特别是对于其概率密度函数的偏态特征,当其偏斜参数k<0时,分布呈左偏态;当偏斜参数k>0时,分布呈右偏态;当偏斜参数k=0时,分布呈现正态化特征。因此,选取GLO-V线型构建大坝渗流波动分布具有合理性。

2.3.2 土石坝渗流监测波动的GAMLSS模型综合降水因子作为与渗流监测值物理相关的随机变量,可扩展渗流监测波动概率分布估计的信息量。非一致水文频率分析的相关研究中,为了在估计水文变量概率分布时考虑相关变量的信息,将随机变量概率分布的一阶矩、二阶矩或分布参数解释为随降水、时间、气温、径流等协变量演化的变量,拟合参数变化情况下随机变量的概率分布[18]。因此,为了充分利用降水信息,尽可能准确地描述大坝渗流监测值的波动特征,以综合降水因子作为大坝渗流监测波动GLO-V概率分布参数的协变量,构建大坝渗流波动区间的GAMLSS-GLO模型。

设渗流降水影响分量的波动变量服从3参数的GLO-V概率分布,则大坝渗流波动区间的GAMLSS-GLO模型为FY,XPrecipFactor(Y│μX,αX,kX),其中μX、αX、kX为渗流波动量序列的分布参数。通过协变量综合降水因子XPrecipFactor和分布参数演化方程系数θevolu,可以将GAMLSS模型的概率分布参数、协变量和演化方程系数之间的关系利用函数关系式(7)～(9)来表示[20]:

μX=gμ(θμ|X=XPrecipFactor)

(8)

αX=gα(θα|X=XPrecipFactor)

(9)

kX=gk(θk|X=XPrecipFactor)

(10)

式中:gμ(·)、gα(·)和gk(·)为GAMLSS-GLO模型分布参数的演化方程,常见的演化方程包含线性函数、多项式、幂指函数、对数函数等;θμ,θα,θk为模型各分布参数演化方程的系数,(θμ,θα,θk)⊆θevolu;μX,αX和kX为协变量预测值XPrecipFactor=X时的分布参数。

2.3.3 GAMLSS模型参数估计与拟合优度检验方法 GAMLSS模型通常采用极大似然法估计参数。由于GAMLSS模型概率分布的样本序列还包含对应的协变量,因此可以通过计算样本序列及其协变量组合的条件对数似然函数值,使全序列条件对数似然函数之和最大的分布参数演化方程系数θevolu成为GAMLSS模型的最优参数[16],其具体计算公式如下:

lCondition(θevolu)=∑ln(fY(Y|XPrecipFactor;θevolu))

(11)

式中:lCondition(θevolu) 表示GAMLSS模型深化方程系数为θevolu时的条件对数似然函数之和;fY(Y│XPrecipFactor;θevolu)表示当渗流波动随机变量和综合降水因子协变量分别为Y和XPrecipFactor时渗流波动量分布的概率密度函数值。

采用模型残差Q-Q图(quantile-quantile plot)、Worm图,以及K-S检验(Kolmogorov-Smimov)方法对GAMLSS模型的拟合优度进行评价。K-S检验统计量的计算公式如下[18]:

(12)

式中:DK-S为K-S检验统计量;t为样本序列中的样本;N为序列中的样本容量;ut=F(yt│θ),为第t个样本的理论频率;ue,t=rank(yt)/(1+N),为第t个样本排频的经验频率。当DK-S小于置信水平α的临界值Dα时,所选理论分布通过K-S检验。

2.4 计及水位与前期累积降水的土石坝渗流监测区间预测模型

将上述提出的基于随机森林算法的水位-渗流量回归模型与大坝渗流波动的降水影响区间GAMLSS-GLO模型相结合,通过渗流水位影响分量与降水影响波动区间的叠加,搭建计及水位与前期累积降水的土石坝渗流监测区间预测模型。其主要步骤如下:

(1)对渗流量、上下游水位、降水量数据样本序列进行预处理,即审查数据的可靠性,插补或剔除缺测值和异常值等,根据日降水数据,将样本总体划分为前7 d有降水影响和前7 d无降水影响的两个子序列;

(2)基于随机森林算法,根据前7 d无降水影响的水位和渗流子序列,构建上下游水位与大坝渗流量的回归模型;

(3)针对前7 d有降水影响的水位、降水和渗流量子序列,根据上下游水位,采用步骤(2)构建的回归模型计算渗流的水位影响分量,将其与实测渗流序列作差,确定渗流的降水影响分量;

(4)根据渗流的降水影响分量及其对应的降水量序列,以综合降水因子与渗流监测降水分量的相关性最强为目标,采用粒子群算法求解前期降水影响效用系数,计算综合降水因子;

(5)根据渗流的降水影响分量和综合降水因子序列,采用GAMLSS-GLO模型建立渗流波动量与降水因子的关系,模拟前期累积综合降水影响下大坝渗流监测值的波动区间;

(6)将步骤(2)和步骤(5)的渗流-水位回归模型与渗流-降水波动区间模拟模型得出的渗流影响分量与降水影响分量叠加,搭建计及水位与前期累积降水的土石坝渗流监测区间预测模型,确定土石坝渗流监测值的可靠区间。

3 实例应用

以糯扎渡水电站心墙堆石坝为例,开展大坝渗流量监测数据的分析预测研究。该坝位于我国云南省普洱市思茅区和澜沧县交界处的澜沧江下游干流,心墙堆石坝最大坝高为261.5 m,在同类坝型中居亚洲第1、世界第3。

糯扎渡大坝渗流监测采用量水堰、渗压计、测压管和水位孔多种方式协同进行。其中,下游围堰处量水堰监测的大坝渗流量为大坝渗流安全监测的首要指标。糯扎渡大坝渗流量采用定时监测(每天1次,早上8:00自动监测并记录)与手动加密监测(根据需要设定加密监测的时间和密度)相结合的方式进行监测。本研究采用2019年1月1日—2022年10月15日糯扎渡大坝下游围堰处量水堰逐日的大坝渗流监测数据,以及水库上下游水位和日降水量进行实例研究,样本序列如图2所示。

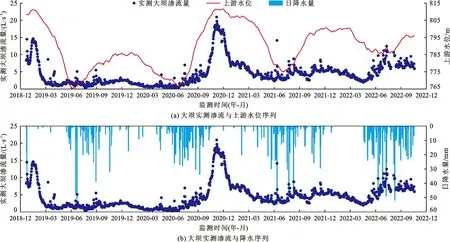
图2 糯扎渡心墙堆石坝渗流实测样本序列

由图2可以看出,大坝渗流量的监测结果与上游水位及降水量具有显著的相关性,符合一般规律。然而,图2所示的渗流监测序列的统计规律在2022年6月前后发生了明显变异(5月底监测的大坝渗流量均值约为4.3 L/s,6月中旬以后监测的大坝渗流量均值超过了7.6 L/s),该时期水库上游水位稳定在780 m附近(属水位影响不敏感段),且刚进入雨季,降水条件类似。经调查电站于2022年5月25日更换过量水堰的流量监测设备,并于当年6月上旬连续对监测设备基准值进行了调整。因此,初步推断变异点前后测值差异为监测设备更新导致的误差。

为了清楚地反映大坝渗流的真实情况,将样本序列分成两段,其中,2019年1月1日—2022年4月30日的数据用于模型的训练和验证;采用所建立的渗流监测模型对2022年5月1日—2022年10月15日的大坝渗流监测值进行分析与评估,并对异常数据进行修正,以提高监测数据的可靠性。

3.1 大坝渗流量-水位关系回归分析

将上游库水位及下游尾水位作为预测变量,将糯扎渡大坝下游围堰处布置的DB-WE-11型量水堰监测的渗流量作为响应变量,选取渗流量监测日期前7 d均无降水的数据组成样本序列,并且按80%和20%的比例从样本序列中随机抽取数据分别作为模型的训练集和验证集,采用随机森林算法,构建无降水条件下糯扎渡大坝渗流量的随机森林回归模型,渗流量模型预测效果及其与水头的相关关系如图3所示。

图3 无降水条件下渗流量模型预测效果及其与水头的相关关系

由图3可知,随机森林算法构建的渗流量回归模型拟合效果较好,且较为稳定。对比训练集与验证集模型的拟合优度指标可以看出,训练集的R2=0.990 8、RMSE=0.379 9;验证集的R2=0.968 6、RMSE=0.639 9,验证集模型的拟合效果仅略低于训练集,表明该模型能够较好地反映无降水条件下大坝渗流量与上下游水位的映射关系。结合图3(b)中大坝渗流量与水头的关系可以看出,不受降水影响的情况下,渗流量与上下游水位的关系非常稳定,与水头大致呈指数关系。当水库的水头从170 m增长到200 m时,大坝渗流量从1 L/s增大到5 L/s,渗流量增量与水头增量的比值为0.13∶1;而当水库的水头从200 m增长到210 m时,大坝渗流量从5 L/s增大到超过19 L/s,渗流量增量与水头增量的比值达到1.4∶1,该两个水头段的大坝渗流量对水头的敏感性相差10余倍,表明糯扎渡大坝渗流量对高水头极为敏感,而水库水头较低时大坝渗流量则相对平稳。

3.2 大坝渗流监测响应分解与降水综合影响

为了较为准确地分析大坝渗流量受水位、降水等因素的影响,考虑将各要素影响下的渗流分量进行分解,进而分析各要素对渗流监测值的影响效应与程度,实现对土石坝渗流安全重要影响因素的监控。利用构建的水位-渗流量随机森林回归模型,模拟对应上下游水位过程在无降水条件下产生的大坝渗流过程,即渗流监测值的水位影响分量;将渗流水位分量从实测大坝渗流量中扣除,得到大坝渗流监测值的降水影响分量。

通过上述方法,分解糯扎渡大坝下游围堰量水堰监测渗流序列的水位影响分量和降水影响分量,并对各分量的渗流响应关系与效用进行分析,结果如图4所示。

图4 大坝下游量水堰监测渗流量的水位、降水响应关系

图4中无降水影响的渗流量为仅受水位影响的大坝渗流量模拟过程,即渗流量-水位随机森林回归模型的模拟结果,其与下游量水堰实测的大坝渗流过程的差值即为渗流降水影响分量,反映了渗流监测值受降水影响的情况。对比分析渗流降水影响分量与综合降水因子的关系可以看出,大部分时段的渗流降水影响分量与降水的变化过程一致,两者图形形状大致呈对应关系。表明渗流量监测值对水位、降水因素响应关系的解析结果具有合理性。

在上述分析的基础上,采用多元线性回归方程确定大坝渗流综合降水因子,研究大坝渗流监测值受前期降水的累积影响。根据分解的渗流降水影响分量和日降水量序列,以降水因子与渗流降水分量的相关性为目标,采用PSO(粒子群)算法优化确定大坝渗流监测值受到降水影响的效用系数θday=[1.000, 0.964, 0.772, 0.794, 0.758, 0.402, 0.202],综合降水因子修正系数θfix=0.519 8。可以看出,近2 d的降水对渗流监测值的影响最为显著;随时间延长,降水对渗流的影响逐渐衰减,监测日期之前第7 d的降水对渗流的影响系数仅为0.202,超过7 d的降水则不再影响大坝渗流量的监测结果。

3.3 基于GAMLSS-GLO模型的渗流-降水波动模拟

为进一步分析前期降水综合影响下渗流监测值的波动特征,构建基于GAMLSS-GLO的渗流量波动-综合降水因子模拟模型。根据上述得到的渗流降水影响分量与综合降水因子序列,采用PSO算法求解最优GAMLSS-GLO模型(拟合优度评价指标lCondition(θevolu)=1019.934),其分布参数演化方程见方程式(13)～(15);采用K-S统计检验、模型残差Q-Q图和Worm图直观反映GAMLSS-GLO模型的拟合效果,如图5所示。

图5 降水影响下大坝下游量水堰监测渗流量波动的GAMLSS-GLO模型拟合效果

μX=6.474×10-5X3-3.794×10-4X2+4.610×10-2X+3.240×10-2

(13)

αX=-3.028×10-7X4+2.744×10-5X3-1.226×10-3X2-3.944×10-2X+3.033×10-2

(14)

kX=-4.780×10-11X6+1.009×10-7X5-1.260×10-5X4+5.667×10-4X3-1.110×10-2X2+0.1061X-0.836

(15)

式中:X为综合降水因子的实际值,根据方程式(13)～(15)可计算该降水条件对大坝渗流监测结果的影响概率。

上述结果表明,GAMLSS-GLO模型位置参数μ、形状参数α和偏斜系数k演化方程的阶数分别为三阶、四阶和六阶。K-S检验统计量DK-S=0.0997(显著性水平α=0.05时K-S检验的临界值Dα=0.1025),通过假设检验,证明GAMLSS-GLO模型是合理的,其模拟结果能够反映渗流监测值波动随综合降水因子的变化规律。由图5可以看出,模型残差正态Q-Q图中残差样本点基本落在1∶1线附近,模型残差Worm图中残差样本点接近于x轴(y=0)直线,且均落在95%置信区间的灰色区域内呈扁平分布,表明模型的拟合效果良好。为体现GAMLSS-GLO模型的优势,将该模型求解的大坝下游量水堰渗流量监测值波动置信区间与分位数回归方法的计算结果进行对照,如图6所示。

图6 降水影响下GAMLSS-GLO模型与分位数回归方法求解的渗流量量水堰测值波动分析

由图6可知,两种方法求解的综合降水因子与量水堰渗流监测值的波动特性规律大致相同,综合降水因子增大也将引起渗流监测值的增大,但不同降水条件下渗流监测值的波动范围无明显变化,总体上表现为渗流监测值相对中位数正偏的波动范围大于负偏,说明渗流监测值的负偏较为集中而正偏相对分散,且相同的偏离程度下负偏的概率更高。不同置信水平下大坝渗流监测值的波动特性方面,随着置信水平的提高,渗流监测值波动区间的宽度大幅增加,当置信水平小于90%时,渗流监测值波动区间宽度约为3 L/s,即相对其中位数的波动范围大致在[-1, 2]以内,且该区间基本不随综合降水因子而变化;当置信水平增加到99%时,渗流监测值波动区间的宽度约为8 L/s,且相对其中位数的波动范围随综合降水因子的变化而变化,具体为正偏先减小后增大,而负偏先增大后减小,其拐点出现在综合降水因子约等于32的点附近。

此外,基于GAMLSS-GLO的渗流量波动模型较分位数回归模型更为全面,能够提供任意降水条件下连续的渗流波动量概率分布,有利于土石坝渗流量监测值的区间预测。因此,本研究推荐采用GAMLSS模型分析大坝渗流监测值的降水综合影响,并分别给出了降水影响下渗流波动的概率密度分布(probability density function, PDF)和累积概率分布(cumulative distribution function, CDF),如图7所示,可为后续渗流区间预测及修正研究提供依据。

3.4 大坝渗流监测值的区间预测

根据糯扎渡大坝渗流回归分析、水位与降水要素分解及各要素与渗流响应关系解析的结果,通过水位-渗流量回归模型计算上下游水位影响的渗流分量,利用大坝渗流波动的降水影响区间GAMLSS-GLO模型计算给定置信水平下渗流降水分量波动的置信区间,将两分量叠加得到计及水位与前期累积降水的土石坝渗流监测可靠区间,如图8所示。

图8 糯扎渡大坝渗流监测值区间预测结果

由图8可以看出,在2022年5月以前(建模数据序列),糯扎渡大坝下游围堰侧量水堰监测的渗流样本点连续,规律性较强,实测点几乎全部落在95%的置信区间范围内,且大部分样本点紧靠预测区间的中位数,交叉验证了大坝渗流监测值区间预测模型和量水堰渗流监测数据的合理性与可靠性。对于2022年5月至10月(实验数据序列),5月份大坝渗流监测值和区间预测结果与建模序列基本一致,但在更换过量水堰的流量监测设备(5月25日)并对新监测设备基准值进行调整(6月中上旬)之后,为保证模型对变异序列的适应性,根据变异前后样本的均值,将水位-渗流回归模型增加了跳跃变异增加的均值。结果表明,处理后模型对于全部实验序列的模拟效果均良好,变异前后监测值基本都落在置信区间内。此外,该模型还具有评估渗流监测序列的功能,当监测值偏离置信区间时,可向大坝安全监测人员提供预警信息,并对缺测或异常的数据样本进行插补或修正。

4 讨论

本文针对影响土石坝渗流观测结果的两类关键要素,即水位和降水,基于分解合成的思想,采用随机森林算法构建无降水条件下渗流量与上下游水位的回归模型,同时引入GAMLSS-GLO模型量化降水对渗流监测的影响。

在无降水条件下,渗流量回归模型训练期精度达到99.08%,验证期精度达到96.86%,上下游水位与渗流量的关系较为稳定且不受降水的影响,这一模拟结果优于已有的大部分同类模型[21]。例如,Li等[12]基于随机森林算法构建的大坝安全监测模型的平均预测精度为95%;吕鹏[1]采用自适应差分演化(differential evolution adaptive metropolis, DREAM)算法将渗透系数反演值代入数值模型后得到97%的模拟精度。

在降水对渗流监测的影响方面,通过综合降水因子反映了降水对渗流监测的滞后性影响,其结果与其他研究的结论一致[5]。采用GAMLSS-GLO模型计算了降水影响下的渗流量监测的偏差特性,研究结果与吴雄伟等[14]、冯春燕等[15]关于土石坝渗流监测偏差修正的研究结论一致。总体来看,本研究提出的基于GAMLSS-GLO及随机森林算法的土石坝渗流监测模型可提高渗流模拟精度,降低不确定性的影响。