基于CBR试验的隧道弃渣级配碎石细观力学参数研究

岳夏冰, 黄 姣, 丁 同, 王奕丁, 王学营

(1.长安大学 公路学院, 陕西 西安 710064; 2.内蒙古自治区交通运输科学发展研究院, 内蒙古 呼和浩特 010051;3.生态安全屏障区交通网设施管控及循环修复技术交通运输行业重点实验室, 内蒙古 呼和浩特 010051)

1 研究背景

随着我国基础设施建设的快速发展,公路、铁路建设中的隧道工程将会产生大量的弃渣,而传统的粗放式弃渣处理方式不利于节约资源保护环境。如若对弃渣进行合理利用,不仅能解决道路建设的原材料问题,而且环境问题也可得到改善[1-2]。目前提倡将隧道弃渣破碎成有一定颗粒级配的碎石,用作路面基层填料。

级配碎石是一种理想的填筑材料,主要由粗、细碎石集料和石屑构成,具有三相性和离散性的特点。其力学模型研究一直是诸多学者关注的热点,学者们对经典模型进行不断完善和改进[3-4],提出了一些新的本构模型[5-6]。近年来,许多研究表明级配碎石的颗粒性结构特征和非线性力学特性与层状弹性体系理论假定的均质的、连续的、均匀的、各向同性结构存在差异[7-9]。故有限元法在模拟级配碎石内部作用机理时具有一定局限性,而离散元法可以模拟离散介质,能更好地模拟级配碎石的内部作用。朱俊高等[10]、李灿等[11]、吴跃东等[12]利用颗粒流软件(particle flow code, PFC)分别对不同级配和密实度土石的三轴试验、室内三轴固结排水试验、击实试验及加州承载比 (California bearing ratio, CBR)试验模型进行了模拟,得出诸多结果。张振平等[13]利用颗粒离散元理论和PFC2D建立了土石混合体离散元模型,对不同含石量、不同黏结强度混合体进行了直剪试验模拟。朱遥等[14]通过直剪试验和离散元模拟探究了颗粒形态对砂土抗剪强度的影响,发现不规则颗粒形态的石英砂的抗剪强度更大。任皎龙[15]、丁同[16]利用PFC进行级配碎石CBR试验的离散元模拟得出了级配碎石细观力学参数的一些性质。徐文杰等[17]基于真实块石形态构建了土石混合体的数学模型,并结合相关算法开展了三维数值的直剪试验研究。总体而言,目前学者们多用直剪、三轴试验等室内试验与离散元软件相结合的方法对级配碎石进行研究[18-23]。对于隧道弃渣制成级配碎石,离散元法建模过程中的细观参数标定十分重要,但目前对于其力学性能与细观参数关联性的研究较少,其细观力学参数对级配碎石路面性能指标的影响尚不够明确。

路面基层的承载能力对路面结构性能起决定作用,由隧道弃渣制成的级配碎石做基层填料,其承载力与耐久性等对公路安全十分重要。本文依托于隧道洞渣加工再利用项目,借助颗粒流软件PFC3D对CBR试验试样展开研究,探讨级配碎石颗粒细观力学参数对其路用性能指标的影响。

2 CBR试验模型初始设定及构建

2.1 CBR试验及模型选择

本文基于外加工隧道洞渣,借助PFC3D研究其路面基层填筑用级配碎石的细观力学性能。将现场取样的碎石土进行筛分并参考相关研究[24]进行级配优化(见表1)后进行试验,为后续模拟试验提供数据支持及参照。

表1 碎石土室内试验级配

在离散元模型建立过程中考虑到实际工程中碎石个体形状的复杂性,可改变颗粒接触模型及调整相关参数来模拟颗粒形状对结果的影响,利用转动阻力线性模型对颗粒接触中的法向力、切向力、摩擦力以及咬合力的影响进行模拟,并将其与线性接触键模型进行对比分析。

2.2 CBR模型设计

2.2.1 细观参数标定 根据相关研究[25],对于线性接触模型与转动阻力模型需确定碎石土颗粒的细观参数,通过反复模拟试算得到与CBR试验结果较吻合的模拟结果,如表2所示。

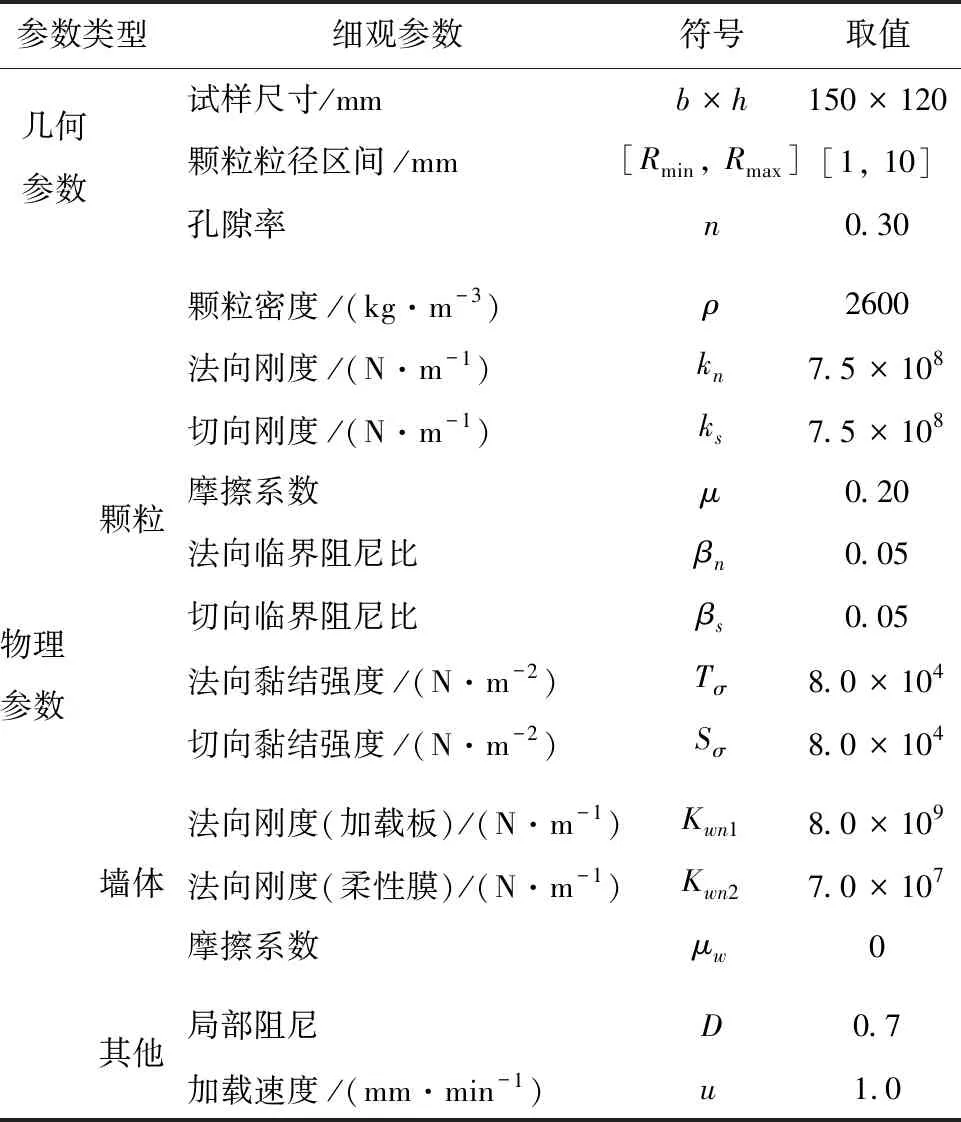
表2 碎石土颗粒细观参数

2.2.2 CBR模型构建 按照表2中颗粒细观参数设置CBR模型参数,根据CBR数值试验中试样的边界条件构建模型。在设定范围内生成颗粒,由于重力影响,自上而下力链网络趋于密集。自顶面墙体往下施压,以试件被力链整体竖向贯穿作为固结完成的标志。

删除顶面墙体,设立1、2、3号墙体共同组成模拟压头,模拟压头即模拟CBR数值试验中的贯入杆。在模拟压头左、右两侧的试样顶面均设置一宽度为50 mm的荷载板,用以阻止试样颗粒被挤出,同时维持其边界条件,如图1所示。开始前设定其初始荷载为45 N,考虑实际试验中试样所受压力,在4、5号墙体处施加25 N的力,利用伺服机制确保整个过程中4、5号墙体应力不变。当试样边界的加载情况符合试验要求后,令贯入杆以恒定速度1.25 mm/min压入试样,贯入量达到6 mm时停止。

图1 CBR数值试验边界条件示意图

图2为室内试验与数值试验的CBR曲线对比;表3为室内试验与数值试验所得CBR值的对比。由图2可见,两曲线的总体发展趋势较为一致,且CBR试验的初期单位压力增长较快,也符合实际试验情况,由此说明数值模拟试验有效。

图2 室内CBR试验与数值CBR试验曲线对比

表3 室内试验与数值试验所得CBR值对比

由表3可知,室内试验与数值试验CBR值的偏差为5.33%,说明数值试验的试验结果与真实情况相差较小,同样验证了CBR数值实验结果的有效性。故可在此基础上开展级配碎石颗粒细观力学参数研究。

3 CBR试验细观力学机理分析

对CBR试样颗粒而言,贯入过程即为嵌挤和摩擦的过程,利用颗粒流软件PFC3D可实现颗粒状态观测,从细观角度解释其力学机理。

3.1 接触力链分布

试验中试样表面所受单位压力随着贯入量的增大而相应增大,并能在试样颗粒间逐渐形成力链传递应力。初期接触力链发展较为均匀,试样发生压实及弹性变形。根据贯入杆与颗粒距离的不同,离其较近墙体处的颗粒会先被压实,在贯入力作用下水平向力链得到发展。试样力链随着贯入量而发展,当其竖向贯穿时即标志着试样进入剪切阶段。

图3为贯入量分别为1.25、2.5、5.0和6.0 mm时主要节点接触力链的演变过程。由图3可知,整个试验中,随贯入量的增加,力链向下增长至试样底部;中层的水平向力链延伸至边界;试样四角几乎无力链。表明力链网络主要以橄榄球状呈竖向发展,而水平向发展较少。

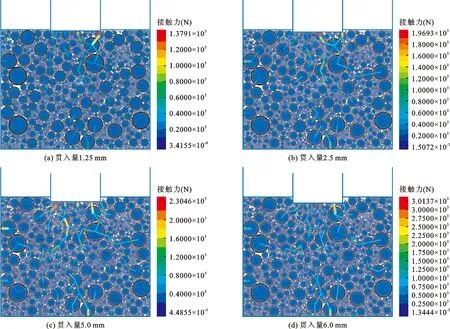
图3 CBR数值试验接触力链随贯入量的演变过程

图4为相应试样颗粒的接触力最大、最小值与接触数随贯入量的变化。由图4可见,试样颗粒的接触力最值与贯入量呈正相关,即所有接触力均随贯入量的增加而增大;贯入量继续增加,接触力最大值增大而最小值变化不大。主要是当力链延伸至试件底部时,在上部荷载板周围颗粒间会出现最小值。接触数可表征贯入过程中颗粒间的挤密程度及力链增长情况,其值越大,表明颗粒密度越大,则其对应的力链网络越密集。

图4 试样颗粒的接触力最值及接触数随贯入量的变化曲线

3.2 位移矢量场分布

由于试样颗粒发生位移产生的位移矢量绝对值过小,不便观察,故采用放大系数SA对其模拟结果进行放大显示。图5为SA分别取为6.87,3.45,1.55,1.35下各贯入量对应颗粒位移矢量场分布。通过对图5中试样颗粒在不同贯入量下对应的位移矢量场分布情况进行分析对比得出,当贯入量较小时,位移矢量方向主要为竖向;随着贯入量的增加,位移矢量主要呈“人”字形,且与贯入量增加有关;对试样底部而言,中间位置颗粒稳定性最好、位移量最小。

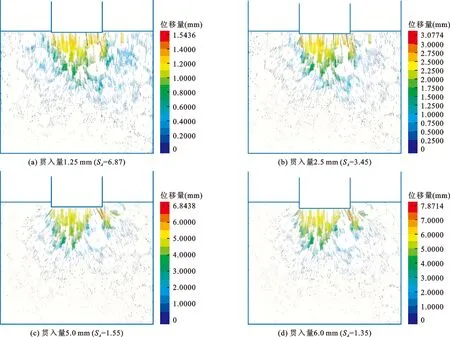
图5 CBR数值试验各贯入量对应的颗粒位移矢量场分布

4 细观力学参数与CBR值关联性分析

实际CBR试验试样颗粒受力情况较复杂,故主要研究颗粒刚度比、摩擦系数、黏结强度、黏结强度比等细观参数与CBR值的关联性。规定接触力最值及接触数统一选取贯入量为6 mm时的数值,以确保数据的合理与完整,同时由于颗粒接触力最小值通常发生在力链末端,与力链网络关系不大,故分析时接触力最小值仅作参考。

4.1 颗粒刚度比kn/ks

因固结后接触力为零,设定同一颗粒的接触键法向重叠量初始值不随颗粒刚度比的变化而变化。令ks=7.5×108N/m,通过调整法向刚度kn改变颗粒刚度比kn/ks的大小,最终得出kn/ks与CBR值关系曲线及不同kn/ks对应的CBR曲线如图6所示。由图6可以看出,整体上kn/ks对CBR值影响较小,CBR值在一固定值上下波动,不同kn/ks对应的CBR曲线整体变化趋势较为一致。对比kn/ks=0.25及kn/ks=9.0的CBR曲线可见,两者斜率相近。大致以贯入量3.5 mm为界,kn/ks=0.25的CBR曲线前段颗粒所受压力较大,其原因为较小kn下颗粒间的法向可重叠量较大,可产生的弹性变形多对应所承受的法向力。而贯入量大于3.5 mm时,kn/ks=0.25及kn/ks=9.0的CBR曲线纠缠重叠,此时切向位移是颗粒间相对运动的主要形式,贯入力受kn的影响削弱。

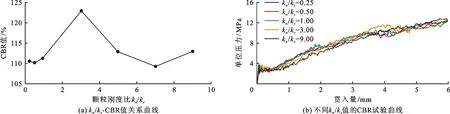
图6 试样颗粒不同刚度比kn/ks下的CBR值与CBR试验曲线

观察图6(b)可知,在贯入量3.5～4.5 mm范围内,CBR曲线均出现类似于应力软化的“台阶”,贯入力未延续增大。这说明试样在此范围内整体产生了较大位移,故在此期间,颗粒接触键以切向破坏为主。对比其后曲线整体发展趋势,表明此后贯入力继续提升,抵抗变形能力增强,由此推断此时试样颗粒进行了位置重分布和力链重构建。

图7展示了试样颗粒不同刚度比kn/ks下相应的力链变化情况。如图7(a)所示,以kn/ks=3为界,颗粒接触力的最大值先增大后减小,整体变化幅度不大。同一应力水平下,kn/ks<3时颗粒接触力最大值增长较快,说明法向可重叠量与弹性呈线性正相关。在距贯入杆底部较远的两角处应力较小,主要是kn较小时,颗粒法向弹性将接触力场范围及梯度增速削弱,上部颗粒的重力作用为颗粒受力的主力。随着kn的增大,颗粒接触力场逐渐向外扩展,由此产生的颗粒接触力占全部底部接触力的比例提高。当kn/ks>3时接触力最小值增加速率减缓甚至呈现下降趋势,其原因主要是在kn较大的情况下,接触键的法向力不易增大,而切向力持续增大,切向破坏的发生使得颗粒接触力最小值的增幅不大。由图7(b)可见,kn/ks与颗粒接触数近似呈线性正相关,即kn/ks与应力场范围、各梯度增速基本呈线性相关。同样当kn/ks<3时,应力场范围扩大、梯度值增大,两者共同作用的影响使得曲线的斜率较大;当kn/ks>3时,曲线的斜率变小是因为此时应力场扩散至全部试样范围,故斜率大小仅受应力场梯度值的影响。

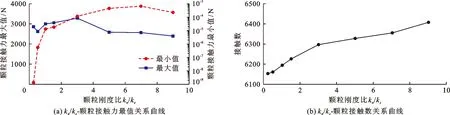
图7 试样颗粒不同刚度比kn/ks下的力链变化情况

4.2 颗粒摩擦系数μ

图8为颗粒摩擦系数μ与CBR值关系曲线及不同μ值对应的CBR曲线。由图8可见,颗粒摩擦系数对试样的宏观力学性质影响较大;CBR值随摩擦系数的增大基本呈线性增长(图8(a)),各摩擦系数对应的CBR曲线具有明显的离散性(图8(b))。当贯入量处于0～1 mm范围内时,各μ值情况下压力增长路径大致重合,此阶段压实及弹性变形为试样颗粒变形的主要组成部分,大部分颗粒尚未产生动摩擦。当贯入量大于1 mm后,不同μ值对应的各CBR曲线斜率增长存在显著差异,各曲线整体均呈正线性增长。由此推断颗粒摩擦系数μ主要作用于颗粒的动摩擦阶段,且位移场的范围与μ的影响范围高度一致。

图8 试样颗粒不同摩擦系数μ下的CBR值与CBR试验曲线

图9展示了不同μ下相应的力链变化情况。由图9(a)可见,μ与接触力最大值之间近似线性相关,与μ-CBR值关系基本一致。当μ<1.0时,接触力最小值随μ的增大逐渐减小,即随μ的增大会使得力链影响范围变小。具体而言:随着μ的增大,相对位移量因颗粒运动耗能增多导致其动能减少而相应减小。另外,颗粒位移场范围和梯度值与最小值之间具有高度关联性,当μ>1.0时,颗粒位移场范围和梯度值随接触力最小值的增加而增大。但球形颗粒间的接触面积不大,故颗粒动摩擦所消耗的能量较小,在一定范围外颗粒位移场发展受μ的影响程度降低。图9(b)显示,随着μ的增大,接触数及其变化速率呈现先下降后上升的趋势,这与上述μ与颗粒位移场范围和梯度值关系的变化规律一致。

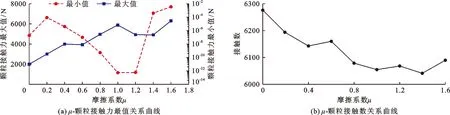
图9 试样颗粒不同摩擦系数μ下的力链变化情况

4.3 颗粒法向黏结强度Tσ

试样整体黏性可用法向黏结强度Tσ模拟,令黏结强度比Tσ/Sσ=1,以法向黏结强度Tσ作为自变量研究其对CBR试验结果的影响,结果如图10所示。由图10(a)可见,Tσ与CBR值呈线性正相关,分析其原因主要是随着Tσ的增大,小粒径颗粒黏附形成的黏结基团整体参与到了力链网络之中,在这一过程中,贯入力一方面要对基团个体做功,另一方面基团内部的变形及破裂也将消耗部分动能,Tσ对CBR值有较大影响。由图10(b)可以看出,随着贯入压力的增大,不同Tσ对应的CBR曲线均呈线性增长,即试验全过程受恒定黏结作用的影响。

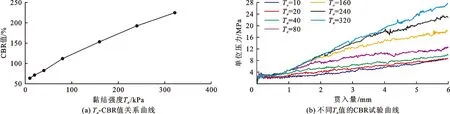
图10 试样颗粒不同法向黏结强度Tσ下的CBR值与CBR试验曲线

图11为不同法向黏结强度Tσ下试样力链变化情况。分析图11(a)可知,Tσ与颗粒接触力最大值正相关,接触力最大值主要发生在与贯入杆底部接触的颗粒上,其原因主要是一方面此位置直接受贯入力作用的影响,另一方面此处Tσ增大所导致的接触力衰减及方向扩散不明显。接触力最小值与Tσ之间呈对数曲线状正相关。在Tσ为400 kPa时接触力最小值出现突变,推测是因Tσ较大时颗粒黏结基团数量和大小均增加所致,此时大粒径颗粒形成的骨架中间出现的大孔隙由小颗粒黏附引起。图11(b)表明,黏结强度Tσ与接触数呈对数性正相关。当Tσ值较低时,试样颗粒类似无黏性土呈散体状态,试样被压缩至完全密实。随着Tσ的增大试样开始出现黏性,即试样从无黏性土过渡到黏性土,原来松散颗粒和周边颗粒间形成接触键。故只要颗粒与黏结基团相互接触,就会被黏附至该基团。但在同一贯入力下由于接触始终有限,颗粒接触数随着Tσ的提高难以继续增大。

图11 试样颗粒不同法向黏结强度Tσ下的力链变化情况

4.4 颗粒黏结强度比Tσ/Sσ

考虑到细观力学行为上切向黏结强度Sσ与法向黏结强度Tσ的差异,为更充分地探讨黏结强度对CBR试验结果的影响,将黏结强度比Tσ/Sσ分为Sσ不变与Tσ不变两组进行CBR模拟试验。

固定切向黏结强度Sσ不变,仅改变法向黏结强度Tσ,不同Tσ/Sσ的CBR试验结果如图12所示。图12(a)中Tσ/Sσ与CBR值的关系可拟合为一对数曲线,当Tσ/Sσ<2时,CBR值随Tσ的增大而增大的速率较快;当Tσ/Sσ>2时,CBR值的增速逐渐放缓。由图12(b)中不同Tσ/Sσ值对应的CBR曲线可见,各曲线在贯入量较小的试验初期有一重叠段,表明试样颗粒在此阶段发生压实挤密,产生了颗粒法向压实以及接触键切向静摩擦。当贯入量达到4 mm时,受切向指标如ks、Sσ等的影响各曲线均呈现为“台阶”状。

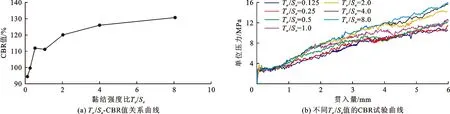
图12 试样颗粒不同黏结强度比Tσ/Sσ的CBR试验结果(Sσ不变)

同样固定切向黏结强度Sσ不变,仅改变法向黏结强度Tσ,讨论不同Tσ/Sσ下试样力链变化情况,如图13所示。由图13(a)中Tσ/Sσ-颗粒接触力最值关系曲线可以看出,当Tσ/Sσ<4时,接触力最大值与Tσ呈正相关,法向拉裂和切向剪断为颗粒接触键的主要破坏形式,Tσ持续增大使得法向拉裂不断减少,即两者呈负相关;当Tσ/Sσ>4后,可能发生法向拉裂的概率降至最低,因而法向拉裂无法随Tσ的增大而继续减小,此时颗粒接触键主要是切向剪断破坏。由图13(b)中Tσ/Sσ-颗粒接触数关系曲线可以看出,接触数随Tσ的变化与Tσ/Sσ呈对数性正相关,当Tσ/Sσ<2时,随Tσ的增大接触数的增长速度较快,故在此范围内,Tσ的增大在接触力场范围及强度增长上具有积极作用,Tσ接近零时,由于颗粒松散相互接触少,接触数也相应减少;当Tσ/Sσ>2时,随Tσ的增大接触数增速放缓,主要是受颗粒表面黏附性增强导致颗粒形成黏结基团的影响。结合图13(a)中颗粒接触力最小值与Tσ之间无明显相关性,认为颗粒接触力场对Tσ的调节作用不敏感。

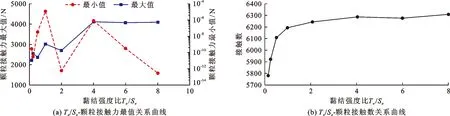
图13 试样颗粒不同黏结强度比Tσ/Sσ下的力链变化情况(Sσ不变)

固定法向黏结强度Tσ不变,仅改变切向黏结强度Sσ,不同Tσ/Sσ的CBR试验结果如图14所示。由图14(a)可知,随Sσ的增大CBR值及其变化速率均在增大。将图14(b)与图12(b)对比可以看出,调整Sσ所得CBR曲线具有更显著的离散性。通过对比Tσ与Sσ两指标对CBR值的影响,可以推断切向指标在试样力学反馈中占主导地位,另根据两者对CBR值影响幅度的差异,判定Tσ、Sσ在颗粒接触键破坏中起的阻碍作用之比大致为1∶3。

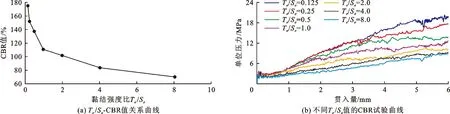
图14 试样颗粒不同黏结强度比Tσ/Sσ的CBR试验结果(Tσ不变)

同样固定法向黏结强度Tσ不变,仅改变切向黏结强度Sσ,讨论不同Tσ/Sσ下试样力链变化情况,如图15所示。由图15(a)可见,取Sσ为自变量时,其颗粒接触力最值的变化趋势与CBR值的变化趋势类似,表明Sσ对颗粒接触力场的性质影响很大。当Tσ/Sσ<2时,Sσ减小接触力最值也随之减小,表明Sσ较大使得颗粒可承受的法向力较大,对接触键的稳定有利;当Tσ/Sσ>2时,接触力最值随Sσ的减小变化平缓,表明散体状态颗粒接触键易出现切向破坏,其原因是此时颗粒间的黏性有法向黏结而缺乏切向黏结。由图15(b)中Tσ/Sσ-颗粒接触数关系曲线可以看出,当Tσ/Sσ<1时,颗粒接触数变化不明显,即在此范围内,无法通过调节Sσ显著改变接触力场。Sσ较大时,切向破坏不易发生,而法向拉裂又必须在有合适空隙时才可能发生,其比切向破坏的发生概率低;当Tσ/Sσ>1时,Tσ/Sσ与接触数为负相关性,随着Sσ的降低,试样颗粒散体化程度提高,表明试样的黏附性与塑性可由法向与切向黏结强度表征,具体为黏附性主要受Tσ影响,接触键切向塑性由Sσ体现。

图15 试样颗粒不同黏结强度比Tσ/Sσ下的力链变化情况(Tσ不变)

5 讨 论

本文借助PFC3D对隧道弃渣制级配碎石进行CBR试验模拟,贯入过程中试样力链网络的发展与位移场的形成及扩大同步,且随着贯入量的增加,单位压力增加速率由快转慢,这与蒋应军等[26]模拟CBR试验过程中得出的贯入量与贯入力的关系曲线具有较好一致性。本研究表明,接触力链自试样底部开始发展且初期需经历一压实阶段,随着贯入杆的深入,试样整体性不断加强,底部逐渐形成圆锥状压实体,压实体不仅能分散竖向接触力,还能作用于接触力场的侧向发展,这与任皎龙[15]对安康瀛湖石灰岩碎石CBR数值模拟得出的发展规律基本一致。在细观力学参数与CBR值关联性分析方面,得出了颗粒摩擦系数μ与CBR值呈线性正相关,与彭安平等[22]研究得出的颗粒间摩擦系数的增加能够明显提高其抗压能力的结论一致。对于颗粒刚度比kn/ks对CBR值及CBR曲线影响的研究方面,本文研究结果表明,不同刚度比kn/ks对CBR值及CBR曲线均影响不大,彭安平等[22]研究认为刚度比对CBR曲线无明显影响,但对CBR值会略有影响,分析这一差异可能是所用级配碎石种类不同所致。关于级配碎石法向黏结强度Tσ、切向黏结强度Sσ以及黏结强度比Tσ/Sσ对CBR试验结果的影响方面,目前还缺乏相关研究,本文通过模拟认为,颗粒黏结强度Tσ与CBR值呈线性正相关,且依据黏结强度比Tσ/Sσ得出切向黏结强度Sσ对CBR值的影响较大。

受计算机计算效率所限,本研究设定CBR试验模拟时的最小颗粒粒径为2.0 mm,忽略了更小粒径颗粒对试验的影响,且未考虑颗粒破碎对整体颗粒级配的影响。在今后的研究中可通过改进离散元算法实现更小粒径颗粒的设定,并利用刚性簇及柔性簇对其进行模拟研究,使CBR试验的模拟结果更为精准,能够更好地反映级配碎石颗粒细观力学参数对CBR试验的影响。

6 结 论

本文用离散元方法对CBR试验进行模拟,研究CBR试验全过程中级配碎石颗粒的运动轨迹并讨论其受力情况,与力链模型结合分析其接触力的传递,由此确定线性接触键模型中kn/ks、μ、Tσ、Sσ等颗粒细观参数对CBR试验结果的作用机理。得出的主要结论如下:

(1)对CBR试验中接触力链与位移场的形成过程分析可以得出:接触力链形成自贯入杆处的颗粒间并不断发展,其力链网络以橄榄球状竖向发展;随贯入的深入,试样底部会出现圆锥状压实体,且其整体性会因颗粒密度增大、边界条件受限而持续提高。

(2)通过改变颗粒刚度比kn/ks、摩擦系数μ以及黏结强度Tσ(设定Tσ/Sσ=1)观察其对CBR试验影响发现:不同颗粒刚度比kn/ks对应的CBR曲线及CBR值均变化不大,无显著影响;摩擦系数μ与CBR值呈线性正相关,且随μ的增大,接触力场范围先减后增;颗粒黏结强度Tσ与CBR值呈线性正相关,即试样从无黏性到黏性过程中接触力场范围及梯度大小相应增大。

(3)不同黏结强度比Tσ/Sσ的CBR试验分为切向黏结强度Sσ不变与法向黏结强度Tσ不变两组,借助黏结强度比Tσ/Sσ,对比切向与法向黏结强度对CBR试验结果的影响得出:切向黏结强度Sσ对CBR值影响较大,切向黏结强度Sσ主确定接触键切向塑性,法向黏结强度Tσ主控制其表面法向黏附性。