高外水隧洞变形稳定性的基质压缩效应

2023-11-13陈科锦李芸娇

水资源与水工程学报 2023年5期

刘杰, 陈科锦, 孙猛, 李芸娇, 姜磊, 徐磊

(1.重庆市水利电力建筑勘测设计研究院有限公司, 重庆 400020; 2.河海大学水利水电学院, 江苏南京 210024; 3.江苏省灌溉总渠管理处, 江苏淮安 223200)

1 研究背景

深埋水工隧洞通常面临高地下水问题[1],如锦屏二级水电站引水隧洞实测外水压力达10.2 MPa[2]、滇中引水工程香炉山隧洞外水压力达13.4 MPa[3],均属于典型的外压控制型隧洞。高外水隧洞承受的外水内渗力学作用具有与开挖释放荷载同向的变形效应,不利于围岩稳定,且明显不同于内水外渗的内压控制性隧洞[4]。为准确分析高外水隧洞围岩的变形稳定性,需在分析中合理模拟外水内渗的力学作用[5]。

现阶段,对水工隧洞外水内渗力学作用的模拟,主要有面力、体力和渗流-应力耦合分析等方法。面力方法[6-7]将外水作用视为施加于衬砌外表面的面力,可以较好地反映外水内渗对衬砌的力学作用,但无法合理体现外水内渗对围岩的力学作用。体力方法[8-10]是将外水内渗的力学作用视为作用于围岩和衬砌的体积力,与面力方法相比,可更为合理地模拟高外水隧洞围岩-衬砌结构体系的实际受力特征,但仍无法体现出围岩-衬砌结构体系受力变形引起的渗流场变化。渗流-应力耦合分析方法不仅可合理模拟渗流场的力学作用,亦可合理体现应力变形状态对渗流场的作用。董鹏等[11]基于多孔介质有效应力原理,开展了高地下水位隧洞渗流-应力耦合分析;Wu等[12]采用直接耦合方法,分析了饱和岩体体积应变对深埋高外水隧洞渗流场的影响;王克忠等[13]采用间接耦合方法,分析了深埋引水隧洞开挖过程中围岩孔隙水压力分布及围岩的变形规律;徐磊等[14]建立了高外水隧洞渗流-应力-损伤-劣化耦合分析模型,分析了灌浆圈劣化条件下高外水隧洞长期服役性态的演化过程。考虑到饱和岩体内的渗流与其应力变形状态之间存在复杂的相互作用,在渗流-应力耦合框架内分析高外水隧洞的变形稳定性是必要的。

另一方面,有效应力原理是岩土类介质渗流-应力耦合分析的理论基石,但如何定义有效应力却仍存争议[15]。李广信[16]指出Terzaghi定义的有效应力适用于各种土,但不适用于岩石与混凝土等非散粒体材料。张国新[17]对比了不同渗流荷载计算方法对饱和岩体应力变形的影响,结果表明施加渗透体积力和浮托力(对应于在渗流-应力耦合分析中采用Terzaghi有效应力)会导致应力变形计算结果明显不合理,原因在于该方法忽略了水对岩石基质的压缩作用。为准确分析高外水隧洞围岩的变形稳定性,需在渗流-应力耦合分析中考虑岩石基质的可压缩性。任青文等[18]通过在有效应力公式中利用Biot系数修正孔压项来体现多孔介质骨架基质压缩对渗流力学作用的影响;杜修力等[19]总结了用于修正Terzaghi有效应力的不同公式。现阶段,虽然学者们已逐步认识到在饱和岩体渗流-应力耦合分析中考虑岩石基质压缩的必要性[20],但仍有不少研究工作是基于Terzaghi有效应力开展的[9,21-22],而对于岩石基质压缩对高外水隧洞变形稳定性的影响,尚未见报道。

为揭示岩石基质压缩对高外水隧洞变形稳定性的影响,本文基于饱和多孔介质有效应力原理和Skempton[23]提出的孔压修正系数,并考虑隧洞围岩渗透特性在围岩受力变形过程中的动态演化,建立高外水隧洞渗流-应力耦合模型并对其进行数值实现;依托某深埋引水隧洞工程,开展不同岩石基质可压缩性条件下高外水隧洞渗流-应力耦合分析,探究高外水隧洞围岩应力变形状态随岩石基质可压缩性的变化规律。

2 考虑基质压缩的渗流-应力耦合模型

2.1 饱和岩体有效应力原理

高外水隧洞围岩可视为饱和多孔介质,故开展基于有效应力原理的渗流-应力耦合分析即可直接体现外水内渗的力学作用。

若忽略固体骨架基质的可压缩性,饱和多孔介质的有效应力即为Terzaghi有效应力[19]:

(1)

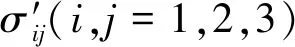
对于土、砂等散粒体材料,其骨架基质(颗粒)压缩系数远大于材料宏观压缩系数[17],忽略骨架基质的可压缩性引起的有效应力计算误差很小,故可采用如式(1)所示的有效应力定义。但对于岩石材料,由于其骨架基质压缩系数与材料宏观压缩系数处于同一量级[17],需在有效应力定义中考虑岩石基质的可压缩性,以合理体现孔隙水压力对饱和岩体有效应力的影响。

Skempton[23]考虑固体基质压缩,推导出体现孔隙水压力对有效应力贡献的修正系数的表达式:

α=1-Cs/Cg

(2)

式中:α为孔压修正系数;Cs为固体材料基质压缩系数,Pa-1;Cg为固体材料宏观压缩系数,Pa-1。李广信[16]给出的各种土、岩石和混凝土的压缩系数比Cs/Cg见表1。

表1 各种土、岩石和混凝土的压缩系数比[16]

应用公式(2)对公式(1)进行修正,可得出考虑固体基质可压缩性的有效应力定义表达式如下:

(3)

在获取岩石宏观压缩系数及其基质压缩系数的基础上,即可通过应用公式(3)在高外水隧洞渗流-应力耦合分析中体现岩石基质压缩的影响。

2.2 饱和岩体渗透性演化模型

为合理模拟外水内渗,需在高外水隧洞渗流-应力耦合分析中考虑围岩应变变形状态对其渗流特性的影响。考虑到受开挖释放荷载等作用影响时,围岩产生的体积应变会改变其孔隙率,并导致其渗透性发生变化,故为了体现高外水隧洞围岩渗透性在其受力变形过程中的动态演化特征,给出孔隙率φ与体积应变之间的函数关系如下[12]:

(4)

式中:φ0为初始孔隙率;εν为体积应变,εν=ε11+ε22+ε33,εii(i=1,2,3)为正应变。

考虑岩体扩容的影响,当εν<0时,应按下式计算孔隙率φ[24]:

(5)

进而,结合渗流力学Kozeny-Carman方程,即可建立体积应变εv与渗透系数k之间的函数关系:

(6)

式中:k0为饱和岩体渗透系数初值,m/s;当εv≥0,取加号,当εv<0,取减号。

φ0的取值受到岩性、岩石结构及赋存环境等诸多因素的影响,变化范围较大。图1给出了φ0=0.003、0.005和0.007时的k/k0-εν关系曲线。由图1可以看出,随着体积应变的增大,饱和岩体渗透系数逐渐增大,且呈现出非线性演化特征;初始孔隙率越小,则体积应变变化对饱和岩体渗透系数的影响越大。

图1 岩石渗透系数比k/k0与体积应变εv的关系曲线

2.3 数值实现方法

为研究岩石基质压缩对高外水隧洞变形稳定性的影响,利用ABAQUS中的SOILS模块开展高外水隧洞渗流-应力耦合分析。

为合理反映外水内渗的力学作用,实现基于公式(3)的渗流-应力耦合分析,在ABAQUS中定义围岩材料属性时,除需给定其宏观弹性模量,还需通过关键字*POROUS BULK MODULI定义其基质体积模量,即基质压缩系数的倒数,以下分析中按下式确定α的取值[17]:

(7)

式中:μ为围岩材料宏观泊松比;Eg为围岩材料宏观弹性模量,GPa;Ks为围岩材料基质体积模量,Pa。

进一步地,为实现基于公式(6)的渗流-应力耦合分析,利用ABAQUS提供的二次开发接口USDFLD,通过编制用户子程序定义场变量来建立围岩渗透系数与体积应变之间的关系,以在分析中考虑围岩渗透特性的动态演化。具体而言,需在ABAQUS输入文件(INPUT文件)中,按一定的映射关系将围岩渗透系数(*PERMEABILITY)定义为与场变量相关(DEPENDENCIES)的变量参数;在此基础上,对于隧洞围岩内任一积分点,在任一增量步开始时,所编制的USDFLD用户子程序均会调用内置于ABAQUS中的应用程序GETVRM以获取其当前的应变状态并计算相应的体积应变,继而由公式(6)计算该积分点当前的渗透系数并依据上述围岩渗透系数与场变量之间的映射关系确定场变量的取值,从而在分析中实现围岩渗透系数随应变状态改变的动态演化。

3 有限元模型与计算方案

3.1 有限元网格模型及计算参数

某深埋高外水隧洞长16.67 km,沿洞轴线主要岩层为三叠系大理岩、砂板岩和绿片岩,最大埋深为2 525 m。隧洞断面形状为四心圆马蹄形,开挖洞径为13 m,自开挖边界沿径向至深部岩体10 m范围为阻水灌浆圈。以砂板岩洞段某断面为例,建立渗流-应力耦合有限元模型,模型采用带孔压自由度的四结点平面应变单元CPE4P,灌浆圈单元与其外侧围岩单元在两者交界面处共用结点,模型单元总数和结点总数分别为3 864和3 724。模型顶部压力水头为430 m,上覆岩层厚度为1 000 m。

采用基于Mohr-Coulomb屈服准则的弹塑性本构模型模拟围岩(含灌浆圈)的力学特性。图2为模型有限元网格剖分及边界条件示意图。根据地应力测试成果,初始地应力以自重应力为主,侧压力系数取为0.87[25]。表2列出了计算参数。

图2 有限元模型网格剖分及边界条件(单位:m)

表2 有限元模型计算参数

3.2 计算方案

本文主要研究岩石基质压缩对高外水隧洞围岩变形稳定性的影响,为分析高外水隧洞围岩的变形稳定性,需在渗流-应力耦合分析中模拟隧洞开挖,开挖引起的地应力释放荷载及外水内渗力学作用由围岩承担。采用的分析步骤为:(1)模拟隧洞初始地应力场和孔隙压力场,位移清零;(2)模拟隧洞岩体开挖,释放开挖荷载,开挖边界结点孔隙水压力设为0 。此外,为揭示高外水隧洞围岩应力变形状态随岩石基质可压缩性的变化规律,在表2所列参数的基础上,将其中的孔压修正系数α分别调整为1.0(即不考虑岩石基质压缩)、0.65和0.50,并开展相应的渗流-应力耦合分析。

4 结果与分析

4.1 渗流场

图3给出了隧洞开挖后部分围岩(图2(b)所示区域)的孔隙水压力分布。由图3可以看出,由于隧洞开挖导致的排水作用,开挖边界处孔隙水压力降为0,自开挖边界处沿径向至深部岩体,围岩(含灌浆圈岩体)内的孔隙水压力逐渐增大;由于灌浆圈岩体具有较强的抗渗能力,灌浆圈岩体内的水力梯度明显高于其外侧岩体。

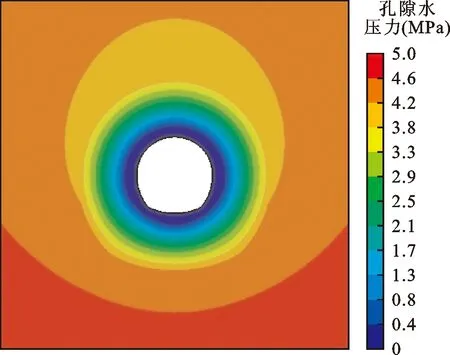
图3 隧洞开挖后部分围岩的孔隙水压力分布

图4给出了隧洞开挖后自开挖边界特征点沿径向至深部岩体的渗透系数分布。由图4可以看出, 在不同特征点处,渗透系数均呈现出自开挖边界至深部岩体逐渐减小的变化规律,且距开挖边界越近,变化越显著,合理体现出了隧洞围岩变形对其渗透性能的影响。

图4 隧洞开挖边界特征点沿径向至深部岩体的渗透系数分布(单位:m)

图5给出了灌浆圈岩体自开挖边界沿径向孔隙水压力分布。由图5可以看出,距离开挖边界2 m范围内灌浆圈岩体的孔压径向变化率明显小于外侧岩体,原因在于该范围内灌浆圈岩体的渗透系数与其初始值相比明显增大。

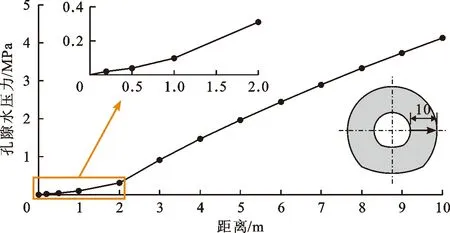
图5 隧洞灌浆圈岩体自开挖边界沿径向孔隙水压力分布(单位:m)

4.2 围岩变形稳定性

图6给出了隧洞开挖后围岩位移矢量和等效塑性应变分布。由图6可以看出,在地应力释放和外水内渗的共同作用下,围岩产生了指向隧洞中心的位移,距隧洞开挖边界越近,围岩位移越大,极值为17.2 mm,位于隧洞两侧墙中心部位(图6(a));临近开挖边界的灌浆圈岩体内出现了塑性屈服现象,塑性区总体呈现出环状分布特征(图6(b)),平均径向深度Dp为3.22 m,约为洞径的24.77%,未超过设计锚固深度4.5 m,围岩变形稳定性基本可以得到保证。

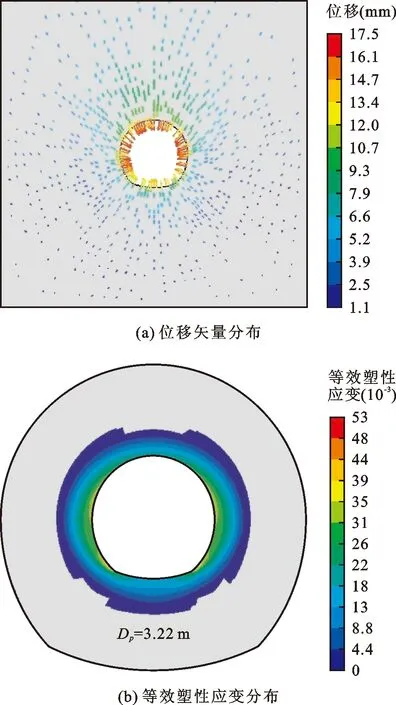
图6 隧洞开挖后围岩位移矢量和等效塑性应变分布

4.3 岩石基质压缩效应

图7给出了孔压修正系数α不同取值下隧洞开挖后自开挖边界特征点处沿径向至灌浆圈的渗透系数分布。由图7可以看出,对于不同的α取值,灌浆圈岩体内同一位置处具有不同的渗透系数,且距开挖边界越近,差异越大,当α取为0.83、0.65和0.50时,开挖边界特征点处的渗透系数分别为6.83×10-7、7.65×10-7和8.42×10-7m/s,较不考虑岩石基质压缩(α=1.0)时分别增大了11.60%、24.99%和37.46%,表明岩石基质压缩直接影响着高外水隧洞外水内渗过程,并将通过渗流-应力耦合对隧洞围岩的变形稳定性产生影响。

图7 α不同取值下隧洞灌浆圈岩体渗透系数径向变化

图8给出了隧洞开挖边界特征点径向位移与孔压修正系数α之间的关系曲线。由图8可以看出,随着岩石基质可压缩性的提高,隧洞变形呈现逐渐增大的变化规律,α=0.50时的开挖边界特征点径向位移较不考虑岩石基质压缩(α=1.0)时增大约10.03%,出现上述现象的主要原因是在其他条件相同时,高外水隧洞围岩的岩石基质可压缩性越大,则源于地应力释放的开挖不平衡力越大,表明岩石基质压缩对高外水隧洞围岩变形稳定性不利,在计算分析中忽略岩石基质压缩将得出偏于危险的结果。

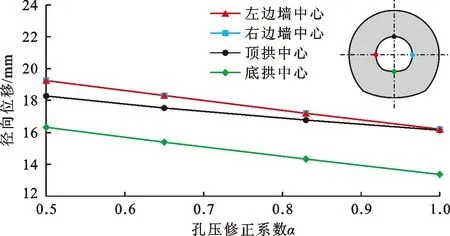
图8 隧洞开挖边界特征点径向位移与α的关系曲线

图9给出了α取值为1.0、0.65和0.50时的围岩等效塑性应变分布。结合图9和图6(b)可知,随着α值的减小,围岩塑性损伤区范围逐渐增大,当α取为0.83(图6(b))、0.65和0.50时,塑性区平均径向深度Dp分别为3.22、3.32和3.43 m,是不考虑岩石基质压缩(Dp=3.13 m)时的102.88%、106.07%和109.58%。上述结果与围岩应力变形的变化规律相协调,进一步表明岩石基质压缩会对围岩的变形和稳定性产生不利影响。因此,为保障高外水隧洞变形稳定,应在分析中考虑岩石基质压缩效应。

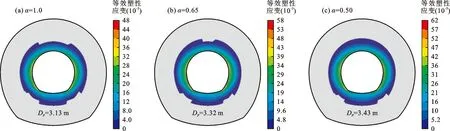
图9 α不同取值下隧洞围岩等效塑性应变分布

5 讨论

高外水隧洞修建于饱和岩体中,其围岩受力变形特征及稳定性与开挖引起的渗流场与应力场之间的相互作用密切相关[26]。通过开展模拟开挖过程的渗流-应力耦合分析,可以较为准确地获取高外水隧洞在开挖前后的渗流场和应力变形场,从而为合理评估其围岩变形稳定性提供定量依据[27]。由于岩石材料的骨架基质压缩系数与其宏观压缩系数处于同一量级,需在饱和岩体渗流-应力耦合分析中考虑岩石的基质压缩性[28]。本文通过开展孔压修正系数不同取值下的深埋引水隧洞渗流-应力耦合分析,系统分析了岩石基质压缩对高外水隧洞变形稳定性的影响,结果表明岩石基质的可压缩性越大,则隧洞围岩变形和塑性区范围越大。白林等[29]研究了岩石基质压缩性对地层沉降量的影响,发现岩石基质的可压缩性越大,地层沉降量越大,这可与本文的研究结论相互印证。

开挖不平衡力是导致隧洞等岩体地下洞室围岩变形失稳的主要力源。本文研究表明,如果在高外水隧洞变形稳定性分析中不考虑岩石基质压缩效应,则会低估饱和岩体的有效应力,致使开挖不平衡力计算值小于真实值,从而使得分析结果偏于危险。上述发现对于合理分析高外水隧洞变形稳定性具有重要意义。需要指出的是,高外水隧洞变形稳定性基质压缩效应的强弱不仅取决于岩石基质可压缩性的大小,亦与初始地应力场和地下水位相关。后续可在同时考虑上述因素变化的情况下进一步开展相应的研究工作。