狭窄型水库不同滑速滑坡对涌浪特性及工程影响
2023-11-13贺翠玲李鹏峰荆海晓万克诚段军邦
贺翠玲, 李鹏峰, 张 智, 荆海晓, 万克诚,4, 段军邦
(1.陕西省水生态环境工程技术研究中心, 陕西 西安 710065; 2.中国电建西北勘测设计研究院有限公司,陕西 西安 710065;3.西安理工大学, 西北旱区生态水利国家重点实验室, 陕西 西安 710048; 4.国家能源水电工程技术研发中心高边坡与地质灾害研究治理分中心, 陕西 西安 710065; 5.黄河上游水电开发有限责任公司, 青海 西宁 810000)
1 研究背景
库区滑坡涌浪是一种破坏性极高的次生灾害,高速失稳体可在库区产生巨大的涌浪,传播至坝前可能会翻越坝体,甚至会造成坝体溃决,对挡水建筑物及库区居民造成严重威胁[1-3]。历史上发生过较大的滑坡涌浪事故,如:1958年美国阿拉斯加州的Lituya Bay滑坡,涌浪波最大爬坡高度达到524 m[4];1963年意大利瓦伊昂水库滑坡造成约2 000人死亡[5];我国三峡库区也是滑坡涌浪灾害发生较多的区域,据不完全统计,三峡库区共监测到滑坡3 028处,其中2003年7月13日千将坪滑坡产生的涌浪波在对岸爬高超过30 m,在库区传播距离超过10 km,造成了巨大的经济损失[6-8]。因此,滑坡涌浪生成过程、涌浪波在库区演变及岸坡爬坡过程的精准预测对防止水库漫坝、降低滑坡涌浪灾害至关重要。
为了对滑坡涌浪灾害问题进行预警和风险评估,众多学者针对滑坡涌浪生成过程和浪高预测开展了细致的研究。黄智敏等[9]模拟了乐昌峡水库鹅公带滑坡体不同滑速工况对浪高、漫坝水量及动水压强的影响;中国水利水电科学研究院提出浪高预测中的主导因素为滑坡体入水的速度和滑坡体的方量,并以此假设为基础建立了浪高预测公式[10];潘家铮[11]根据条分滑坡体提出了计算滑坡涌浪初始浪高的方法,后续有学者用潘家铮方法和水科院经验公式法论证了坡脚压脚措施对降低涌浪高度的效果[12];Clous等[13]基于能量转换,研究了散粒体滑坡产生的涌浪波波能问题;Evers等[14]基于理论分析研究了涌浪波在时间和空间上的脉冲性,探讨了涌浪波在传播过程中的震荡危害;曹婷等[15]利用物理模型试验研究了滑坡体形状对涌浪爬高的影响;肖莉丽等[16]针对三峡库区滑坡涌浪问题建立了1∶200的物理试验模型,研究了近源区多因素对首浪高度的影响;黄锦林等[17]建立了1∶150的乐昌峡水库物理模型,研究了滑坡体滑速对涌浪特性的影响,并将实验结果与多个经验公式进行了对比;马鑫磊等[18]比选了在20多个典型滑坡涌浪实际灾害评价中用到的国内外主流滑坡涌浪浪高预测方法,并指出了主流评价方法的不足;黄宇云等[19]应用三维流体模拟软件Fluent,假定长岭皮水库滑坡体为颗粒流,研究了滑坡体不同体积与坝址最大浪高的关系。
综上所述,现有研究主要针对宽广水域或无坝河段的滑坡涌浪问题,对于狭窄型河道水库而言,其涌浪生成、传播甚至于爬坡的影响因素更加复杂,因此宽广水域滑坡涌浪规律未必能反映出近坝库区狭窄河道的滑坡涌浪规律。此外,流体动力学三维数值模拟软件Flow Hydro在滑坡涌浪问题研究中的应用性能也需进一步研究和评价。因此,本研究针对黄河羊曲水电站狭窄库区1#变形体失稳后不同滑速产生的涌浪灾害问题,基于Flow Hydro模拟软件分析库区滑坡涌浪的产生、发展和传播过程,进一步探讨了滑坡入水速度对涌浪特征的影响以及对工程的危害,以期为大坝的安全提供技术支撑。
2 数值模型及验证
羊曲水电站位于青海省海南藏族自治州兴海县与贵南县交界处的黄河干流上,属黄河上游水系。工程规模为一等大(1)型工程,坝顶高程为2 721 m,防浪墙高度为1.2 m,水库正常蓄水位为2 715 m[20]。通过地质调查发现,H1滑坡体位于距坝轴线约1.2~2.0 km的坝前左岸,1#变形体位于坝址上游左岸,其上游侧边界与H1滑坡相邻,下游边界距坝址约750 m,变形体平面上呈不规则扇形,前缘宽度为710 m,后部较窄部位宽度约为100 m,变形体平均厚度为25 m,体积约为500×104m3,该变形体具有明显的强倾倒层和滑移拉裂层。滑坡体所处位置库区狭长,其上游和坝前河道宽广,具有传播方向上的二维特征和传播变形方向上的三维特征。因此,本研究建立基于Flow Hydro的三维数学模型。
2.1 数值模型原理
滑坡涌浪问题涉及复杂的流体和固体强耦合过程以及流体飞溅和固体破碎变形。因此,流体的基础三维特性通过求解三维Navier-Stokes方程获得,在此基础上进一步耦合紊流RNG模型来实现流体复杂变形的模拟[21],流体表面识别采用改进的VOF(volume of fuid)技术[22],其控制方程如下。
连续性方程:
(1)
动量方程:
(2)
式中:u、v、w分别为x、y、z方向的速度,m/s;Ax、Ay、Az分别为x、y、z方向的水流面积,m2;t为时间,s;ρ为水体的密度,kg/m3,模型材料属性默认加载值为1 000 kg/m3;p为压强,Pa;RSOR为源项;VF为单元网格体中流体的体积分数,水气交界面取值为0.5,(Gx,Gy,Gz)为作用在单位质量流体微元的重力,N; (fx,fy,fz)为作用在单位质量流体微元的黏性力,N;Uw=(uw,vw,ww)为源项的速度,m/s;us,vs,ws为相对速度,m/s。
紊流模型为RNG模型:
DiffT-εT
(3)
式中:DiffT为紊流扩散项;PT为紊流动能产生项;GT为浮力产生项;kT为紊流动能;εT为紊流耗散项。
对于滑坡与水体的流固耦合过程,只要能够准确描述滑坡体运动过程,将该过程体现在网格上,通过VOF在网格上识别固体区就可实现滑坡体与水体的耦合。因此选用Flow Hydro中稳定性和精度最为突出的GMO(general moving object)模型来描述滑坡运动,由每个时刻网格的变化来逐步更新滑坡体的位置,采用VOF法捕捉每个时刻的水气交界面、固液交界面及固气交界面[23-24]。
2.2 数值模型建立
研究范围的选取和模型网格的划分需要考虑计算成本、计算精度及区域内浪高干扰等多方面因素,本研究中涌浪模型下游侧选取到羊曲水电站坝下游,只要不影响波浪在坝身的爬高即可;上游侧选取到羊曲水电站坝上游地形开阔区域,该区域可以使得波浪尽可能衰减,减小反射波对观测值的干扰;左、右岸范围包含滑坡体即可。按照上述原则建立的滑坡涌浪三维数值模型区域及边界条件如图 1所示。图 1中具体的模型范围为:1#变形体上游侧边界向上游延伸1 km,下游至羊曲水电站大坝;左岸沿河地形模拟至3 000 m高程,右岸模拟至2 800 m高程。模型网格设计方案中,沿x方向(宽度方向)宽度为1 500 m,沿y方向(长度方向)长度为3 600 m,沿z方向(高度方向)高度为450 m;网格尺寸在x方向和y方向为5.0 m,z方向为2.5 m,网格总数为4 860×104。在边界条件设置方面,左岸、右岸、上游及河床底部均设置为墙边界(Wall),下游设置为开边界,漫坝水体自由出流(Outflow),大坝顶部设置通量面,用来监测漫坝水体通量,顶部边界设置为大气压(Pressure=0)。
2.3 数值模型验证
为了对数值模型进行验证,本研究按重力相似准则设计建立几何比尺为1∶200的物理模型,根据《水电水利工程滑坡涌浪模拟技术规程》(DL/T 5246—2010)相关要求[25],模型滑坡体满足几何相似和块体的比重相似,河道和岸坡满足阻力相似。图2为本研究所建立的羊曲水电站滑坡涌浪试验模型;图3为模型试验观测设备布置图。滑坡体通过不同尺寸的混凝土块组合模拟,滑车通过多铰链的刚板组合实现;涌浪时程变化数据的记录采用CBG03智能浪高仪,沿程总共布置16个浪高仪(Ob1~Ob16);滑坡体下滑速度、滑坡区域涌浪爬高及建筑物前涌浪爬高采用高速摄像机采集,漫坝水量使用量筒测量。
在1#变形体滑坡体积为100×104m3、滑坡启动高程为2 755 m(试验入水速度为14.05 m/s)、水库正常运行水位为2 715 m条件下,进行数值模拟和模型试验观测,为了实现数值模拟与模型试验中滑坡体的相似性,模拟时将滑坡体切分成小块。选取滑坡处(浪高仪Ob8)和坝前(浪高仪Ob3)两个测点,通过涌浪浪高模拟数据与试验实测数据比较来验证数值模型的准确性,图4为该两个测点涌浪浪高时程变化的模拟值与试验值对比。从图4可以看出,两个测点的涌浪浪高和相位基本一致,首波和次生波的模拟值与试验值吻合精度高,而尾波吻合精度较差。分析其原因:由于模型试验的实际入水速度为14.05 m/s,与目标速度或者数值模拟给定的入水速度15 m/s有偏差,这两种速度的差异会反映到后续涌浪浪高和波长上;此外,数值模型上游区域未做消波处理,而物理模型试验中在上游加设了溢流堰来防止反射波的影响,各因素叠加导致后续波的拟合效果较差。但后续涌浪浪高较小,对建筑物的影响相对于首波和次生波来说可以忽略。综合分析认为,该数值模型计算精度满足要求,可用于后续研究。
3 结果分析与讨论
在水库位为正常运行水位2 715 m条件下,分析讨论1#变形体滑坡方量为100×104m3的矩形断面分别以5、10、15、20、25、30及35 m/s的入水速度刚性整体下滑时产生的初始涌浪高度及对岸坡和建筑的影响。滑坡涌浪数值模拟工况见表1。
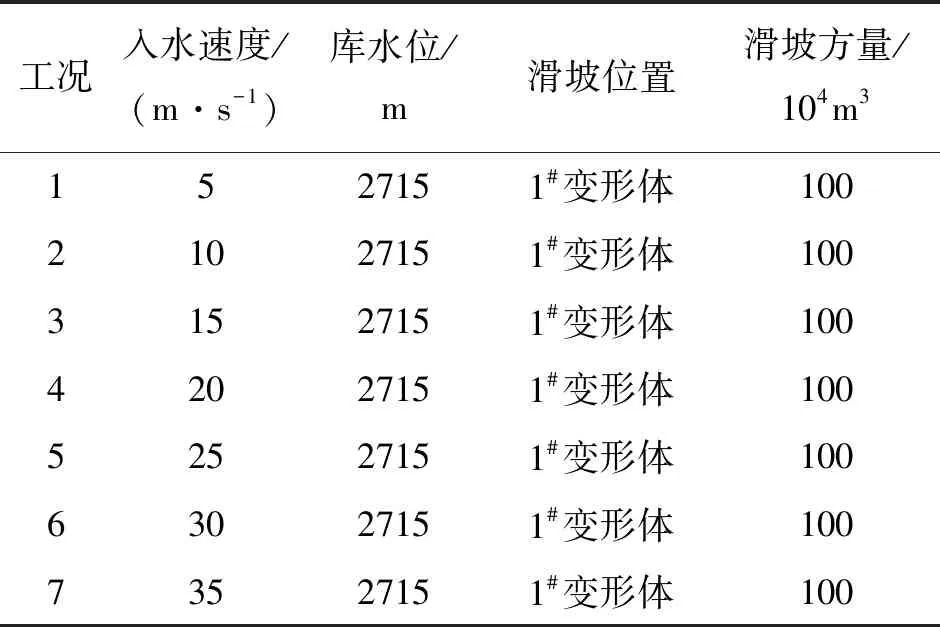
表1 羊曲水电站库区滑坡涌浪数值模拟工况
图5为工况4(入水速度为20 m/s)滑坡涌浪流场变化过程云图。由图 5可观察到,1#变形体所处位置的库区水面较为狭窄,滑坡体入水使得大部分水体被直接推向对岸,仅有少部分水体形成首波向上、下游河道传递(图5(b));滑坡体坍塌后的岸坡形成空缺,使水体开始后溃,后溃水体反射再次生成次生波(图5(c));起初滑坡体推向对岸的水体在重力作用下从对岸岸坡跌落,再次形成涌浪继续向上、下游传播(图5(d))。李世贵[6]、邓成进等[26]通过研究发现,滑坡入水产生涌浪后,波浪场呈半圆曲线向远端传递,但本研究中的涌浪生成过程具有明显的狭窄库区特性,地形严重影响了涌浪波的生成以及波场的反射和传播,因而无明显的圆形曲线传播规律。
图6为各工况滑坡处Ob8测点水面波浪高度(相对于库水位2 715 m的浪高)时程线模拟结果。由图 6可知,首波的波峰高度并不一定是最大的,某些情况下次生波的波峰高度最高,这是由于滑坡产生的波浪与对岸反射波叠加所致,在该过程中,涌浪波表现出明显的震荡性[27]。随着滑坡体滑速的增大,首浪浪高呈减小的趋势,这虽然与常规二维水槽试验的结果不同,但与模型试验观测结果一致[28]。分析产生这一结果的原因可归纳为两个方面:一方面随着滑坡体速度的增大,能量传递到对岸岸坡导致涌浪爬坡高度增加,而纵向扩散减小;另一方面如果滑坡体速度过大,则首波传递到测点时涌浪并未成形,还在发展过程中。由图6还可看出,波速随着滑坡体滑速的增大而增大,滑速为35 m/s时形成的滑坡涌浪最先传播到测点,滑速为5 m/s时的滑坡涌浪最后传播到测点。各工况波峰高度均在坝顶高程附近,如果涌浪在传播过程中衰减较小,就有可能发生漫坝。
图7为工况4坝前区域9个时刻的波场云图。由图7可以看出,该工况下会发生多次波散射,波场复杂。由于波反射和叠加作用,某些位置的波高可能高于入射波。图8为各工况坝前中部Ob3测点水面波浪高度(相对于库水位2 715 m的浪高)时程线模拟结果。由图8可知,首先,各滑速生成的涌浪波在从Ob8测点传至Ob3测点过程中并没有出现大幅度衰减(与图 6对比分析)。其次,各工况的首波波高并非最大,最大波高为120~125 s出现的第4个波峰,这是由于坝前区域的多次波反射所致。此外,几乎所有工况生成的涌浪波均会出现漫坝现象,漫坝位置主要在左、右坝肩处。
图9为各工况溢洪道进口(坝左)、坝中及电站进水口(坝右)处的次生涌浪浪高变化规律。从图 9中可以看出,当滑坡体入水速度从5 m/s增加到10 m/s时,坝前浪高明显增大;当入水速度在10~35 m/s之间时,浪高保持缓慢增加趋势。工况1~7建筑物前浪高大小排序如下:溢洪道进口处(坝左)>电站进水口处(坝右)>坝中,坝前水面呈两端高中间低的态势。
图10为各工况滑坡涌浪引起的漫坝流量时程线。由图10可以看出,所有工况都会发生多次漫坝,与前述坝前浪高分析一致。首波对漫坝流量的贡献很小,漫坝流量的第一个峰值出现时刻在100 s左右,但是首波到达坝前的时刻约为40 s,其时间差距较大,这表明滑坡生成的涌浪波首波不一定是决定灾害等级的关键性指标,涌浪波后续的传播和散射也非常重要,在实际工程中必须进行准确预测。图11为各工况漫坝水量统计结果。图11表明,漫坝水量随着滑坡入水速度的增大而增加。
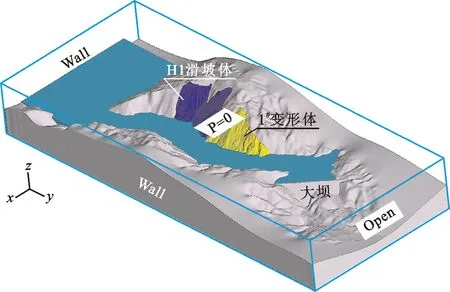
图1 滑坡涌浪三维数值模型区域及边界条件示意图

图2 羊曲水电站库区滑坡涌浪试验模型
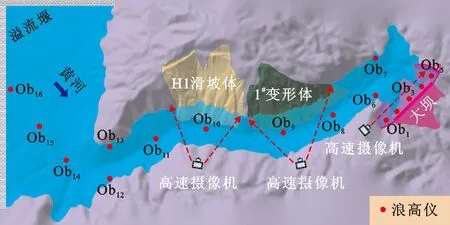
图3 羊曲水电站库区滑坡涌浪模型试验观测设备布置

图4 滑坡处和坝前两测点涌浪浪高时程变化的模拟值与试验值对比

图5 工况4(入水速度20 m/s)滑坡涌浪流场变化过程云图
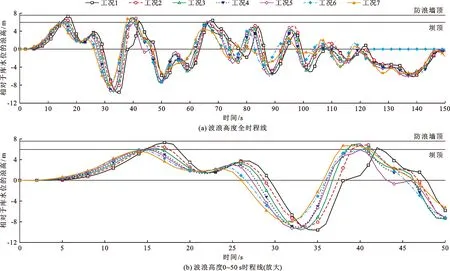
图6 各工况滑坡处Ob8测点水面波浪高度时程线

图7 工况4(入水速度20 m/s)坝前区域9个时刻的波场云图
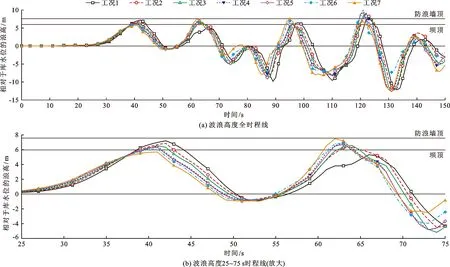
图8 各工况坝前中部Ob3测点水面波浪高度时程线

图9 各工况建筑物前次生涌浪浪高变化规律

图10 各工况滑坡涌浪引起的漫坝流量时程线
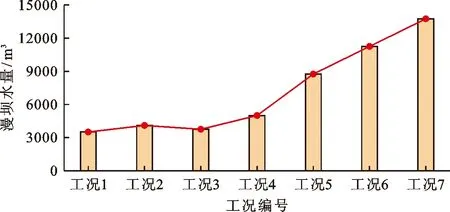
图11 各工况漫坝水量统计图
4 结 论
在本研究中,使用三维数值模型模拟了黄河上游羊曲水电站库区1#变形体滑坡涌浪的产生、传播、爬高和漫顶全过程。通过1∶200比尺的物理模型进行涌浪时程线的比较,验证了数值模型的有效性,模拟分析了滑坡入水速度对波高和漫坝过程的影响。得出以下结论:
(1)物理模型验证表明,本研究所建立的数值模型是准确的,该数值模型对首波和次生波的生成、传播及漫坝过程均能准确刻画。
(2)随着滑坡入水速度的增加,首波波峰高度减小,而且首波波峰并不总是最高的,这与滑坡涌浪生成过程及库区地形影响有关。
(3)在滑坡生成的涌浪向大坝传播过程中,首波没有发生明显的衰减,传播到坝址处时,溢洪道进口(坝左)波高最高,电站进水口(坝右)波高次之,坝中波高最小。
(4)滑坡体入水速度在5~35 m/s时,涌浪波传播到坝前均会发生漫顶,但首波对漫坝总水量的贡献很小。此外,漫坝流量峰值出现的时刻远滞后于首波到达坝前的时刻,这是由大坝附近波浪的多次散射所致,这一现象在实际工程中必须引起重视。
