基于MSVD-AE的航天器电源系统故障检测方法
2023-11-13朱慧斌何章鸣王炯琦王宇昂周海银
朱慧斌, 何章鸣, 王炯琦, 王宇昂, 周海银*
1. 国防科技大学, 长沙 410073
2. 中国人民解放军31002部队, 北京 100094
0 引 言
电源系统被称为航天器的心脏,系统的好坏直接影响航天器的寿命和在轨性能[1-3].据统计,在航天器在轨运行过程中的500多次故障,14%是电源系统故障,电源系统的故障率在航天器故障中排名第二[4].由于航天器具有很高的政治、军事和经济价值,因此,航天器的任何异常都会影响航天器的正常运行,甚至报废,造成重大损失[5].因此,及时有效检测航天器电源系统(spacecraft power subsystem,SPS)的异常变化将提高航天器主动检测和识别能力,为航天器的安全稳定运行提供可靠的决策支持.
目前,故障的检测方法可以分为基于模型的故障检测、基于知识的故障检测和基于数据驱动的故障检测.然而,由于SPS工作环境复杂性以及SPS存在的多模块非线性非平稳等特性,使得基于模型和基于知识的故障检测方法难以准确有效的检测SPS故障.相反,能够大量的获得SPS的遥测数据,因此,基于数据驱动的SPS故障检测具有更高可行性[6].然而,基于数据驱动的SPS故障检测存在以下问题:
1)遥测数据被噪声污染.由于航天器所处环境的复杂性,航天器不可避免的受到各种外界因素的影响,如太阳风暴、空间辐射、宇宙射线、温度波动等,进而影响遥测数据的质量.对于以数据为核心的故障检测算法,数据质量的好坏直接影响后续诊断方法的计算效果.因此,如何有效去除数据中含有的噪声,是保证检测算法有效的前提.
2)遥测数据无故障标签.一方面,航天器在轨运行期间,SPS会受到各种各种因素的影响,出现未知故障;另一方面,SPS含有多个闭环子系统,使得遥测数据难以及时反映故障信息.因此,如何有效检测无标签数据的故障信息,是保证检测算法有效的基础.
目前常用的信号处理方法有小波变换(wavelet transform,WT)[7-9]、经验模态分解(empirical mode decomposition,EMD)[10-11]等.CHEGINI等[12]提出了一种基于经验小波变换的振动信号去噪和轴承故障识别新技术,通过改进阈值函数对噪声主导模式进行去噪.WANG等[13]提出了一种基于双树复小波变换的振动信号去噪算法,结果表明所提出的去噪方法可以有效地去除噪声并尽可能保留有价值的信息.XIONG等[14]将EMD与度量准则相结合,过滤轴承加速度信号趋势和噪声.SAHU等[15]基于完全集成经验模式分解和自适应阈值方法,提出了一种用于滚动轴承早期故障诊断的改进的去噪技术,而后在两个轴承数据集上验证了方法去噪的有效性.虽然上述方法在工业数据集上得到了较好的应用,但是却很少应用于SPS中.另外,WT及其衍生算法需要事先获取信号的先验信息以选取合适的小波基.而EMD在分解过程中,会出现过包络、欠包络以及模态混叠等情况[16-19].这些都在一定程度上限制了上述方法的使用.
奇异值分解(singular value decomposition,SVD)也被应用于信号处理中[20-23].SHIN等[24]利用奇异值分解来去除确定性时序信号的加性噪声.GOLAFSHAN等[25]采用基于Hankel矩阵的SVD去噪方法消除背景噪声,提高故障检测的可靠性.然而,传统SVD算法在处理信号数据时,其本质上是在相同的分辨率和层次空间上进行[26].因此,ZHAO等[27]借鉴WT思想,提出了多分辨奇异值分解(multi-resolution singular value decomposition,MSVD)算法,将SVD分解结果划分为不同的层次空间,通过SVD方法将解析信号分解为若干个不同分辨率的近似信号和细节信号.目前该方法主要用于轴承等机械信号的特征提取,在信号去噪,特别是SPS遥测信号去噪方面还缺乏相关研究.
目前,由于计算机能力的增长和大量数据的积累,以支持向量机、神经网络等为代表的机器学习方法收到了广泛的关注,在故障检测领域得到了广泛的应用.SUO等[28]通过模糊贝叶斯风险提取SPS特征,而后结合支持向量机进行故障诊断.XIAO等[29]提出了一种基于深度学习的故障诊断方法用于航天器姿态控制系统.GANESAN等[30]利用卷积神经网络训练SPS的遥测数据,而后在NASA的先进诊断和预测试验台(advanced diagnostics and prognostics testbed,ADAPT)验证了算法的有效性.PRASAD等[31]采用马尔可夫转换场、递归图和频谱图等将ADAPT数据转换为图像,而后采用二维卷积神经网络对其进行分类,结果表明测试精度达87.5%.然而,这些算法都需要故障标签来求取模型参数,因此,无法检测无故障标签的SPS.
自编码器作为一种无监督的机器学习算法,能够通过构建残差阈值实现无故障标签的故障检测[32-33].因此,针对SPS遥测数据存在的噪声和无故障标签的难题,本文提出了基于多分辨奇异值分解和自编码器的航天器电源系统故障检测方法,通过MSVD降低噪声对遥测数据的影响,并分析了多分辨奇异值分解的去噪原理.而后通过自动编码器 (autoencoder,AE)对降噪后的无故障标签数据进行异常检测;最后,通过SPS数据验证了算法的有效性.全文组织结构如下.第一节介绍了多分辨奇异值分解的去噪方法,并进一步分析了该方法的去噪原理.第二节概述了自编码器的检测算法.试验结果将在第三节中展示和讨论.结论在第四节中讨论.
1 基于多分辨奇异值分解的去噪方法
1.1 奇异值分解
设x(n)为一维数据,其中n=1,2,…,N,N是信号x(n)的长度.依据相空间重构理论,信号x(n)的轨迹矩阵构造如下:
(1)
其中,L表示轨迹矩阵列数.假设A为实矩阵,则A的奇异值分解为
(2)
其中,U=[u1u2…uN-L+1]∈R(N-L+1)×(N-L+1),V=[v1v2…vL]∈RL×L为正交矩阵.Σ=[diag{σ1,σ2,…,σl}O]∈R(N-L+1)×L,l=min((N-L+1),L),σ1≥σ2≥…≥σl为矩阵A的奇异值,O∈R(N-L-l+1)×L为零矩阵.通过去除式(2)中的零奇异值,A的SVD可以表示为
(3)
其中,ui和vi分别为U、V的第i列向量.
1.2 多分辨奇异值分解
目前大多利用SVD的正交性或降维来解决具体问题[34],信号经SVD分解后所得的结果在本质上都属于同一个层次的矢量空间,该矢量空间是由SVD分解后得到的左正交矩阵的行矢量所张成的,或者是右正交矩阵的列矢量所张成的.因此,信号SVD处理后的结果都是一种处于在同一层次空间、同一分辨率上.针对上述问题,ZHAO等[27]在借鉴小波变换思想的基础上提出了MSVD算法,将信号分解到不同的层次空间.
信号x(n)为一维数据,其中n=1,2,…,N,N是信号x(n)的长度.将信号x(n)的轨迹矩阵构造为
(4)
设已经进行了j-1次分解,得到j-1个SVD近似信号Aj-1=[xj-1,1…xj-1,N],构造轨迹矩阵为
(5)
对其进行SVD分解
(6)
其中,Uj=[uj1uj2],Uj∈R2×2,Vj=[vj1…vj(N-1)],Vj∈R(N-1)×(N-1),Σj=[diag{σaj,σdj}O],σaj、σdj分别为第j次分解得到的近似奇异值和细节奇异值,则近似矩阵Haj和细节矩阵Hdj表示为
(7)
其中,uj1,uj2∈R2×1,vj1,vj2∈R(N-1)×1.采用奇异谱分析中的对角平均法[36],将近似矩阵Haj转化为SVD近似信号Aj
(8)
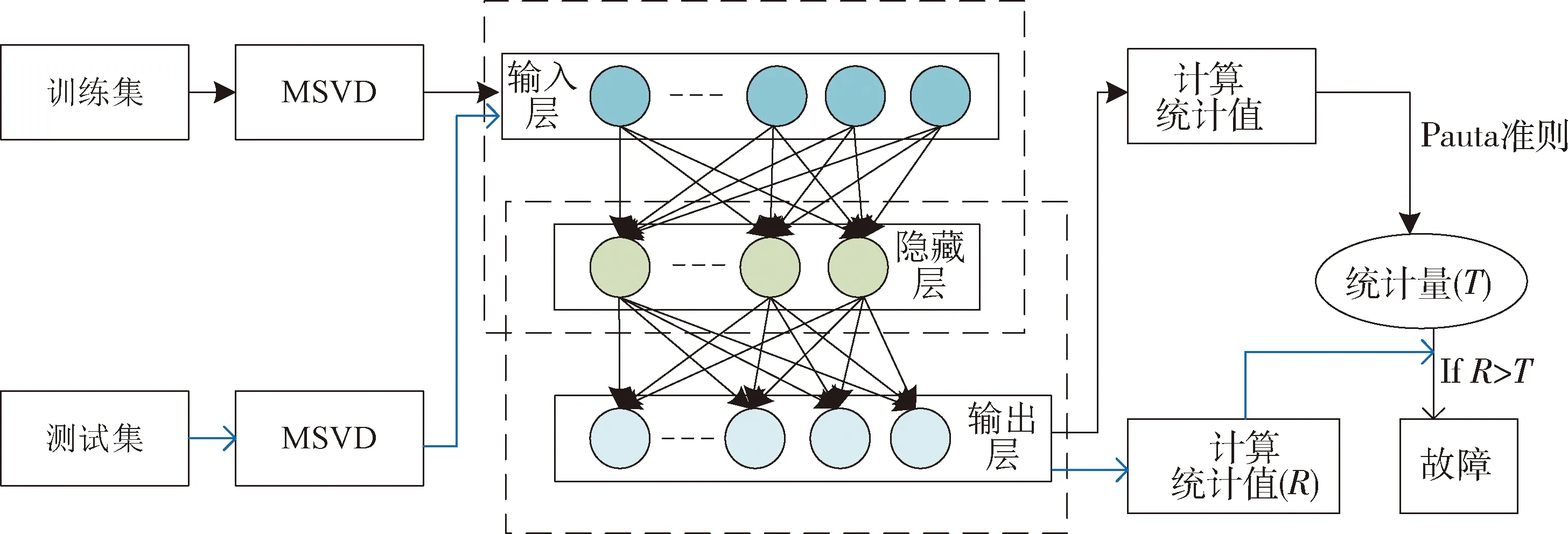
其中,xj,1,…,xj,N为近似矩阵Haj中的元素.对信号x(n)多次迭代并舍去细节矩阵信息,即可达到信号去噪的目的.多分辨奇异值分解结构如图1所示.

图1 MSVD分解结构示意图
1.3 多分辨奇异值分解去噪分析
与奇异值分解去噪原理相同,MSVD同样是利用信号与噪声在奇异向量上投影值的不同来去除噪声.设含噪声的离散信号x(n)可以表示为
x(n)=s(n)+ξ(n)
(9)
其中,s(n)为实际信号,ξ(n)为噪声,n=1,2,…,N,N是信号x(n)的长度.MSVD中的轨迹矩阵下一行矢量仅比上一行矢量滞后一个数据点,因此轨迹矩阵的两个行向量是高度相关的,因此较大的奇异值主要反应信号的信息,此时保留较大奇异值舍去较小奇异值即可有效去除信号噪声.另外,由Tanken定理可知[37-38],时间序列通过坐标延迟即可重构一个与原系统拓扑意义下等价的相空间.因此,测量信息的轨迹矩阵反映了测量系统在相空间中的状态.若将轨迹矩阵的列向量视为张成相空间的向量,则轨迹矩阵的行向量为不同时间下系统在相空间中的状态点.多个轨迹矩阵的行向量反映了系统在相空间中的运动轨迹.因此,在MSVD中的轨迹矩阵是相空间上延迟时间为1的两个状态点.对轨迹矩阵进行奇异值分解,在左奇异向量张成的二维空间,由于仅有两个状态点,因此,数据主要投影在一个坐标轴上.因此,舍弃较小奇异值对应的细节矩阵,对近似矩阵进行重构得到去除部分噪声的近似信号.而后对近似信号再次重复上述过程,由于再次构造的轨迹矩阵是以近似信号为基础,其所构成的相空间是原信号所构成相空间的其近似,因此,迭代奇异值分解能够在不同层次,多个维度去除信号噪声.
1.4 去噪评价指标
本文采用信噪比和平滑度两种去噪评价指标评价信号的去噪效果.信噪比的表达式为
(10)

(11)
计算所得的信噪比越大,平滑度越小,算法的去噪效果越好.
2 基于自编码器的故障检测
2.1 自编码器


图2 自动编码器架构(m δi=fθ(xi)=φf(wTxi+b) (12) (13) 其中,φg为解码器网络的激活函数,θ′={w′,b′}为解码器网络的训练参数.为尽可能地重建原始输入,AE的优化目标是将输入样本与重建样本之间的误差最小化 (14) 本研究中采用均方根误差计算统计量 (15) 由于缺乏异常标签,异常阈值的定义较为困难.本文采用3σ准则选取检测阈值.本研究中采用误报率(false positive rate,FPR)和准确率(accuracy,ACC)对所提出的方法进行评估.Fpr和Acc率的计算公式如下: (16) (17) 其中,Fp为实际为错误但被判断为正确的个数,Tn为判断正确的个数,N为样本的总数.故障检测流程图3所示. 图3 故障检测流程图 目前,大部分航天器电源系统采用太阳电池阵和蓄电池组结构.如图4所示,SPS主要由太阳能电池阵列、蓄电池组、充电调节器、放电调节器、分流调节器等部分组成[39-40]. 图4 航天器电源系统示意图 当航天器运行至光照期时,太阳电池阵负载航天器的用电需求,并对蓄电池充电,多余的电流通过分流器分流.当航天器从光照期过渡到地影期时,光照逐渐减弱,太阳电池阵和蓄电池同时负载供电,此时,控制部分只有放电调节器工作.当航天器运行至地影期时,蓄电池负载供电,太阳电池阵不工作. 虽然SPS上有许多可以反映SPS工作状态的传感器,但从SPS工作状态可以看出,电流始终是反映SPS工作状态的最为重要的参数之一,因此,本文选取电流遥测数据的来监控SPS运行情况. 本研究中所用的MATLAB 版本为R2020a.本研究中MSVD迭代4次.为验证MSVD算法的有效性,本研究选取了小波变换和经验模态分析这两种常用的信号去噪算法进行对比.其中小波变换的小波基为“db4”,分解3层.自编码器的编码器所用激活函数为‘satlin’,解码器所用的激活函数为‘logsig’.通过遍历确定AE、WT+AE、EMD+AE、MSVD+AE的最优隐藏层数分别为200、251、288和251,自编码器其他参数为MATLAB中自编码函数的默认值. 如图5所示,本文的试验验证数据为某在轨航天器电源系统的遥测数据.从图5中可以看出,遥测电流信号存在波动.这是由于SPS中的充电调节、放电调节以及分流调节等控制都会对电流产生影响,因此,遥测电流信号具有较强的波动性. 图5 航天器电源系统遥测电流曲线 SPS在2020年3月份左右发生故障,因此,本文选取2020年2月15日到2020年3月18日的航天器电流遥测数据为测试数据.选取航天器运行平稳的17年数据作为训练集,训练集数据为2017年2月15日到2017年3月18日航天器电流遥测数据.MSVD仅需几次迭代就能达到很好的去噪效果[41]. 去噪结果如图6和表1所示.航天器一年四季在轨道上运转,随着季节的变化,航天器接受太阳光照的角度、强度和时间均有变化[42].从图中可以看出,小波去噪效果较差.这是由于在春分期间,蓄电池放电的深度会导致遥测电流出现较大的变化,而由小波变换原理可知,小波变换是通过选取适当的小波基函数对信号进行拟合.因此,当拟合信号出现较大变化时,需要更多的小波基函数进行拟合,导致小波处理后的信号具有一定的波动性.然而对于航天器而言,电流的波动可视为由充放电调节等控制扰动产生的噪声,从而导致小波去噪效果不够理想.另外,从图中可以看出,当遥测电流出现较大变化时,可以将开始变化点视作断点,使得EMD容易产生端点效应,扭曲在端点处的波形.从图中可以看出,MSVD并不存在上述问题,因此,MSVD相对具有更好的去噪效果,而表中的去噪评价结果也能很好地说明MSVD具有更好的去噪效果. 表1 不同算法的去噪结果 表2 不同算法的航天器电源系统故障检测结果 图6 不同算法去噪效果图 将去噪后的航天器电流遥测信息放入自编码器中进行检测,从图中可以看出,经MSVD去噪后的遥测信号具有更好的检测效果.从表中可以看出,MSVD+AE的Fpr和Acc分别是1.1%和98.8%,误报率很小.相比WT和END,本文所提算法具有更低的漏报率.因此,对于航天器电源系统,本研究所提算法具有相对更好的检测效果,能够及时有效的检测出SPS故障. 本研究围绕SPS在实际工作中遥测数据存在的故障检测难题,提出了基于多分辨奇异值分解和自编码器的航天器电源系统故障检测方法.针对具有波动性的遥测电流信号存在噪声的问题,将MSVD运用到遥测电流信号处理中,进而分析了MSVD的去噪原理,完善了MSVD理论.针对SPS故障无标签问题,将无监督的AE运用到SPS的故障检测中,结合拉依达准则构建统计量阈值.采用真实的在轨SPS遥测数据进行了试验验证,结果表明,所提算法具有更低的误报率和更高的检测率,能够很好的满足SPS故障检测需求.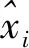
2.2 性能评估
3 试 验
3.1 航天器电源系统

3.2 试验环境及数据描述
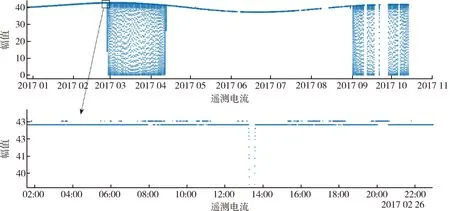
3.3 试验分析



4 结 论
