三明治结构挠性传动系统的自耦PID控制
2023-11-13曾喆昭
曾 鹏, 曾喆昭
长沙理工大学, 长沙 410076
0 引 言
三明治系统通常在2个动力装置之间存在一个非光滑非线性环节,例如带间隙的三明治系统就具有典型的非光滑非线性特征[1],而且是3阶或以上的非光滑非线性系统,因而该类系统的控制具有很大挑战性.在三明治结构挠性传动系统中[2],后端子系统会产生一个反馈信号输入至前端子系统,使得控制难度增大,比如汽车传动系统[2-4]、挠性关节机械手[5-8]、火炮炮塔传动系统[9-11]以及机炉控制系统[12-13]等.目前,该类系统的控制方法有:带有比例补偿的比例-积分-微分(proportional-integration- differential with proportional compensation, PID-P)复合控制方法[2],该方法响应速度快,然而不能有效抑制齿轮间隙带来的影响,且需要精确的模型来求解控制器参数;文献[3]针对带背隙的汽车传动系统提出了PID级联控制器,并且采用稳健的调谐策略[4],获得了良好的控制性能,然而其控制系统结构复杂、控制器参数较多;文献[5]将非线性前馈控制和线性奇异值摄动控制相结合,获得了良好的控制效果,然而其控制系统结构复杂,计算量大;文献[6]设计了比例-微分(proportional-differential, PD)边界控制器,通过在机械手的末端边界上进行基于指数收敛法的分布式参数边界控制,有效降低机械臂运动过程中的变形,然而控制器参数采用指数收敛法设计,计算量大;文献[7]针对间隙的空间机械臂,设计了含有间隙补偿的PD控制器,然而稳态控制精度不高,且驱动力矩一直存在较大抖动,无法消除间隙造成的影响,影响执行机构使用寿命;文献[9]设计了坦克火炮系统的非线性滑模控制器,以补偿背隙和参数漂移等非线性因素的影响,然而控制精度低;文献[10-11]分析了坦克火炮系统稳定精度较低的原因,并将惯性和机械间隙等负载波动归因于未知干扰,设计了自抗扰控制器,与传统的PID控制相比,具有更高的控制精度和良好的鲁棒性和适应性,然而控制器参数较多;文献[12-13]将PD控制和非光滑H∞控制相结合,有效解决了弱阻尼挠性模态和死区非线性带来的振动问题,然而其控制系统结构复杂,难以实际应用.
在三明治结构挠性传动控制系统中,为了有效解决现有控制方法存在控制系统结构复杂与计算量大的局限性,本文使用了ACPID控制方法[14-15].该方法科学阐明了传统PID控制中因无量纲比例增益会导致PID控制力输出与被控系统控制力输入之间的量纲冲突问题以及比例、积分和微分3个控制力的不协调控制问题,提出了一种基于速度因子的ACPID增益镇定规则或量纲换算规则,不仅有效解决了PID控制力与被控系统控制输入之间同一物理量的量纲匹配问题,而且理论上保证了功能各异的比例-积分-微分3个控制力在控制过程中体现出目标一致的协调控制机理,从而科学解决了PID增益鲁棒性差与抗扰动鲁棒性引起增益镇定困难的问题.此外,根据ACPID控制理论思想的“总扰动”概念,可以将任何复杂非线性系统等价映射为一个线性扰动系统[16-19],淡化了线性系统与非线性系统分类的概念,统一了线性与非线性系统的控制理论思想.考虑ACPID控制器结构简单,仅涉及到一个速度因子的镇定,因而便于三明治控制系统的实际应用.
1 问题背景
根据文献[2],带有齿轮结构的电动机驱动系统的原理如图1所示.

图1 三明治谐振系统
图中,Tm、ωm和Jm分别为电机的转矩、转速和转动惯量,Tc为轴输出转矩,Kc与Dc分别为传动轴刚度和阻力系数,TL、ωL和JL分别为负载转矩、转速和转动惯量,δ表示齿隙大小,σ为齿轮非线性环节的输出,ωg、Kg、Jg、Tg和Dg分别为从动齿轮的转速、刚度、转动惯量、力矩和阻力系数.
考虑齿隙效应的真实情况,齿轮的死区模型为
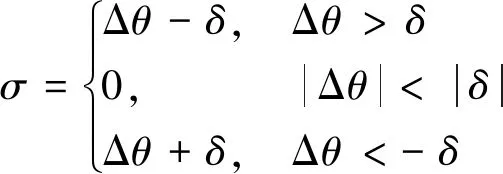
(1)
其中,Δθ=θm-θg为非线性环节的输入,θm为电机的旋转角度,θg为反馈回来齿轮的角度.
从电机输出转矩Tm到齿轮转矩Tg的动力学方程为
(2)
齿轮力矩为
Tg=Dg(ωm-ωg)-KgΔθ
(3)
同理,从齿轮力矩Tg到负载力矩Tc的数学模型为
(4)
其中,Tc=Dc(ωg-ωL)-Kc(θg-θL).
系统开环传递函数[2]为
(5)
其中,
(6)
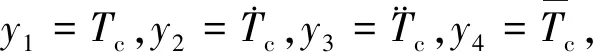
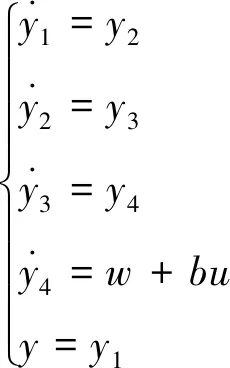
(7)
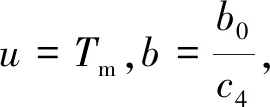
考虑到齿轮间隙的情形,因而系统(7)是一个4阶非光滑非线性系统.
2 ACPID控制系统设计
由于三明治谐振系统是一个4阶非光滑非线性的系统,为了使控制器的输出与被控对象的量纲匹配,因此要建立虚拟控制器[20].然而,文献[20]用自耦PI(auto-coupling proportional-integration, ACPI)控制器来控制4阶系统则需要3个虚拟控制器和一个实际控制器,为了进一步简化控制系统的结构,本文则使用一个自耦PD(auto-coupling proportional- differential, ACPD)虚拟控制器和一个ACPID实际控制器进行控制,其中,以ACPD虚拟控制器的输出作为ACPID控制器的虚拟期望指令.
2.1 ACPD虚拟控制器设计
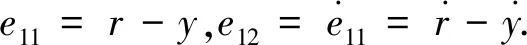
(8)
设y3的虚拟控制指令为y3d,则根据文献[20]中虚拟递推控制器以及文献[15]中ACPD控制理论的思想,定义下一个控制器的虚拟期望指令y3d为
(9)
其中,zc1>0是速度因子,|y3d|≤y3dm,y3dm为虚拟控制器输出的最大值.
2.2 ACPID控制器设计

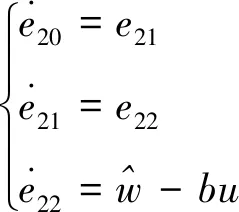
(10)

跟据文献[15]的ACPID控制理论思想,分别定义比例控制力、积分控制力与微分控制力如下:

(11)
受控对象的控制输入为
u=u2i+u2p+u2d
(12)
其中,zc2>0是速度因子,0≤u≤um,um为控制力u的最大幅值,|u2i|≤0.5um.
三明治系统转矩控制框图如图2所示.

图2 三明治系统转矩控制图
2.3 ACPID闭环控制系统分析

证明. 将式(9)所示的ACPD虚拟控制器代入受控误差系统(8),可得闭环控制系统为
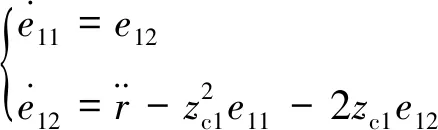
(13)
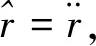
(14)
由式(14)可得系统传输函数为
(15)
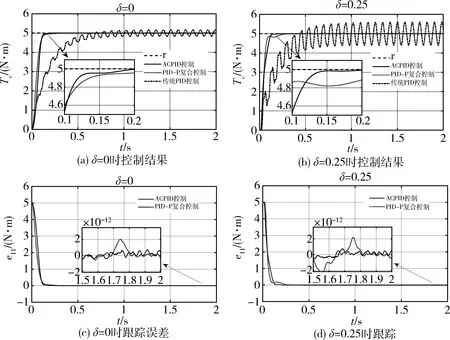
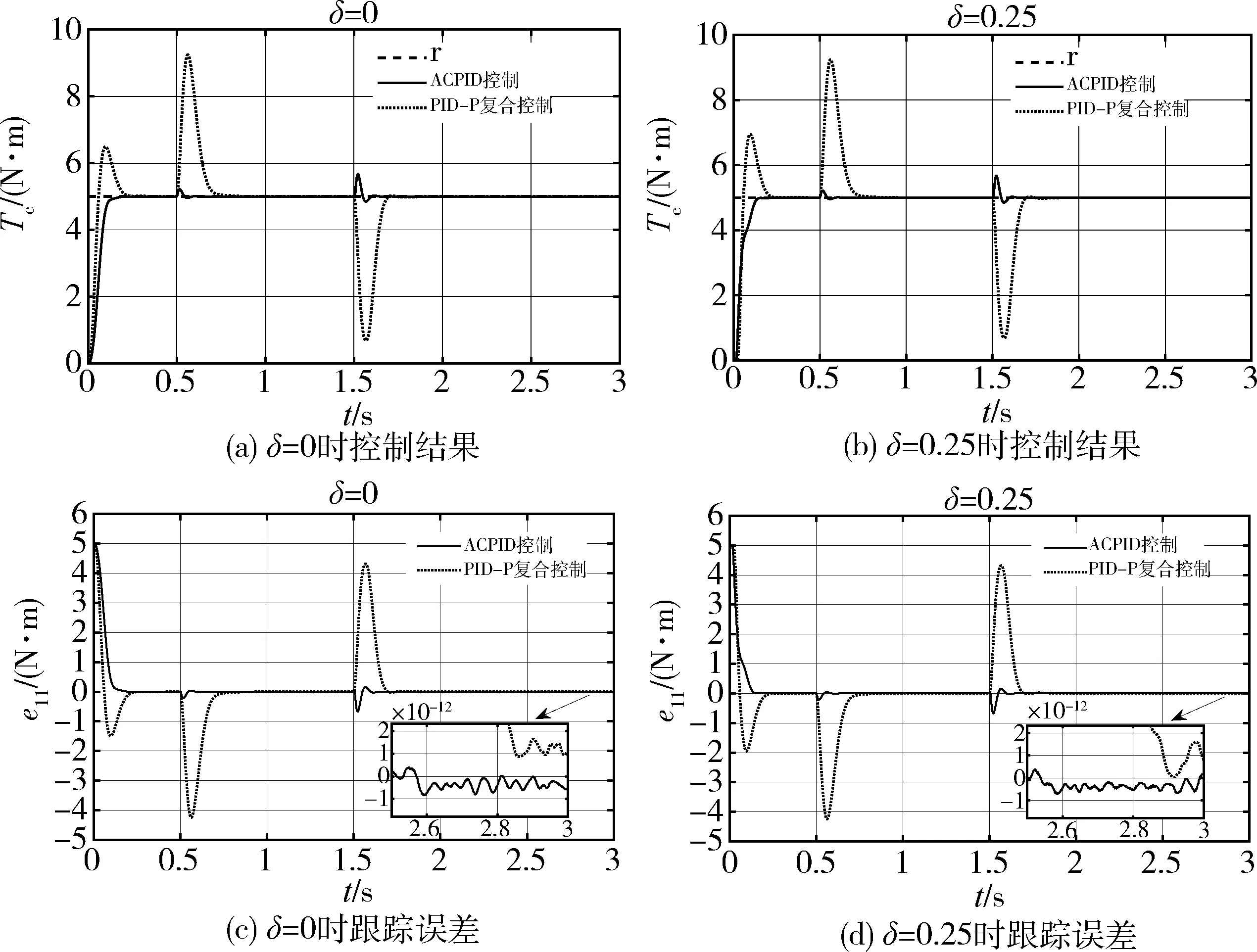
当0 由式(15)可得系统的单位冲激响应为 h11(t)=texp(-zc1t) (16) 由式(14)可得受控误差系统的时域形式为 (17) 其中,“*”表示卷积积分运算. (18) 根据式(16)可知,当0 (19) 将式(19)代入式(18),可得稳态误差为 (20) 由式(20)可知稳态误差与被控系统的具体模型无关,因此,ACPD控制系统具有良好的抗扰动鲁棒性,证毕. 定理2的证明参照定理1,此处不再赘述. 由定理1~2可知,当速度因子大于0时,ACPD和ACPID控制系统都是鲁棒稳定的,且速度因子越大,控制系统的稳态精度则越高,抗扰动能力则越强,否则反之.然而,速度因子过大,则会因比例控制力和积分控制力过大而出现超调现象,特别是在启动控制初期,由于误差较大,要求使用较小的速度因子;进入稳态过程后,由于误差较小,则要求使用较大的速度因子以便提高抗扰动能力和稳态控制精度.为此,本文设计了基于误差的自适应速度因子模型,即:当e11较大时,使zc1取较小值,否则取较大值,具体如下: (21) 同时考虑到外环的ACPD虚拟控制器为内环ACPID控制器提供虚拟期望指令,因而要求zc2与zc1之间应该满足不等式关系zc2≥2zc1,且根据仿真实验测试,当zc2=(2~5)zc1时都能实现有效控制. 为了验证本文控制方法的有效性,与传统PID控制以及文献[2]进行比较分析,被控对象的各参数与文献[2]一样,如表1所示. 表1 系统参数 传统PID控制方法的参数由Simulink自带的工具箱调节:kp=0.008 3,ki=21.425 1,kd=0.002 1;PID-P复合控制方法的参数跟文献[2]一致;本文ACPID控制方法的相关参数为tr=0.2 s,α=3,max(|e11|)=5,zc1=75exp(-0.1|e11|),y3dm=2 500,b=8.7×107,zc2=4zc1,um=100.期望轨迹r是幅值为5 N·m的阶跃信号,采样频率为1 000 Hz. 当齿隙分别为δ=0与δ=0.25时,3种控制方法的控制结果如图3所示.由图3可知,当δ=0时,由于三明治系统机械谐振的影响,传统PID控制的输出力矩一直存在振荡现象,具有较大的稳态误差,当δ=0.25时,振荡现象更加剧烈;PID-P复合控制方法可以消除三明治系统机械谐振的影响,然而其响应速度则会随齿隙的增大而明显变慢;与PID-P复合控制方法相比,ACPID控制方法的响应速度快了0.1 s,而且与齿隙没有明显关系.此外,ACPID控制方法的稳态误差小于10-12,而PID-P复合控制方法的稳态误差则小于2×10-12,表明ACPID控制方法具有更高的稳态控制精度. 图3 空载时控制结果 在实际控制过程中,负载往往会发生改变,因此本文选取的负载转矩如下所示: (22) 其中,t为仿真时间. 由于文献[2]没有考虑负载情况,为了进一步检验有负载情况下的控制效果,本文按照文献[2]的控制方法与本文控制方法做了比较实验,其控制结果如图4所示.由图4可知,无论是δ=0还是δ=0.25,在式(22)的负载情况下,本文控制结果与空载时的结果相当,而文献[2]的PID-P复合控制方法在负载突变时则会产生严重超调,其最大超调高达80%,且需要0.25s才能恢复到稳态,而本文的最大超调小于16%,且在0.125s内即可恢复到稳态,表明本文控制方法具有很强的抗负载扰动能力.此外,ACPID控制方法的稳态误差小于10-12,而PID-P复合控制方法的稳态误差则小于2×10-12,表明ACPID控制方法具有更高的稳态控制精度. 图4 带负载时控制结果 针对一类非线性且出现振荡的三明治结构挠性传动系统的控制问题,本文提出了一种基于ACPID控制理论的控制方法.该方法根据期望输出和ACPD虚拟控制器来形成虚拟指令,再由ACPID控制器对获得的虚拟指令进行跟踪控制来形成控制信号,从而实现三明治结构挠性传动系统的控制.与文献[2]相比,本文控制方法的突出优势是控制系统结构简单,仅涉及一个速度因子的镇定.仿真结果表明,在存在齿轮间隙的情况下,本文控制方法比文献[2]的响应速度提高了40%;在负载突变情况下,本文控制方法的最大超调小于16%,恢复时间约为0.125 s,而文献[2]的最大超调高达80%,且恢复时间约为0.25 s,表明本文控制方法具有很强的抗负载扰动能力.
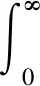

2.4 自适应速度因子

3 仿真分析

3.1 仿真实验1:空载情况下的仿真结果与分析
3.2 仿真实验2:在负载情况下的仿真结果与分析
4 结 论
